621 任务调度器
下面是题目
下面是题目给出的代码模板
1 | class Solution { |
很显然我们要把题目读透
- 假设数组 [“A”,”A”,”A”,”B”,”B”,”C”],n = 2,A的频率最高,记为count = 3,所以两个A之间必须间隔2个任务,才能满足题意并且是最短时间(两个A的间隔大于2的总时间必然不是最短),因此执行顺序为: A->X->X->A->X->X->A,这里的X表示除了A以外其他字母,或者是待命,不用关心具体是什么,反正用来填充两个A的间隔的。上面执行顺序的规律是: 有count - 1个A,其中每个A需要搭配n个X,再加上最后一个A,所以总时间为 (count - 1) * (n + 1) + 1
- 要注意可能会出现多个频率相同且都是最高的任务,比如 [“A”,”A”,”A”,”B”,”B”,”B”,”C”,”C”],所以最后会剩下一个A和一个B,因此最后要加上频率最高的不同任务的个数 maxCount
借助桶的思维,我们可以更直观的了解这题目的思路(不是我的题解!)
https://leetcode-cn.com/problems/task-scheduler/solution/tong-zi-by-popopop/ 作者:popopop
上面是原帖,我按照他的基础加上了自己的理解
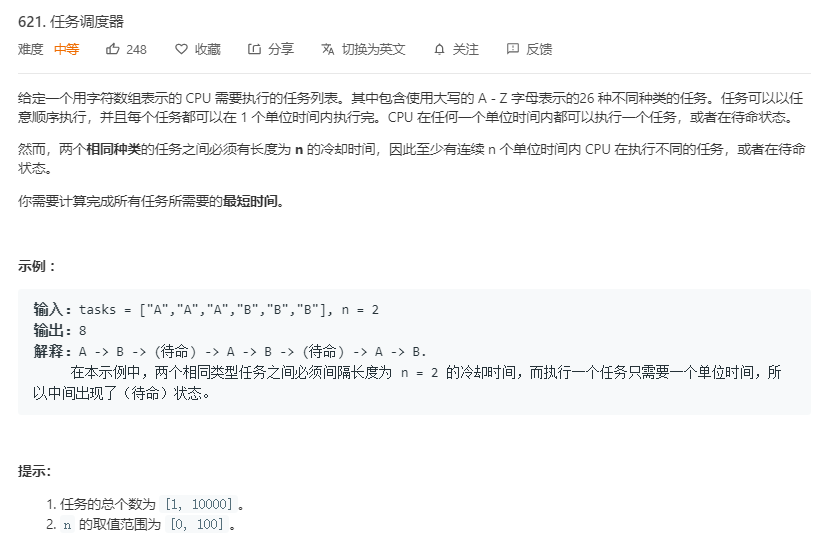
- 建立大小为n+1的桶子,个数为任务数量最多的那个任务,比如下图,等待时间n=2,A任务个数6个,我们建立6个桶子,每个容量为3:
我们可以把一个桶子看作一轮任务

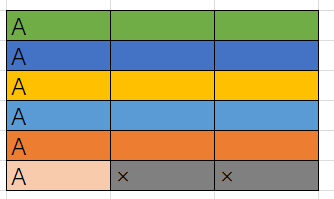
第二列、第三列的空格就是用来填剩下的任务的,这样能保证每个任务之间都间隔n个长度
但是,最后一个任务A的时间后没有了其他任务,所以完成任务A所需的时间应该是(6-1)*3+1=16
如果添加了任务的话,会怎么样呢
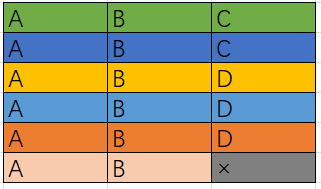
- 可以看到C其实并没有对总体时间产生影响,因为它被安排在了其他任务的冷却期间;
而B和A数量相同,这会导致最后一个桶子中,我们需要多执行一次B任务,现在我们需要的时间是(6-1)*3+2=17
前面两种情况,总结起来:总排队时间 = (桶个数 - 1) * (n + 1) + 最后一桶的任务数
- 当冷却时间不够任务的总数,那么怎么办呢?
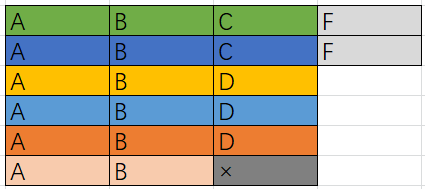
此时我们可以临时扩充某些桶子的大小,插进任务F,对比一下插入前后的任务执行情况:
插入前:ABC | ABC | ABD | ABD | ABD |AB
插入后:ABCF | ABCF | ABD | ABD | ABD |AB
我们在第一个、第二个桶子里插入了任务F,不难发现无论再继续插入多少任务,我们都可以类似处理,而且新插入元素肯定满足冷却要求
继续思考一下,这种情况下其实每个任务之间都不存在空余时间,冷却时间已经被完全填满了。
也就是说,我们执行任务所需的时间,就是任务的数量
这样按公式算出来,那么所花费的时间是17,但是因为每个任务之间已经不存在空余时间,所以这时候任务所需的时间是19,所以要返回多的
所以,当任务之间存在空闲时间的时候,肯定是公式算出来的时间多,但是当任务之间没有空暇时间,那么任务的数量>=公式的结果
1 | class Solution { |