链式前向星
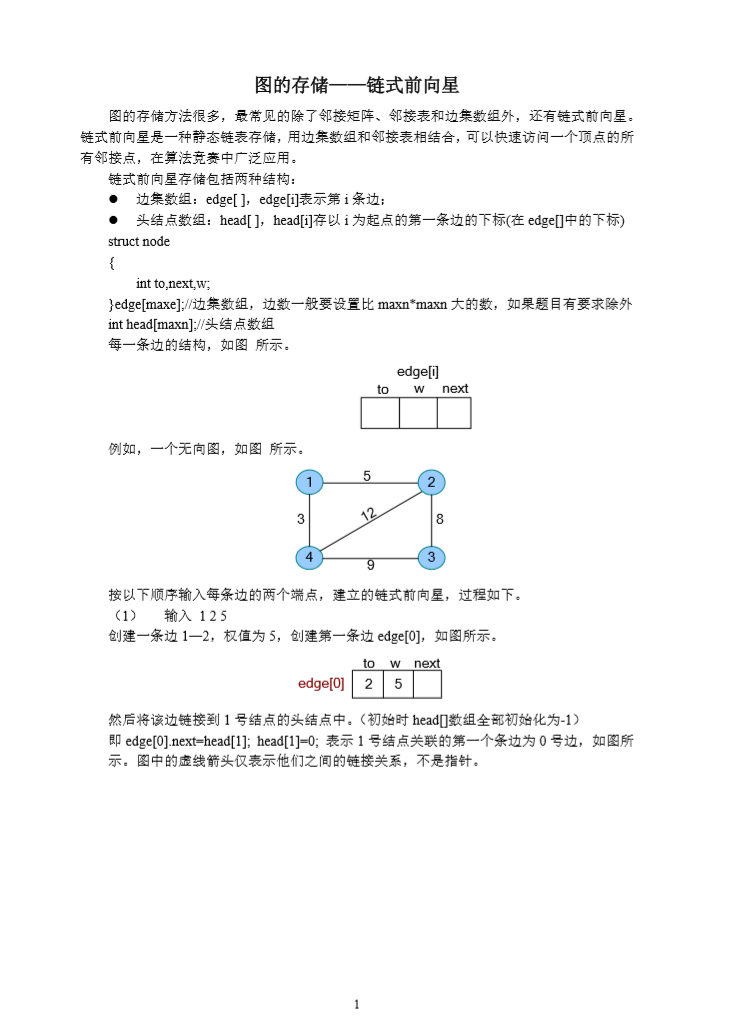
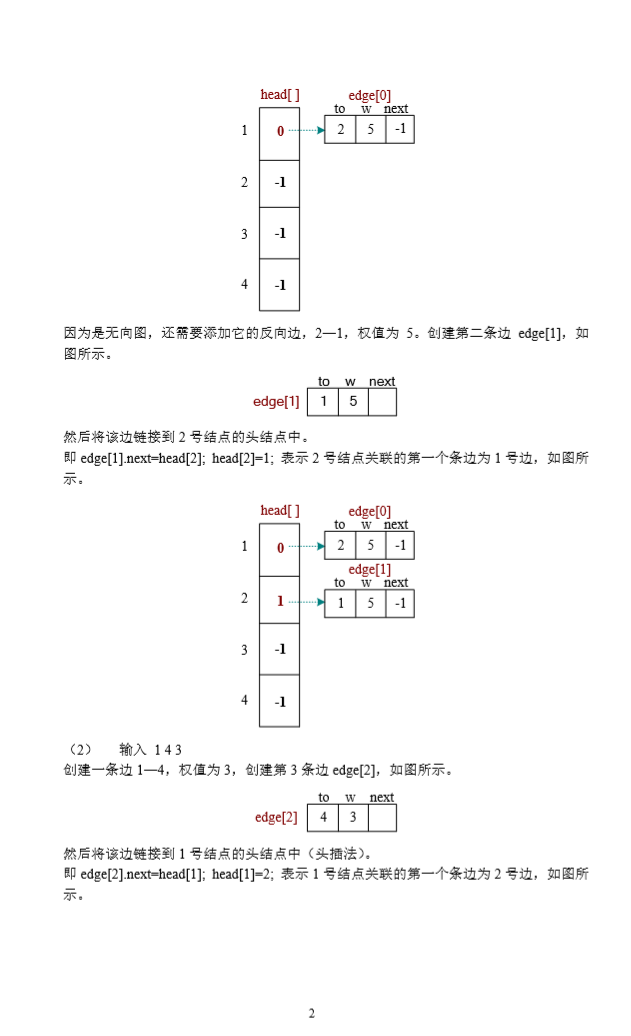
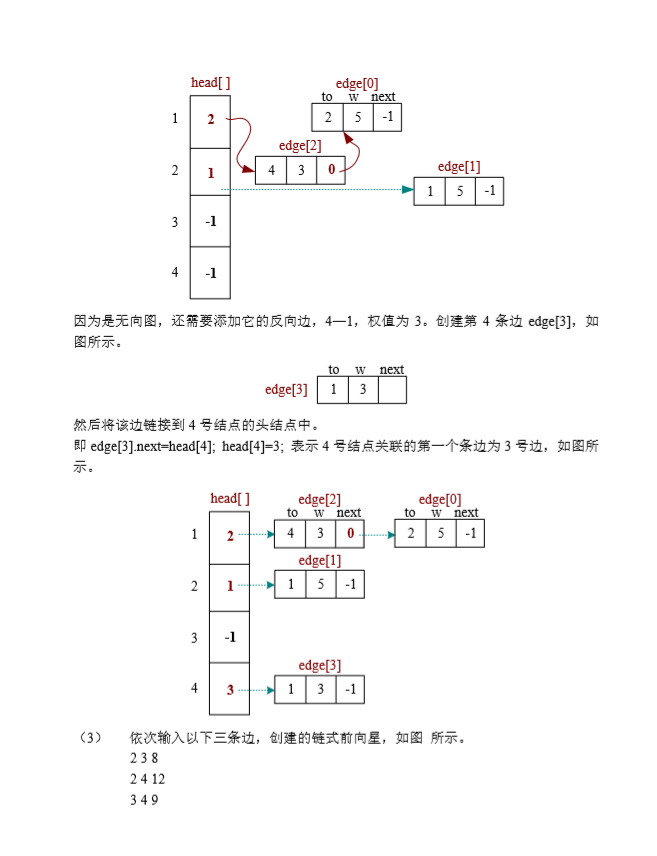
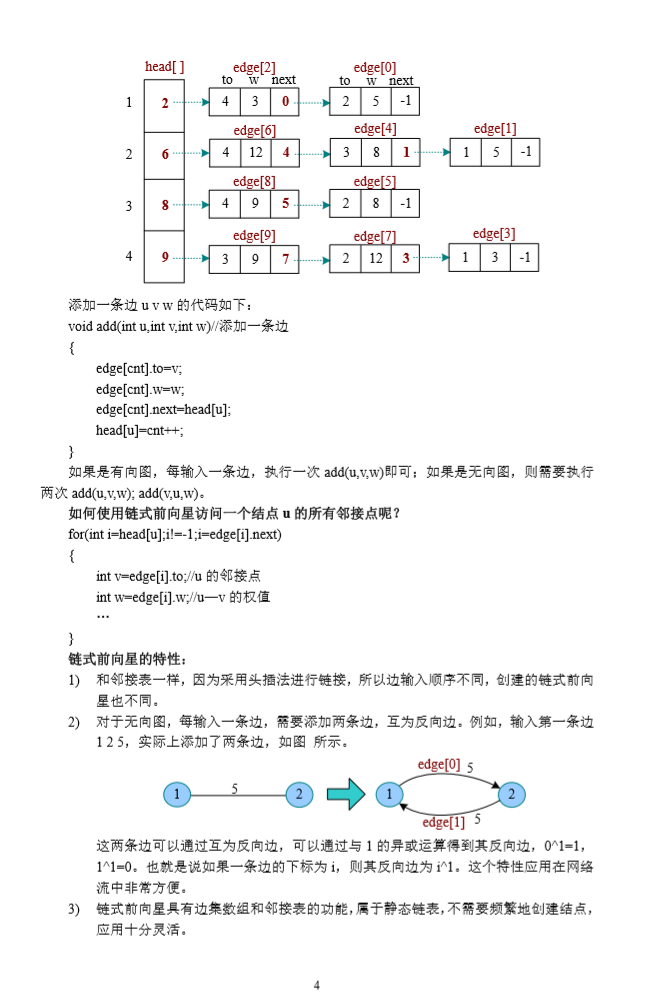
- 链式前向星在存储图时十分有用,特别是当边有权值时。我们用过一道题目了来具体分析一下
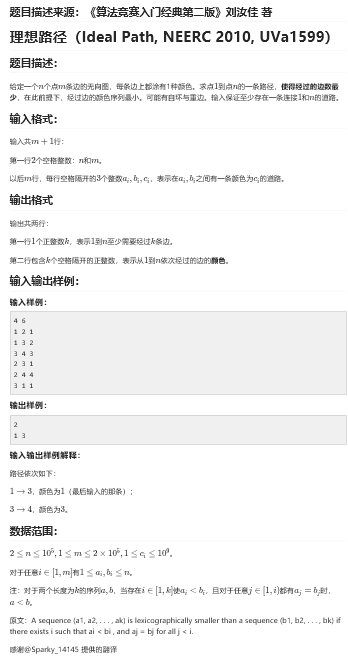
链式前向星只是一种应用,是一种小技巧。所以我们先要构造一个链式前向星来存储数据。
1 | int n,m,cnt;//全局变量默认为0 |
- 构建好,并存储好后,开始bfs
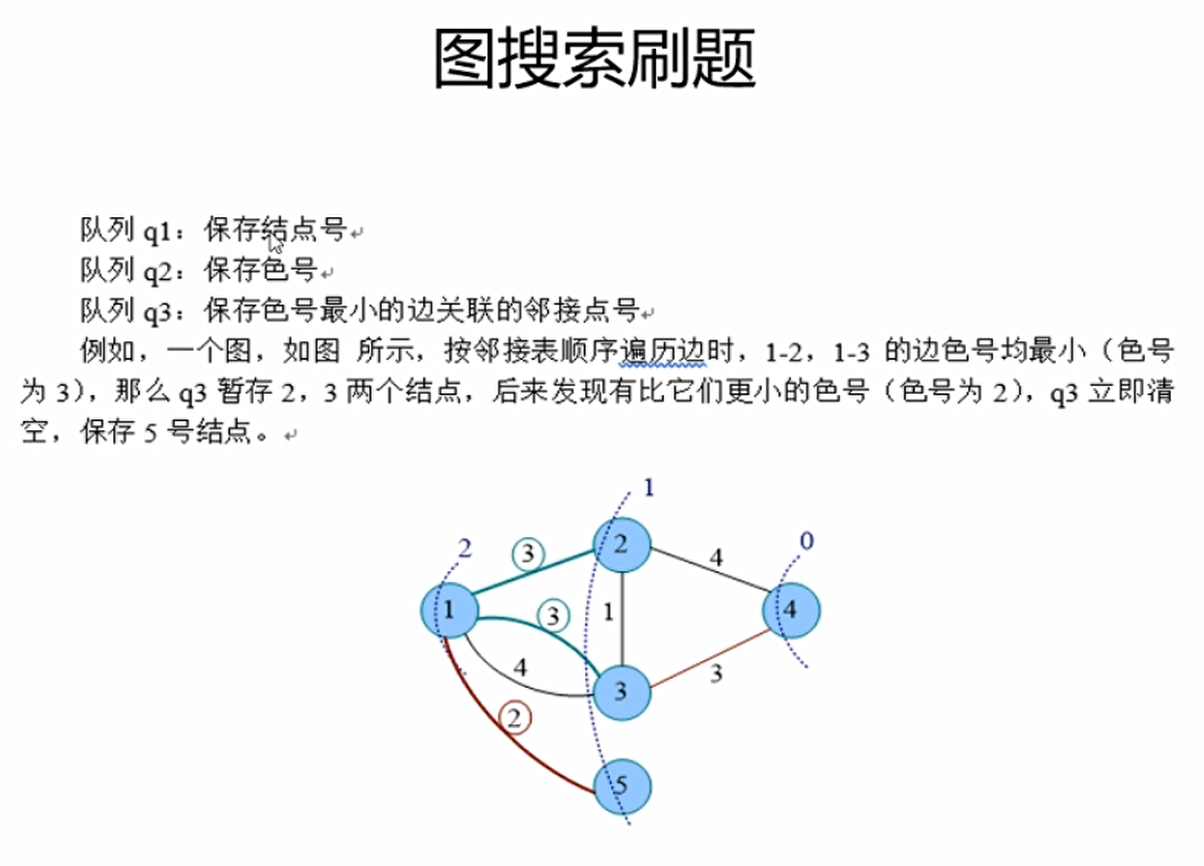
1 | //关于为什么要逆向标高 |
- 反向遍历之后,我们需要从1开始正向遍历
1 | void bfs2() |





链式前向星只是一种应用,是一种小技巧。所以我们先要构造一个链式前向星来存储数据。
1 | int n,m,cnt;//全局变量默认为0 |

1 | //关于为什么要逆向标高 |
1 | void bfs2() |