背包问题

Posted on | In
Words count in article: 4.9k | Reading time ≈ 21

下面是问题

背包问题是动态规划的经典问题之一。是指在一个有容积或重量限制的背包中放入物品，物品有体积、重量、价值等属性。要求在满足背包限制的情况下，如何放置物品，让背包中的物品价值之和最大。根据物品限制条件的不同，可分为01背包，完全背包，多重背包和分组背包等。

如果每个物品都有无数个，那么就是完全背包

如果每个物品都只有1个，要么放进去，要么不放进去，那么就是01背包

如果每个物品都有数量，但数量都是有限的，那么就是多重背包

如果把物品分组，每组只能选一个，那么就是分组背包

01背包

问题描述

给定n个物品，每个物品有重量$w_i$和价值$v_i$,每种物品有且只有一个。背包容量为W，要求在不超过背包容量的情况下，如何放置物品，让背包中物品的价值之和最大

假设第i阶段表示处理第i个物品，第i-1阶段表示处理第i-1个物品。当处理第i个物品时，前i-1个物品已处理完毕。只需要考虑第i-1阶段向第i阶段转义.

用$c[i][j]$表示前i件物品放入一个容量为j的背包可以获得的最大价值

对于第i个物品的处理状态：

示例

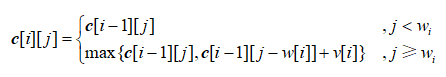
  • 那么当我们的背包容量都不能够放下当前的物品的时候，那么直接照抄上一阶段的价值

  • 那么如果能放得下的话，那么还需要做比较到底要不要放入的问题

    • 那么如果不放入，那么还是照抄上一个阶段的价值
    • 如果放入的话，那么就这样考虑：放入了以后，i的数量加了1，而背包中物体的总重量增加了$w_i$ ，所以，只要考虑$c[i-1][j-w[i]]$这一格的价值，再加上 我们加进去的物体的价值，就得到了我们新的价值。
    • 如果这个物体很重但是价值不高，那应该是是不放价值高
1
2
3
4
5
6
7
8
9
10
for(i = 1,i<=n,i++)
{
	for(j = 1,j<=w,j++)
	{
		if(j<w[i])	//当物品的重量大于背包的容量，则不放这个物品
			c[i][j] = c[i-1][j];
		else		//否则比较次物品放于不放是否能使背包内的价值最大
			c[i][j] = max(c[i-1][j],c[i-1][j-w[i]]+v[i]);
	}
}

算法分析：

时间复杂度：算法中有主要的两层嵌套的for循环，时间复杂度为$O(n*w)$

空间复杂度：算法中有二维数组$c[n][w]$，所以空间复杂度为$O(n*w)$

源码一览：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
#define maxn 10005
#define M 105
int c[M][maxn];//c[i][j]表示前i个物品放入容量为j背包获得的最大价值
int w[M],v[M];//w[i]表示第i个物品的重量，v[i]表示第i个物品的价值
int x[M];  //x[i]表示第i个物品是否放入背包
int main()
{
    int n,W;//n表示n个物品，W表示背包的容量
    cout<<"请输入物品的个数 n:";
    cin>>n;
    cout<<"请输入背包的容量W:";
    cin>>W;
    cout<<"请依次输入每个物品的重量w和价值v，用空格分开:";
    for(int i=1;i<=n;i++)
        cin>>w[i]>>v[i];
    for(int i=1;i<=n;i++)//初始化第0列为0
        c[i][0]=0;
    for(int j=1;j<=W;j++)//初始化第0行为0
        c[0][j]=0;
	for(int i=1;i<=n;i++)//计算c[i][j]
		for(int j=1;j<=W;j++)
			if(j<w[i])  //当物品的重量大于背包的容量，则不放此物品
				c[i][j]=c[i-1][j];
            else    //否则比较此物品放与不放是否能使得背包内的价值最大
				c[i][j]=max(c[i-1][j],c[i-1][j-w[i]]+v[i]);
	cout<<"装入背包的最大价值为:"<<c[n][W]<<endl;

    //用于测试
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=W;j++)
          cout<<c[i][j]<<"\t" ;
        cout<<endl;
    }
    cout<<endl;

    //逆向构造最优解
    int j=W;
    for(int i=n;i>0;i--)
        if(c[i][j]>c[i-1][j])
        {
            x[i]=1;
            j-=w[i];
        }
        else
            x[i]=0;
    cout<<"装入背包的物品序号为:";
    for(int i=1;i<=n;i++)
        if(x[i]==1)
           cout<<i<<"  ";
    return 0;
}

逆向构造最优解的图解

示例

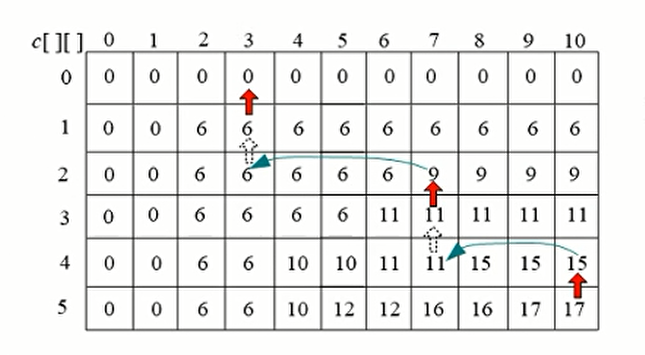
最大价值是17，那么我们先$C[5][10]$和$C[4][10]$相比，17>15 那么X[5]=1,j=j-w[i]=10-3=7

$C[4][7]$和$C[3][7]$比较，相等，说明第四个物品没有放进去

$C[3][7]$和$C[2][7]$比较，11>9，说明X[3]=1,j=j-w[i]=7-4=3

$C[2][3]$和$C[1][3]$比较，相等，说明第二个物品没有放进去

$C[1][3]$和$C[0][3]$比较，6>0，说明X[1]=1,比较结束

所以输出的时候，从1开始到n输出，放入次序为：1号，3号，5号

算法优化：

如果碰到背包数值w太大了，但是n又比较小的时候，从1开始遍历就需要很长时间

如果w过于大，那么就考虑回溯法，用一维数组求解。

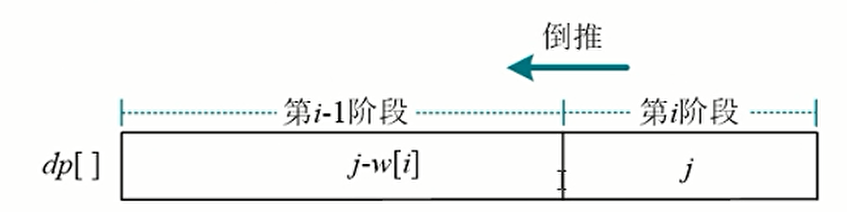
既然只需要当前列和前面列值，那么只用一个一维数组倒推就可以了

用dp[j]表示物品放入容量为j的背包可以获得的最大价值

倒退时，因为从后往前推，前面的值还未更新，仍然未第i-1阶段的结果，意味着总是用第i-1段向第i阶段进行状态转移。第i-1阶段的结果，不包括第i个物品，这样保证第i个物品最多只会放入背包一次

如果是倒推保证第i个物品最多只会放入背包一次

示例

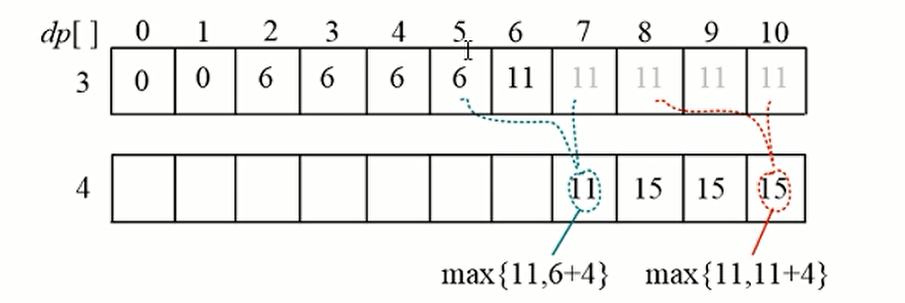
如果是正推，那么我们看到他是拿了一个更新值去和原来的方法相比。4这一个数值加了两次

示例

示例

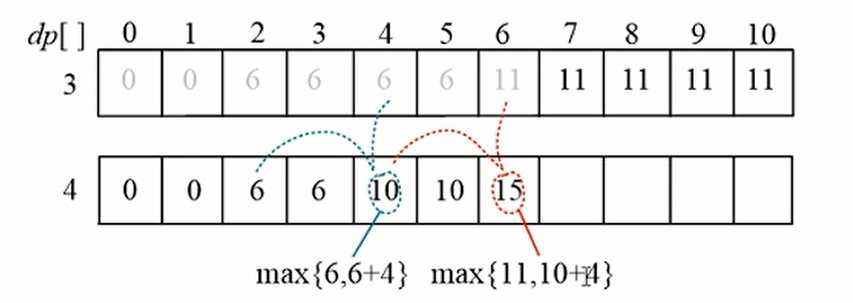
算法分析：

时间复杂度：算法中有主要的是两层嵌套的for循环，其时间复杂度是$O(n*w)$

空间复杂度：算法中使用了一维数组$dp[w]$，其时间复杂度是$O(n*w)$

1
2
3
4
5
6
7
8
9
10
void opt2(int n ,int w)
{
	for(int i;i<n;i++)
	{
		for(j = w;j>=w[i];j--)
		{
			dp[j] = max(dp[j],dp[j-w[i]]+v[i]);
		}
	}
}

源码一览：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include<iostream>
#include<cstring>
using namespace std;
#define maxn 10005
#define M 105
int dp[maxn];//dp[j]表示当前已放入容量为j的背包获得的最大价值
int w[M],v[M];//w[i]表示第i个物品的重量，v[i]表示第i个物品的价值
int x[M];  //x[i]表示第i个物品是否放入背包
int n,W;//n表示n个物品，W表示背包的容量
void opt1(int n,int W)
{
    for(int i=1;i<=n;i++)
        for(int j=W;j>0;j--)
			if(j>=w[i])//当物品的重量大于背包的容量，比较此物品放与不放是否能使得背包内的价值最大
				dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}

void opt2(int n,int W)//01背包优化一维数组 
{
	for(int i=1;i<=n;i++)
		for(int j=W;j>=w[i];j--)//逆向循环（倒推）
			dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}

void opt3(int n,int W)
{
	int sum[n];//sum[i]表示从1...i的物品重量之和
	sum[0]=0;
	for(int i=1;i<=n;i++)
		sum[i]=sum[i-1]+w[i];
	for(int i=1;i<=n;i++)
	{
        int bound=max(w[i],W-(sum[n]-sum[i-1]));//w[i]与剩余容量取最大值,sum[n]-sum[i-1]表示从i...n的物品重量之和
        for(int j=W;j>=bound;j--)
            //当物品的重量大于背包的容量，比较此物品放与不放是否能使得背包内的价值最大
           dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
	}
}

int main()
{
    cout<<"请输入物品的个数 n:";
    cin>>n;
    cout<<"请输入背包的容量W:";
    cin>>W;
    cout<<"请依次输入每个物品的重量w和价值v,用空格分开:";
    for(int i=1;i<=n;i++)
        cin>>w[i]>>v[i];
    for(int j=1;j<=W;j++)//初始化第0行为0
        dp[j]=0;
    opt1(n,W);
    //opt2(n,W);
    //opt3(n,W);
    cout<<"装入背包的最大价值为:"<<dp[W]<<endl;

    //测试dp[]数组结果
    for(int j=1;j<=W;j++)
        cout<<dp[j]<<"  ";
    cout<<endl;

    return 0;
}

完全背包：

问题描述:

给定n个物品，每个物品有重量$w_i$和$v_i$ ，每种物品的数量没有限制。背包容量为W，要求在不超过背包容量的情况下，如何放置物品，让背包中的价值之和最大。可以对每个物品依次检查是否放入或者不放入，对第i个物品的处理状态：

用$c[i][j]$表示前i件物品放入一个容量为j的背包，可以获得的最大价值

  • 如果尚未放入第i个物品，装入背包的价值不增加。那么问题就转化为’’前i-1件物品放入容量为j的背包中’’，最大值为$c[i-1][j]$
  • 如果从第i件物品选择一个放入，因为第i件物品可以多次放入，相当于从第i-1阶段向第i阶段转化。问题就转化为“ 前i-1件物品放入容量为j-w[i]的背包中”，此时获得的最大价值就是$c[i][j-w[i]]$,再加上放入第i件物品获得的价值v[i].即$c[i][j-w[i]]+v[i]$

也可以优化为一维数组dp[j]，然后采用正向循环，这样保证每个物品可以放入多次，用dp[j]表示物品放入一个容量为j的背包可以获得的最大价值

完全背包问题每种物品有无限个，可以多次放入，因此采用正推的形式求解。只需要讲01背包的代码的第二个for语句改成从前向后正向循环即可。、

1
2
3
4
5
6
void comp_knapsack(int n ,int w)
{
	for(int i = 1;i<=n;i++)
		for(j = w[i];j<=W;j++)
			dp[j] = max(dp[j],dp[j-w[i]]+v[i]);
}

代码一览

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include<iostream>
#include<cstring>
using namespace std;
#define maxn 10005
#define M 105
int dp[maxn];//dp[j]表示当前已放入容量为j的背包获得的最大价值
int w[M],v[M];//w[i]表示第i个物品的重量，v[i]表示第i个物品的价值
int n,W;//n表示n个物品，W表示背包的容量

void comp_knapsack(int n,int W)//完全背包 
{
    for(int i=1;i<=n;i++)
		for(int j=w[i];j<=W;j++)//正序循环（正推）
			dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}

int main()
{
    cout<<"请输入物品的个数 n:";
    cin>>n;
    cout<<"请输入背包的容量W:";
    cin>>W;
    cout<<"请依次输入每个物品的重量w和价值v,用空格分开:";
    for(int i=1;i<=n;i++)
        cin>>w[i]>>v[i];
    for(int j=1;j<=W;j++)//初始化第0行为0
        dp[j]=0;
    comp_knapsack(n,W);
    cout<<"装入背包的最大价值为:"<<dp[W]<<endl;
    //测试dp[]数组结果
    for(int j=1;j<=W;j++)
        cout<<dp[j]<<"  ";
    cout<<endl;
    return 0;
}

多重背包

问题描述：

​ 给定n个物品，每个物品中有重量$w_i$和价值$v_i$,每种物品的数量可以大于1但是有限制，第i个物品有$c_i$个，背包容量为W，要求在不超过背包容量的情况下，如何放置物品，让背包中物品的价值之和最大

1.暴力拆分

​ 暴力拆分就是把第i种物品看作是$c_i$个独立的物品，每个物品只有一个，转化为01背包问题。但这样很容易超时

2.二进制拆分

​ 当物品满足c[i]*w[i]>=W时，可以认为这种物品时不限数量的，按照完全背包的求解方法即可，否则，可以采用二进制拆分，把c[i]个物品拆分成若干物品怎么拆分呢？

首先$2^0+2^1+2^2…2^p<=C_i$找到这个p，然后把$C_i$分解成$2^0, 2^1,..2^p,C_i-(2^0, 2^1,..2^p)$一共p+2个，如果刚刚好等于的话那就是p+1个

比如说 $c_i = 9$那么也就是说分成1，2，4，2，四个物体，这样我们其实可以在这四个里取1-9中的任何数字，达到了拆分的效果

3.数组优化

用一个$num[j]$数组记录容量为j时，放入了多少个第 $i$ 个物品，由此实现数量限制约束

代码一览

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include<iostream>
#include<cstring>
using namespace std;
#define maxn 10005
#define M 105
int dp[maxn],num[maxn];//dp[j]表示当前已放入容量为j的背包获得的最大价值,num[j]统计数量 
int w[M],v[M],c[M];//w[i]表示第i个物品的重量，v[i]表示第i个物品的价值,c[i]表示第i个物品的数量 
int n,W;//n表示n个物品，W表示背包的容量

void multi_knapsack1(int n,int W)//暴力拆分 超时！！！ 
{
    for(int i=1;i<=n;i++)
    	for(int k=1;k<=c[i];k++)//多一层循环 
			for(int j=W;j>=w[i];j--)
				dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}

void multi_knapsack2(int n,int W)//二进制拆分 
{
    for(int i=1;i<=n;i++)
    {
		if(c[i]*w[i]>=W)//转化完全背包 
        {
            for(int j=w[i];j<=W;j++)
                dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
        }
        else
        {
            for(int k=1;c[i]>0;k<<=1)//二进制拆分 k<<=1就等于k=k*2
        	{
	            int x=min(k,c[i]);
	            for(int j=W;j>=w[i]*x;j--)//转化01背包 
	                dp[j]=max(dp[j],dp[j-w[i]*x]+x*v[i]);
	            c[i]-=x;
        	} 
    	}
	}
}
                                            
void multi_knapsack3(int n,int W)//数组优化 ,完全背包+数量限制
{
	for(int i=1;i<=n;i++)
    {
        memset(num,0,sizeof(num));//统计数量 ,记录第i个物品用了多少个
        for(int j=w[i];j<=W;j++)
        {
            if(dp[j]<dp[j-w[i]]+v[i]&&num[j-w[i]]<c[i])//首先判断数量是不是小于c[i]
            {
                dp[j]=dp[j-w[i]]+v[i];
                num[j]=num[j-w[i]]+1;
            }
        }
    }
}

int main()
{
    cout<<"请输入物品的个数 n:";
    cin>>n;
    cout<<"请输入背包的容量W:";
    cin>>W;
    cout<<"请依次输入每个物品的重量w、价值v和数量c,用空格分开:";
    for(int i=1;i<=n;i++)
        cin>>w[i]>>v[i]>>c[i];
    for(int j=1;j<=W;j++)//初始化第0行为0
        dp[j]=0;
    multi_knapsack1(n,W);
    cout<<"装入背包的最大价值为:"<<dp[W]<<endl;
    //测试dp[]数组结果
    for(int j=1;j<=W;j++)
        cout<<dp[j]<<"  ";
    cout<<endl;
    return 0;
}

分组背包

问题描述

给定n组物品，第i组有ci 个物品，第i组第j个物品有重量$w{ij}$和价值$v_{ij}$，背包容量为W，要求再不超过背包容量的情况下，每组至多选择一个物品，如何放置物品，让背包中物品价值之和最大。

因为每组之多选择一个物品，可以将每组看作一个整体，然后转换成01背包

算法分析：

用$C[i][j]$ 表示前i组物品放入一个容量为j的背包可以获得的最大价值，对于第i组物品的处理状态：

  • 不放入第i组的物品，装入背包的价值不增加。那么问题就转化为“前i-1组物品放入容量为j的背包当中”，最大价值时$C[i][j]$
  • 放入第i组的第k个物品，相当于从第i-1阶段向第i阶段转化。问题就转化为“前i-1组物品放入容量为$j-[i][k]$ 的背包中“，此时获得的最大价值就是$c[i-1][j-w[i][k]]+v[i][k]$

需要注意的是，枚举组内各物品的k一定在最内层循环，如果放在j的外层，那么则变为多重背包的暴力拆分算法，因为枚举放在j的外层.会出现组内多个物品多个放入的情况，这样就变成了多重背包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include<iostream>
#include<cstring>
using namespace std;
#define maxn 10005
#define M 105
int dp[maxn];//dp[j]表示当前已放入容量为j的背包获得的最大价值 
int w[M][M],v[M][M],c[M];//w[i][j]表示第i组第j个物品的重量，v[i][j]表示第i组第j个物品的价值,c[i]表示第i组物品的数量 
int n,W;//n表示n组物品，W表示背包的容量

void group_knapsack(int n,int W)//分组背包
{
    for(int i=1;i<=n;i++)
		for(int j=W;j>=0;j--) 
			for(int k=1;k<=c[i];k++)//枚举组内各个物品
				if(j>=w[i][k])
					dp[j]=max(dp[j],dp[j-w[i][k]]+v[i][k]);
    //最内层的k循环，仅仅是穷举了一个最大值，然后实现更新，dp[j]只更新了一次
}

int main()
{
    cout<<"请输入物品的组数 n:";
    cin>>n;
    cout<<"请输入背包的容量W:";
    cin>>W;
    cout<<"请依次输入每组物品的数量,每组物品的重量和价值：";
    for(int i=1;i<=n;i++)
    { 
        cin>>c[i];
		for(int j=1;j<=c[i];j++)
			cin>>w[i][j]>>v[i][j];
	} 
    for(int j=1;j<=W;j++)//初始化第0行为0
        dp[j]=0;
    group_knapsack(n,W);
    cout<<"装入背包的最大价值为:"<<dp[W]<<endl;
    //测试dp[]数组结果
    for(int j=1;j<=W;j++)
        cout<<dp[j]<<"  ";
    cout<<endl;
    return 0;
}

现在就可用动态规划的方法运用上面的公式来填表求解了.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <iostream>
#include <vector>
using namespace std;
int main ()
{
    //这里把值和重量分开存储了
    vector<int> value;
    vector<int> weight;
    vector<int> DP;
    int Number,maxSize;
    //Nis the number of items ,V is your capacity
    while ( cin >> Number >> maxSize )
    {
        if(Number<0&&maxSize<0)
            break;
        value.resize(Number+1);
        weight.resize(maxSize+1);
        DP.clear();
        DP.resize(maxSize+1);
        for ( int i = 1; i <= Number; i++ )
        {
            cin >> weight[i] >> value[i];
        }
        for ( int v = 1; v <= maxSize; v++ )
        {
            printf("%3d",v);
        }
        cout<<endl;
        for ( int i = 1; i <= Number; i++ )//row
        {
            for ( int v = 1; v <= maxSize; v++ )//column
            {
//这里的设计很巧妙，因为现在DP数组都是上一层的值，如果有需要改动的地方，就改动，否则保持原样
				//第1层的dp初始化都是0
                if ( v >= weight[i] )
                {
                    if ( DP[v-weight[i]] + value[i] >= DP[v] )
                    {
                        DP[v] = DP[v-weight[i]] + value[i];
                    }
                }
                printf("%3d",DP[v]);
            }
            cout<<endl;
        }
        cout << DP[maxSize] << endl;
    }
    return 0;
}

示例

示例

-------------本文结束，感谢您的阅读-------------