重积分
写在前面
- 终于等到这一天了,想到几天之后就要quiz的我头皮发麻
- 本来的笔记再oneNote上,但都是图片之类的。。煞是难看
- 只保存一些图片根本起不到学习的效果
- 算了,还是手敲公式⑧
- 五一结束希望能够写完,只写最重要的公式和例子,废话少说
二重积分的计算
利用直角坐标计算二重积分
当被积函数$f(x,y)\geq0$且在D上连续时,若D为X型区域
$ D:\left{ \begin{aligned} \varphi_1(x)\leq y\leq \varphi_2(x)\a\leq x\leq b \end{aligned} \right. $

则
$\iintD f(x,y)dxdy = \int_a^bdx \int{\varphi_1(x)}^{\varphi_2(x)}f(x,y)dy$
若D 为Y-形区域
则
$\iintD f(x,y)dxdy = \int_c^ddy \int{\psi_1(x)}^{\psi_2(x)}f(x,y)dx$\
利用极坐标计算二重积分
用 $ x = rcos\theta和y =r\sin\theta$ 带入原方程
则
$\iintD f(rcos\theta,rsin\theta)rdrd\theta = \int\alpha^\beta d\theta \int_{\varphi_1(\theta)}^{\varphi_2(\theta)}f(rcos\theta,rsin\theta)rdr$
特别的,对D:
$\iint_D f(rcos\theta,rsin\theta)rdrd\theta = \int_0^{2\pi} d\theta \int_0^{\varphi(\theta)}f(rcos\theta,rsin\theta)rdr$
交换积分次序
- 有些积分是超越函数,并没有对应的原函数 。这是交换积分次序显得额外重要!
$\int1^3dx\int{x-1}^2 \sin y^2 dy$
交换机分次序的方法:先画出积分域,然后根据区域的形状来交换.有时交换积分域后编程了分段积分。这时候就更加依赖画图了。
交换 $\int0^\pi dx\int{-sin\frac{x}{2}}^{sinx}f(x,y)dy$ 的积分区域
画图得出区域需要分为 $D_1\cup D_2$,其中
$D_1 = {(x,y)|arcsin(y)\leq x\leq\pi-arcsin(y),0\leq y\leq 1}$
$D_2 = {(x,y)|-2arcsin(y)\leq x\leq\pi,-1\leq y\leq 0}$
所以 原式:$\int{0}^1dy\int{arcsin(y)}^{\pi-arcsin(y)}f(x,y)dx+\int{-1}^0dy\int{-2arcsin(y)}^\pi f(x,y)dx$
别忘了代换

二重积分对称性的重要结论
- 若D关于y轴对称,那么
1) 当f(x,y) 在D上为x的奇函数,有 $I = 0$ ;
2) 当f(x,y) 在D上为x的偶函数,则有 $I = 2\iint_{D_1}f(x,y)d\sigma$, - 若D关于x轴对称,那么
1) 当f(x,y) 在D上为x的奇函数,有 $I = 0$ ;
2) 当f(x,y) 在D上为x的偶函数,则有 $I = 2\iint_{D_1}f(x,y)d\sigma$,
所以在展开的时候,我们先要把能化成0 的全部化成0,比如对于D为一个以原点为圆心的圆的时候,$\iint{\Sigma} (x+y-2)^2dS$ , 我们就可以先把其展开成$\iint\Sigma (x^2+y^2+4-4x-4y+2xy)~dS$ ,因为D关于x轴,y轴都对称。而 -4x,-4y,2xy都是关于x或y的基函数,所以他们的积分都是0,原式就可以简化为 $\iint_\Sigma(x^2+y^2+4)dS$
课本解答
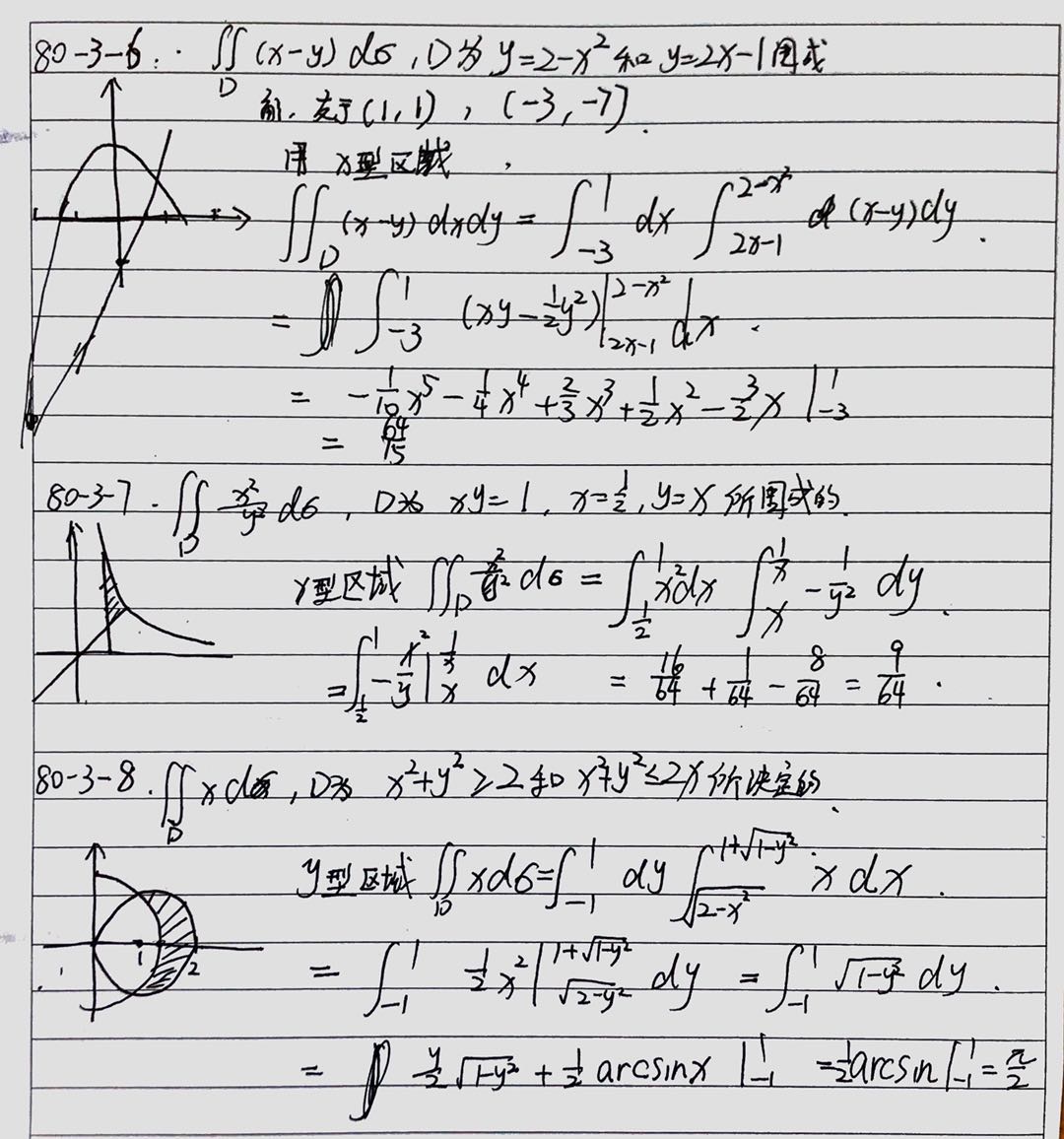



三重积分的计算
- 先看看概念吧

利用直角坐标计算三重积分
投影法(“先1后2”)
$\Omega:\left{ \begin{aligned} z_1(x.y)\leq r\leq z_2(x,y)\0\leq \theta\leq 2\pi \end{aligned} \right.$
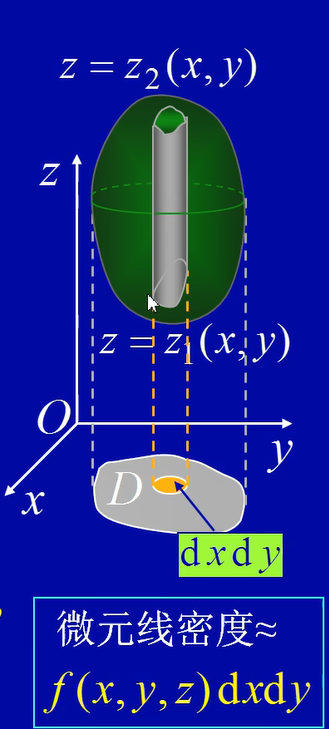
那么细长柱体微元的质量为
$(\int_{z_1(z,y)}^{z_2(x,y)}f(x,y,z)dz)dxdy$
该物体的质量就是:
$\iiint\Omega f(x,y,z)dv = \iint_D(\int{z_1(z,y)}^{z_2(x,y)}f(x,y,z)dz)dxdy$
就等于
$\iintDdxdy\int{z_1(z,y)}^{z_2(x,y)}f(x,y,z)dz$
截面法(“先2后1”)
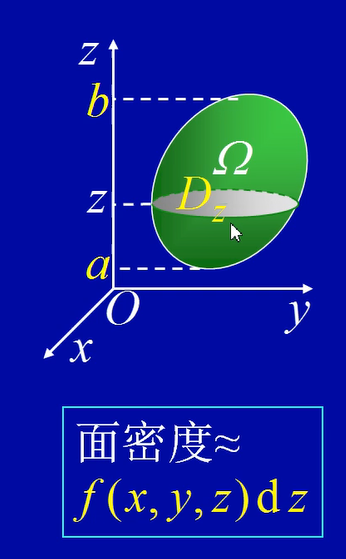
$\Omega:\left{ \begin{aligned}(x,y)\in D_z\0\leq \theta\leq 2\pi \end{aligned} \right.$
以$D_z $为底,dz为高的柱形薄片的质量为
$(\iint_{D_z}f(x,y,z)dxdy)dz$
那么该物体的质量就是
$\inta^b(\iint{Dz}f(x,y,z)dxdy)dz = \int_a^bdz\iint{D_z}f(x,y,z)dxdy$
三次积分法
区域 $\Omega:\left{ \begin{aligned} z_1(x.y)\leq z\leq z_2(x,y)\D:\left{ \begin{aligned}y_1(x)\leq y \leq y_2(x)\a\leq x\leq b \end{aligned} \right. \end{aligned} \right.$
利用投影法结果,把二重积分转化成二次积分得
$\iiint\Omega f(x,y,z)dv = \int_a^bdx\int{y1(x)}^{y_2(x)}dy\int{z_1(x,y)}^{z_2(x,y)}f(x,y,z)dz$
小结

如果已经知道区域在平面上的投影,那么先一后二或者先二后一的方法更加方便。
比如求上下分别为球面$x^2+y^2+z^2=2$ 和抛物面 $z=x^2+y^2$ 所围的立体的体积。我们就可以用 $V=\iint dxdy\int_{x^2+y^2}^{\sqrt{2-x^2-y^2}}dz $
利用柱坐标计算三重积分
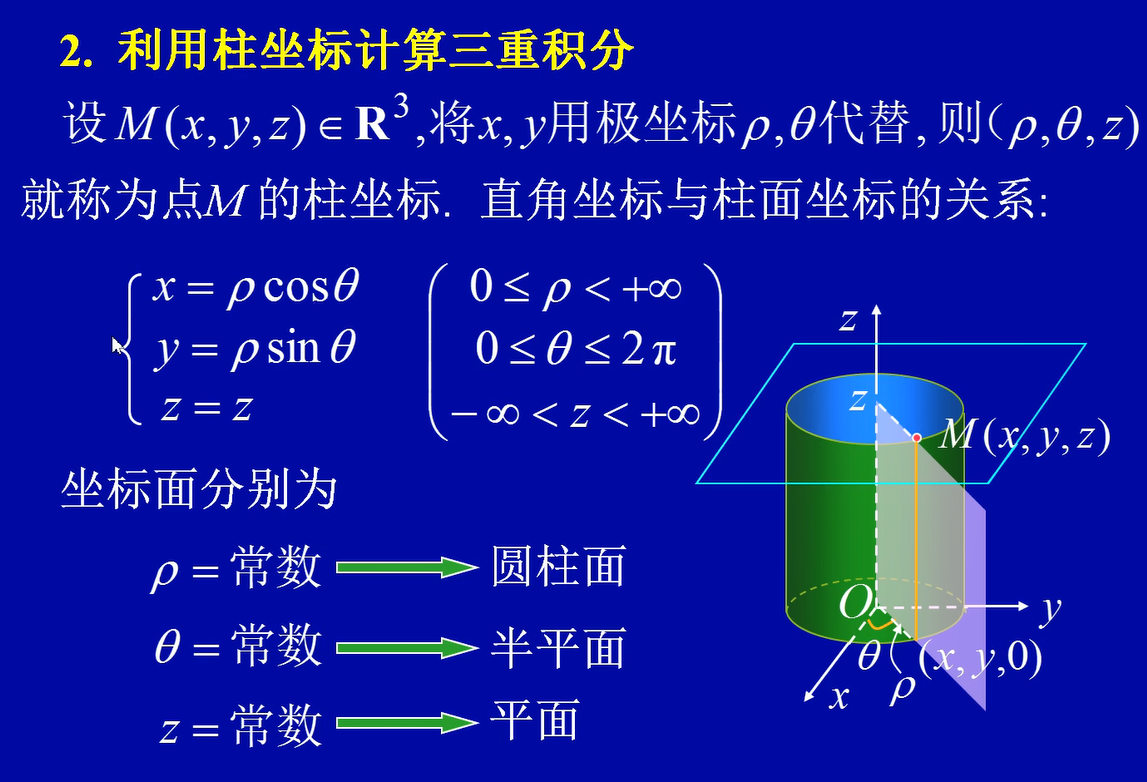
在柱面坐标系中得体积元素为
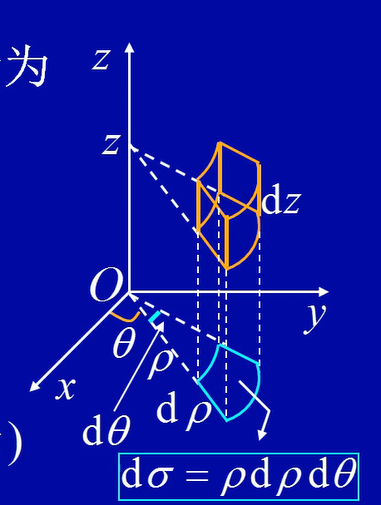
$dv = \rho d\rho d\theta dz $
因此 $\iiint\Omega f(x,y,z)dxdydz =\iiint\Omega F(\rho,\theta,z)\rho d\rho d\theta dz$
$\theta$摆在前,r摆中间, z 摆最后面
其中,$F(\rho,\theta,z)=f(\rho cos\theta ,\rho sin\theta,z)$
适用范围
- 积分域表面用柱面坐标表示时方程简单
- 被积函数用柱面坐标表示时变量相互分离
利用球坐标计算三重积分

如图所示,在球面坐标系中的体积元素为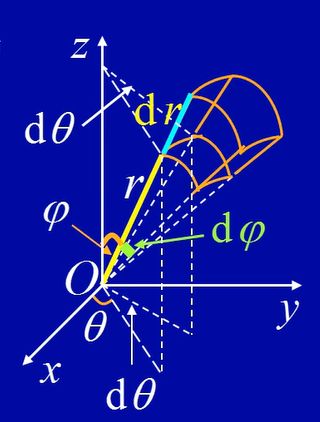
$dv = r^2 sin\varphi dr d\varphi d\theta$
因此有 $\iiint\Omega f(x,y,z)dxdydz =\iiint\Omega F(r,\rho,\varphi)r^2sin\varphi d\varphi d\theta dr$
$\theta$摆在前,$\varphi$摆中间,r 摆最后面
其中,$F(r,\theta,\varphi) = f(rsin\varphi cos\theta,rsin\varphi sin\theta,rcos\varphi)$
适用范围
- 积分域表面用球面坐标表示时方程简单
- 被积函数用球面坐标表示时变量相互分离
三重积分对称性的重要结论
1) 若积分区域 $\Omega$ 关于xOy 坐标面对称,且 $f(x,y,z)$ 是关于z的奇函数,则 $\iiint_\Omega f(x,y,z) dv = 0$
2) 若积分区域 $\Omega$ 关于xOy 坐标面对称,且 $f(x,y,z)$ 是关于z的偶函数,则 $\iiint\Omega f(x,y,z) dv = 2\iiint\Omega f(x,y,z) dv $
仿照上述结论,不难得出积分区域关于另外两个坐标面对称,以及被积函数关于另外两个变量的奇偶性的相关结论。
重积分应用
- 能运用重积分解决的实际问题的特点
- 所求量分布在有界闭区域上的整体量
- 对区域具有可加性
- 能用重积分解决问题的方法
- 用微元分析法建立积分式
- 解题要点
- 画出积分域
- 选择坐标系
- 确定积分序
- 定出积分限
- 计算要简便
立体体积
曲顶柱体
曲顶柱体的顶为连续曲面 $z = f(x,y),(x,y)\in D$
其体积为 $V = \iint_Df(x,y)dxdy$
占有空间有界域$\Omega$的立体的体积为
$V = \iiint_\Omega dxdydz$
曲面面积

所以曲面面积公式
$A = \iint{D{xy}} \sqrt{1+f_x^2(x,y)+f_y^2(x,y)}d\sigma $
当光滑曲面的方程为$z = f(x,y)$ $(x,y) \in D_{xy} $
$A = \iint{D{xy}} \sqrt{1+(\frac{\delta z}{\delta x})^2+(\frac{\delta z}{\delta y})^2}dxdy$
光滑曲面的方程为 $y = f(z,x)$ $(z,x) \in D_{zx} $
$A = \iint{D{zx}} \sqrt{1+(\frac{\delta y}{\delta z})^2+(\frac{\delta y}{\delta x})^2}dzdx$
光滑曲面的方程为 $x = f(z,y)$ $(z,y) \in D_{zy} $
$A = \iint{D{zy}} \sqrt{1+(\frac{\delta x}{\delta z})^2+(\frac{\delta x}{\delta y})^2}dzdy$
当光滑曲面方程为隐式 $F(x,y,z)=0,F_z \neq 0 $
$\frac{\delta z}{\delta x}=-\frac{Fx}{F_z},\frac{\delta z}{\delta y}=-\frac{F_y}{F_z},(x,y)\in D{xy}$
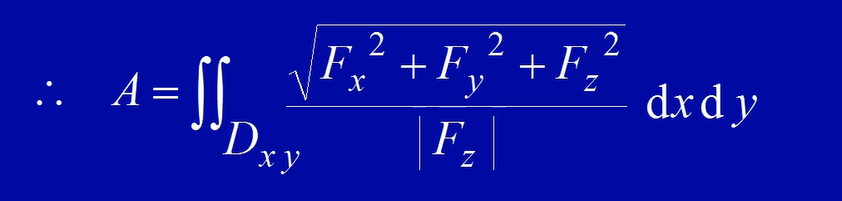
物体的质心


当所求对象是三维立体时
密度为$\rho(x,y,z)$时
令每个个小区域的最大直径$\lambda \rightarrow 0$
一般不会让我们全部求。先考虑从对称性出发,把能变成0的都变成0
$ \overline{x} = \frac{\iiint\Omega x\rho(x,y,z)dxdydz}{\iiint\Omega \rho(x,y,z)dxdydz}$
$ \overline{y} = \frac{\iiint\Omega y\rho(x,y,z)dxdydz}{\iiint\Omega \rho(x,y,z)dxdydz}$
$ \overline{z} = \frac{\iiint\Omega z\rho(x,y,z)dxdydz}{\iiint\Omega \rho(x,y,z)dxdydz}$
形心坐标:
当 $\rho = 常数$
$ \overline{x} = \frac{\iiint\Omega x dxdydz}{\iiint\Omega dxdydz}$
$ \overline{y} = \frac{\iiint\Omega y dxdydz}{\iiint\Omega dxdydz}$
$ \overline{z} = \frac{\iiint\Omega z dxdydz}{\iiint\Omega dxdydz}$
$ V = \iiint_\Omega dxdydz$
当物体时平面薄片时
密度为$\mu(x,y)$时
$ \overline{x} = \frac{\iint_D x\mu(x,y)dxdy }{\iint_D\mu(x,y)dxdy }=\frac{M_y}{M}$
$ \overline{y} = \frac{\iint_D x\mu(x,y)dxdy }{\iint_D\mu(x,y)dxdy }=\frac{M_x}{M}$
$M_x和M_y$分别时对x轴和对y轴的静矩
形心坐标 当 $\mu=常数$时
$ \overline{x} = \frac{\iint_D x dxdy }{\iint_D dxdy } $
$ \overline{y} = \frac{\iint_D x dxdy }{\iint_D dxdy } $
A = ${\iint_D dxdy }$ A是D的面积
我们要先求出A或者V ,再分别求出 $\iint_D xdxdy,\iint_D ydxdy$
物体的转动惯量

当对象是三维立体时
密度为$\rho(x,y,z)$时
因此物体对z轴的转动惯量:
$Iz = \iiint\Omega(x^2+y^2)\rho(x,y,z)dxdydz$
因此物体对x轴的转动惯量:
$Ix = \iiint\Omega(z^2+y^2)\rho(x,y,z)dxdydz$
因此物体对y轴的转动惯量:
$Iy = \iiint\Omega(x^2+z^2)\rho(x,y,z)dxdydz$
因此物体原点的转动惯量:
$IO = \iiint\Omega(x^2+z^2+z^2)\rho(x,y,z)dxdydz$
如果对象是平面薄片时
密度为$\mu(x,y)$时
物体对x轴的转动惯量:
$I_x = \iint_Dy^2\rho(x,y)dxdy$
物体对y轴的转动惯量
$I_y = \iint_Dx^2\rho(x,y)dxdy$
物体原点的转动惯量
$I_y = \iint_D(x^2+y^2)\rho(x,y)dxdy$
物体的引力

因此立体对象的引力分量
密度为$\rho(x,y,z)$
$Fx = G\iiint\Omega \frac{\rho(x,y,z)(x-x_0)}{r^3}dv$
$Fy = G\iiint\Omega \frac{\rho(x,y,z)(y-y_0)}{r^3}dv$
$Fz = G\iiint\Omega \frac{\rho(x,y,z)(z-z_0)}{r^3}dv$
求平面薄片D 的引力分量
密度为$\mu(x,y)$
$F_x = G\iint_D\frac{\mu(x,y)(x-x_0)}{r^3}d\sigma$
$F_y = G\iint_D\frac{\mu(x,y)(y-y_0)}{r^3}d\sigma$
$F_z = G\iint_D \frac{\mu(x,y)(z-z_0)}{r^3}d\sigma$ 假设薄片在xOy平面上
其中G是引力常数,r 是点与点之间的距离