高等数学多元微积分总结

Posted on
Words count in article: 4k | Reading time ≈ 16

高等数学多元微分总结

二元函数的极限

我们还是要去寻找无穷小代换。这里列出一二

$e^{xy}-1 \sim xy((x,y)\rightarrow(0,0))$

$tan xy\sim xy((x,y)\rightarrow(0,0))$

$1-cos(x) \sim \frac{1}{2}x^2$

$sin(xy)\sim xy$

全微分

全微分：$dz = \frac{\partial z}{\partial z}dx+\frac{\partial z}{\partial y}dy$

全增量： $\Delta z = f(x+Δx,y+Δy)−f(x,y)$

（偏）导数，连续函数，全微分之间的关系

示例

证明

函数的连续证明：
  1. $f(x)$在$x_0$处有定义​
  2. 极限$\lim\limits_{x\rightarrow x_0}f(x)$存在
  3. $\lim\limits_{x\rightarrow x_0}f(x)=f(x_0)$

三个条件都满足的时候，说明函数连续

偏导数连续是什么意思？

先用定义求出该点的偏导数值c,再用求导公式求出不在该点时的偏导数$fx(x,y)$,最后求$f_x(x,y)$当(x,y)趋于$(x_0,y_0)$点时的极限,如果$\lim\limits{x,y\rightarrow x_0,y_0}(x,y)=c$,即偏导数连续,否则不连续.

(偏)导数存在的证明

初等函数都是可导的，导数在$x_0$处的定义如下

$f^{‘}(x0)=\frac{\lim\limits{Δx→0}f(x_0+Δx)−f(x_0)}{Δx}$

那么以此类推，偏导数的定义就可以给出了

  • 在$(x_0,y_0)$这个点的偏导数定义

    $fx(x_0,y_0)=\frac{\lim\limits{Δx→0}f(x_0+Δx,y_0)−f(x_0,y_0)}{Δx}$

如果上面的式子存在，那么说明关于x的偏导数存在。否则就不存在

偏导数存在并不能证明函数可微分，和函数可导一样

函数可微的判断

$ρ=\sqrt{Δx^2+Δy^2}$

判断 $Δz−AΔx−BΔy=o(ρ)$

即$\lim\limits_{Δx→0,Δy→0}\frac{f(x+Δx,y+Δy)−f(x,y)−\frac{∂z}{∂x}Δx−\frac{∂z}{∂y}Δy}ρ=0$

  • 当函数可微，全微分自然存在

$dz=AΔx+BΔy+o(ρ)$

如果可微，则$A=\frac{∂z}{∂x}$,$B=\frac{∂z}{∂y}$

多元复合函数求导的注意点

  • 当出现二阶甚至高阶偏导数的时候，我们会感到异常头疼 ，时常漏乘或者漏考虑一些状况，对此我有两点要说
  • 一：在求二阶偏导数时，先求一次导数项，再求二次导数项
  • 二: 再求二阶偏导数的时候，原来的系数放左边，导数符号放中间，新导出的系数放右边

求偏导结束的时候，我们还可以自己做一遍检查，主要检查有没有一次导函数，两次导函数($f{11},f{22},f{12}$)等等，$f{12}$前后保持一致，所以是双倍。

  • 多元复合函数常常会考一些证明题
  • 示例
  • 证明题不难，只要把能化开的全部展开，再合并同类项就行，但是要细，要慢

隐函数求导

当目标函数为F(x,y,z)=0时

方法一

$\frac{∂y}{∂x}=−\frac{F_x}{F_y}$

以此类推

在做题的时候不要囫囵吞枣，要细嚼慢咽

  • 先求出Fx,Fy
  • 再写上当Fy 不为0 的时候，成立，这样更严谨
  • 最后根据公式计算
方法二

对两边求全微分,对dz,dx,dy全部求偏导

获得 $Adz=Bdx+Cdy$

那么 $\frac{dz}{dx} = \frac{B}{A},\frac{dz}{dy} = \frac{C}{A}$

  • 注意，在求隐函数二阶偏导的时候，比较复杂。下面是一个例子

示例

我们看到在虽然表面上没有x，但是z包含了x，所以对z求导以后还要乘上偏导$\frac{dz}{dx}$并展开

方法三

方程两边同时对某个量求偏导数。比如对于 $\frac{\partial z}{\partial x}$ 那就等式两边同时对x求偏导数。对$\frac{\partial z}{\partial y}$ 则同时对y求偏导数。然后合并同类项。把$\frac{\partial z}{\partial x}$ 放在一起，即可获得答案。

例题：

$x+2y+z-2\sqrt{xyz}$ 求 $\frac{\partial z}{\partial x}$

在所给方程两端对x求偏导数，并注意 $z = z(x,y)$ 得到 $1+\frac{\partial z}{\partial x}-\frac{1}{\sqrt{xyz}}(yz+xy\frac{\partial z}{\partial x}) = 0$

当 $1-\frac{xy}{\sqrt{xyz}}\neq 0$ 时，解得 $\frac{\partial z}{\partial x} = \frac{yz-\sqrt{xyz}}{\sqrt{xyz}-xy }$

当目标函数为方程组，但不是隐函数时

  • 利用线性代数中的克莱默法则求解
  • 克莱默法则，就是把x1，x2….放在左边，常数项放到右边
  • 先求出D，D就是左边未知数的系数组成的行列式。当D=0的时候，只有唯一解，D不等于0的时候，有多解
  • 一次求出D1，D2…D1行列式就是x1的系数替换成右边的常数，以此类推
  • 最后 $x_1=\frac{D1}{D},x_2=\frac{D2}{D}…..$

示例

我们可以拿第一个方程组为例

  1. 因为要求$\frac{dy}{dx},\frac{dz}{dx}$所以我们知道要两边关于x求导才能出这两个未知数
  2. 然后整理过后得到了示例
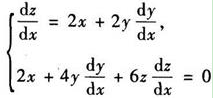
  3. 求出它的系数行列式，也就是
  4. 依次求出D1,D2，对应$\frac{dy}{dx},\frac{dz}{dx}$
  5. D1= D2 =
  6. 相除即得我们要的结果
  • 请读者自证第二小题

当目标函数为 时

  • 利用两边对x求导，像上面那种方法做

  • 利用雅可比行列式，本质上还是克莱默行列式的变形

    • 首先求出行列式 J 示例
    • 其次开始替换，要求$\frac{du}{dx}$ 那么把u的位置替换成x求行列式的值，要求$\frac{du}{dy}$ 那么就把u的位置换成y，然后乘以 -1 / J
    • 如图 示例
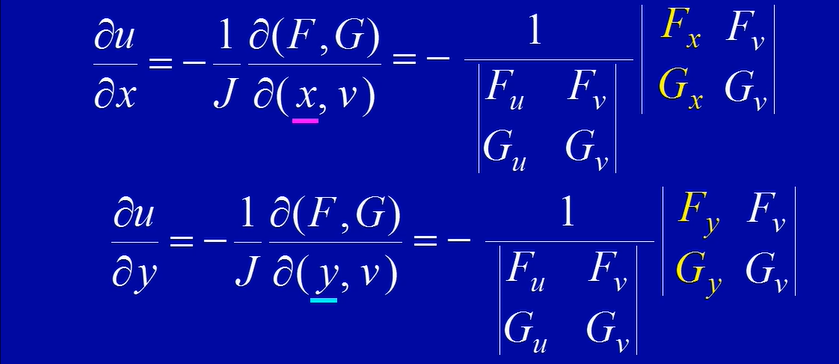
    • 此外，对于$\frac{dv}{dx},\frac{dv}{dy}$也是一样的道理
    • 所以为了方便起见，我们需要先对方程组 做一个拆分，分别求出$F_x,F_y,F_u,F_v,G_x,G_y,G_u,G_v$排列整齐就可以一目了然

示例

拿第一个方程组举例

  1. 此方程组可以确定两个二元隐函数 u= u( x , y );v=v( x , y )
  2. 要求$\frac{du}{dx},\frac{dv}{dx}$ 所以我们先要对两端关于x求偏导数
  3. 整理得到示例
  4. 解出D,D1,D2 那么就解出了最后的答案

拿第二个方程组举例

  1. 当然，这一题也可以向上面那样，两边先对x求导，根据D，D1，D2求解，但是比较繁琐。所以这里用雅可比行列式
  2. 首先把它们列成的形式示例
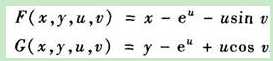
  3. 然后，我们要求出示例
  4. 最后根据题目需求，求出J和一堆行列式示例

多元函数的几何应用

一元向量值函数及其导数

示例

示例

空间间曲线的切线与法平面

当曲线为向量形式$\Gamma: x = \varphi(t) ,y = \psi(t),z=\omega(t),t\in [a,b]$的时候

根据一元向量值函数的结论，我们知道切向量就是在该点的导数

$\vec{f^{‘}(t)} = (\varphi^{‘}(t),\psi^{‘}(t),\omega^{‘}(t))$

又因为法平面的法向量和该点的切向量平行，那么我们就知道了两者形态是一样的

利用点向量式建立切线方程，利用点法式建立曲线的法平面方程如下

示例

那么如果是光滑曲线 $\Gamma: y = \psi(x),z=\omega(x)$呢？

我们把曲线看成 $\Gamma:x=x,y = \psi(x),z=\omega(x)$

然后按照上面的方法可得

$\vec{f^{‘}(t)} = (1,\psi^{‘}(x),\omega^{‘}(x))$

那么出现$y^2 = 2mx,z^2 = m-x $在点$(x_0,y_0,z_0)$处的切线及法平面方程这种题目怎么解决呢？用全微分的方法来做。

$\vec{T} = (1,\frac{dy}{dx}|_M,\frac{dz}{dx}|_M)$

当曲线为一般形式的时候的时候

在点$M(x_0,y_0,z_0)$处的切向量为，记住后面那个

$\vec T= J(1,\frac{1}{J}\frac{∂(F,G)}{∂(z,x)}∣_M,\frac{1}{J}\frac{∂(F,G)}{∂(x,y)}∣_M)=(\frac{∂(F,G)}{∂(y,z)}|_M,\frac{∂(F,G)}{∂(z,x)}∣_M,\frac{∂(F,G)}{∂(x,y)}|_M)$

这是记忆方法，如果求x处的坐标，那么就转两位 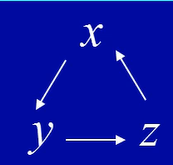示例

所以根据切向量，可以得到斜线方程和法平面方程

示例

两者可以用全微分的方法来做，也可以得到切向量

具体的做法，和隐函数求导一样，两边对x求导，然后根据D，D1，D2解出$\frac{dy}{dx},\frac{dz}{dx}$ 切向量$\vec{T} = (1,\frac{dy}{dx}|_M,\frac{dz}{dx}|_M)$

曲面的切平面与法线

曲面$\Sigma$在点M在的法向量，就是法线的线向量和切平面的法向量

求x处法向量，就是曲面$\Sigma$对x的偏导，以此类推

$\vec n = (F_x(x_0,y_0,z_0),F_y(x_0,y_0,z_0),F_z(x_0,y_0,z_0))$

于是可以求出法线方程和切平面方程

示例

几何问题中的几类题

  • 归根到底就是1.找出法向量 2.找向量之间的关系
  1. 告诉你曲线方程，让你求某点的切线和法平面
    1. $\vec{f^{‘}(t)} = (\varphi^{‘}(t),\psi^{‘}(t),\omega^{‘}(t))$或者$\vec{T} = (1,\frac{dy}{dx}|_M,\frac{dz}{dx}|_M)$
  2. 告诉你曲面方程，让你求某点的切平面和法线
    1. $\vec n = (F_x(x_0,y_0,z_0),F_y(x_0,y_0,z_0),F_z(x_0,y_0,z_0))$
  3. 告诉你曲面方程，让你求某点的切平面与某个面的夹角的余弦值
    1. 找到曲面在该点的法向量
    2. 找到某个面的法向量
    3. 求这两个法向量的余弦值，就是我们所要的余弦值
  4. 让你求一条曲线上平行于某平面的切线，求出该点和该线
    1. 找到曲线一般的切向量
    2. 通过该向量*某平面的法向量 = 0 构造方程
    3. 解出该方程或者拿到变量之间的关系，回代曲线方程求解
  5. 让你求一条曲线上平行于某平面的法平面，求出该点和该面
    1. 找到曲线的一般切向量，也就是该点出法平面的法向量
    2. 该切向量和目标平面的法向量平行，得到一个方程
    3. 解方程或者回代
  6. 让你求一个曲面上平行于某平面的切平面，求出该点和该面
    1. 找到曲面的一般法向量，那么这个就是切平面的法向量
    2. 该法向量与目标平面的法向量平行，得到方程
    3. 解方程或者回代
  7. 让你求一个曲面上平行于某平面的法线，求出该点和该面
    1. 找到曲面的一般法向量，那么这个就是切线的向量
    2. 该向量与目标平面的法向量垂直，得到方程
    3. 解方程或者回代
  8. 或者和某直线平行或者垂直，归根到底就是找向量之间的关系

方向导数与梯度

方向导数

  • 对于三元函数，如果在点P(x,y,z)处可微，则函数在该店沿任意方向l的方向导数都存在
  • $\frac{∂f}{∂l}=\frac{∂f}{∂x}\cos\alpha+\frac{∂f}{∂y}\cos\beta+\frac{∂f}{∂z}\cos\gamma$
  • 对于二元函数，在点P(x,y)处沿方向l 的方向导数是
  • $\frac{∂f}{∂l}=\frac{∂f}{∂x}\cos\alpha+\frac{∂f}{∂y}\cos\beta$
  • 特别的：当l与x轴同向有 $\frac{∂f}{∂l}=\frac{∂f}{∂x}$
  • 当l与x轴反向向有 $\frac{∂f}{∂l}=-\frac{∂f}{∂x}$
  • 外法线是正的，内法线为负
题形

  • 给你一个函数，让你求在某点沿着一个向量的方向导数

    • 先计算 向量的方向余弦
    • 把方向余弦分别乘以函数对x,y,z的偏导数
    • 把P点带入后相加

  • 给你一个函数，让你求在某点沿着某一条曲线朝着某个方向增大的方向导数

    • 先计算某条曲线在该点处的方向向量
    • 计算该方向向量的方向余弦
    • 方向余弦与偏导对应相乘
    • 把P点带入后相加

  • 总之，计算方向导数的题目，我们要找到三个信息

      1. 就是方向向量，依次求出方向余弦
      2. 找到目标函数，对变量求偏导
      3. 找到该点，带入

  • 计算时要规范，否则容易代入时出错：

    • $\frac{\partial u}{\partial x}= \cdots ,\frac{\partial u}{\partial y} = \cdots,\frac{\partial u}{\partial z}=\cdots$
    • $\dfrac{\partial u}{\partial x}|{( x_0,y_0,z_0)}=\cdots , \dfrac{\partial u}{\partial y}|{( x0,y_0,z_0)}=\cdots , \dfrac{\partial u}{\partial z}|{( x_0,y_0,z_0)}=\cdots$
    • $e_1$代表方向向量，$|e_1| = 1，\Rightarrow e_1 =(cos\alpha,cos\beta,cos\gamma)$
    • 所以:$\frac{\partial u}{\partial l}|_{(x_0,y_0,z_0)} = \frac{∂f}{∂x}\cos\alpha+\frac{∂f}{∂y}\cos\beta+\frac{∂f}{∂z}\cos\gamma = \cdots$

梯度

示例

那么，向量$\vec G$被称为函数 f(P)在P处的梯度，记作grad f(P)

$gradf(P) = \nabla f(P) = (f_x(P),f_y(P),f_z(P))$

当函数为二元函数f(x,y)在 P（x,y) 处的梯度

$grad f(P) = \nabla f(P) = (f_x(P),f_y(P))$

几何意义

函数在同一点的梯度垂直于该点的等值线，指向函数增大的方向

特点
  1. 方向： f变化率最快的方向
  2. 模： f的最大变化率的值
关系

所以，函数的方向导数为梯度在该方向上的投影：

$\frac{∂f}{∂l} = grad f\cdot\vec {e_l}$

示例

运算

示例

题形
  • 给你一个函数，要你求出在某点沿增加最快方向的方向导数
    • 最快方向就是该点的梯度向量
    • 此时方向导数就是该向量的模
    • 特别要注意的是，要你求梯度，求的是一个向量而不是一个模
  • 值得注意的是，变化最快包含了增加最快和减少最快，但是我们常常忽略负的那个在答题的时候一定要全写

物理意义

多元函数的极值

多元函数的极值

  • 必要条件： 函数 z = f(x,y) 在点$(x_0,y_0)$存在偏导数，且在该点取极值那么我们一定可以得到 $f^{‘}_x(x_0,y_0)= 0,f^{‘}_y(x_0,y_0)= 0$
    • 需要注意的是， 让偏导数都为0的点被称为驻点，但是驻点不一定是极值点
    • 如 z = xy 有驻点（0，0）但是（0，0) 不是一个极值点
  • 充分条件: 如果函数z =f(x,y)在点$(x0,y_0)$的某个邻域内具有一阶和二阶连续偏导数，且$f^{‘}_x(x_0,y_0)= 0,f^{‘}_y(x_0,y_0)= 0$ 那么，我们再进一步令$A = f{xx}(x0,y_0),B = f{xy}(x0,y_0),C = f{yy}(x_0,y_0)$
    • 当 $AC-B^2>0$时，具有极值
    • 当$AC-B^2<0$时，没有极值
    • 当$AC-B^2=0$时，不能确定，需要另行讨论
题型
  • 这类考察基本概念和定义

示例

  • 求函数 f(x,y)的极值
    • 先求出驻点
    • 求出二阶偏导数
    • 判断驻点是否符合极值点条件

最值应用问题

条件极值

  • 对自变量除了定义域的限制之外，还有其它条件的限制
方法1：代入法

在条件$\varphi(x,y) = 0$下，求出z = f(x,y)的极值

  • 先从条件$\varphi(x,y) = 0$中解处 $y = \psi(x)$
  • 带入函数z = f(x,y)当中
  • 解决一元函数 $z = f(x,\psi(x))$的无条件极值问题
方法2 : 拉格朗日乘数法

在条件$\varphi(x,y) = 0$下，求出z = f(x,y)的极值

示例

所以极值点必然满足

引入辅助函数 $F = f(x,y)+\lambda\varphi(x,y)$

那么极值点满足

可以看见下面的关系式就是上面的关系式，于是，辅助函数F的极值点就是 z = f(x,y)的极值点，辅助函数被称为拉格朗日函数。

然后。根据这几个方程找出可疑的极值点，再加以验证

  • 推广：示例
-------------本文结束，感谢您的阅读-------------