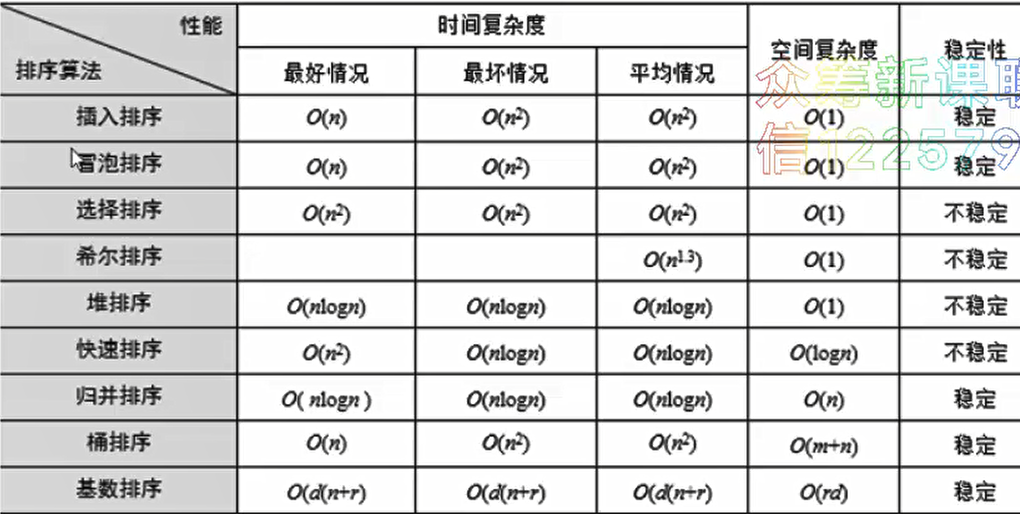
分配排序

Posted on | In
Words count in article: 2.5k | Reading time ≈ 10

分配排序

桶排序

  • 分配排序不需要比较关键词的大小，根据关键词各位上的值，进行若干次分配和收集实现排序
  • 桶排序将待排序序列划分成若干区间。每个区间形象的看作一个桶，如果桶中的记录多以一个则使用较快的排序方法进行排序，把每个桶中的记录收集起来，最终得到有序序列

示例

注意的问题

  • 桶排序的数据最好是均匀分布的，如果都在90分以上，那么都在一个桶内，那么就退化成了一般的排序。在理想的情况下，当数据均匀分布，桶的数量m足够大的时候，那么每一个桶内最多只有一个记录，不需要再进行排序，只需要O（N）的时间将所有的记录分配到桶中，再用O（N）的时间收集起来。但这样空间复杂度会很大
  • 桶排序支队不同的数据选择的划分方法是不同的，例如序列（2，46，1278，89323，211，22，43，1）可以按照位数划分桶，1位数，2位数，3位数…
  • 桶内排序的时候使用的比较排序算法也有可能不同，可以用插入排序，也可以用快速排序

基数排序

  • 基数排序可以看作桶排序的一种扩展，是一种多关键词排序算法，如果记录按照多个关键词排序，则依次按照这些关键词进行排序。如果记录按照一个数值型的关键词排序，可以把该关键词看作是d位组成的多关键词排序，每一位的取值范围是[0,r)，其中r被称为基数。例如十进制数268由3位数组成，每一位取值都在[0,10)，十进制数的r为10，二进制为2，英文字母的基数为26.

算法步骤

  1. 求出待排序序列中最大关键词的位数d，然后从低位到高位进行基数排序
  2. 按个位将关键词依次分配到桶中，然后把每个桶中的数据依次收集起来
  3. 将十位关键词依次分配到桶中，然后把每个桶中的数据依次收集起来
  4. 依次下去，直到d位处理完毕，得到一个有序的序列
  5. 拿68，75，54，70，83，48，80，12，92为例子
  • 先按个位排序
0 1 2 3 4 5 6 7 8 9
70 12 83 54 75 68
80 92 48
  • 按找桶的顺序收集，波浪化收集得到 70，80，12，92，83，54，75，68，48
  • 再按照第一趟的排序结果十位排序
0 1 2 3 4 5 6 7 8 9
12 48 54 68 70 80 92
75 83
  • 再按照桶的顺序收集，得到12，48，54，68，70，75，80，83，92

讨论

  • 为啥一定要依次收集？如果不依次会怎么样
  • 示例
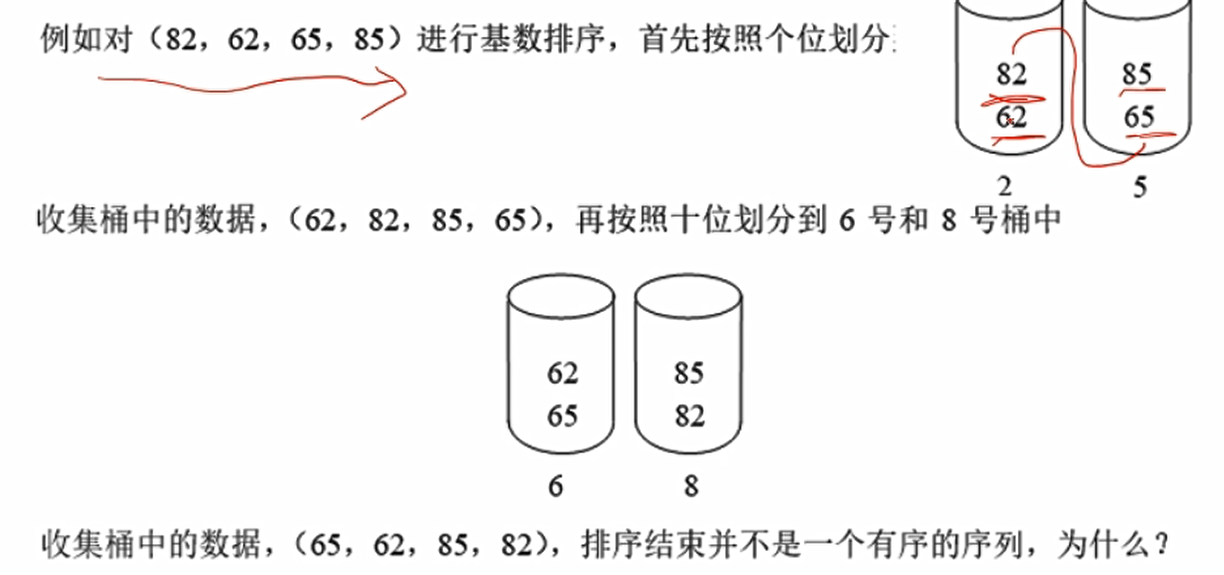
  • 因为在十位相同的数字，在它们个位排序的时候，桶标号较小的肯定要比桶标号大的要小，所以在收集生成序列的时候也要先于大的，这样在按照十位排序的时候小的先于大的入桶，达到排序目的
  • 所以要用一个队列，先进先出，依次进行。可以采用队列保持桶中数据的进出顺序，从而保证排序结果的正确性。也就是说每一个桶内使用一个队列存储数据，可以使用顺序队列或者链式队列

算法复杂度分析

  • 基数排序需要进行d次排序，每一次排序包含分配和收集两个操作，分配需要O(n)的时间，收集操作如果使用顺序队列也要O(n)的时间，如果使用链式队列则只需要将r个链队首尾相连即可，需要O(r)的时间，总的时间复杂度为O(d(n+r))
  • 如果使用顺序队列，需要r个大小为n的队列，空间复杂度为O(rn)。如果使用链式队列，则需要额外的指针域，那么空间复杂度O(n+r)，比顺序队列的空间要少得多
  • 基数排序时按关键字出现的顺序依次进行的，是稳定的排序方法
  • 桶中的多个数据元素可以采用二维数组，链式存储，也可以采用一维辅助数组进行处理。

代码

二维数组代码的实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include<bits/stdc++.h>
using namespace std;
# define Maxsize 10000
int A[Maxsize];
//求出待排序序列中最大的元素位数
int Maxbit(int A[],int n){
    int maxvalue = A[0],digits = 0;
    for(int i = 1;i<n;i++)
    {
        if(A[i]>maxvalue)
            maxvalue = A[i];
    }
    while(maxvalue!= 0)
    {
        digits++;
        maxvalue/=10;
    }
    return digits;
}
// 求xbit位上的数字，如238上的第2位上的数字是3
// bit = 1的时候，那么就是8
int Bitnumber(int x,int bit)
{
    int temp = 1;
    for(int i = 1;i<bit;i++)
    {
        temp*=10;
    }
    return (x/temp)%10;
}
// 算法函数
void RadixSort(int A[],int n)
{
    int i ,j,k,bit,maxbit;
    maxbit = Maxbit(A,n);
    //构造一个动态二位数组
    int **B= new int *[10];
    for(i = 0;i<10;i++)
        B[i] = new int[n+1];//第0位存储元素个数
    for(i = 0;i<10;i++)
    {
        B[i][0] = 0;//先把元素个数默认为0
    }
    //这里开始进行分配收集操作，一共进行maxbit次
    for(bit = 1;bit<=maxbit;bit++)
    {
        //分配操作
        for(j = 0;j<n;j++)
        {
            //取出位数
            int num = Bitnumber(A[j],bit);
            //然后给A[j]分配桶内位置
            int index = ++B[num][0];
            //存储
            B[num][index] = A[j];
        }
        //收集操作，一共有10个桶，那么一一串连
        for(i = 0,j = 0;i<10;i++)
        {
            for(k=1;k<=B[i][0];k++)
                A[j++] = B[i][k];
            //更新原来序列，因为j一直在加，最后会把原来的序列全更新一遍
            B[i][0]=0;//收集完这个桶后元素置0
        }
    }
    //销毁数组
    for(i = 0;i<10;i++)
    {
        delete []B[i];
    }
    delete B;
}

int main()
{
    int n ;
    cout<<"请输入数列中的元素个数"<<endl;
    cin>>n;
    cout<<"请依次输入数列中的元素"<<endl;
    for(int i = 0;i<n;i++)
    {
        cin>>A[i];
    }
    RadixSort(A,n);
    cout<<"基数排序的结果:"<<endl;
    for(int i = 0;i<n;i++)
    {
        cout<<A[i]<<" ";
    }
    cout<<endl;

   return 0;
}
一维数组实现
  • 利用计数器数组计数
  • 计数器累加
  • 把数据反向遍历存储到临时数组中，这里如果用正向遍历，就不能正确输入数据了，在每次输入的时候，计数器相应元素-1，这样能实现巧妙地映射。最后会变成上一格的计数器的数字
  • 示例
  • 临时数组对原数组实现覆盖

拿68，75，54，70，83，48，80，12，75*，92举例

第一次循环

  • 先计数
  • 示例
0 1 2 3 4 5 6 7 8 9
2 0 2 1 1 2 0 0 2 0
  • count数组累加
    | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
    | —— | —— | —— | —— | —— | —— | —— | —— | —— | —— |
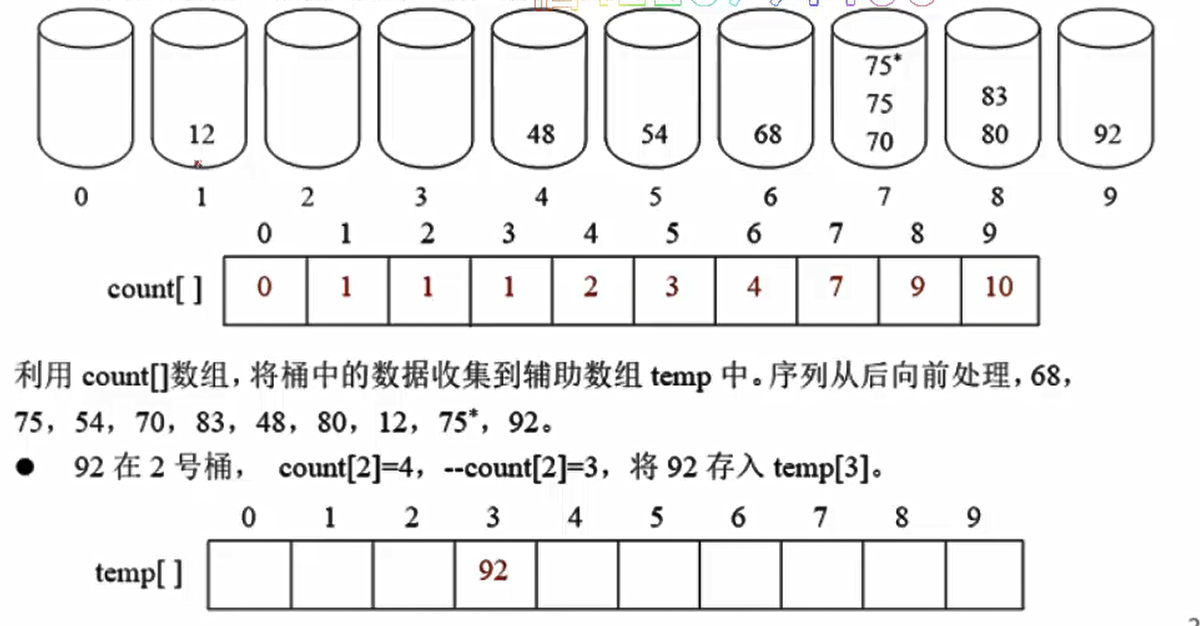
    | 2 | 2 | 3 | 5 | 6 | 8 | 8 | 8 | 10 | 10 |
  • 68，75，54，70，83，48，80，12，75*，92 反向遍历，放入temp数组
  • 拿到92，个位数是2，那么看到2的count数组对应4，因为我们是从0开始计数的，所以92放到temp[3]中，同时count[2]—

count

0 1 2 3 4 5 6 7 8 9
2 2 3 5 6 8 8 8 10 10

temp

0 1 2 3 4 5 6 7 8 9
92
  • 以此类推，那么最后的结果就是这样

count

0 1 2 3 4 5 6 7 8 9
0 2 2 4 5 6 8 8 8 10

temp

0 1 2 3 4 5 6 7 8 9
70 80 12 92 83 54 75 75* 68 48

第二次循环
70 ， 80 ， 12 ， 92 ， 83 ， 54 ， 75 ， 75* ， 68 ， 48

  • 先计数
  • 示例
0 1 2 3 4 5 6 7 8 9
0 1 0 0 1 1 1 3 2 1
  • count累加
    | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
    | —— | —— | —— | —— | —— | —— | —— | —— | —— | —— |
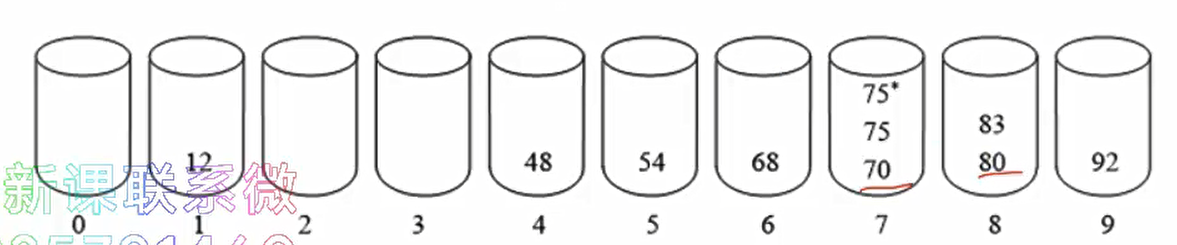
    | 0 | 1 | 1 | 1 | 2 | 3 | 4 | 7 | 9 | 10 |
  • 以此类推，那么最后的结果就是这样

count

0 1 2 3 4 5 6 7 8 9
0 0 1 1 1 2 3 4 7 9

temp

0 1 2 3 4 5 6 7 8 9
12 48 54 68 70 75 75* 80 83 92

示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include<iostream>
using namespace std;
const int maxn=1000;
int a[maxn],n;
int maxbit(int data[], int n) //辅助函数，求数据的最大位数
{
    //扫描一遍就可以了，判断是不是比10，1000大
    int d=1;//统计最大的位数
    int p=10;
    for(int i=0;i<n;++i)
    {
        while(data[i]>=p)
        {
            p*=10;
            ++d;
        }
    }
    return d;
}
void radixsort(int data[], int n) //基数排序
{
    int d=maxbit(data,n); //求最大位数
    int *tmp=new int[n]; //辅助数组
    int *count=new int[10]; //计数器
    int i,j,k;
    int radix=1;
    for(i=1;i<=d;i++) //进行d次排序
    {
        for(j=0;j<10;j++)
            count[j]=0; //每次分配前清空计数器
        for(j=0;j<n;j++)
        {
            k=(data[j]/radix)%10; //取出个位数，然后是十位数，...
            count[k]++; //统计每个桶中的记录数
        }
        for(j=1;j<10;j++)
            count[j]+=count[j-1]; //将tmp中的位置依次分配给每个桶
        for(j=n-1;j>=0;j--) //将所有桶中记录依次收集到tmp中
        {
            k=(data[j]/radix)%10;
            tmp[--count[k]]=data[j];
        }
        for(j=0;j<n;j++) //将临时数组的内容复制到data中
            data[j]=tmp[j];
        cout<<"第"<<i<<"次排序结果："<<endl;
        for(int i=0;i<n;i++)
            cout<<data[i]<<"\t";
        cout<<endl;
        radix=radix*10;
    }
    delete[]tmp;
    delete[]count;
}

int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
        cin>>a[i];
    radixsort(a,n);
    return 0;
}

加一段基数排序的gif，更容易理解

示例

视频来自可视化算法网站https://visualgo.net/zh

总结

示例

示例

-------------本文结束，感谢您的阅读-------------