归并排序

Posted on | In
Words count in article: 937 | Reading time ≈ 4

归并排序

算法设计

归并排序采用分治策略实现对n个元素进行排序算法，是分治法的一个典型应用和完美体现，它是一种平衡，简单的二分分治策略，过程大致分为：

  1. 分解——将待排序的元素分成大小大致相同的两个子序列
  2. 治理——对两个子序列进行合并排序
  3. 合并——将排好序的有序子序列进行合并，得到最终的有序列。

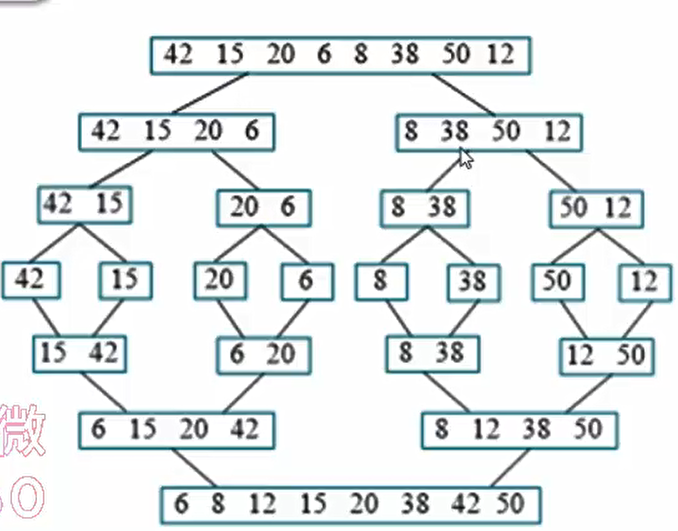示例递归树高nlogn

合并操作

  • 新开辟一段数组，数组长为 $high- low +1$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
void merge(int arr[],int low,int mid,int high)
{
    int *temp = new int [high- low +1];
    int i = low;//左序列指针
    int j = mid+1;//右序列指针
    int t = 0;//临时数组指针
    while (i<=mid && j<= high){
        if(arr[i]<=arr[j])
        { temp[t++] = arr[i++]; }
        else
        { temp[t++] = arr[j++]; }
    }
    while(i<=mid){//将左边剩余元素填充进temp中
        temp[t++] = arr[i++];
    }
    while(j<=high){//将右序列剩余元素填充进temp中
        temp[t++] = arr[j++];
    }
    t = 0;
    //将temp中的元素全部拷贝到原数组中,因为temp只是一个辅助数组
    while(low <=  high){ arr[low++] = temp[t++]; }
    delete []temp;
}

递归操作

1
2
3
4
5
6
7
8
9
10
11
12
13
void MergeSort(int A[],int low,int high)
{
    if(low<high)
    {
        int mid = (low+high)/2;
        //对A[low:mid]中的元素进行合并排序
        MergeSort(A,low,mid);
        //对A[mid+1:high]中的元素进行合并排序
        MergeSort(A,mid+1,high);
        //合并操作,两个有序序列的合并
        merge(A,low,mid,high);
    }
}

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include<bits/stdc++.h>
using namespace std;
# define Maxsize 10000
int A[Maxsize];
void Merge(int A[], int low, int mid, int high)//合并函数
{
    int *B=new int[high-low+1];//申请一个辅助数组
    int i=low, j=mid+1, k=0;
    while(i<=mid && j<=high) {//按从小到大存放到辅助数组B[]中
        if(A[i]<=A[j])
            B[k++]=A[i++];
        else
            B[k++]=A[j++];
    }
    while(i<=mid) B[k++]=A[i++];//将数组中剩下的元素放置B中
    while(j<=high) B[k++]=A[j++];
    for(i=low, k=0; i<=high; i++)
        A[i]=B[k++];
    delete []B;//释放空间
}

void MergeSort(int A[],int low,int high)
{
    if(low<high)
    {
        int mid = (low+high)/2;
        //对A[low:mid]中的元素进行合并排序
        MergeSort(A,low,mid);
        //对A[mid+1:high]中的元素进行合并排序
        MergeSort(A,mid+1,high);
        //合并操作,两个有序序列的合并
        Merge(A,low,mid,high);
    }
}
int main()
{
    int n ;
    cout<<"请输入数列中的元素个数"<<endl;
    cin>>n;
    cout<<"请依次输入数列中的元素"<<endl;
    for(int i = 0;i<n;i++)
    {
        cin>>A[i];
    }
    MergeSort(A,0,n-1);
    cout<<"快速排序的结果:"<<endl;
    for(int i = 0;i<n;i++)
    {
        cout<<A[i]<<" ";
    }
    cout<<endl;
    return 0;
}

算法分析

时间复杂度

  1. 分解： 这一步仅仅是计算出子序列的中间位置，需要常数时间O(1)
  2. 解决子问题：递归求解两个规模为n/2的子问题，所需时间为2T(n/2)
  3. 合并： Merge算法可以在O（n)的时间完成

所以运行总时间为

空间复杂度

程序中变量占用了一些辅助空间，这些辅助空间都是常数阶的，每调用一个适当大小的缓冲去，且退出时会释放。最多分配大小为n，所以空间复杂度为O(n),递归调用所使用的栈空间是O(logn) 因为递归树高logn

示例

最后贴一段gif,便于理解

示例

视频来自于可视化算法网站 https://visualgo.net/zh

-------------本文结束，感谢您的阅读-------------