快速排序
快速排序的基本思想是基于分治策略的,其算法思想如下
- 分解:先从数列中取出一个元素作为基准元素,以基准元素为标准,将问题分解为两个子序列,让小于或等于基准元素的子序列在左侧,让大于基准元素的子序列在右侧
- 治理:对两个子序列进行快速排序
- 合并:将排好序的两个子序列合并在一起(快速排序什么都不用做)
思考
如何分解是一个难题,因为如果基准元素选取不当,有可能分解成规模为0,n-1 的量的子序列,那么这样快速排序就退化为冒泡排序了。一般来说,基准元素选取有以下几种方法
取第一个元素
取最后一个元素
取中间位置的元素
取第一个,最后一个,和中间位置元素三者中的中位数
取第一个和最后一个位置之间的随机数k,(low<=k<=high)选R[k]做基准元素,可以避免每次都他妈的最坏8
1 | srand(time(0)); //选时间做种子 |
算法步骤
- 首先取数组的第一个元素作为基准元素 pivot = R[low], i = low ,j = high
- 从右向左扫描,找到小于等于pivot的数,如果找到,R[i]和R[j] 交换,i++
- 从左向右扫描,找到大于等于pivot的数,如果找到,R[i]和R[j] 交换,j —
- 重复步骤2-3,直到i和j指针重合,返回该位置mid=i 该位置的数正好是pivot元素
- 至此完成一趟排序,此时mid为界,将元数据分为两个子序列,左侧子序列元素都比pivot小,右边都比pivot大,然后再分别对这两个子序列进行快排
举例
| low,i | high,j | |||||||
|---|---|---|---|---|---|---|---|---|
| 30 | 24 | 5 | 58 | 18 | 36 | 12 | 42 | 39 |
| low | i | j | high | |||||
|---|---|---|---|---|---|---|---|---|
| 12 | 24 | 5 | 58 | 18 | 36 | 30 | 42 | 39 |
| low | i | j | high | |||||
|---|---|---|---|---|---|---|---|---|
| 12 | 24 | 5 | 30 | 18 | 36 | 58 | 42 | 39 |
| low | mid-1 | j,i,mid | mid+1 | high | ||||
|---|---|---|---|---|---|---|---|---|
| 12 | 24 | 5 | 18 | 30 | 36 | 58 | 42 | 39 |
代码实现
1 |
|
算法分析
最好情况
时间复杂度
- 分解:划分Partition需要扫描每个元素,每次扫描的元素个数不超过n,因此时间复杂度为O(n)
- 治理:在理想情况下,每次划分将问题分解为两个规模为n/2的子问题,递归求解连个规模为 n/2的自问题,所需的时间为 2T(n/2)
- 合并:因为是原地排序,合并操作不需要时间复杂度

- 最终 $T(n) = 2^xT(\frac{n}{2^x})+xO(n),x = \log n$
- 所以 代入得 $T(n) = nT(1)+\log n\times O(n)= O(n\log n)$
空间复杂度
- 程序中变量占用了一些辅助空间,这些辅助空间都是常数阶的。递归调用所使用的栈空间为递归树的深度 $\log n$ ,那么空间复杂度为$ O(\log n)$
最坏情况
时间复杂度
- 分解:划分Partition需要扫描每个元素,每次扫描的元素个数不超过n,因此时间复杂度为O(n)
- 治理:在最坏的情况下,每次划分将问题分解后,基准元素的左侧(或者右侧) 没有元素,基准元素的另一侧为1个规模为n-1的子问题。递归求解这个规模为n-1的子问题,所需的时间为T(n-1)
- 合并:因为是原地排序,合并操作不需要时间复杂度
- 相当于冒泡排序,这种情况下最坏的时间复杂度为$O(n^2)$
空间复杂度
- 程序中变量占用了一些辅助空间,这些辅助空间都是常数阶的。递归调用所使用的栈空间为递归树的深度 n ,那么空间复杂度为 O(n),因为递归调用了n次
平均情况
时间复杂度
假设我们划分后基准元素的位置在第k个
$T(n) = \frac 1{n}\sum_1^n(T(n-k)+T(n-1))+O(n)$
$= \frac1{n}(T(n-1)+T(0)+T(n-2)+T(1)+…+T(1)+T(n-2)+T(0)+T(n-1))+O(n)$
$=\frac2{n}\sum_{k=1}^{n-1}T(k)+O(n)$
用归纳法可得出,时间复杂度也为$O(n\log n)$
空间复杂度
- 程序中变量占用了一些辅助空间,这些辅助空间都是常数阶的。递归调用所使用的栈空间为递归树的深度 logn ,那么空间复杂度为 O(logn)
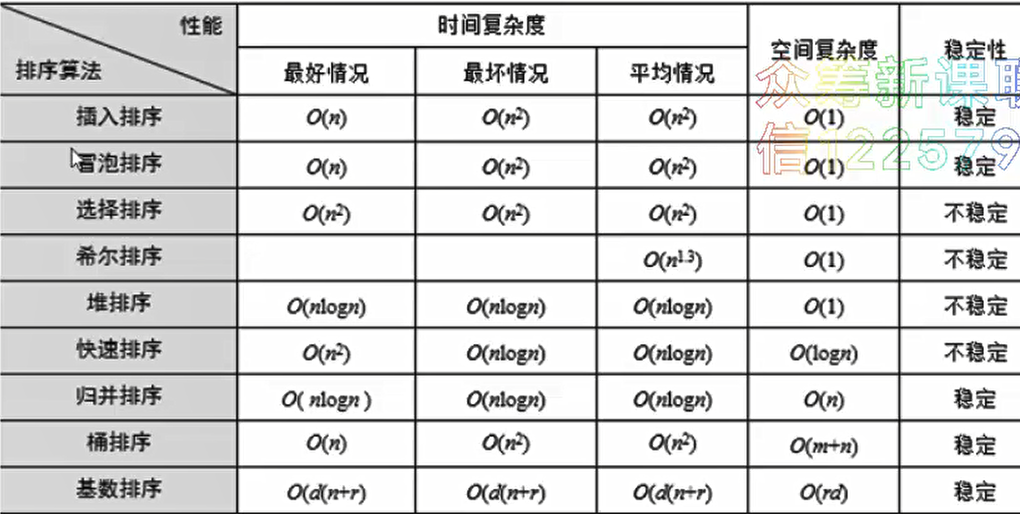
稳定性
因为前后两个方向扫描并交换,相等的两个元素有可能出现排序前后位置不一样的情况,因此快速排序是不稳定的排序方法,比如题目告诉你 70 70 排序后第一个70仍然要在第二个70之前,这时候就不能用快速排序了
算法改进
- 从上述算法可以看出,每次交换都是在和基准元素进行交换,实际上没必要这么做,我们的目的就是想把原序列分成以基准元素为界的两个子序列,左侧子序列小于等于基准元素,右侧子序列大于基准元素。
- 那么有很多方法可以实现,我们可以从右向左扫描,找到小于pivot的数R[j],让R[i]与R[j]交换,一直交替进行贸易直到i和j碰头为止,这时将基准元素与R[i]交换即可。这样完成一次划分过程交换的元素个数就少了很多
| low,i | high,j | |||||||
|---|---|---|---|---|---|---|---|---|
| 30 | 24 | 5 | 58 | 18 | 36 | 12 | 42 | 39 |
| low | i | j | high | |||||
|---|---|---|---|---|---|---|---|---|
| 30 | 24 | 5 | 12 | 18 | 36 | 58 | 42 | 39 |
| low | i,j | high,j | ||||||
|---|---|---|---|---|---|---|---|---|
| 30 | 24 | 5 | 12 | 18 | 36 | 58 | 42 | 39 |
| low | i,j | high | ||||||
|---|---|---|---|---|---|---|---|---|
| 18 | 24 | 5 | 12 | 30 | 36 | 58 | 42 | 39 |
- 优化算法降低时间空间复杂度是很难的,但是常数级的优化是容易的
1 | int Partition(int r[],int low,int high)//划分函数 |
练习题
- 设线性表中每个元素都有两个数据项$k_1$ 和 $k_2$ ,现对线性表按以下规则进行排序:先看数据项 $k_1$ , $k_1$值小的元素在前,大的再后;在k1值相同的情况下,再看k2, k2值小的在钱,大的元素在后。满足这种要求的排序方法是:
- 先按$k_1$ 进行直接插入排序,再按$k_2$ 进行简单选择排序
- 先按$k_2$ 进行直接插入排序,再按$k_1$ 进行简单选择排序
- 先按$k_1$ 进行简单选择排序,再按$k_2$ 进行直接插入排序
- 先按$k_2$ 进行简单选择排序,再按$k_1$ 进行直接插入排序
答案是D,由于整体按照k1顺序排列,所以要先排k2,再排k1,然后考虑稳定性,排完k2之后,排k1时不能打乱前后顺序,因此在k1的算法选择上一定要选稳定排序。