堆排序

Posted on | In
Words count in article: 2.9k | Reading time ≈ 11

堆排序

  • 堆排序是一种树形选择排序算法，简单选择排序算法每次选择一个关键词最小的记录需要O(n)的时间，而堆排序选择一个关键词最小的机组只需要O(logn)的时间
  • 堆可以看作一颗完全二叉树的顺序存储结构，在这颗完全二叉树中，如果每一个节点的值都大于等于左右孩子的值，称为最大堆。如果每一个节点的值都小于等于左右孩子的值，成为最小堆。左右孩子谁大谁小不要求。
  • 完全二叉树中除了最后一层，其他节点都是满的。最后一层是从左到右按照顺序出现的

完全二叉树举例

示例

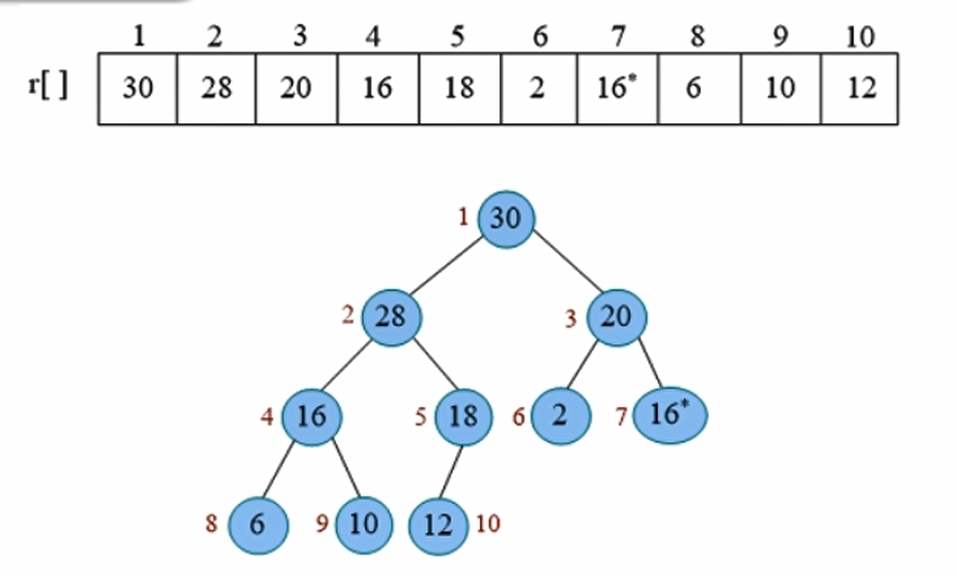
  • 完全二叉树可以顺序存储，存到一个数组当中。上面的二叉树是一个最大堆。

  • 如果这是一个完全二叉树，那么这个节点键值为i的左孩子一定是2i，右孩子一定是2i+1.他的父亲节点一定是i/2.

  • 根据完全二叉树的性值，如果一个节点的下标为i,其左孩子下标为2i,其有孩子下标为2i+1,其双亲的下标为i/2.且具有n个节点的完全二叉树的深度为$\log_2n +1$

  • 堆排序充分利用堆顶记录最大最小的性质进行排序，每次将对顶的记录交换到最后，剩余记录调整为堆即可

算法步骤

  1. 构建初始堆
  2. 堆顶和最后一个记录交换，即r[1]和r[n]交换，将r[1…n-1]重新调整为堆
  3. 堆顶和最后一个记录交换，即r[1]和r[n-1]交换，将r[1…n-2]重新调整为堆
  4. 循环n-1次，得到一个有序序列

因为构建初始堆需要反复调整为堆，所以先说明如何调整堆，然后再讲解如何构建初始堆，然后再讲解如何构建初始堆，进行堆排序

调整堆（下沉）

  • 交换后除了堆顶之外，其他节点都满足最大堆的定义，只需要将堆顶执行“下沉”操作就行了。
  • “下沉”操作：堆顶与左右孩子比较，如果比孩子大，则调整为堆；如果比孩子小，则与较大的孩子交换，交换到新的位置后，继续向下比较，从根节点一直比较到叶子
  • 排好序之后，根节点就不在堆之内了
  • 下面是一个在最大堆中提取根节点后的调整堆操作，可以清楚的观察到是如何比较完成下沉的

示例

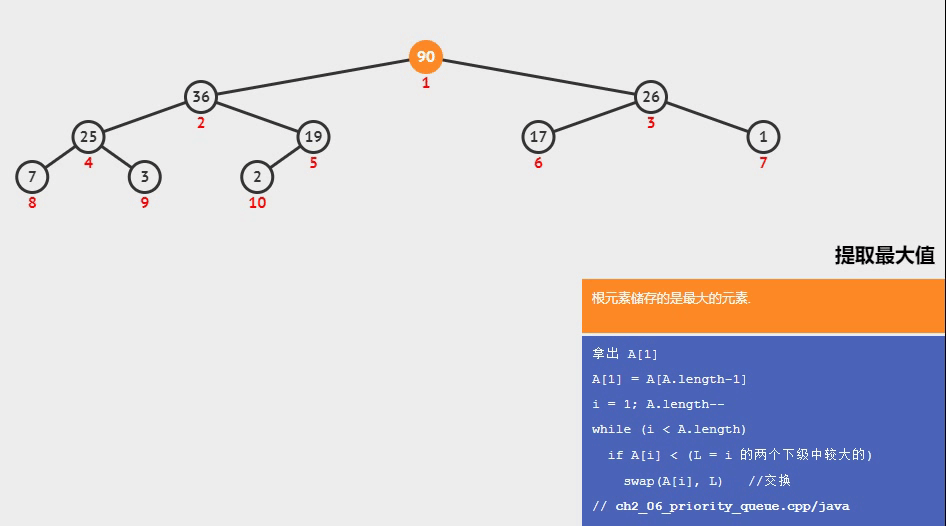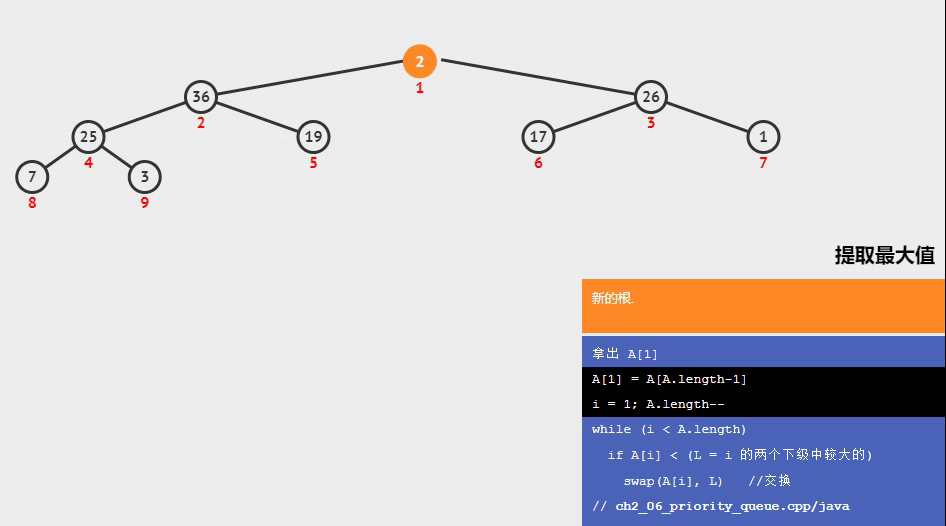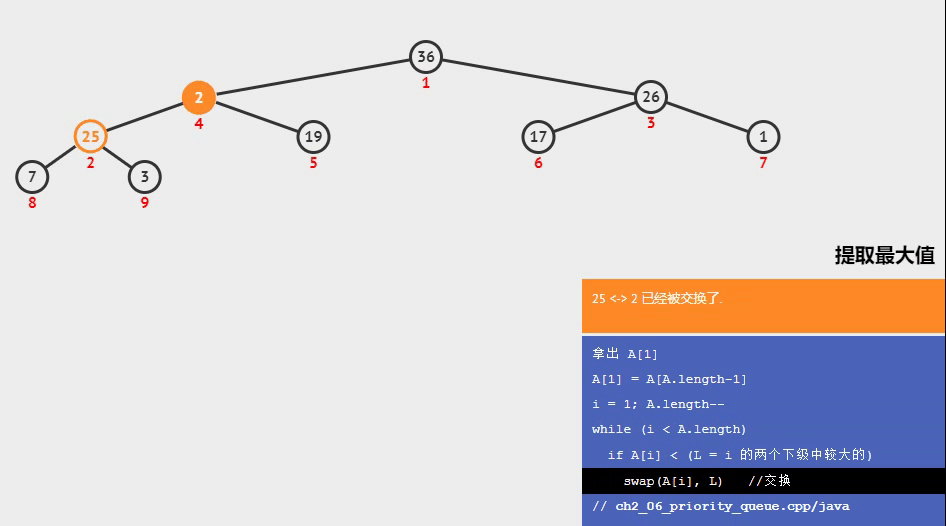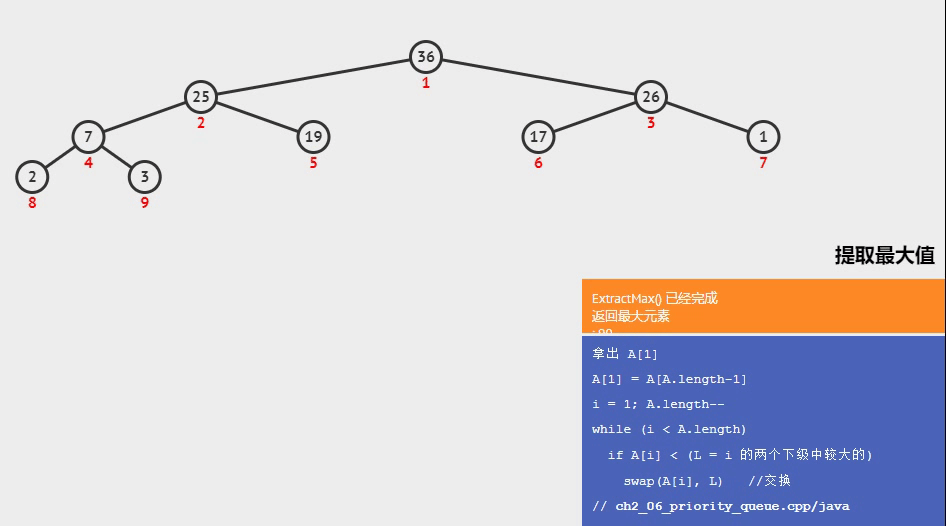
视频截取自可视化算法网站 visualgo.net

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void sink(int k ,int n)//下沉操作
{
    while(2*k<=n)//如果有左孩子，k的左孩子为2k，右孩子为2k+1(前提是根节点标号为1)
    {
        int j = 2*k;
        if(j<n&&A[j]<A[j+1])//如果有右孩子，且左孩子比右孩子小
            j++;//j指向右孩子
        if(A[k]>A[j])//比“较大的孩子”大
            break;  // 已满足堆
        else
            swap(A[k],A[j]);//与较大的孩子交换
        k=j;//k指向交换后的新位置，继续向下比较，一直下沉到叶子
    }
}

构建初始堆

  • 构建初始堆的过程：首先按照完全二叉树顺序构建一棵完全二叉树。然后从最后一个分支节点n/2开始调整堆，依次将序号为 n/2-1,n/2-2,n/2-3……,1的节点执行下沉操作调整为堆。因为从叶子节点没什么可以调整的。没办法下沉了
  • 下面是一个构建初始堆的操作

示例

构建初始堆代码实现
1
2
3
4
5
void CreatHeap (int n)
{
	for(int i = n/2;i>0;i--)
		Sink(i,n);
}

堆排序

  • 构建初始堆之后， 开始进行堆排序。因为最大堆的堆顶是最大的记录，可以将堆顶交换到最后一个元素的位置，然后堆顶执行下沉操作，调整r[1…n-1]为堆即可。重复此过程，直到剩余一个节点，得到有序序列
  • 下面是一个完整的堆排序操作

示例

堆排序代码实现
1
2
3
4
5
6
7
8
9
void HeapSort(int n)//堆排序
{
    CreatHeap(n);
    while(n>1)
    {
        swap(A[1],A[n--]);//堆顶和最后一个记录交换，交换后n-1
        sink(1,n);//堆顶下沉
    }
}

算法分析

时间复杂度

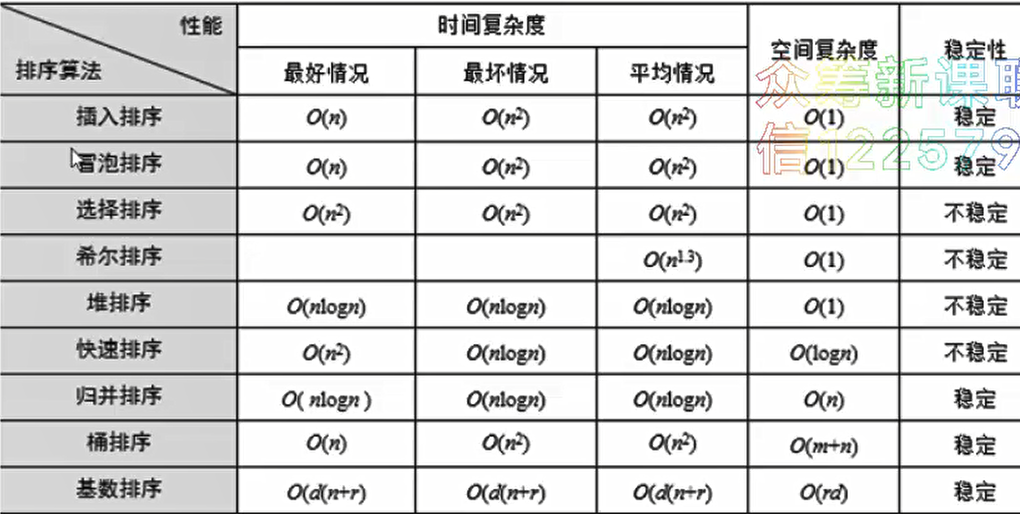
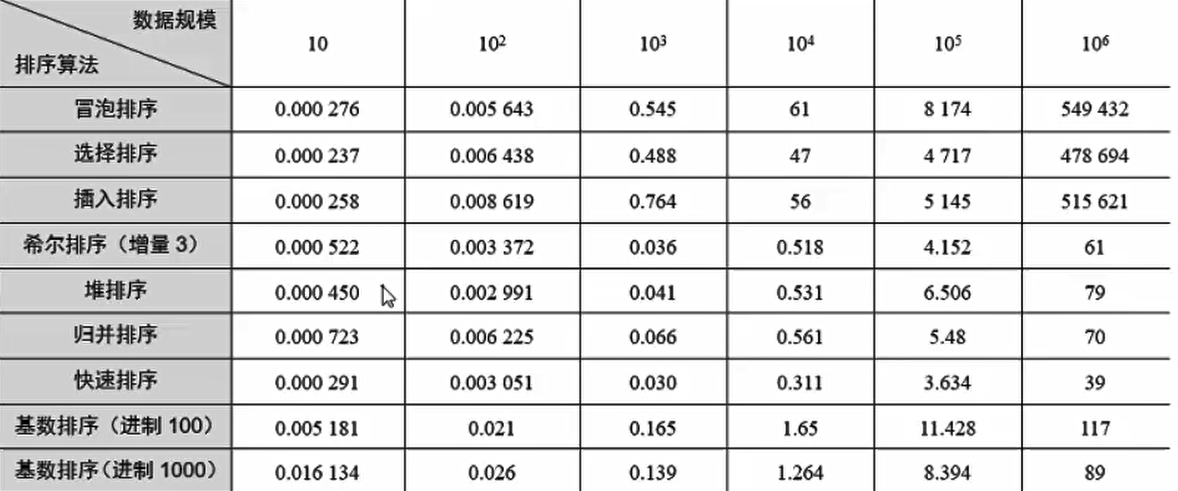
堆排序的运行时间主要耗费在构建初始堆和反复调整堆上。构建初始堆需要从最后一个分支节点（n/2)到第一个节点进行下沉操作，下沉操作最多达到树的深度logn,因此构建初始堆的时间复杂度的上界是O(nlogn)，而实际上这是一个比较大的上界，大多数的分支节点下沉的操作少于logn 。构建n个记录的堆，只需要少于2n次的比较和少于n次的交换，构建初始堆的时间复杂度是线性阶O(n)。堆排序的过程中，每一趟排序需要从堆顶下沉到叶子，下沉操作为树的深度logn ，一共n-1次排序，总的时间复杂度为O(nlogn)

空间复杂度

交换记录时需要一个辅助空间，所以空间复杂度为O(1)

稳定性

对排序的时候多次交换关键字，可能会发生相等关键字排序前后位置不一致的情况，因此堆排序是不稳定的排序方法

示例

示例

代码一览

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include<bits/stdc++.h>
using namespace std;
# define Maxsize 10000
int A[Maxsize];
void sink(int k ,int n)//下沉操作
{
    while(2*k<=n)//如果有左孩子，k的左孩子为2k，右孩子为2k+1
    {
        int j = 2*k;
        if(j<n&&A[j]<A[j+1])//如果有右孩子，且左孩子比右孩子小
            j++;//j指向右孩子
        if(A[k]>A[j])//比“较大的孩子”大
            break;  // 已满足堆
        else
            swap(A[k],A[j]);//与较大的孩子交换
        k=j;//k指向交换后的新位置，继续向下比较，一直下沉到叶子
    }
}
void CreatHeap (int n)
{
    for(int i = n/2;i>0;i--)
        sink(i,n);
}

void print(int n)//输出
{
    cout<<"堆排序的结果"<<endl;
    for(int i=1;i<=n;i++)
        cout<<A[i]<<"  ";
    cout<<endl;
}
void HeapSort(int n)//堆排序
{
    int cnt=n;
    int i = 1;
    CreatHeap(n);
    while(n>1)
    {
        swap(A[1],A[n--]);//堆顶和最后一个记录交换，交换后n-1
        sink(1,n);//堆顶下沉
        print(cnt);
    }
}
int main()
{
    int n ;
    cout<<"请输入数列中的元素个数"<<endl;
    cin>>n;
    cout<<"请依次输入数列中的元素"<<endl;
    for(int i = 1;i<=n;i++)
        cin>>A[i];
    HeapSort(n);
    print(n);
    return 0;
}

优先队列

在算法设计当中，我们经常用到从序列找一个最小值(最大值)的擦欧总，例如最短路径，哈夫曼编码等，都需要用到最小值，如果从序列中顺序查找最小值(最大值)需要$O(n)$ 的时间，而使用优先队列找最小值(最大值)只需要$O(\log n)$ 的时间

优先队列是利用堆来实现的，堆可以看作是一棵完全二叉树的顺序存储结构，在这棵完全二叉树当中，如果每一个节点的值都大于等于左右孩子的值，那么这就被称为最大堆，反之则为最小堆

之前我们已经学过堆了，我们知道如果一个节点的下标为i(从1开始)，那么其左孩子的下表为2i，右孩子的下标为 $2i+1$ ，其双亲的下表为 $i/2$ ，且具有n个节点的完全二叉树的深度为 $\lfloor\log_2n\rfloor+1$

普通的队列是先进先出的，而优先队列与普通队列不同，每次出队时按照优先级顺序出队。例如，最小值出队，优先队列中的记录存储满足堆的定理。

优先队列除了构建初始堆之外，有出队和入队两种常用的操作

算法步骤

  • 构建初始堆
  • 出队：堆顶出队，最后一个记录代替堆顶的位置，重新调整为堆

示例

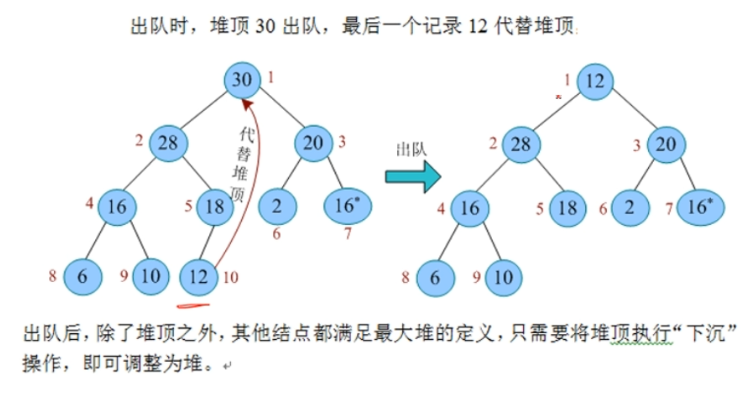
  • 入队：新纪录放入最后一个记录之后，重新调整为堆

算法分析

优先队列是利用堆实现的一种特殊队列，堆是按照完全二叉树顺序存储的，具有 n个结点的完全二叉树的深度为 $\lfloor\log_2n\rfloor+1$ 。出队时，堆顶元素出队，最后一个元素代替堆顶，新的堆顶从根下沉到叶子，最多达到树的深度，时间复杂度为$O(\log n)$ ; 入队时，新元素从叶子上浮到根，最多达到树的深度，时间复杂度也是 $O(\log n)$ 。 优先队列的入队和出队操作间复杂度为$O(\log n)$ ,因此在n个元素的优先队列中找一个最小值(或者最大值)的时间复杂度为$O(\log n)$. 想找到一个最大值就用最大堆，想找到一个最小值就用最小堆。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include <iostream>

using namespace std;

#define maxN 1000
int r[maxN];

void Sink(int k,int n)//下沉操作
{
    while(2*k<=n)//如果有左孩子
    {
        int j=2*k;//j指向左孩子
        if(j<n&&r[j]<r[j+1])//如果有右孩子且左孩子比右孩子小
            j++;    //j指向右孩子
        if(r[k]>=r[j])//比较大的孩子大
            break;    //已满足堆
        else
            swap(r[k],r[j]);//与较大的孩子交换
        k=j;//k指向交换后的新位置，继续向下比较，一直下沉到叶子
    }
}

void Swim(int k)//上浮操作
{
    while(k>1&&r[k]>r[k/2])//如果大于双亲
    {
        swap(r[k],r[k/2]);//与双亲交换
        k=k/2;//k指向交换后的新位置，继续向上比较，一直上浮到根
    }
}

void CreatHeap(int n)//构建初始堆
{
    for(int i=n/2;i>0;i--)//从最后一个分支结点n/2开始下沉调整为堆，直到第一个结点
        Sink(i,n);
}

void push(int n,int x)//入队
{
    r[++n]=x;//n加1后，将新元素放入尾部
    Swim(n);//最后一个元素上浮操作
}

void pop(int n)//出队
{
    cout<<r[1]<<endl;//输出堆顶
    r[1]=r[n--];//最后一个元素代替堆顶，n减1
    Sink(1,n);//堆顶下沉操作
}

int main()
{
    int n,select,x;
    cout << "请输入待排序记录个数：" << endl;
    cin>>n;
    cout<<"请输入n个整数："<<endl;
    for(int i=1;i<=n;i++)
        cin>>r[i];
    CreatHeap(n);//创建初始堆
    while(true)
    {
        cout<<"请选择数字：1.入队；2.出队；0.退出"<<endl;
        cin>>select;
        switch(select)
        {
            case 1:
                cout<<"输入入队元素："<<endl;
                cin>>x;
                push(n,x);//入队
                break;
            case 2:
                pop(n);//出队
                break;
            case 0:
                return 0;
        }
    }
    return 0;
}

练习题

  • 调整时间和树高有关，即$O(h)$ , 在建含有n个元素的堆的时候，关键字的比较总次数不超过4n，时间复杂度为$O(n)$ ,这说明可以在线性时间内，将一个无序数组建成一个堆
-------------本文结束，感谢您的阅读-------------