对弧长的曲线积分

$曲线积分\left\{ \begin{aligned} 对弧长的曲线积分\\对坐标的曲线积分\\积分区域:曲线弧\end{aligned} \right.$

对弧长的曲线积分的概念与性质

如何求曲线形构件的质量

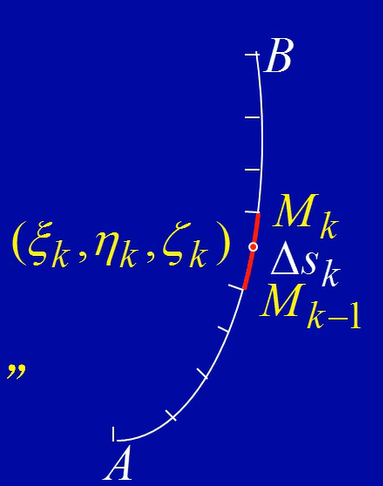
大化小，常代变，近似和，求极限

可得出$M = \lim\limits{\lambda->0}\sum{k=1}^{n}\rho(\xi,\eta,\zeta)\Delta s_k$

定义

空间区域中

设$\Gamma$是空间中一条有限长的光滑曲线，f(x,y,z)是定义在$\Gamma $上的一个优先函数，若通过$\Gamma$的任意分割和对局部的任意取点，下列乘积和式极限，

$\lim\limits{\lambda->0}\sum{k=1}^{n}\rho(\xi,\eta,\zeta)\Delta sk=\int{\Gamma}f(x,y,z)ds$ （s是弧长的微元）都存在，则称这是$f(x,y,z)$在曲线$\Gamma$上对弧长的曲线积分或第一类曲线积分。 $f(x,y,z)$被称为被积函数，$\Gamma$被称为积分弧段。所以曲线形构件的质量就是

$M = \lim\limits{\lambda->0}\sum{k=1}^{n}\rho(\xi,\eta,\zeta)\Delta sk=\int{\Gamma}\rho(x,y,z)ds$

平面积分中

如果L是xOy面上的曲线弧，则定义对弧长的曲线积分为

$\int{\Gamma}f(x,y)ds= \lim\limits{\lambda->0}\sum_{k=1}^nf(\xi,\eta)\Delta s_k$

如果L 是闭曲线，则记为$\oint_Lf(x,y)ds$

思考

$\int_{\Gamma}f(x,y)ds$不是定积分，是曲线积分
若在$\Gamma$上f(x,y)===1,问$\int_{\Gamma}ds$是什么？
- 是该曲线的长度
定积分是否可以看作弧长曲线积分的特例？
- 不是，对弧长的曲线积分要求ds>=0,但是定积分中dx可能为负

性质

$\int{\Gamma}[\alpha f(x,y,z)+\beta g(x,y,z)]ds= \alpha \int{\Gamma}f(x,y,z)ds+\beta\int_{\Gamma}g(x,y,z)ds$
$\int{\Gamma}f(x,y,z)ds= \int{\Gamma1}f(x,y,z)ds+\int{\Gamma_2}f(x,y,z)ds$
设在$\Gamma$上的$f(x,y,z)<=g(x,y,z)$则$\int{\Gamma}f(x,y,z)ds<=\int{\Gamma}g(x,y,z)ds$
$\int_{\Gamma}ds=l(l为弧长的长度)$

对曲线积分的计算

解题步骤

画出被积曲线
把参数带入到f(x,y)中
计算括号内的内容
转化为定积分计算

例题简析

1.$\oint (2xy+3x^2+4y^2)ds ,L$为椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$ ,其周长为a

一般的，如果曲线L对于y轴对称那么

$\int_Lf(x,y)ds=\left\{ \begin{aligned} 2\int_{L1}f(x,y)ds,f(-x,y)=f(x,y)\\0,f(-x,y)=-f(x,y)\end{aligned} \right.$

反之，如果曲线L对于x轴对称那么

$\int_Lf(x,y)ds=\left\{ \begin{aligned} 2\int_{L1}f(x,y)ds,f(x,-y)=f(x,y)\\0,f(x,-y)=-f(x,y)\end{aligned} \right.$

那么原式 = $\oint_L(3x^2+4y^2)ds=\oint_L12ds=12a$

2.$\oint\sqrt{x^2+y^2}ds,L$为圆周$x^2+y^2=ax$

根据上面的结论，我们知道只要求半圆的两倍即可
这里还需要注意，因为这里要求y对于x的导数非常麻烦，所以设参数比较方便
所以设$x(\theta)=\frac{a}{2}+\frac{acos\theta}{2},y(\theta)=\frac{a\sin\theta}{2}$
=$2\int_0^\pi\sqrt{ax(\theta)}\sqrt{x^{‘2}(\theta)+y^{‘2}(\theta)}d\theta$
=$2\cdot\frac{a}{\sqrt{2}}\cdot \frac{a}{2}\int_0^\pi\sqrt{1+cos\theta}d\theta$
=$\frac{a^2}{\sqrt{2}}*\int_0^{\pi}\sqrt2|cos\frac{\theta}{2}|d\theta$
=$a^2*2sin\theta|_0^\pi$

3.$\oint_L x^2 ds 其中L为圆周x^2+y^2+z^2=a^2,x+y+z=0$

根据这种没什么头绪的题目，看起来既不能用参数解决，也不能直接暴力求解。我们就要想到对称。因为这个图像是关于x=y=z轮番对称的，所以$\oint_L x^2 ds=\oint_L y^2 ds=\oint_L z^2 ds$

$=\frac 1 3\int_L(x^2+y^2+z^2)ds=\frac 1 3 \int {a^2}{ds}$

$= \frac 13 a^22\pi a$

对弧长的曲线积分