分治算法和主定理
问题引入
$T(n) = 3T(\frac{n}{2})+O(n)$
那么一直分到最底层,也就是第k层,那么k = logn,这颗树的高度就是logn
那么根据$a^{logb_n}=n^{log_ba} -> O(3^{log_2n})= O(n^{log_23})$
所以第一层复杂度是O(n),公比为 3/2 ,到最后一层复杂度为$(n^{log_23})$
累加得 $O(n^{1.59})$
DC与DP的区别
| DC | DP | |
|---|---|---|
| 子问题的相关性 | 相互独立 | 相互联系 |
| 例子 | 二分搜索,归并排序 | 背包问题,编辑问题 |
| 是否要记笔记 | 不需要 | 需要 |
| 方法 | Top-down | Bottom-up |
Theorem
如果f满足 $f(n) = af(\frac{n}{b})+c$
那么
当 $a>1$时 $ f(n) = O(n^{log_ba})$
当 $a=1$时 $f(n) = O(log_bn)$
那么,如果当 n = b^k 并且 a != 1, k 是一个正整数,$f (n) = C_1n^{log_ba} + C_2;$
where $C_1 = f (1) + c=(a-1) $and $C_2 = -c/(a - 1)$
那么当在Conquer的时候C不是一个常数,又会怎么样呢?
主定理
结论

证明
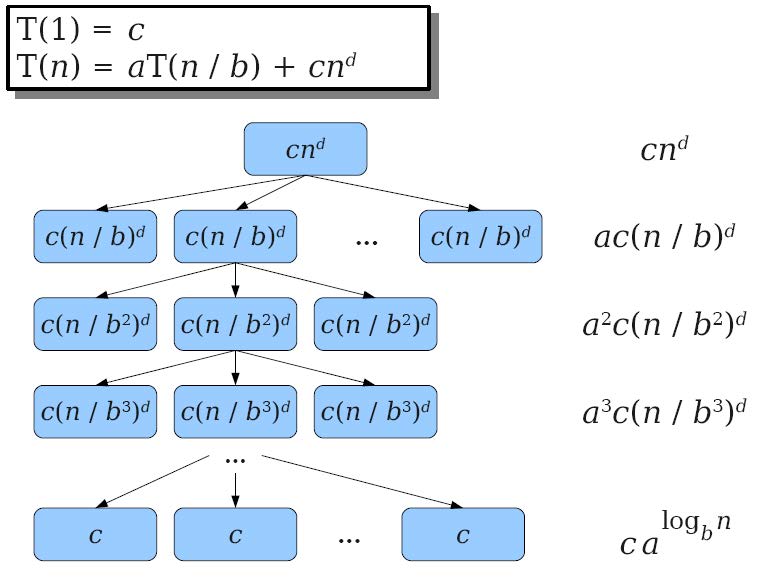
我们可以总结出一个规律
$a^kc(n/b^k)^d = cn^d(a/b^d)^k$
因此
$T(n) = ca^{logbn}+\sum{k=0}^{log_b{n-1}}cn^d(\frac{a}{b^d})^k$
Case1
当$a/b^d = 1$的时候,$a=b^d,d= log_ba$
$T(n) = cn^{logba}+cn^d\sum{k=0}^{log_b{a-1}}(\frac{a}{b^d})^k$
$= cn^d+cn^d\sum_{k=0}^{log_bn-1}1=cn^d+cn^dlog_bn$
$= O(n^dlog_n)$
Case2
当$a/b^d < 1$的时候,$a
$T(n) = cn^{logba}+cn^d\sum{k=0}^{log_b{a-1}}(\frac{a}{b^d})^k$
$< cn^d+cn^d\sum_{k=0}^{log_bn-1}(\frac{a}{b^d})^k=cn^d+cn^dlog_bn$
$< cn^d+cn^d\sum_{k=0}^{\infty}(\frac{a}{b^d})^k=cn^d(1+\frac1{1-a/b^d})$
$=O(n^d)$
Case3
当$a/b^d > 1$的时候,$a>b^d,d< log_ba$
$T(n) = cn^{logba}+cn^d\sum{k=0}^{log_b{a-1}}(\frac{a}{b^d})^k < cn^d + cn^d\frac{(a/b^d)^{log_bn}-1}{(a/b^d)-1}$
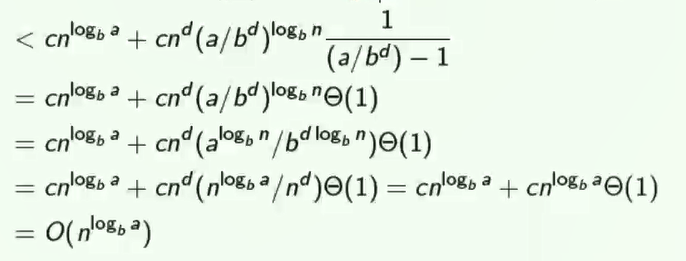
所以这里有几个例子

作业题选
1
Suppose that each person in a group of n people votes for exactly two people from a slate of candidates to fill two positions on a committee. The top two finishers both win positions as long as each receives more than n/2 votes.
a) Devise a divide-and-conquer algorithm that determines whether the two candidates who received the most votes each received at least n/2 votes and, if so, determine who these two candidates are.
b) Use the master theorem to give a big-O estimate for the number of comparisons needed by the algorithm you devised in part (a).
2.
a) Set up a divide-and-conquer recurrence relation for the number of multiplications to compute $x^n$,where x is a real number and n is a positive integer.
b) Use the recurrence relation you find in part (a) to construct a big-O estimate for the number of multiplications used to compute $x^n$ using the recursive algorithm.

现在总共有2n张选票,分成两个子列表,每个子列表有n张选票。我们要选择总票数大于n/2的人选,那么在每个子列表当中,就要选择总票数大于n/4的人选。否则,如果这个人的票数在每个子列表当中,都是小于n/4的,那么加起来必然不可能大于n/2。所以在子列表中最多有3个人的选票可能会超过n/4(如果4个人的话就爆了),这样,每个子列表会选出至多3个候选人。
然后我们在这6个候选人(可重复)中再选出票数大于n/2的最高的两个。那么怎么才能选出票数最高的,当然就是对每个候选人的id,在这整个列表进行遍历,求出他的票数。这样,每个人需要2n次比较,一共12n次。
同样,对于子列表的子列表(每个列表一共n/2张选票),那么我们就要选出每个列表中选票大于n/8的人,这样两个“孙子”列表才可能选出大于n/4的人选递交给第二级列表(总票数为n的列表)。
当我们发现,两个孙子列表提交的6个候选人当中(可重复,且已经统计完成各自票数),top3都是大于n/4的,那么我们就把他们都递交给子列表,否则只返回大于n/4的人,可能为1个,可能为2个,没有的话,就是没有了呗。
同样,我们在两个子列表提交的6个候选人当中(可重复,且已经统计完成各自票数),那么就看头两个是不是有超过n/2张选票,如果超过了的话,那么这两个就是big winner,否则该有几个就是几个
