hashtable

Posted on
Words count in article: 4.5k | Reading time ≈ 19

哈希表

概述

散列表是根据关键字直接进行访问的数据结构。散列表通过散列函数将关键字映射到存储地址，建立了关键字和存储地址之间的一种直接映射关系。这里的存储地址可以实数组下标，索引，内存地址等等

例如：关键字key = (17,24,48,25),散列函数H(key) = key%5,散列函数将关键字映射到存储地址的下标，将关键字存储到散列表的对应位置，如图

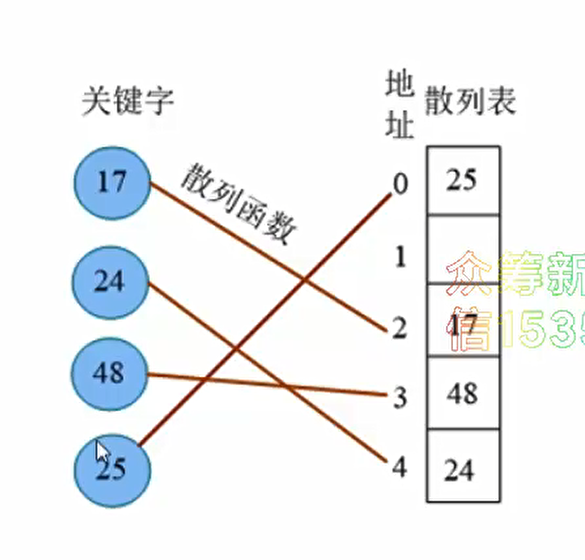
  • 这是理想状态，没有任何重复，这样查找时间就是O(1)的时间。如果冲突的话，也有很多处理方法。这种发生冲突的不同关键词（13和48）为同义词。因此，设计散列函数时应尽量减少冲突，如果冲突无法避免，则需要处理冲突的方法

散列函数

散列函数又称为哈希函数，是将关键字映射到存储地址的函数。记为 hash(key) = Addr 设计遵循为2个原则

  1. 散列函数尽可能简单，能够快速计算出任一关键词的散列地址
  2. 散列函数映射的地址应该均匀分布整个空间，避免聚集，以减少冲突

散列函数设计原则简化为四字箴言：简单，均匀

1.直接定址法

直接提取关键字的某个线性函数作为散列函数，散列函数形式如下：

hash(key) = a*key+b

其中a,b为常数

适用于事先知道关键字，关键字集合不是很大且连续性较好。关键字如果不连续，则造成大量空位，造成空间浪费

例如，学生的学号{601001，601002，…..601006,….601045，…}，那么可以设计散列函数为 H(key) = key-601000

这样可以将学生的学生好直接迎着到存储地址的下标。符合简单均匀的原则

2.除留余数法

  • 除留余数法 是一种最简单最常用的构造散列函数的方法，并且不需要事先知道关键字的分布，假设散列表的表长为m，取一个不大于表长的最大素数p，设计散列函数为：

hash(key) = key%p

为什么要选择p为素数？

  • 为了避免冲突。因为在实际应用中，访问往往具有某种周期性，若周期与p有公共的素因子，则冲突的概率急剧上升。例如手表中的齿轮，两个交合齿轮的齿数最好是互质的，否则出现齿轮磨损绞断的概率很大，因此，发生冲突的概率随着p所含的素因子的增多而迅速增大，素因子越多，冲突也就越多

3.随机数法

  • 随机可以让关键字分布的更均匀一些，因此可以将关键字随机化，然后再使用除留余数法得到存储地址。散列函数为：

hash(key) = rand (key)%p

  • 其中 rand()是C和C++中的随机函数 ，rand(n)表示求0~（n-1）的随机数。p的取值和除留余数法相同

4.数字分析法

  • 数字分析法根据每个数字在各个位上出现的频率，选择平均分布的若干位，作为散列地址。该方法适用于已经直到关键字几何，通过观察分析得到

5.平方取中法

  • 对关键字平方后，按照散列表的大小，取中间的若干位作为散列地址（平方后截取）。适用于事先不知道关键字的分布，且关键码的位数不是很大
  • 例如：散列地址为3位，则关键码10123的散列地址为475

10123^2 = 102475129

6.折叠法

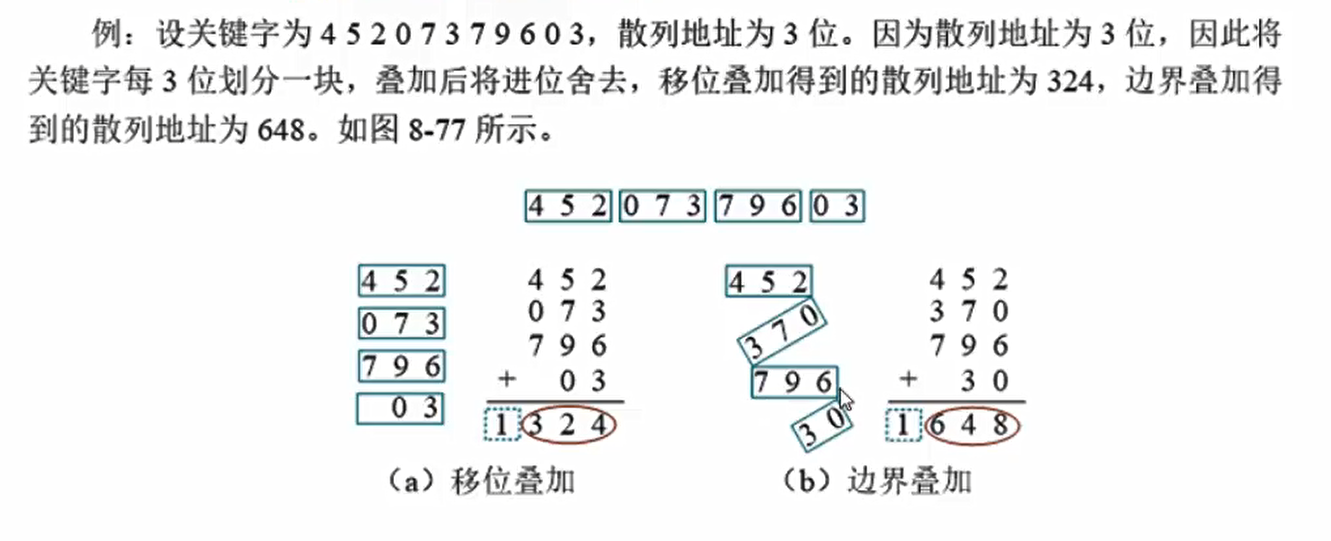
  • 将关键字从左到右分割成位数相等的及部分，将这几部分叠加求和，取后几位作为散列地址。适用于关键字位数很多，事先不知道关键字的分布。折叠法分为移位折叠和边界折叠两种。
    • 移位折叠是将分割后的每一个部分的最低为对齐，然后相加求和
    • 边界折叠如同折纸，将相邻部分沿着边界来回折叠，然后对齐相加

7.基数转换法

例如，将十进制数转为其他的进制表示，例如345转换成九进制表示为423。另外散列函数大多是基于整数的，如果关键字是浮点数，可以将关键字乘以M并四舍五入得到函数，再使用散列函数活着将关键字表示为二进制数然后再使用散列函数,如果关键字是字符，可以将字符串换成R进制的整数，然后再使用散列函数

8.全域散列法

  • 如果对关键字了解不多，可以使用全域散列法。即将多种备选的散列函数放在一个集合H中，在实际应用中，随机选择其中一个作为散列函数。如果任意两个不同的关键字key1!=key2,hash(key1) = hash(key2)的散列函数个数最多是 |H|/m,|H|为集合中散列函数的个数，m为表长，则称H是全域的
  • 一般不常写

冲突处理方式

无论如何设计散列函数，都无法避免冲突问题。如果发生冲突，就需要进行冲突处理。 冲突处理的方法为3种，开放地址法、链地址法、建立公共溢出区

1.开放地址法

开放地址法是在线性存储空间上的解决方案，也称为闭散列。当发生冲突时，采用冲突处理方法在线性存储空间上探测其他的位置

hash'(key) = (hash(key)+d)%m

其中 hash(key)是原散列函数，hash'(key)是探测函数，di是增量序列，m为表长

根据增量序列不同，开放地址法又分为 线性探测，二次探测，随机探测，双倍散列

线性探测法

线性探测法是最简单的开放地址法，线性探测的增量序列为：

$ d_i = 1,2,….m-1 $

例如 ，一组关键字（14,36,42,38,40,15,19,12,51,65,34,25）放到一个长为15的哈希表中，通过visualgo网站的动画我们可以看出线性探测是如何运行的

注意：线性探测法很简单，只要有空间，就一定能探测到位置，但是在处理冲突过程中会出现非同义词之间对同一个散列地址争夺的现象，被称为”堆积“ 。向上面的34一项，探测了6次才找到合适的位置。堆积大大降低了查找效率。因此，要选择好的处理冲突的方法来避免堆积

性能分析：

查找成功的平均查找长度

假设查找的概率均等，(12个关键字，每个关键字查找概率为1/12),查找成功的平均长度等于所有关键字查找成功的比较次数ci乘以查找概率pi的和

当hash(key)=0的时候，如果该空间为空，则比较1次即可确定查找失败。如果该空间非空，关键字又不相等，则继续按照线性探测向后查找。直到遇到空时，才确定查找失败，计算比较次数。类似的，hash(key)=1,….,12也是这样计算的

现在这个哈希表如下：

在最坏的情况下那么平均查找长度就是 （1x3+2x3+3+4+5+6+7+8+11)/13=53/13

二次探测法

二次探测法采用前后跳跃式探测的方法。发生冲突的时候，向前1位探测，向后1位探测，向后 $2^2$ 位探测，向前 $2^2$ 位探测，…..,跳跃式探测来避免堆积。

二次探测的增量序列是：$d_i=1^2,-1^2,2^2,-2^2…k^2,-k^2 $

虽然可以避免出现“堆积”问题，但是缺点是不能探测到散列表上的所有单元，但至少能探测道一半单元

关于二次探测，visualgo上的增量序列是$di=1^2,2^2,3^2..$ 用相同的数据测试时候，会出现探测15次后任然找不到的情况，这时候会报错。可见对于二次探测法也需要科学的增量序列，但是visualgo上的操作也值得借鉴，至少帮我们发现了了一个bug，所以我也展示一下

随机探测法

随即探测法采用伪随机数组进行探测，利用随机化避免堆积，随即探测的增量序列为：

$d_i=伪随机数列$

double hashing

我们来考察最后一个冲突解决方法，双散列（double hashing）。常用的方法是让F（i）= i * hash2( x )，这意思是用第二个散列函数算出x的散列值，然后在距离hash2( x )，2hash2( x )的地方探测。hash2( x )作为关键，必须要合理选取，否则会引起灾难性的后果——各种撞车。这个策略暂时不做过多分析了。

在visualgo上我们也可以看一下模拟情况。这里sec = prime-key%prime

2.链地址法

链地址法又被称为是拉链法。如果不同关键词通过散列函数映射到同一个地址，这些关键字为同义词，将所有的同义词存储在一个线性链表当中，查找，插入，删除操作主要在这个链表中进行，拉链法适用于经常进行插入，删除的情况。

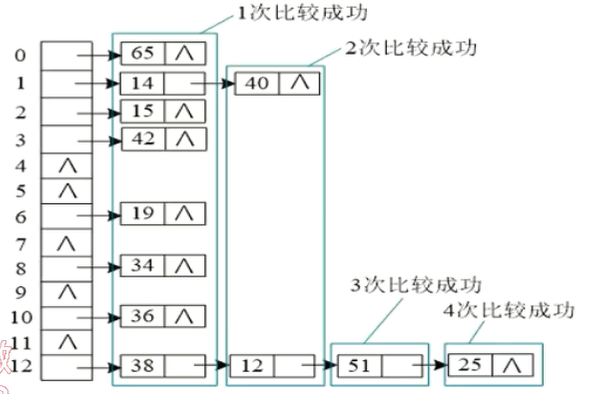
visualgo模拟如下

链地址法求查找失败也非常容易。

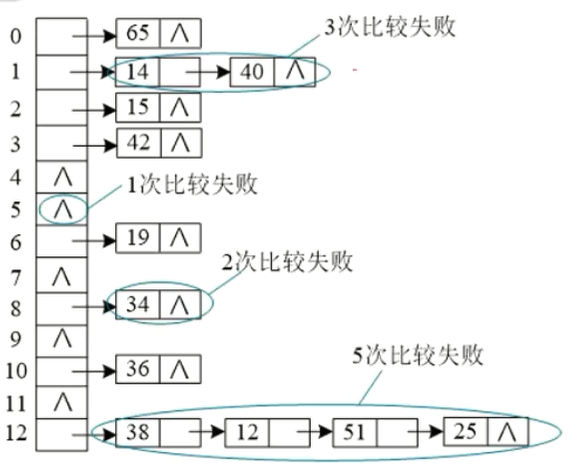
3.建立公共溢出区

除了以上处理冲突方法之外，也可以建立一个公共溢出区，发生冲突的时候，将关键字放入公共溢出区。查找的时候，先根据待查找关键字的散列地址在散列表中查找，如果为空，则查找失败；如果非空且关键字不相等，则到公共溢出区查找，如仍然未找到，则查找失败

总结

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
#include<iostream>
#include<cstring>
#include<cmath>
using namespace std;

#define m 15//哈希表的表长
#define NULLKEY 0//单元为空的标记

int HT[m],HC[m];

int H(int key)//哈希函数
{
	return key%13;
}
//线性探测
int Linedetect(int HT[],int H0,int key,int &cnt)
{
    int Hi;
    for(int i=1;i<m;++i)
    {
        cnt++;
        Hi=(H0+i)%m; //按照线性探测法计算下一个哈希地址Hi
        if(HT[Hi]==NULLKEY)
            return Hi;	//若单元Hi为空，则所查元素不存在
        else if(HT[Hi]==key)
            return Hi; //若单元Hi中元素的关键字为key
    }
    return -1;
}
//二次探测
int Seconddetect(int HT[],int H0,int key,int &cnt)
{
    int Hi;
    for(int i=1;i<=m/2;++i)
    {
        int i1=i*i;
        int i2=-i1;
        cnt++;
        Hi=(H0+i1)%m; //按照线性探测法计算下一个哈希地址Hi
        if(HT[Hi]==NULLKEY)//若单元Hi为空，则所查元素不存在
            return Hi;
        else if(HT[Hi]==key)//若单元Hi中元素的关键字为key
            return Hi;
        cnt++;
        Hi=(H0+i2)%m; //按照线性探测法计算下一个哈希地址Hi
        if(Hi<0)
            Hi+=m;
        if(HT[Hi]==NULLKEY)//若单元Hi为空，则所查元素不存在
            return Hi;
        else if(HT[Hi]==key)//若单元Hi中元素的关键字为key
            return Hi;
    }
    return -1;
}

int SearchHash(int HT[],int key)
{
    //在哈希表HT中查找关键字为key的元素，若查找成功，返回哈希表的单元标号，否则返回-1
    int H0=H(key); //根据哈希函数H（key）计算哈希地址
    int Hi,cnt=1;
    if(HT[H0]==NULLKEY)//若单元H0为空，则所查元素不存在
        return -1;
    else if(HT[H0]==key)//若单元H0中元素的关键字为key，则查找成功
        {
            cout<<"查找成功，比较次数："<<cnt<<endl;
            return H0;
        }
        else
        {
            Hi=Linedetect(HT,H0,key,cnt);
            if(HT[Hi]==key)//若单元Hi中元素的关键字为key，则查找成功
            {
                cout<<"查找成功，比较次数: "<<cnt<<endl;
                return Hi;
            }
            else
                return -1;	//若单元Hi为空，则所查元素不存在
        }
}

bool InsertHash(int HT[],int key)
{
    int H0=H(key); //根据哈希函数H（key）计算哈希地址
    int Hi=-1,cnt=1;
    if(HT[H0]==NULLKEY)
    {
        HC[H0]=1;//统计比较次数
        HT[H0]=key;	//若单元H0为空，放入
        return 1;
    }
    else
    {
        Hi=Linedetect(HT,H0,key,cnt);//线性探测
        //Hi=Seconddetect(HT,H0,key,cnt);//二次探测
        if((Hi!=-1)&&(HT[Hi]==NULLKEY))
        {
            HC[Hi]=cnt;
            HT[Hi]=key;//若单元Hi为空，放入
            return 1;
        }
    }
    return 0;
}

void print(int HT[])
{
    for(int i=0;i<m;i++)
        cout<<HT[i]<<"\t";
    cout<<endl;
}

int main()
{
	int x;
	memset(HT,0,sizeof(HT));
	memset(HC,0,sizeof(HC));
	print(HT);
	cout<<"输入12个关键字，存入哈希表中："<<endl;
	for(int i=0;i<12;i++)
	{
		cin>>x;
		if(!InsertHash(HT,x))
		{
		    cout<<"创建哈希表失败！"<<endl;
		    return 0;
		}
	}
	cout<<"输出哈希表："<<endl;
	print(HT);
	print(HC);
	cout<<"输入要查找的关键字"<<endl;
	cin>>x;
	int result=SearchHash(HT,x);
	if(result!=-1)
		cout<<"在第"<<result+1<<"位置找到"<<endl;
	else
		cout<<"未找到"<<endl;
    return 0;
}

//14 36 42 38 40 15 19 12 51 65 34 25

例题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include<bits/stdc++.h>
#include <hash_map>

using namespace std;
using namespace __gnu_cxx;
const int hash_size = 10;
class hash_funcion{
public:
    size_t operator()(const int &key) const
    {
        return size_t(key%hash_size);
    }
};
class key_compare{
public:
    bool operator()(const int &key1, const int &key2)const {
        return  key1==key2;
    }
};
int main()
{
   hash_map<int ,int,hash_funcion,key_compare>myhash;
   int k;
   cin>>k;
   int numbers[k];
   for(int i = 0 ;i<k;i++)
    {
       cin>>numbers[i];
    }
    int target = 0;
   cin>> target;
   for(int i = 0;i<k;i++)
    {
      myhash[numbers[i]] = i+1;
    }
   int num = 0;
   for(int i = 0;i<k;i++)
    {
       int current_num = numbers[i];
       int current_pos = i+1;
       hash_map<int,int,hash_funcion,key_compare>::iterator it = myhash.find(target-current_num);
       if( it!= myhash.end())
        {
            if(it->second>current_pos){
                num++;
                cout<<"["<<current_pos<<","<<it->second<<"]"<<endl;
            }
        }
    }
    if(num==0)
    {
        cout<<"None"<<endl;
    }
   return 0;
}

自己实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
#include<bits/stdc++.h>
using namespace std;
enum Error_code{not_present,overflow,duplicate_error,success};
const int hash_size =10;
//key 这个类来保存关键字
class Key{
    int key;
public:
    Key (int x = 0){
        this->key = x;
    }
    int the_key() const;
};

int Key::the_key() const {
    return key;
}
//record 就是下标
class Record{
private:
    int key;
    int other;
public:
    operator Key(){
        return Key(this->key);
    }
    Record (int x= 0,int y = 0)
    {
        this->key = x;
        this->other = y;
    }
    int the_key() const ;
    int the_other() const ;
};
int Record::the_key() const {
    return key;
}

int Record::the_other() const {
    return other;
}
//重载两个运算符
bool operator !=(const Record &x, const Record &y)
{
    return x.the_key() != y.the_key();
}
bool operator ==(const Record &x, const Record &y)
{
    return x.the_key() == y.the_key();
}

int hash_fun(const Record &new_entry)
{
    return new_entry.the_key() %hash_size;
}
int hash_fun(const Key &new_entry)
{
    return new_entry.the_key() %hash_size;
}

class Hash_table{
public:
    void clear();
    Error_code insert(const Record &new_entry);
    Error_code retrieve(const Key &target, Record &found) const ;
private:
    Record table[hash_size];
};
Error_code Hash_table::retrieve(const Key &target,Record &found) const{
    int probe_count,increment,probe;
    probe = hash_fun(target);
    probe_count = 0;
    increment = 1;
    while(table[probe]!=0&&table[probe].the_key()!=target.the_key()&&probe_count<(hash_size+1)/2)
    {
        probe_count++;
        probe = (probe+increment)%hash_size;
        increment+=2;
    }
    if(table[probe].the_key() == target.the_key()){
        found = table[probe];
        return  success;
    } else return not_present;
}

Error_code Hash_table::insert(const Record &new_entry) {
    Error_code result = success;
    int probe_count,increment,probe;
    probe = hash_fun(new_entry);
    probe_count = 0;increment = 1;
    while(table[probe]!= 0&&table[probe]!=-1&&probe_count<(hash_size+1)/2){
        probe_count++;
        probe = (probe+increment)%hash_size;
        increment+=2;
    }
    if(table[probe]==0) table[probe] = new_entry;
    if(table[probe]== -1) table[probe] = new_entry;
    else result = overflow;
    return result;

}

int main()
{
    int k;
    cin>>k;
    int numbers[k];
    for(int i = 0 ;i<k;i++)
    {
        cin>>numbers[i];
    }
    int target = 0;
    cin>> target;
    Hash_table myhash;
    for(int i = 0;i<k;i++)
    {
        myhash.insert(Record(numbers[i],i+1));
    }
    int num = 0;
    for(int i = 0;i<k;i++)
    {
        int current_num = numbers[i];
        int current_pos = i+1;
        Record record;
        Error_code result = myhash.retrieve(Key(target-current_num),record);
            if( result==success&&record.the_other()>current_pos)
            {
                    num++;
                    cout<<"["<<current_pos<<","<<record.the_other()<<"]"<<endl;
            }
    }
    if(num==0)
    {
        cout<<"None"<<endl;
    }
}

练习

计算查找成功的平均比较次数和查找失败的平均比较次数

  1. 现有长度为7，初始为空的散列表 HT，散列函数$H(k) = k%7$ ，用线性探测再散列法解决冲突，将关键字22、43、15依次插入HT之后，查找成功的平均查找长度是：

注意，查找成功的平均查找长度，是只要算到找到为止(包含最后找到的那次) 的对比次数，这里，22%7=43%7=15%7 = 1，因此，在查找时

  1. 现有长度为11且初始为空的散列表HT，散列函数是$H(key) = key\%7$ ，用线性探查法解决冲突，将关键字序列：87、40、30、6、11、22、98、20依次插入HT之后，HT查找失败 的平均查找长度为：
0 1 2 3 4 5 6 7 8 9 10
98 22 30 87 11 40 6 20

由于$H(key) = 0 \sim 6$ 查找失败可能对应的地址有7个，对于计算地址为0的关键字 key0， 只有比较完0~8 号地址之后，才能确定该关键字不在表中，比较次数为9.

以此类推， key1比较次数为8，….. ， key6比较次数为3

因此 $ASL = (9+8+7+6+5+4+3)/7=6$

对于散列表也是这样，查找失败的ASL的计算方法 = $\sum_{i=0}^{n-1} \text{[num(i)+1]}$ n为散列函数%的值，$num(i)$ 即余数为i的列表中的关键字个数

一些结论

  • 散列表中，查找的平均查找长度与表长无关
  • 在开放定址的情形下，不能随便删除散列表中的某个元素，否则可能会导致搜索路径被中断。因此，通常的做法是在要删除的地方做删除标记，而不是直接删除
-------------本文结束，感谢您的阅读-------------