计数原理
- Counting principles
+ Product rule
+ Sum rule
+ Subtraction rule
+ Division rule
- Permutations
- Combinations
- 定义如下

我们拿到题目要看看到底是要求我们用排列做还是组合做,可否重复?然后再对应相同的公式
Distributing Objects into Boxes
这个系列有点搞脑子的,就是把一些物体放到一些箱子里去
Distinguishable Objects and Distinguishable Boxes
- 要我们把可分辨的物体放到可分辨的箱子里去,该如何解决?
问题引入:
I have 9 different presents. I want to give them to 3 students: A, B,and C. I want to give each student 3 presents. In how many ways can I do it?
我们可以这样看,有一张1-9的表格,填A,B,C
| Presents | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Children | A | B | A | B | C | B | C | A | C |
所以ABC可以在这九个位置随便排,但是相同的ABC交换的时候,并不会多出一种情况,所以这就要把他们都除掉,因为ABC每个只能出现3个,所以答案就是
$\frac{9!}{3!3!3!}$
Generalization
The number of ways to distribute n distinguishable objects into k distinguishable boxes so that $n_i$ objects are placed into box i , i = 1, 2,….. k, equals
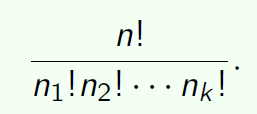
Indistinguishable Objects and Distinguishable Boxes
- 要我们把不可分辨的物体放到可分辨的箱子里去,该如何解决?
问题引入:How many ways are there to place 10 indistinguishable balls into eight distinguishable bins?
模型就是隔板法。我们要把r个不可辨别放到n个箱子里去。就是说我们要用n-1块挡板把r个物体分成n个部分,每个部分可以为0。 如果单单在r个物体插入n-1块挡板的话呢,就是C(r-1,n-1)但是这样显然无法满足我每个部分可以为0的情况,因为这是每个盒子中必须有物体的计算公式。因此我们还要把隔板为0的部分计算在内,所以公式是C(n-1+r,n-1)。也就是说一个一块长为n-1+r的区域,你挑选n-1个放置隔板剩余的放物体。
- 那如果说我对盒子中的物体有要求,又该如何解决呢?
问题引入2:I have 9 indentical coins. I want to give them to 3 students: A, B, and C. In how many ways can I do it so that each student gets at least one coin?
这个问题,就是上面我们讨论的问题了,也就是说当每个盒子中的物体都至少为1的时候呢,相当于在r个球之间的r-1个空隙选择n-1个位置放置我们的隔板,所以C(r-1,n-1)就是最后的答案,在这里,答案是C(8,2)
这个问题,也可以这样考虑,既然说我们每个人都要拿到至少一个硬币的话,那么我们不妨先让每一个人都拿一个硬币。然后再按照盒子可为空的方法进行计算。比如这里一共有9个硬币,先让每个人都拿一个,那么还剩下6个硬币。随后,我们根据C(n-1+r,n—1)来进行计算得到的答案是C(3-1+6,3-1)=C(8,2)可见答案相同
Distinguishable Objects and Indistinguishable Boxes
- 那么如果把可以分辨的物体,放到不可分辨的盒子中的情况呢?
问题引入:How many ways are there to put four different employees into three
indistinguishable offices, when each offce can contain any number of employees?

形如这样,我也不太好总结
Indistinguishable Objects and Indistinguishable
- 那么如果两者都是不可分辨的话,该怎么办呢?
问题引入:How many ways are there to pack six copies of the same book into four identical boxes, where a box can contain as many as six books?
呵呵,没有啥好办法,自己数数8

作业剪影
第一题
A bagel shop has onion bagels, poppy seed bagels, egg bagels, salty bagels, pumpernickel bagels, sesame seed bagels, raisin bagels, and plain bagels. How many ways are there to choose
a) six bagels? $C(6+8-1,6)$
因为有8给种类的Bagels,从中选择6个,显然是可重复的组合数,我们选择 $C(n+r-1,r)$ 这一个公式来计算。
b) a dozen bagels? $C(8+12-1,12)$
8个种类的Bagels 可重复选择,选一打12个,我们使用 $C(n+r-1 ,r)$ 来计算
c) two dozen bagels? $C(8+24-1,24)$
d) a dozen bagels with at least one of each kind? $C(8+12-8-1,4)$
要求一打Bagels中所有的种类都至少有一个,那么我们先把所有种类都选择一遍,所以现在等于是在8种bagels种选择4个,可重复。
e) a dozen bagels with at least three egg bagels and no more than two salty bagels?
要求一打bagels种至少有三个 egg bagels 和不超过两个的 salty bagels,那么就进行分类讨论
$C(7+12-3-0-1,9)+C(7+12-3-1-1,8)+C(7+12-3-2-1,7)$

第二题
2.How many different combinations of pennies, nickels, dimes, quarters, and half dollars can a piggy bank contain if it has 20 coins in it?
这是典型的Indistinguishable Objects into Distinguishable Boxes 的题目。我们要把20个无差别的硬币放到5个标号为pennies、nickelsdimes盒子。所以
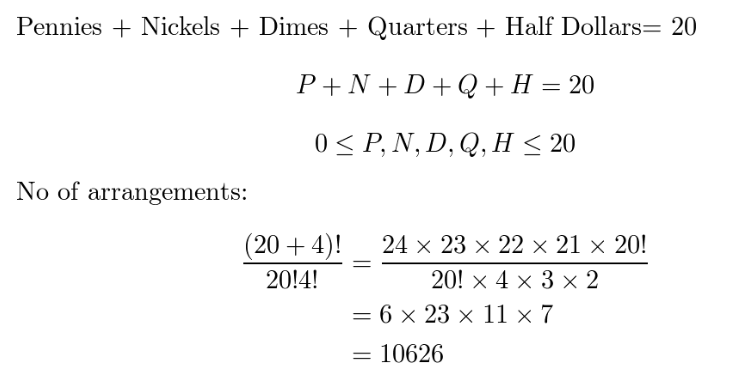
第三题
How many solutions are there to the equation
$x1 + x2 + x3 + x4 + x5 = 21$,
where xi , i = 1, 2, 3, 4, 5, is a nonnegative integer sucht hat
a) x1 ≥ 1?
b) xi ≥ 2 for i = 1, 2, 3, 4, 5?
c) 0 ≤ x1 ≤ 10?
对于$x_1$ 的限定条件,我们可以采取这种思路: 首先去掉条件,单纯计算 $x1 + x2 + x3 + x4 + x5 = 21$ 有几种可取情况。 其次反向计算出不满足调浅的情况,再用总数减去不满足的情况得到答案。

d) 0 ≤ x1 ≤ 3, 1 ≤ x2 < 4, and x3 ≥ 15?



对于这种题目,我们可以反向相减法来解决。比如要求 0 ≤ x1 ≤ 3, 1 ≤ x2 < 4, and x3 ≥ 15?,我们就先求$x_2\geq1,x_3\geq 15$ 然后再求 $x_1\geq 1 x_2\geq 4,x_3\geq 15$ 的,最后求 $x_2\geq4,x_3\geq 15$ 的后两者是不符合要求的,减去即可
因为不存在 $x_1\geq4,x_2\geq 4,x_3\geq 15$ 的情况,所以$x_2\geq4,x_3\geq 15$和$x_2\geq1,x_3\geq 15$并没有并集,所以不需要再加上什么东西。
每次只能控制一个变量!看清是小于还是小于等于
或者直接用生成函数来求解,也是可以的
第四题(练习)
How many solutions are there to the equation
x1 + x2 + x3 + x4 + x5 + x6 = 29,
where xi , i = 1, 2, 3, 4, 5, 6, is a nonnegative integer such that
a) xi > 1 for i = 1, 2, 3, 4, 5, 6?
b) x1 ≥ 1, x2 ≥ 2, x3 ≥ 3, x4 ≥ 4, x5 > 5, and x6 ≥ 6?
c) x1 ≤ 5?
d) x1 < 8 and x2 > 8?
对于d,我们先求 $x_1\geq 0, x_2\geq 9$ 的情况,为 $C(6+29-9-1,29-9)$
然后求 $x_1\geq 8$(这是重点,千万别写 $x_1\geq 9$!!!!!),$x_2\geq 9$ 的情况,为 $C(6+29-9-8-1,29-9-8)$
最后两者相减得到答案。
生成排列
详见博文生成排列代码实现