格林公式
区域D的分类
单连通区域(无洞区域)
多连通区域(有洞区域)
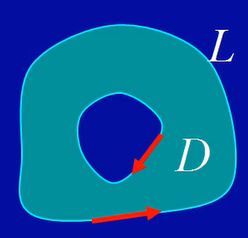
域D边界L的正向:域的内部靠左,这两个方向都是正向
定理
设区域D是由分段光滑正向曲线L围成,函数P(x,y),Q(x,y)在D上具有连续的一阶偏导数。则有
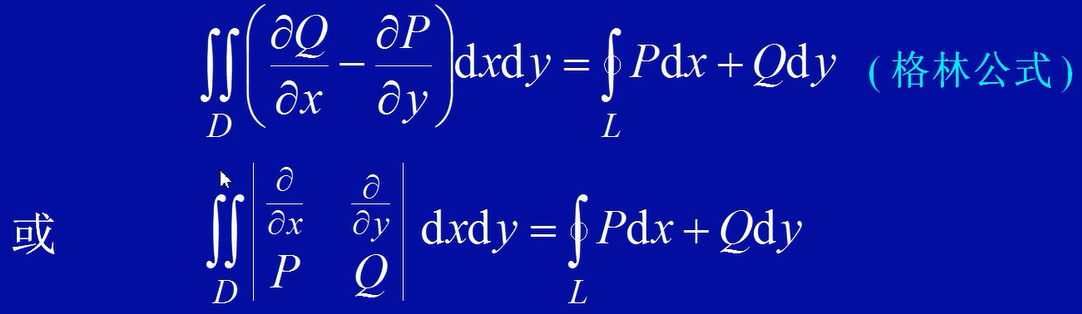
推论
根据格林公式:正向闭曲线L所围成的区域D的面积
$A = \frac{1}{2}\oint_Lxdy-ydx$
注意,格林公式的P跟dx,所以上面的P是-y,Q是x
例子
椭圆 $L:x=acos\theta,y=bsin\theta ,(0\leq\theta\leq2\pi)$所围成的面积
$A = \frac 12\oint_Lxdy-ydx=\frac 12\int_0^{2\pi}(abcos^2\theta+absin^2\theta)d\theta=\pi ab$
解题步骤
- 先写明 P=XXX,Q=XXX
- 判断是正向还是逆向,逆向加上负号
- 计算 偏导数
- 利用格林公式转换
习题
正向格林公式

逆向格林公式:

这道题目,需要用逆向思维,把现在的函数倒退成未进行格林公式变形时的积分。然后还需要转几个弯。利用坐标的曲线积分求解的时候,需要判断出$\vec{AB},\vec{BO}$都为0,只需要求$\vec{OA}$即可
分类讨论:


平面上曲线积分与路径无关的等价条件
定理
设D 是单连通区域,函数P(x,y),Q(x,y)在D内具有异界连续偏导数,则下列四个条件等价
- 沿D中任意光滑闭曲线L,由$\oint_LPdx+Qdy=0$
- 对D中任一分段光滑曲线L,曲线积分$\int_LPdx+Qdy$与路径无关,只与起止点有关
- Pdx+Qdy在D内是某一函数$u(x,y)$的全微分,$du(x,y)=Pdx+Qdy$
- 在D内每一点都有$\frac{\delta P}{\delta y}=\frac{\delta Q}{\delta x}$
说明
根据定理,若某区域D内 $\frac{\delta P}{\delta y}=\frac{\delta Q}{\delta x}$
- 计算曲线积分时,可选择方便的积分路径,一般是直线。
- 求曲线积分时,可利用格林公式简化计算,若积分路径不是闭曲线,可以添加辅助线


例题
例一

例二+例三+例四



- 注意,一般让你求全微分原函数地,都是从(0,0)但要符合条件到x,y,这样会方便很多
- $\int_L\frac{(3y-x)dx+(y-3x)dy}{(x+y)^3}$其中L是由点$A(\frac{\pi}{2},0)$沿着曲线 $y = \frac{\pi}{2}cosx$到点$B(0,\frac{\pi}{2})$的弧段
- 首先确定P和Q,判断是不是$\frac{\delta P}{\delta y}=\frac{\delta Q}{\delta x}$
- 知道他们相等后,我们选择最简单的路径,也就是AB直线,然后带入
- 积分限就是x1->x2,因为是对x积分。然后把y带入求积分
- 验证$e^x[e^y(x-y+2)+y]dx+e^x[e^y(x-y)+1]dy$是某个函数u(x,y)的全微分,并求出这样一个u(x,y)
- 首先确定P和Q,判断是不是$\frac{\delta P}{\delta y}=\frac{\delta Q}{\delta x}$
- 知道他们相等
- $u(x,y)=\int_{(0,0)}^{(x,y)}e^x[e^y(x-y+2)+y]dx+e^x[e^y(x-y)+1]dy$
- $=\int_0^x(x+2)e^xdx+\int_0^y(xe^xe^y-e^x)dy$
- 然后就可以求出原函数了
题形汇总+注意点提示
1.利用格林公式,求下列曲线积分
- 循规蹈矩,不要跳步
- 找到Pdx和Qdy
- 计算$\frac{\delta P}{\delta y}$和$\frac{\delta Q}{\delta x}$
- 把曲线积分化成二重积分进行计算
注意点:
- 对面积$A = \frac{1}{2}\oint_Lxdy-ydx$ 要敏感
- 如果区域$D_{xy}$是包含原点的,一定要挖出一块区域,再减去这块包含原点的区域的边界的曲线积分
- 比如书本练习题2-10
2.全微分怎么找呢?
- 首先判断是否满足是否$\frac{\delta P}{\delta y}=\frac{\delta Q}{\delta x}$
- 先取一个定点,然后取一个动点,这里是(0,0),和(x,y)
- 因为积分结果与路径无关,基本所有的题目都可以这样取路径(0,0)到(x,0)然后(x,0)到(x,y)
- 所以说先从(0,0)到(x,0)的时候,y = 0,dy=0,带入,那么第一段就等于0
- 再从(x,0)到(x,y)的时候,x是一个常数了,所以dx = 0所以第二段的Pdx就等于0 ,剩下的相当于对dy进行积分操作
- 注意,当 分母 $|_{(0,0)}=0$的时候,就不能取原点了!换成(1,0)试试
3.验证下列曲线积分与路径无关,并计算其值
- 首先判断是否满足是否$\frac{\delta P}{\delta y}=\frac{\delta Q}{\delta x}$
- 和全微分的计算方法差不多,不过这里$\int_{(x_1,y_1)}^{(x_2,y_2)}$ 可以是任意值
- 所以我们还是要走一个矩形,固定y走x ,然后固定x走y
- 分别带入求解
4.确定闭曲线C使曲线积分达到最大值
- 首先利用格林公式把曲线积分化成二重积分的形式
- 要让二重积分达到最大值,D应包含所有使被积函数大于0的点。
- 比如$\iint_D[1-2x^2-y^2]dxdy$ ,这时候D应由椭圆$2x^2+y^2=1$ 所围成的闭区域。这就是说,当C为取逆时针方向的椭圆$2x^2+y^2=1$ 时,所给的曲线积分达到最大值
- 注意,曲线积分逆时针的时候取正,如果题目要求最小值,那么应该取顺时针。
课本练习




第十题非常经典,因为当包含原点的时候,分母为0,所以这一点,是没有导数的,我们要设计一个区域把他挖掉,又能刚好把分母分子能够相消


