对面积的曲面积分

概念和性质

引例

设曲面形构件具有连续面密度$\rho(x,y,z)$，求质量M

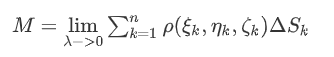
定义

其中，$\lambda$表示n小块曲面直径的最大值（曲面的直径为其上任意两点间距离的最大者）

性质

对面积的曲面积分与对弧长的曲线积分性质类似

积分的存在性：若f(x,y,z)在光滑曲面$\Sigma$ 上连续。则对面积的曲面积分存在
对积分域的可加性。若$\Sigma$是分片光滑的，例如分成两片光滑曲面$\Sigma_1,\Sigma_2$,则有

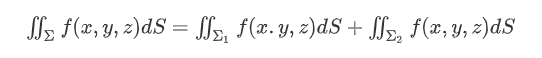
对面积的曲面积分的计算法

定理：

说明1:

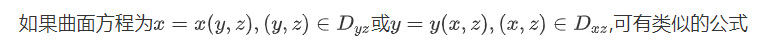
说明2：

若曲面为参数方程，只要求出在参数意义下的dS表达式，也可以将对面积的曲面积分转化为对参数的二重积分

例题

1

需要注意的是，如果说$\Sigma$是球面$x^2+y^2+z^2 = a^2$被平行平面截出$z=\pm h$的上下两部分，则

$\iint_{\Sigma}\frac{dS}{z}=0$

$\iint_{\Sigma}\frac{dS}{|z|}=4\pi a ln\frac{a}{h}$

2

3 4..可以直接转换成球面积分柱面积分，而不用转换成二重积分

5.可以直接转换成球面积分柱面积分，而不用转换成二重积分

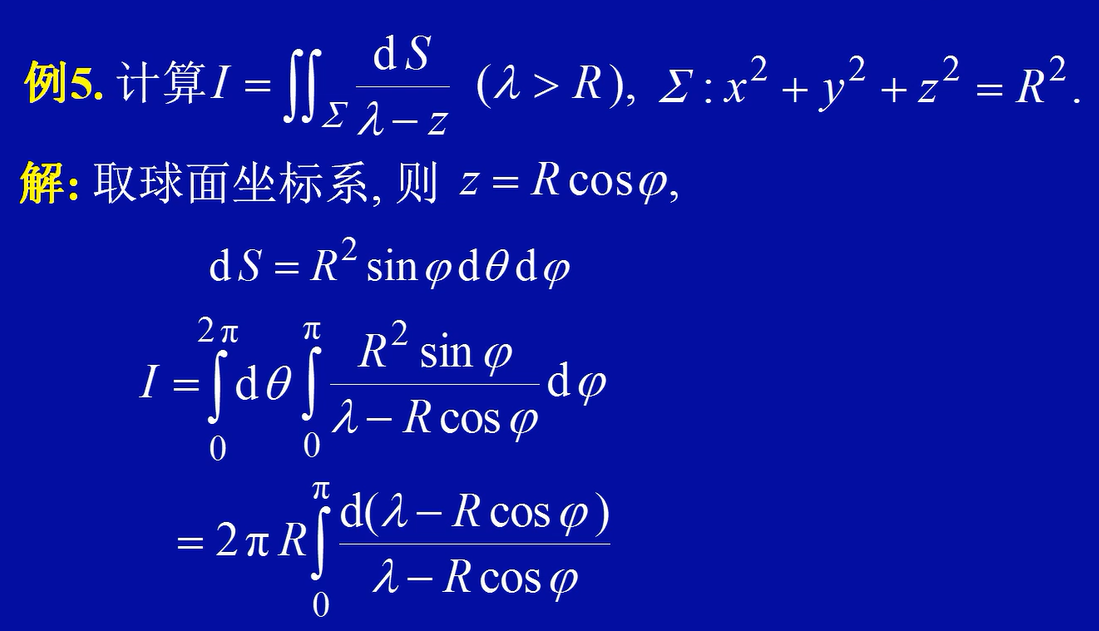
6.

$\iint_{\Sigma}(ax+by+cz+d)^2 dS$，其中$\Sigma$是球面$x^2+y^2+z^2 = R^2$

拿到这种被积函数比较复杂的，先判断有没有对称性，把能消除的都消除

比如 $2abxy,2bcyz,2axd$这种的项，都是f(-x,y)=-f(x,y)类型的奇函数，所以直接变0即可

最后就转化成 $\iint(a^2x^2+b^2y^2+c^2z^2+d^2)dS$

这里还要转一个弯,那就是对球面来说

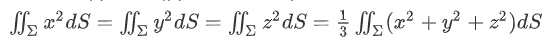
所以说，把他们拆分开，系数提取出来，最后就得到了

$=\frac{a^2+b^2+c^2}{3}4\pi R^4+d^24\pi R^2$

题型+注意点

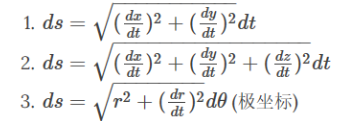
$dS = R^2sin\varphi d\theta d\varphi$
能不能用柱坐标求解： $dS = dzd\theta$
和曲线积分 $\oint _{L} dS = $ 线长度一样

$\iint _{\Sigma} dS=$ 曲面的面积。

要注意$\Sigma$到底代表了什么，是整个立体的表面，还是不包括顶部的，这点非常重要

题型：

求球面或者抛物面的质量问题 $m=\iint\rho(x,y,z)dS$

然后设参数，变量代换求解

解法

拿到题目，先画曲面图像
看看有没有对称性能不能归零合一比如对于轮换对称的曲面
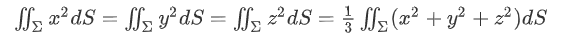
看看能不能利用球面坐标求解 $dS = R^2sin\varphi d\theta d\varphi$, 能不能用柱坐标求解： $dS = dzd\theta$
然后解出z=z(x,y)
求出$Dxy $ , 就是把曲面投影到$xOy$平面上来
把$z=z(x,y)$和z对x,对y的偏导数带入公式
先转换成二重积分，然后根据$Dxy$ 求解二重积分