离散概率

Posted on
Words count in article: 1.3k | Reading time ≈ 6

离散概率

概念

运算

加

  • if $A\cap B = \emptyset$
  • $P(A\cup B) = P(A)+P(B)$

Theorem

Let E1 and E2 be events in the sample space $\Omega$.Then

$P(E_1\cup E_2)= P(E_1)+P(E_2)-P(E1\cap E2)$

证明：

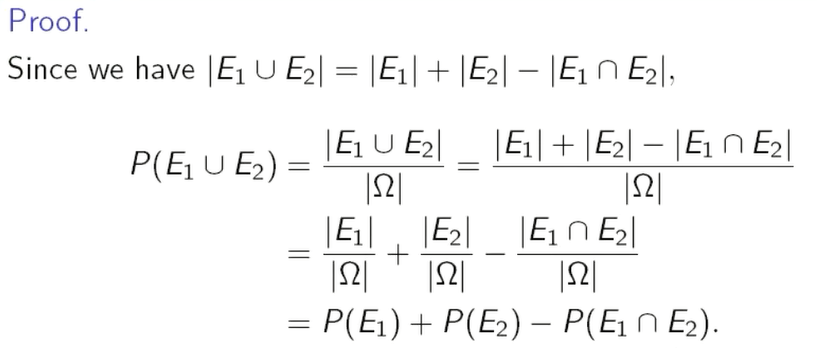
但这个证明不是很严谨，默认这是均匀分布的，才能够这么写

应该这么写

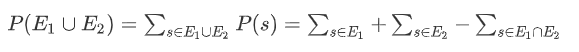
推论

  • if $E_i\cap E_j=\emptyset $ for $\forall i,j$ then
  • $P(\bigcup{i=0}^{\infty})=\sum{i=1}^{\infty}P(E_i)$
  • 三个事件发生的概率—— 容斥原理

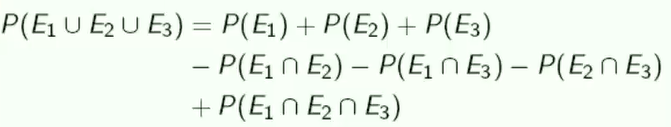
减

  • $A\subset \Omega$

  • $P(\overline A)=P(\Omega)-P(A)=1-P(A)$

证明

分清楚对立事件和互斥事件。对立事件是：不是你就是我，互斥时间是：两者没有交集

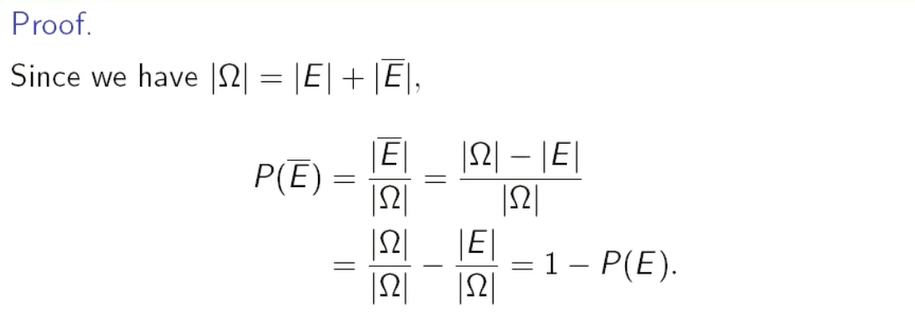
例子： 正难则反

乘

  • 如果A和B是相互独立的，那么
  • $P(A\cap B)=P(A)\cdot P(B)$

  • $P(A)=P(B)=P(C) = 0.5$
  • $P(A\cap B) = P(A\cap C) = P(B\cap C) = 0.25$ 两两独立
  • $P(A\cap B\cap C) = 0.25$ 这不是相互独立
  • 所以这里有个重要的概念——独立
  • 一类是两两独立，一类是相互独立

相互独立一定能导出两两独立，但是两两独立并不能导出相互独立。

所以上面ABC相互独立而不是两两独立

结论

  • 注意点：两个事件独不独立，是看他是否满足$P(A\cap B) = P(A)\cdot P(B)$ 跟集合没有关系，所以别用韦恩图判断，是要搞脑子的。
  • 就比如说一个2位数，全集为{1，2}，P(E)=”第一个数字为1”，P(F)=”第二个数字为2”，那么$P(E\cap F) = \frac{1}{2}\cdot \frac{1}{2}=\frac{1}{4}$
  • $P(\overline F)$是第二个数字不为2，那么只能为1，$P(E\cap \overline F) = \frac{1}{2}\cdot \frac{1}{2}=\frac{1}{4}$
  • $P(\overline E)$是第一个数字不为1，那么只能为2，$P(\overline E\cap F) = \frac{1}{2}\cdot \frac{1}{2}=\frac{1}{4}$
  • $P(\overline E\cap \overline F) = \frac{1}{2}\cdot \frac{1}{2}=\frac{1}{4}$
  • 又如：

  • 又如：

  • 又如

解题逻辑：我们要先列出P(E)再列出P(F),最后与$P(E\cap F)$ 作比较

条件概率

  • The conditional probability of A given B. denoted by P(A|B),is compute as
  • $P(E|F)=\frac{P(E\cap F)}{P(F)}$

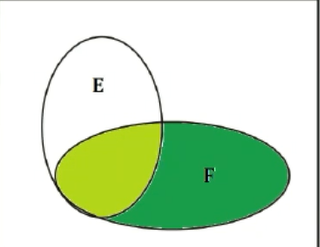
所以说是把样本空间改了一下，把原来的$\Omega$换成了我们的F

Question: What is the conditional probability that a family with two children has two boys, given they have at least one boy? Assume that each of the possibilities BB, BG, GB, and GG is equally likely.
Solution: Let E be the event that a family with two children has two boys, and let F be the event that a family with two children has at least one boy. It follows that E = {BB}, F = {BB; BG; GB}, and E $\cap$ F = {BB}.
Because the four possibilities are equally likely, it follows that P(F) = 3/4 and $P(E\cap F) = \frac 1 4$.
We conclude that
P(E|F) = P(E $\cap $ F)/P(F) = $\frac 1 3$

注意

  • 当A 和B都是独立的时候，P(E|F)=P(E)

答题格式，我们一定要分清楚 什么事件是E，什么事件是F，声明条件的是F，发生什么情况的是E。

然后我们求出$P(E\cap F)$

最后$P(E|F) = P(E\cap F)/P(F) $

What is the conditional probability that exactly four heads appear when a fair coin is flipped five times, given that the first flip came up heads/tails?

按照上面的步骤，我们知道F是第一次硬币为正面/反面，概率都是1/2

$P(E\cap F)$ 则是出现正面在5次中占据4次，那么如果第一次为正面，那么后面四次只要选3次即可，$P(E\cap F) = \frac{P(4,3)}{2^5} = \frac{1}{8} $
如果第一次为反面，那么后面四次必须全部为正面，那么$P(E\cap F)= \frac{1}{32}$

所以 $P(E|F) = P(E\cap F)/P(F) = \frac{1}{4}$ 或者 $\frac{1}{32}$

我们要特别注意:in a row, consecutive 这类的单词，因为这说明某些特定数字是连续的！

全概率公式（Total probability theorem)

  • $P(E\cap F) = P(E)\cdot P(F|E)= P(F)\cdot P(E|F)$
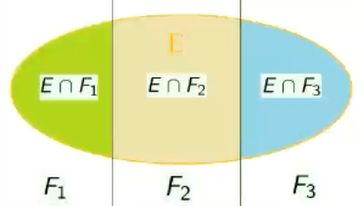
    • 通过上面这张图，我们可以得到全概率公式
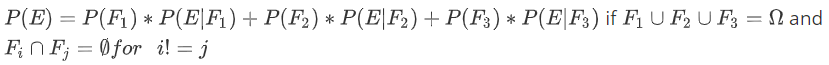
    • 可以以此类推.一直到n类，相当于一个分类讨论
  • 证明：

Bayes rule(贝叶斯公式)

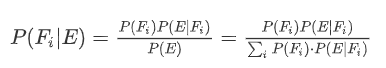
贝叶斯公式的应用

就是通过E来反推、预测 Fi的概率

我们假设Fi要么是男要么是女，E是这个人的属性，我们就可以计算$P(Female|Person)$或者$P(Male|Person)$

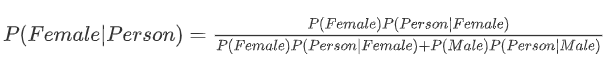
P(Person|Female)的意思就是如果这个人是女性，那么她长头发、高跟鞋的概率为多少。

所以这就是一个分类器，除了预测这是男是女，还可以预测你会不会买这个商品，一封邮件是不是垃圾邮件

这就是机器学习的方法之一，在数据科学领域是经常会用到的一个公式

例题

Question: Suppose we draw two cards from a well shuffed deck. What is the probability the second card in the deck is an ace?

Solution: Let E and F be events that the fi rst and the second cards are Aces, respectively. Hence $E$ and $\overline E$ is a partition of the sample space.

In terms of the total probability theorem, condition on whether the fi rst card is an ace or not:

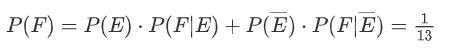
Question: 两根不同的标签，两个人抽签，公平吗？

Solution: 设第二次抽中长的概率为 P(F) = $\frac{1}{2}\cdot 0+\frac{1}{2}\cdot 1 = \frac{1}{2}$ 两个都是如此，所以是公平的，所以说，第二次抽中长的并不是一个条件概率

-------------本文结束，感谢您的阅读-------------