对坐标的曲面积分
有向曲面及曲面元素的投影
曲面分为双侧曲面(内外,左右,上下)和单侧曲面(莫比乌斯环)
- 指定了侧的曲面叫做有向曲面,其方法用法向量指向表示:

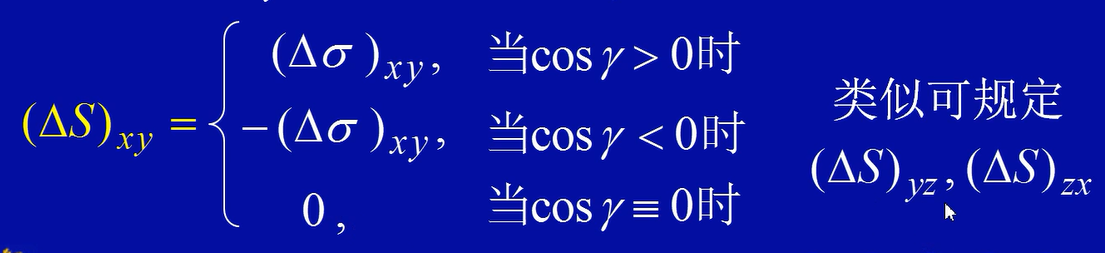
- 设$\Sigma$为有向曲面,其面元$\Delta S$在xOy面上的投影记为$(\Delta S){xy}$,$(\Delta S){xy}$的面积为$(\Delta\sigma)_{xy}>=0$则规定
对坐标的曲面积分的概念与性质
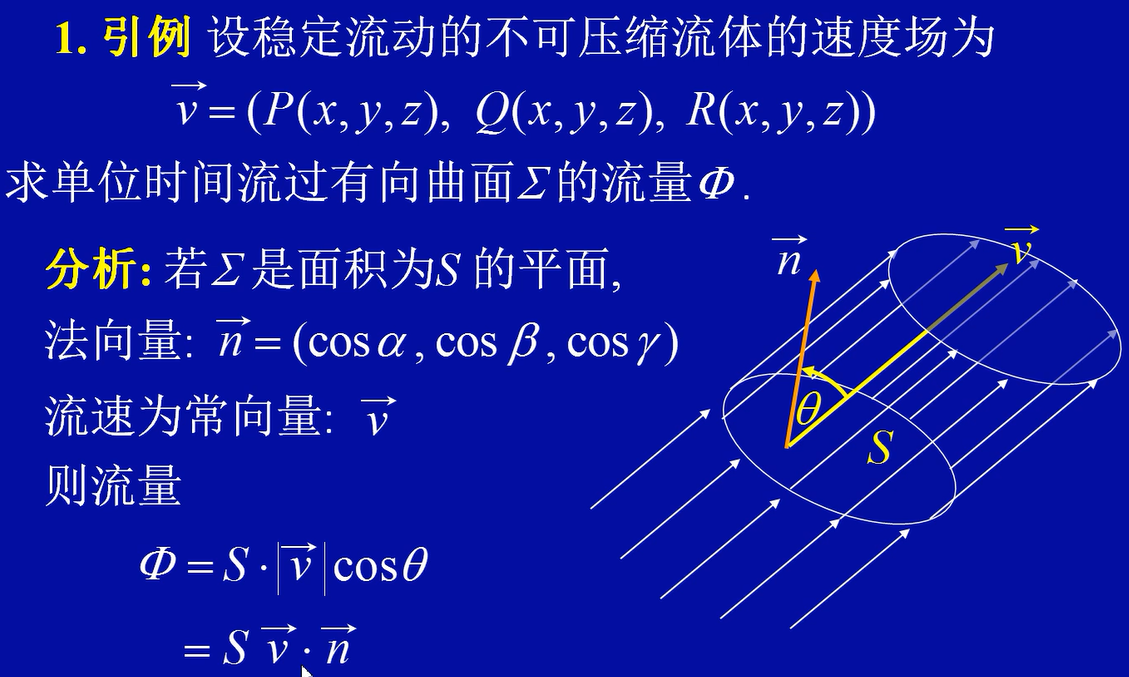

定义


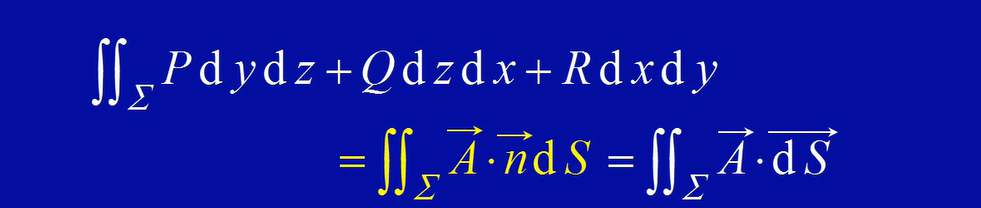
性质

对坐标曲面的曲面积分的计算法


例题
解题方法:
- 先看对称性,轮换性,把能变成0的都变成0
- 找到有效的面,判断取上侧还是取下侧
- 对dxdz,dydz,dxdy进行转换 利用$\frac{dz}{dx}=-\frac{F_x}{F_z}$等公式,最好划到xOy上
- 带入,求解二重积分。
例一

例二


第二类曲面积分刚好相反,如果曲面关于xOy对称,被积函数相对z来说,奇函数2倍,偶函数为0
例三

两类曲面积分的联系

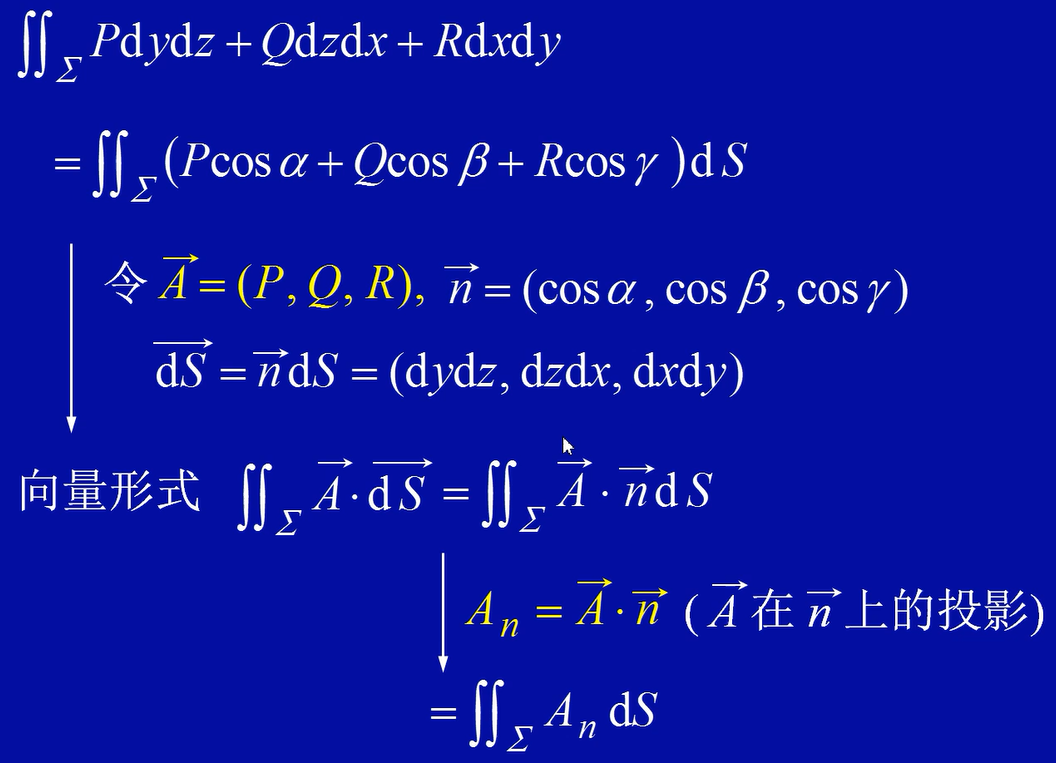
题形和注意点
题形:
求对坐标的曲面积分:
注意点
- 要注意有几个面,如果是一整个立体,千万不要忘记加顶面的积分,千万不要只计算侧面的积分
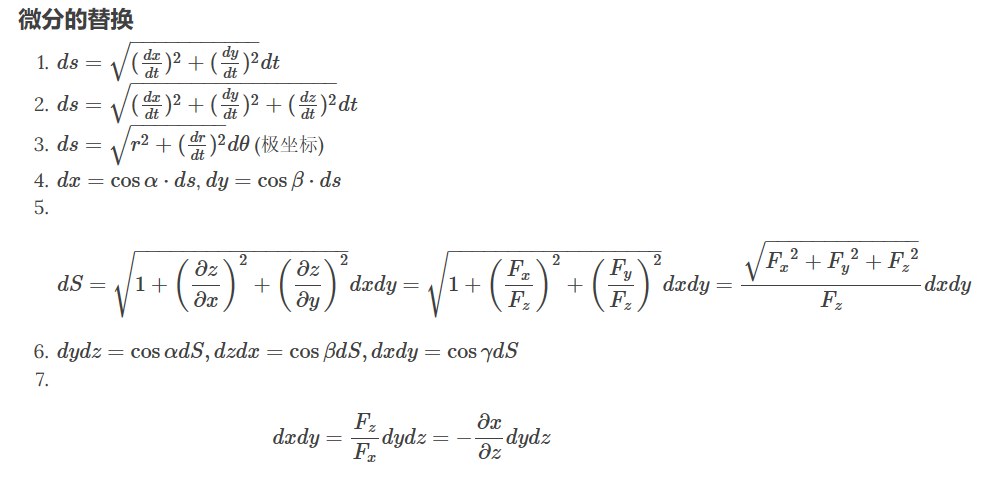
2.和其他积分相反,奇函数两倍,偶函数为0
书本练习


