二叉树
树的概念
树(Tree)是n(n≥0)个结点的有限集合,当n=0时,为空树;n>0时,为非空树。任意一棵非空树,满足:
1)有且仅有一个称之为根的结点;
2)除根结点以外的其余结点可分为m(m>0)个互不相交的有限集$T_1,T_2,…T_m$, 其中每一个集合本身又是一棵树,并且称为根的子树(SubTree)。


扇出:一个节点有多少个孩子
树的扇出:一棵树中扇出最大的节点
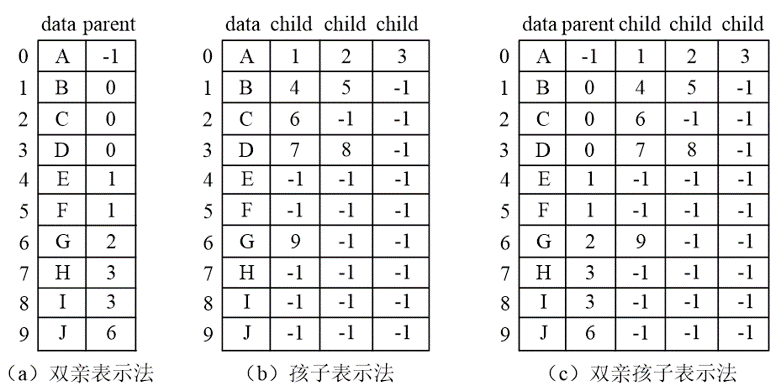
二叉树
二叉树(Binary Tree)是n(n≥0)个结点所构成的集合,它或为空树(n=0);或为非空树。对于非空树T满足:
1)有且仅有一个称为根的结点;
2) 除根结点以外,其余结点分为两个互不相交的子集T1和T2,分别称为T的左子树和右子树,且T1和T2本身都是二叉树。

性质6:如果二叉树空格节点全部画出,那么对于二叉树来说,空格节点的个数始终比数值节点多1
满二叉树: 如果一棵二叉树的 深度为 k, 结点数 $2^{ k+1 }-1$, 每层结点数都最大 ,则此二叉树称作满二叉树。
完全二叉树:如果一棵二叉树至多只有最下面的两层结点度数可以小于2,其余各层结点度数都必须为2,并且最下面一层的结点都集中在该层最左边的若干位置上,则此二叉树称为完全二叉树。即为,满二叉树去掉最下层最右边若干结点
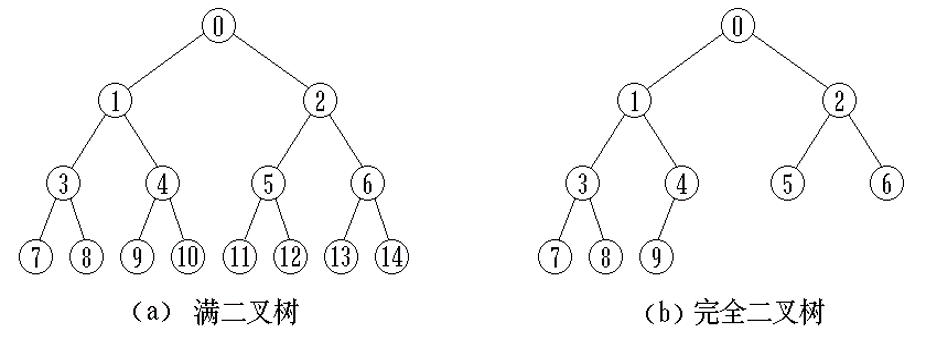
完全二叉树孩子与父亲的关系:
结点i的
左子结点是$2i+1$
右子结点是$2i+2$
父结点是 $( i-1)/2 $
二叉树的存储
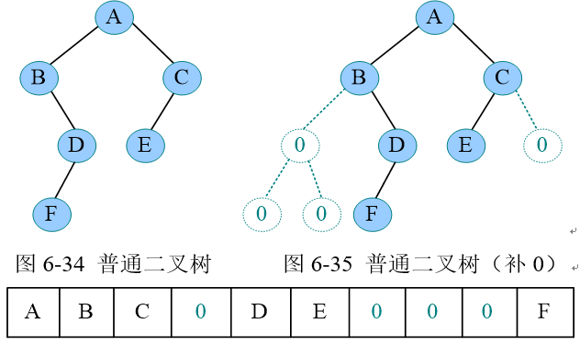
二叉树创建

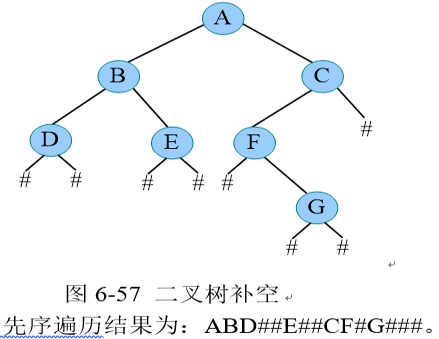
二叉树的遍历
按照根的访问顺序不同,根在前面的称为先序遍历(DLR),根在中间称之为中序遍历(LDR),根在最后面称为后序遍历(LRD)
先序遍历
先序遍历是指先访问根,然后先序遍历左子树,再先序遍历右子树
算法步骤:
如果二叉树为空,则空操作,否则
- 访问根节点
- 先序遍历左子树
- 先序遍历右子树
先序遍历秘籍:访问根,先序遍历左子树,左子树为空或已全部遍历才可先序遍历右子树
1 | void preorder(Btree T) |
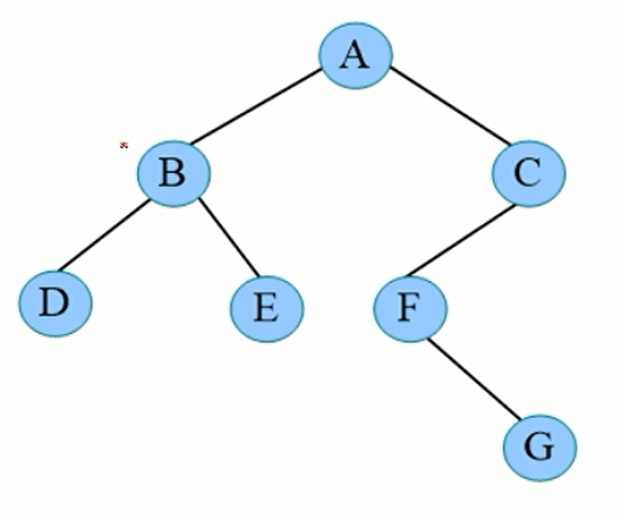
比如说这棵树,先序遍历就是A-B-D-E-C-F-G
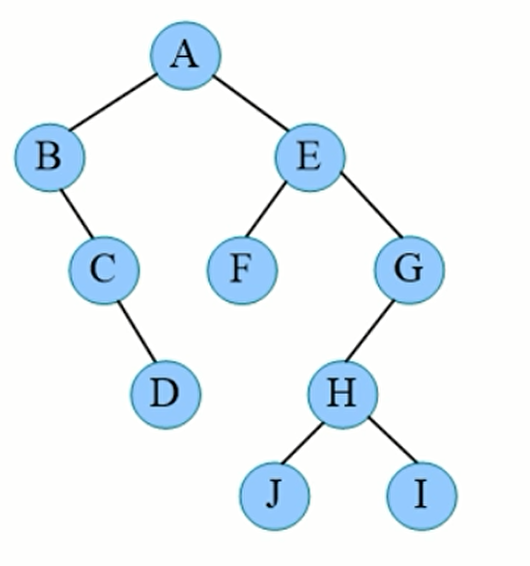
这棵树的先序遍历就是 A-B-C-D-E-F-G-H-J-I
中序遍历
中序遍历是指中序遍历左子树,然后访问根,再中序遍历右子树,即LDR
算法步骤:
如果二叉树为空,则空操作,否则
- 中序遍历左子树
- 访问根节点
- 中序遍历右子树
中序遍历秘籍:中序遍历左子树,左子树为空或已全部遍历才可以访问根和中序遍历右子树

比如这棵树的中序遍历就是 DEBAFGC

比如这棵树的中序遍历就是 BCDAFEJHIG
后序遍历
后序遍历是指后序遍历左子树,再后序遍历右子树,最后访问根,即LRD
算法步骤:
如果二叉树为空,则空操作,否则
- 后序遍历左子树
- 后序遍历右子树
- 访问根节点
后序遍历秘籍:后序遍历左子树,后序遍历右子树,左子树,右子树为空或已经便利了才可以访问根

比如这棵树的后序遍历就是 DEBGFCA

比如这棵树的后序遍历就是DCBFJIHGEA
1 | void pro_order(BiTree T)//后序递归遍历二叉树 |
二叉树的还原
我们要知道先序和后序是不可能创建或者还原一个二叉树的,所以我们要用先序序列、中序序列或者后序序列、中序序列画一棵二叉树
先序中序建立还原二叉树
算法步骤:
- 先序序列的第一个字符为根
- 再中顺序序列中以根为中心划分左右子树
- 还原左右子树
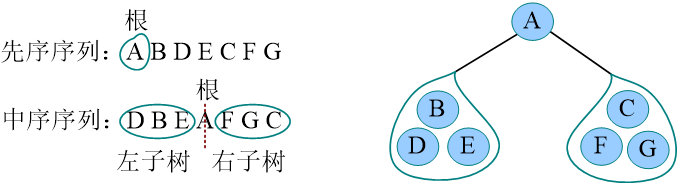
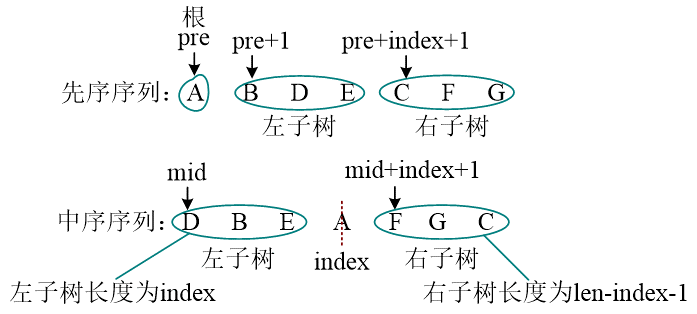
后序中序建立还原二叉树
算法步骤:
- 后序序列的最后一个字符为根
- 再中顺序序列中以根为中心划分左右子树
- 还原左右子树
1 |
|
层序遍历构建二叉树
1 |
|