高斯公式
高斯公式
定理1

例题1

思考:1若$\Sigma$ 改为内测,结果有何变化? -正负号
- 若$\Sigma$为圆柱侧面(外侧),如何计算? 先补上,符合高斯公式,然后再减去两个面
例题2


例题三

沿任意闭曲面的曲面积分为0 的条件

通量与散度





思考
- 曲面积分化为三重积分,不能用曲面去带!比如说直接化成体积,这是万万不可的
- 高斯公式要连续偏导数


题型与注意点
1.特别要注意原点。如果曲线(格林公式),曲面(高斯公式)包含原点,要关注曲线和曲面在原点是否有定义,比如说
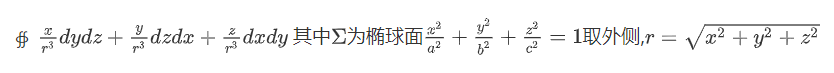
这题,因为包含原点,而且分母r^3^在原点是等于0的,所以我们要设计一个区域(一个在椭圆内部的小球),这里选择小球的原因是分母为r^3^ 如果是小球的话r就是一个常数了,所以直接可以提取出来再进行运算,这时候,对于小球,在原点就是导数了。
在格林公式的课本练习题中,也有这样一道题目

在这里,分母是$4x^2+y^2$ 这时候显然再取一个圆就不合适了,我们的目标就是把$4x^2+y^2$化成一个常数,所以我们就要取一个椭圆,$4x^2+y^2 = \varepsilon ^2$
2.和格林公式一样,但是比格林公式更坑的就是符号问题。请注意,封闭曲面只有内外侧之分

所以当运用高斯公式的时候,判断内外侧即可,不用判断夹角!!!!
书本练习


