python数据可视化之matplotlib
基本绘制图形
1 | matplotlib.use('TkAgg') |
注意,使用这行代码可以在鼠标移动的时候显示坐标信息
或者File -> Settings -> Tools -> Python Scientific -> 去掉Show plots in tool window勾选
绘制直线图
1 | import matplotlib.pyplot as plt |
效果如下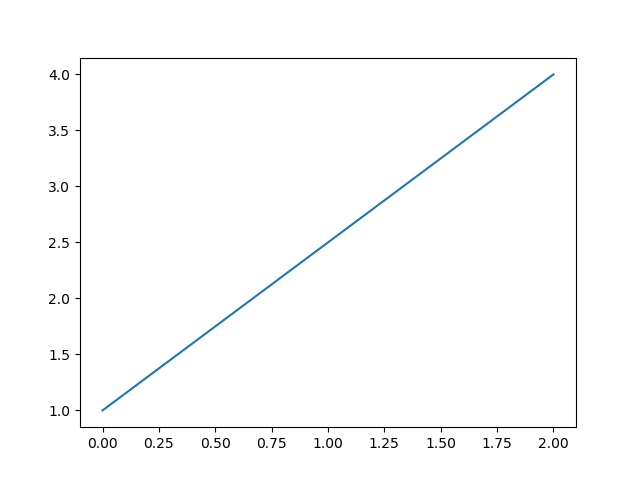
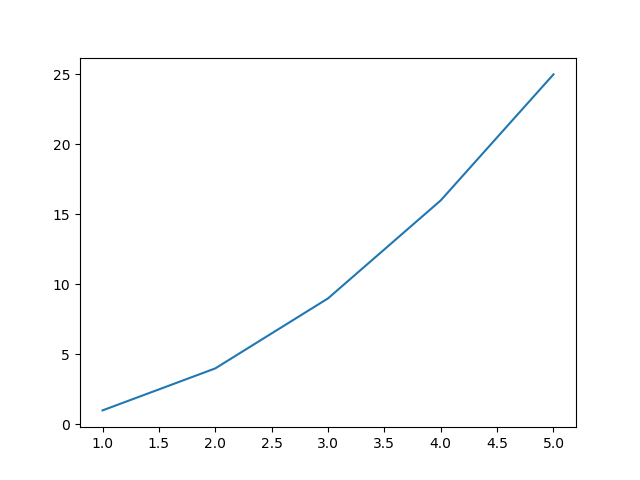
绘制折线图
1 | import matplotlib.pyplot as plt |
设置样式
设置标签文字和线条粗细
在上面的实例直线结果不够完美,我们可以对线条样式进行灵活设置。例如:可以设置线条的粗细,设置文字等等
1 | import matplotlib.pyplot as plt |
当标题为中文,那么会出现乱码,可以在上面加上一行代码
1 | plt.rcParams["font.sans-serif"]=["SimHei"] |
绘制曲线
一元二次方程
1 | import matplotlib.pyplot as plt |
绘制正弦余弦曲线
1 | import matplotlib.pyplot as plt |
subplot的使用
subplot()函数将画布分区
1 | import matplotlib.pyplot as plt |
通过 plt.xlim()和plt.ylim()修改坐标
1 | import matplotlib.pyplot as plt |
绘制散点图
利用散点图函数scatter 可以绘制随机点,该函数需要接收x坐标和y坐标的序列
1 | import matplotlib.pyplot as plt |
也可以通过
1 | plt.plot(x,sin_x,'o') |
这行代码来画出散点图。
从上面的示例可以看出,使用plot 绘制和使用scatter绘制出来的图形是没有区别的,但是使用plot绘制图形的速度优于scatter,所以如果画一堆点,而且点的形式没有差别,那么用plot即可,如果点的形式(大小,颜色)有差别,则必须使用scattter()函数
绘制大小颜色不同的散点图
1 | import matplotlib.pyplot as plt |
- 注意:
- 点的个数和颜色的个数一定要相同,多一点少一点都不行
- 点的个数和点的大小的个数可以不相同,如果点的个数大于大小的个数,则会循环获取大小
绘制不同样式和颜色的线条
格式化字符
| 字符 | 描述 |
|---|---|
| ‘-‘ | 实线样式 |
| ‘—‘ | 短横线样式 |
| ‘-.’ | 点划线样式 |
| ‘:’ | 虚线样式 |
| ‘.’ | 点标记 |
| ‘,’ | 像素标记 |
| ‘o’ | 圆标记 |
| ‘v’ | 倒三角标记 |
| ‘^’ | 正三角标记 |
| ‘1’ | 下箭头标记 |
| ‘2’ | 上箭头标记 |
| ‘3’ | 左箭头标记 |
| ‘4’ | 右箭头标记 |
| ‘s’ | 正方形标记 |
| ‘p’ | 五边形标记 |
| ‘*’ | 星形标记 |
| ‘h’ | 六边形标记 1 |
| ‘H’ | 六边形标记 2 |
| ‘+’ | 加号标记 |
| ‘x’ | X 标记 |
| ‘D’ | 菱形标记 |
| ‘d’ | 窄菱形标记 |
| ‘_’ | 水平线标记 |
以下是颜色的缩写:
| 字符 | 颜色 |
|---|---|
| ‘b’ | 蓝色 |
| ‘g’ | 绿色 |
| ‘r’ | 红色 |
| ‘c’ | 青色 |
| ‘m’ | 品红色 |
| ‘y’ | 黄色 |
| ‘k’ | 黑色 |
| ‘w’ | 白色 |
不同种类的不同颜色的线
1 | import matplotlib.pyplot as plt |
不同种类不同颜色的线并添加图例
1 | import matplotlib.pyplot as plt |
绘制柱状图
使用bar函数可以绘制柱状图。柱状图需要水平的x坐标值,以及每一个坐标值对应的y的坐标值,从而形成柱状的图。柱状图主要用来纵向对比和横向对比的,例如,根据年份对销售额进行纵向对比,x坐标值就表示年份,y坐标值表示销售数据
需要注意的是bar函数的宽度并不是像素宽度。bar函数会根据二维坐标系的尺寸,以及x坐标值的多少,自动确定每一个柱的宽度,而width指定的宽度就是这个标准柱宽度的倍数。该参数值可以是浮点数,如0.5,表示柱的宽度是标准宽度的0.5倍。
1 | import matplotlib.pyplot as plt |
barh函数的使用(水平柱状图)
1 | import matplotlib.pyplot as plt |
对柱体设置不同颜色
1 | import matplotlib.pyplot as plt |
柱状图示例
1 | import matplotlib.pyplot as plt |
绘制饼状图
pie函数可以绘制饼状图,饼图主要是用来呈现比例的。只要传入比例数据即可。
1 | #导入模块 |
绘制直方图
直方图与柱状图的分格类似,都是由若干个柱组成,但直方图和柱状图的含义却有很大的差异。直方图是用来观察分布状态的,而柱状图是用来看每一个X坐标对应的Y的值的。也就是说,直方图关注的是分布,并不关心具体的某个值,而柱状图关心的是具体的某个值。使用hist函数绘制直方图。
使用random函数生成1000个正态分布的随机数,使用hist函数绘制这1000个随机数的分布状态
1 | #导入模块 |
使用normal 函数生成1000 个正态分布的随机数,使用hist 函数绘制这100 个随机数的分布状态
使用np.random.normal()指定期望和均值的正态分布
1 | import numpy as np |
绘制等高线图和三维图
1 | #导入模块 |
使用pyplot绘制等高线图
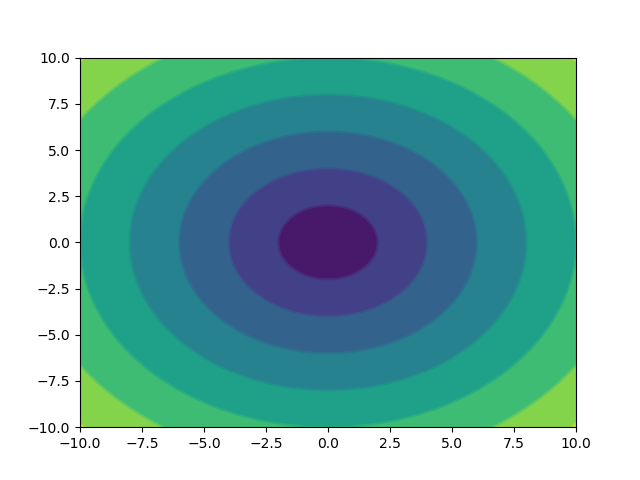
使用pyplot包和Matplotlib绘制三维图。
1 | import matplotlib.pyplot as plt |
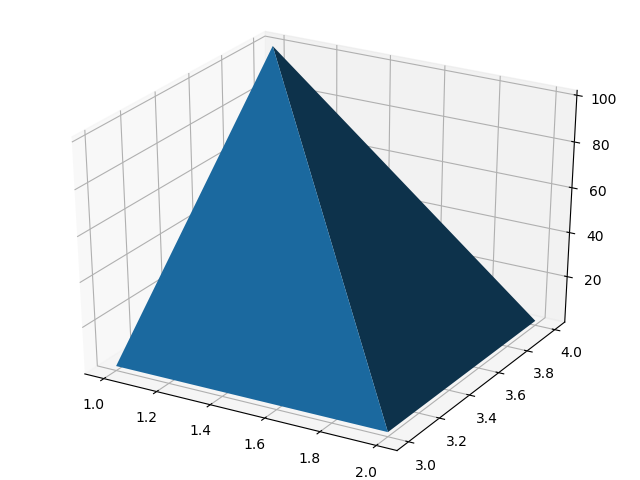
1 | import matplotlib |
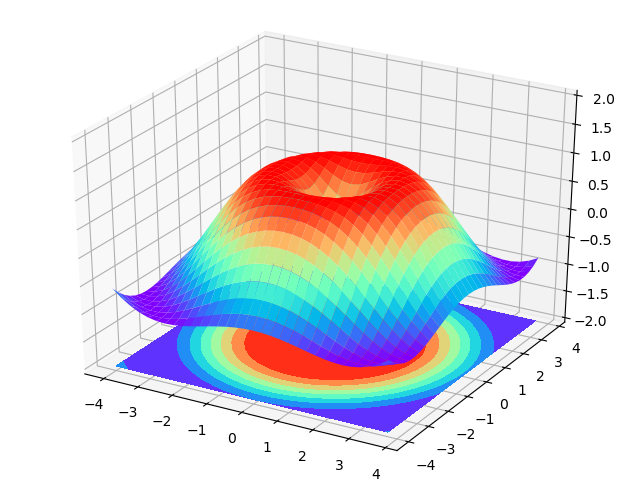
rstride = 5,cstride = 5的效果
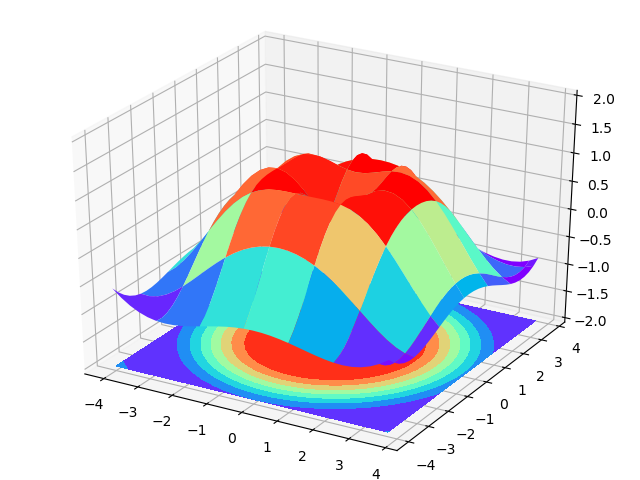
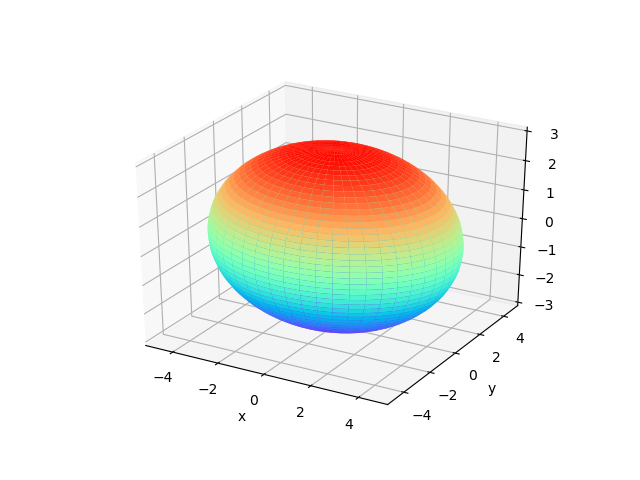
旋转抛物面
z = x^2^ +y^2^
1 | import numpy as np |
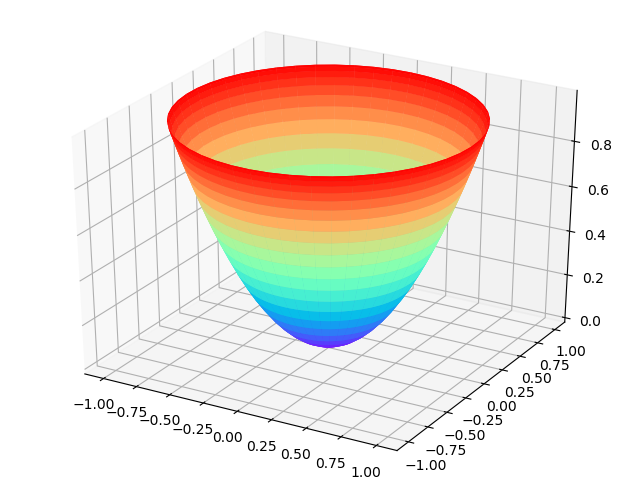
修改x,y,z可以得到y = x^2^ +z^2^
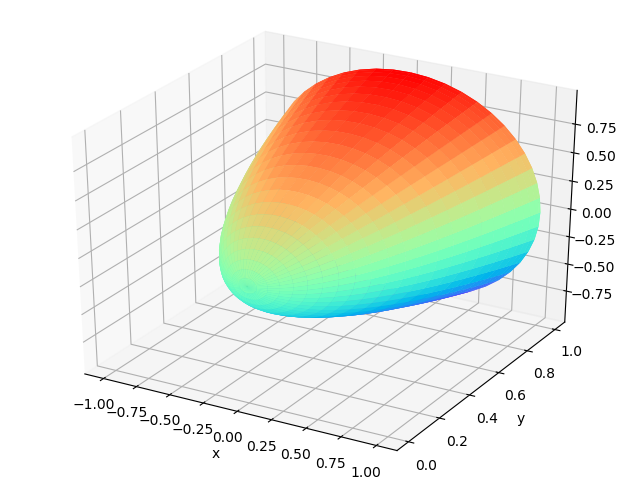
x =y^2^ +z^2^
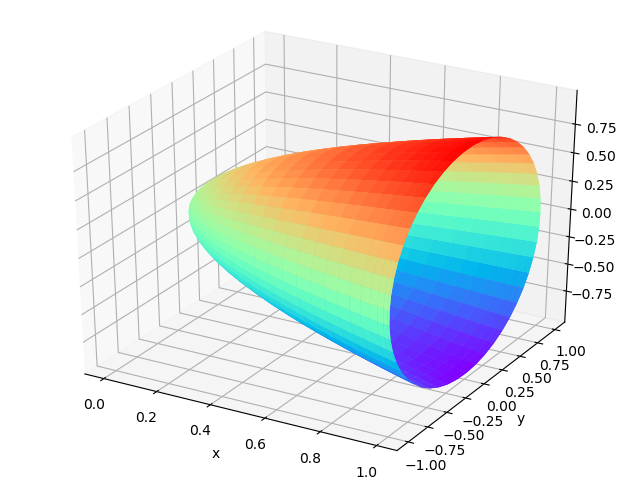
抛物面
圆柱面图
1 | import matplotlib |
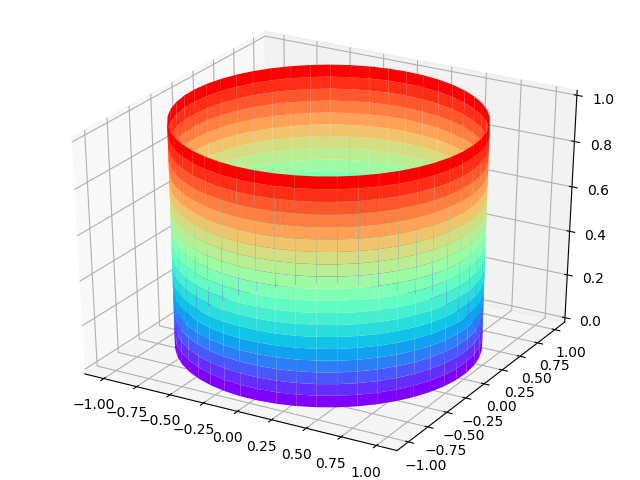
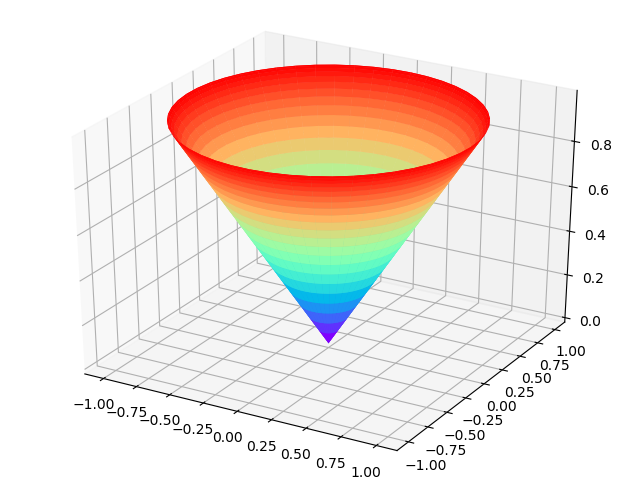
圆锥面
1 | import numpy as np |
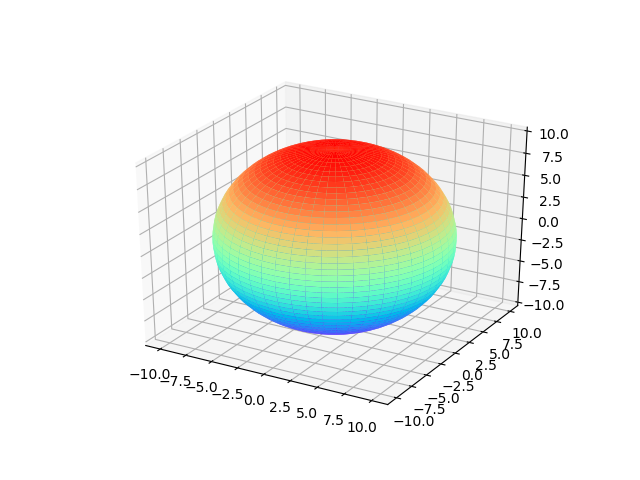
球面
1 | from mpl_toolkits.mplot3d import Axes3D |
椭球面
1 | from mpl_toolkits.mplot3d import Axes3D |