连通分量

Posted on | In
Words count in article: 2.6k | Reading time ≈ 11

连通分量

1.连通图和连通分量：

连通图：无向图中，如果顶点vi到vj有路径，则称vi和vj是联通的，如果图中任意两个顶点都是连通的，则称G为连通图。

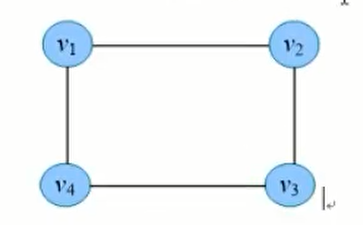
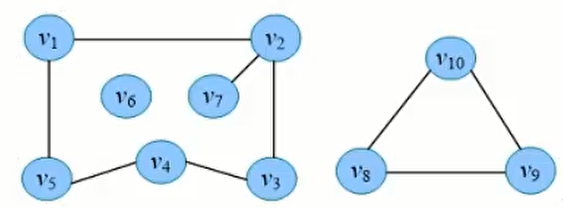
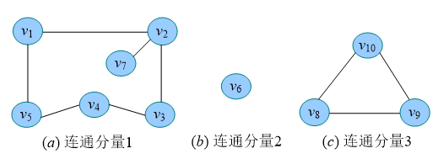
连通分量：无向图G的极大连通子图称为G的连通分量。极大连通子图的意思是：该子图是G的连通子图，如果再加入一个顶点，该子图不连通。下图中该图有三个连通分量。 对于连通图，则其连通分量就是他自己，对于非连通图，则有2个以上的连通分量。

2.强连通图和强连通分量

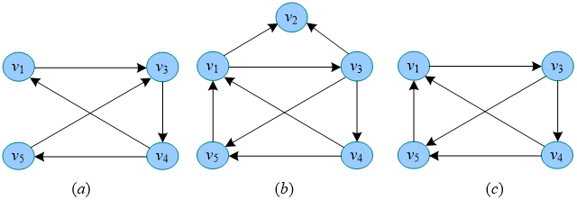
弱连通或者单向连通就是指只有一个方向相连.

3.无向图的桥与割点

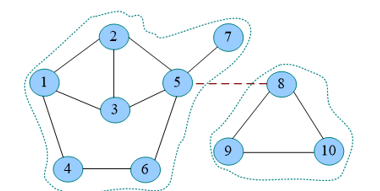
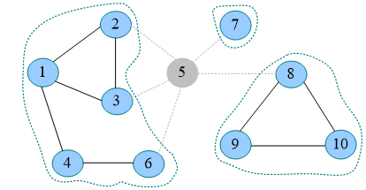
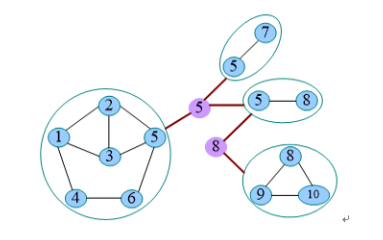
在生活中，桥就是连接河两岸的交通要道，桥断了，河两岸不在连通。在图论中，桥有着同样的含义。如图所示，去掉该边（5，8）后图分裂成两个互不连通的子图，边（5，8）就为图G的桥，同样，边（5，7）也是图G的桥

4. 无向图的双连通分量

  • 如果无向图中不存在桥，则称它为边双连通图，边连通图中，任意两个点间，存在两条或以上的路径，且路径上的边不重复

    • 比如说一个环路

  • 如果无向图中不存在割点，则称它为点双连通图，点连通图中，如果顶点数大于2，则任意两个点间，存在两条或以上的路径，且路径上的边不重复

    • 比如一个环路

  • 无向图的极大边双连通子图称为双连通分量，记为e-DCC

  • 无向图的极大点双连通子图称为点双连通分量，记为v-DCC

二者统称为双连通分量DCC

5. 双连通分量的缩点

e-DCC缩点

把每一个边双连通分量e-DCC看作是一个点，把桥看作连接两个缩点的无向边，得到一个树，这种方法称为e-DCC缩点，如图，生成了一棵树

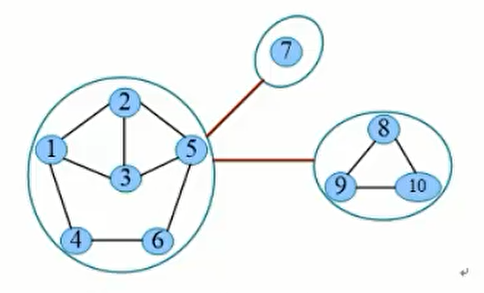
注意：边双连通分量就是删除桥之后留下的连通块，但点双连通分量并不是删除割点后留下的连通块

v-DCC缩点

把每一个点双连通分量v-DCC看作是一个点，把割点看成一个点，每个割点向包含他的v-DCC连接一条边，得到一个树， 如图， 这种方法称为v-DCC缩点。

如图所示，图G的点双连通分量有4 个（没有割点才能叫点双连通分量)

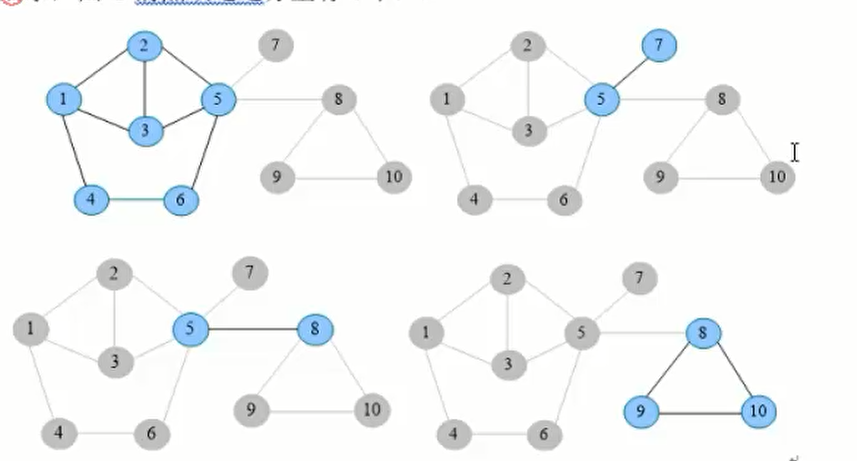
那么，我们得到的树就是：

Tarjan算法

  1. 无向图的桥．
  2. 无向图的割点
  3. 有向图的强连通分量

Tarjan 计算机科学家， 以LCA，强连通分量等算法闻名。Tarjan设计了求解应用领域的许多问题的广泛有效的算法和数拆结构。他以在数据结构和图论上的开创性工作而闻名， 他的 些著名的算法包括Tarjan最近公共祖先离线算法，Tarjan的强连通分量算法以及Link-Cut-Trees环法等。其中Hopcroft-!Tarjan平面嵌入算法是第一个线性时间平面算法。Tarjan 也开创了重要的数据结构，如斐波纳契堆和splay树， 另一项重大贡献是分析了并查集。 他是第一个证明了计算反阿克曼函数的乐观时间复杂度的科学家。

在介绍算法之前，首先引入时间戳和追溯点的概念

时间戳：dfn[u]表示u结点深度优先遍历的序号

追溯点：low[u] 表示u结点或u的子孙能通过非父子边追溯到的dfn最小的节点序号。即回到最早的过去

例如，在深度优先搜索中。每个点的时间戳和追溯点求解过程如下。

初始时，dfn[u] = low[u] ,如果该节点的邻接点未被访问，则一直使用深度优先遍历，1-2-3-5-6-4，此时4的邻接点1已经被访问，且1不是4的父节点，4的父节点是6（深度优先搜索树上的父节点）

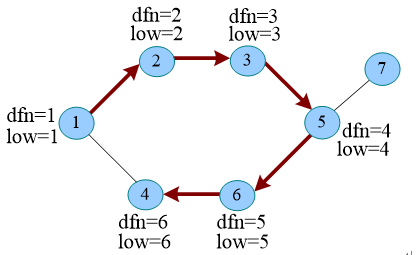
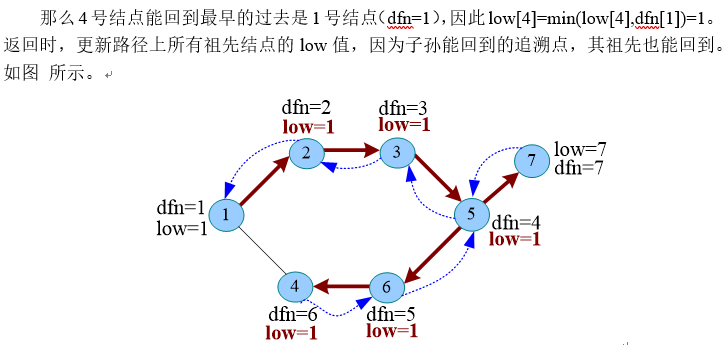
深度优先搜索书，起点就是根

无向图的桥

如何判断一条边是桥？

无向边(x,y) 是桥， 当且仅当搜索树上存在x的一个子节点y ，满足：

$low[y]>dfn[x]$

上图中边(5,7), 5的子节点7，满足$low[7]>dfn[5]$ ，因此这条边为桥。

算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include<iostream>
#include<cstring>
using namespace std;
const int maxn=1000+5;//节点数
int n,m;
int head[maxn],cnt;//头节点
//定义边
struct Edge
{
	int to,next;
}e[maxn<<1];
//定义low数组和dfn数组
int low[maxn],dfn[maxn],num;
//链式前向星
void add(int u,int v)
{
	e[++cnt].next=head[u];
	e[cnt].to=v;
	head[u]=cnt;	
}
void tarjan(int u,int fa)//u是出发点，fa是u的父节点
{
    //num一开始是0，先把结点的dfn和low都等于1
	dfn[u]=low[u]=++num;
    //访问u的所有邻接点（链式前向星）
	for(int i=head[u];i;i=e[i].next)
	{
        //v是u的第一个邻接点
		int v=e[i].to;
        //如果v是u的父亲(无向图中，父亲也是他的邻接点).那么什么也不做(不走回头路)
		if(v==fa)
			continue;
        //否则没有被访问的话，那么就从v开始深度优先遍历
		if(!dfn[v])
		{
			tarjan(v,u);
      //一定要更新u节点的low值，因为孩子的low值可以当作父亲的low值。取得最小的low值
			low[u]=min(low[u],low[v]);
       //当low[v]>dfn[u]那么就说 u-v是桥
			if(low[v]>dfn[u])
				cout<<u<<"—"<<v<<"是桥"<<endl; 
		}
		else
			low[u]=min(low[u],dfn[v]);
	}
}
//初始化头节点数组，low数组，dfn数组
void init()
{
	memset(head,0,sizeof(head));
	memset(low,0,sizeof(low));
	memset(dfn,0,sizeof(dfn));
	cnt=num=0;
}

int main()
{
	while(cin>>n>>m)//输入节点和边的数量
	{
		init();
		int u,v;
		while(m--)
		{
			cin>>u>>v;
			add(u,v);
			add(v,u);
		}
        //防止不连通节点的存在，查漏
		for(int i=1;i<=n;i++)
			if(!dfn[i])
				tarjan(1,0);//0是没有父亲的
	}
	return 0;
}

测试数据：

测试数据1 测试数据2
7 7 10 13
1 4 1 2
1 2 1 3
2 3 1 4
3 5 2 3
5 7 2 5
5 6 5 3
6 4 5 7
5 6
5-7是桥 5 8
6 4
8 9
8 10
9 10
5-8是桥 5-7是桥

割点判定法则

若x不是根节点，则x是割点，当且仅当搜索树上存在x的一个子节点y，满足：

$low[y]\geq dfn[x]$ (注意，刚才求桥的是大于符号，这里是大于等于符号)

若x是根节点，则x是割点，当且仅当搜索树上存在至少两个子节点，满足上述条件。因为我们想一下，如果只有一个子节点满足上述条件，那么就如下图的1，2结点，那么1就不是割点。

图中，5的子节点7，满足low[7]>dfn[5]因此5是割点

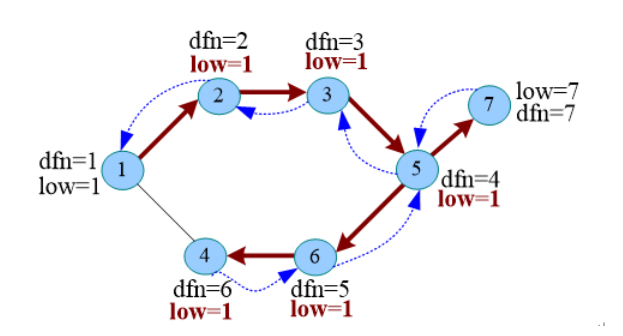
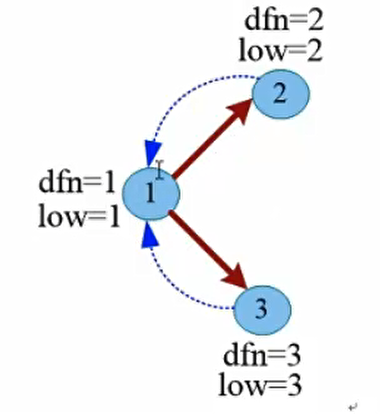
第二张图中，1是割点

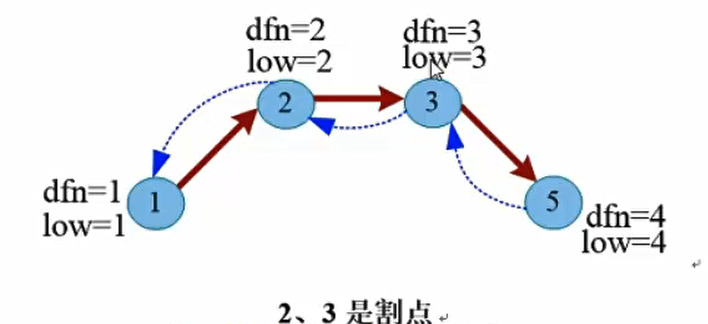
算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include<iostream>
#include<cstring>
using namespace std;
const int maxn=1000+5;
int n,m;
int head[maxn],cnt,root;
struct Edge
{
	int to,next;
}e[maxn<<1];

int low[maxn],dfn[maxn],num;
void add(int u,int v)
{
	e[++cnt].next=head[u];
	e[cnt].to=v;
	head[u]=cnt;	
}
void tarjan(int u,int fa)
{
	dfn[u]=low[u]=++num;
	int count=0;
	for(int i=head[u];i;i=e[i].next)
	{
		int v=e[i].to;
		if(v==fa)
			continue;
		if(!dfn[v])
		{
			tarjan(v,u);
			low[u]=min(low[u],low[v]);
			if(low[v]>=dfn[u])
			{
				count++;
				if(u!=root||count>1)
					cout<<u<<"是割点"<<endl; 
			}	
		}
		else
			low[u]=min(low[u],dfn[v]);
	}
}

void init()
{
	memset(head,0,sizeof(head));
	memset(low,0,sizeof(low));
	memset(dfn,0,sizeof(dfn));
	cnt=num=0;
}

int main()
{
	while(cin>>n>>m)
	{
		init();
		int u,v;
		while(m--)
		{
			cin>>u>>v;
			add(u,v);//无向图等于双向图
			add(v,u);
		}
		for(int i=1;i<=n;i++)
			if(!dfn[i])
			{
				root=i;
				tarjan(i,0);
			 } 
	}
	return 0;
}

有向图的强连通分量

算法步骤：

  1. 深度优先遍历结点，第一次访问结点x时，将x入栈，且dfn[x] = low[x] =++num
  2. 遍历x的所有邻接点y，
    • 若y没有被访问，则递归访问y，返回时更新low[x] = min(low[x],low[y])
    • 若y已经被访问且在栈当中，则令low[x] = min(low[x],dfn[y]);
  3. x回溯之前，判断如果low[x] = dfn[x] ，则从栈中不断弹出节点，一直到x出栈为止。弹出的结点就是一个强连通分量
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
#include<iostream>
#include<cstring>
#include<stack>
using namespace std;
const int maxn=1000+5;
int n,m;
int head[maxn],cnt;
stack<int>s;
bool ins[maxn];
struct Edge
{
	int to,next;
}e[maxn<<1];

int low[maxn],dfn[maxn],num;
void add(int u,int v)
{
	e[++cnt].next=head[u];
	e[cnt].to=v;
	head[u]=cnt;	
}
void tarjan(int u)
{
	low[u]=dfn[u]=++num;
    //标记元素是否在栈中
	ins[u]=true;
    //定义一个栈把u放到栈中
	s.push(u);
    //访问u的所有邻接点(发出边)
	for(int i=head[u];i;i=e[i].next)
	{
		int v=e[i].to;
		if(!dfn[v])
		{
            //如果没有被访问，继续深度优先遍历
			tarjan(v);
            //更新low[u]	
			low[u]=min(low[u],low[v]);
		}
        //如果已经访问过了，那么看看是否v结点在栈中
		else if(ins[v])
			low[u]=min(low[u],dfn[v]);//更新low值
        //因为u结点不止一个孩子，所以如果u的low值已经被很小的一个更新了，那么再次遇到dfn[v]
        //不一定比 当前的low[u]要小
	}
    //判断low[u]是否等于dfn[u]
	if(low[u]==dfn[u])
	{
		int v;
		cout<<"连通分量:";
		do
		{
			v=s.top();
			s.pop();
			cout<<v<<" ";
			ins[v]=false;
		}while(v!=u);//一直到把u出栈就停止
		cout<<endl;
	}
}

void init()
{
	memset(head,0,sizeof(head));
	memset(low,0,sizeof(low));
	memset(dfn,0,sizeof(dfn));
	memset(ins,0,sizeof(ins));
	cnt=num=0;
}

int main()
{
	while(cin>>n>>m)
	{
		init();
		int u,v;
		while(m--)
		{
			cin>>u>>v;
			add(u,v);
            add(v,u);
		}
		for(int i=1;i<=n;i++)
			if(!dfn[i])
				tarjan(i);
	}
	return 0;
}

gif来自：https://visualgo.net/zh/dfsbfs

连通分量: 0

连通分量: 1,2,3,4

连通分量: 5,6,7

-------------本文结束，感谢您的阅读-------------