无穷级数
常数项级数的概念
引例1.用圆内接正多边形面积逼近圆面积
依次作圆内接正$3 \cdot 2^n(n=1,2,\Lambda)$ 边形,设$a_0$表示内接正三角形的面积,$a_k$表示边数增加时增加的面积,则圆内接正$3\cdot 2^n$边形的面积为
$a_0+a_1+a_2+\Lambda+a_n$
当$n->\infty$时,这个和逼近圆的面积A,即$A=a_0+a_1+a_2+\Lambda+a_n$
引例2

引例3

定义
给定一个数列$u1,u_2,u_3..\Lambda,u_n,\Lambda$将各项依次相加。记为$\sum{n=1}^{\infty}u_n$
即$\sum_{n=1}^{\infty}u_n = u_1,u_2,u_3..\Lambda,u_n,\Lambda$
称上式为无穷级数,其中第n项 $un$叫做级数的一般项,级数的前n项和$S_n=\sum{k=1}^{n}u_k = u_1,u_2,u_3..\Lambda,u_n$ 称作级数的部分和
若$\lim\limits{n->\infty}S_n = S$存在,则称无穷级数收敛,并称S为级数的和记作$S=\sum{n=1}^{\infty}u_n$
若$\lim\limits_{n->\infty}S_n = S$不存在m,则称无穷级数发散
那么,当级数收敛时, $rn = S-S_n = u{n+1}+u{n+2}+\Lambda$ 为级数的余项,显然 $\lim\limits{n->\infty}r_n = 0$
例一:讨论等比级数(几何级数)
$\sum_{n=0}^{\infty}aq^n = a+aq+aq^2+\Lambda+aq^n+\Lambda(a\neq 0)$(q称为公比)的敛散性


例二:判断下列级数的敛散性



现在,我们只能通过前n项的和来进行判断

无穷级数的基本性质
性质1

级数各项乘以非零常数后其敛散性不变
性质2


性质3
在级数前面加上或去掉有限项,都不会影响级数的敛散性

性质4
收敛级数加括弧后所成的级数仍收敛于原级数的和

级数收敛的必要条件


例题

例题

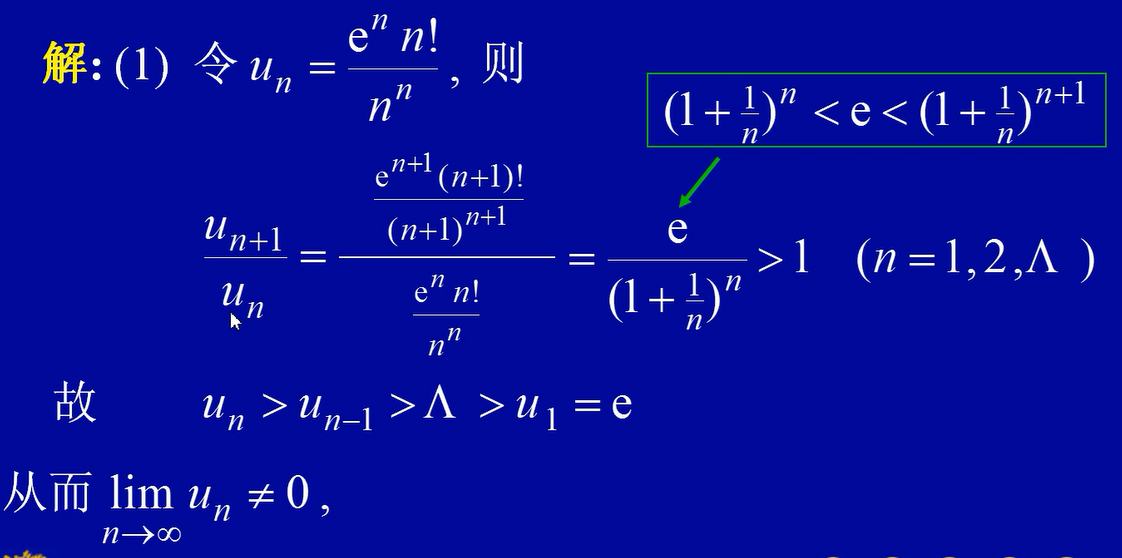


柯西审敛原理



解题方法
第一节的题目普遍比较简单。常常有这样的题形:
请用级数收敛发散的性质(定义) 判别下列级数的敛散性
那么我们可以用什么方法?
- 首先看看是否满足必要性。 必要性就是当n趋向无穷大的时候,单项是否趋于0,如果趋于零那么再做判断,否则直接写:“不满足级数收敛的必要条件,原级数发散”
- 这里还要注意,如果级数是周期波动的,比如 $\sin\frac{\pi}{n}$ ,是没有固定极限的,所以也发
- 其次看看是不是可以拆分成两个级数,然后通过级数的性质判断:
- 如果两个级数都是收敛的,其和其差一定是收敛的
- 如果两个级数有一个是收敛的有一个是发散的,那么其和其差一定是放散的
- 如果两个级数都是发散的,无法判断

