常数项级数的审敛法

正向级数及其审敛法

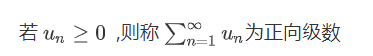
定理1

定理2（比较审敛法）

注意判断什么是强级数，什么是弱级数

定理3（比较审敛法的极限形式）

定理4 （D’alembert 判别法）

定理5（Cauchy判别法）

例题

例一：

例二：

例三：

例四：

例五：

例六：

例七：

例八

例九

解题注意

分母中有n，或者级数中有sinn，tann，log(1+n) (n趋向于0)这类可以等价无穷小替换

什么时候该用比较审敛法？

且与 调和级数，p级数相比为常数（当然存在0:0的话$v_n$收敛 $u_n$也收敛，或者无穷：无穷的话$v_n$发散，$u_n$发散)

什么时候该用比值审敛法？

当级数为分子分母形式，分子分母多为阶乘，幂函数。且 $\frac{u_{n+1}}{u_n}$ 是一个不为1 的常数，那么就可以用了

什么时候该用根值审敛法？

分子分母为$a^n$ 的形式，这样 $\sqrt[n] n$ 刚好就可以把这个n去掉

书本例题

交错级数及其审敛法

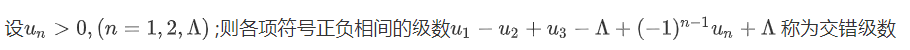
定理6

这里的$u_n$ 是没有符号的

例题

例一：

绝对收敛与条件收敛

例题

解题技巧

*绝对收敛级数的性质

小结

答题格式：

$\sum_{n=1}^{\infty}原级数$

$un\geq u{n+1} >0$ ? $\lim\limits{n->\infty}u_n=0$ ? => 根据 Leibniz 判别法，交错级数 $\sum{n=1}^{\infty}原级数$ 收敛

因为 $\sum{n=1}^{\infty}|原级数|=\sum{n=1}^{\infty}新级数$

根据比较、比值、根植判别法判别新级数是否收敛。如果收敛，那么原级数就是绝对收敛；如果发散，原级数就是条件收敛