Trie树
字典树又称Trie树,是单词查找树,是一种树形结构,也是哈希书的变种。典型应用于统计中,排序和保存大量字符串(但不仅仅限于字符串),所以经常被搜索引擎系统用于文本字频统计。它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无所谓的字符串比较,查询效率要比哈系树高
Trie树地3个基本性质:
- 根节点不包含字符,根节点外地每一个节点都只包含一个字符
- 从根节点到某一个节点,路径上经过的字符连接起来,为该点对应地字符串
- 每个节点的所有子节点包含的字符都不相同
所以每一个节点最多可以有26个子节点,对应26个字母(假设全部都为小写)。可以利用指针存储(比较浪费空间),也可以利用孩子兄弟表示法,也就是说可以利用左孩子右兄弟(比较难以理解)。一般指针表示最简单最直观。
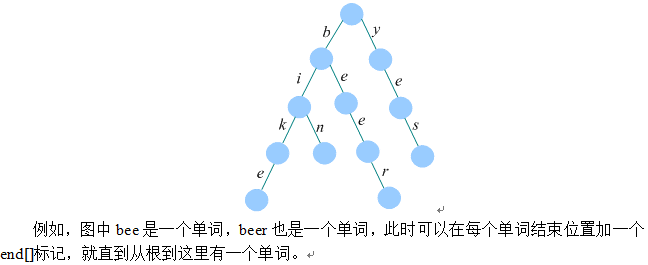
这里,我们如果只是想记录单词是否存在,那么end[]中可存放一个布尔值,如果我们想记录单词的个数,那么我们就需要存放一个数字,再次遇到的时候就++。所以我们要知道不一定是到了叶子,才是一个单词

字典树的创建


前一个[]中的数字是根的下标,后面一个是指针域。trie[1][1] = 2 的2是创建了第二个节点的意思,每个节点都是26个域。
然后判断第二个字符(i)s[1]-\’a\’ = 8 那么在 trie[2][8] 上判断是不是等于0,是等于0,我们把它改为3,表明创建了第三个节点
第三个字符(k)s[2]-‘a’ = 10 那么判断trie[3][10] 上判断是不是等于0,如果等于0,我们把它改成4,表明创建了第四个节点
第四个字符(e)s[3]-‘a’ = 4 那么判断trie[4][4] 上判断是不是等于0,如果等于0,我们把它改成5,表明创建了第五个节点
处理完毕后加上一个end[]标记,表示这是一个单词。
那么我如果再想要插入bin,那么发现trie[1][1] 不是0,那么说明b节点已经被创建过了,那么直接去找他就行了。
同样i也创建过了, n没创建过,那么就新建一个节点trie[3][13] = 4 ,同时加上end标记
算法代码
1 | void insert(string s) |
字典树的查找

代码实现
1 | bool search(string s) |
性能分析

树高最高是len,那么假设树都是满的,那么就有26^len^ 级别的
但这是最基础的解法,我们是可以优化的。
应用


- 我们可以利用哈希,对每一个单词统计,然后找最高的100个单词。还可以创建一棵字典树,然后找频率最高的100个词,利用end[]统计
- 过
- 过
- 可以利用end[]来标记,如果end=true 的话,什么也不用做即可。然后先序遍历即可; 如果要保留原来的顺序,那么可以碰到一单词,然后立即查询有没有,有的话立即删除;如果没有就保留
- 和第一题一样
- 去重+统计(把end[]改成 int型数组)


构建查找Trie树代码一览
1 |
|
例子:



字典树实现
1 |
|
Map实现
1 |
|