幂级数
函数项级数的概念


例子:

幂级数及其收敛性

Abel 定理
$a_n$ 没有限定!



因为在 $|x|<|x_0|$ 的时候,幂级数是绝对收敛的,所以说条件收敛的点只可能是端点!
定理二
$\Sigma{n=0}^\infty a_nx^n$ 的收敛半径为$R = \lim\limits{n\rightarrow \infty} |\frac{an}{a{n+1}}|$
例题:


非标准型

幂级数的运算

定理3


定理4


题型
收敛区间问题
首先拿到题目看看他是标准型还是非标准型
如果是标准型
那么计算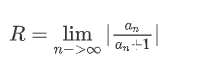 其中$a_n$是系数
其中$a_n$是系数
计算出了R的值以后,我们就得到了收敛半径。但是我们仍需要验证端点。
验证方法
把端点带入,因为左右端点导致的结果可能不相同,所以需要分类讨论
端点带入后得到一个常数项级数,然后利用定义(趋向无穷是否等于0)或者常数项级数审敛法来判断是否收敛。
如果收敛那么就取闭,否则取开。
如果是非标准型
那么就回到常数项级数审敛法,判断该用哪个审敛法:

用完以后我们会得到一个带着x的式子,一般是$x^2$ 然后我们需要求这个式子等于1 的解,为什么? 因为利用比值审敛法和根值审敛法得到的$\rho$ 都需要和1进行判断。
然后我们就解出x,这时候x就是端点。然后我们需要对端点带入进行判断验证
端点代入后得到一个常数项级数,然后利用定义(趋向无穷是否等于0)或者常数项级数审敛法来判断是否收敛。
变量代换
当形式不是$x^n$ 而是 $(ax+b)^n$ 形的时候,需要用一个变量代换。然后再按照上面的步骤解题
和函数问题


两个新的级数对应的收敛半径与原级数相同
解题步骤:
- 先求收敛半径->求得收敛区间
- 求和函数
- 求导
- 积分
- 列项
- 题除公因子
- 化为等比数列后求和/或者化成常见的泰勒展开后代换
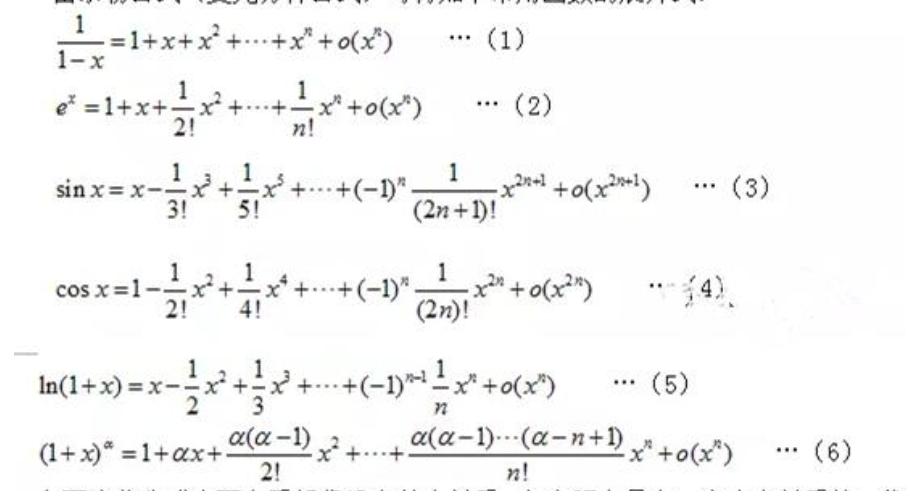
注意事项:
每个求和都写几项,要清楚是从n=几开始的!!!
分母或者系数中有 几的n次方之类的,可以和x^n 合并,然后极限改成 $\lim\limits_{x->\lambda x}…$ 在解出和函数后把x带换成 $\lambda x$ (比如例题5)
例一

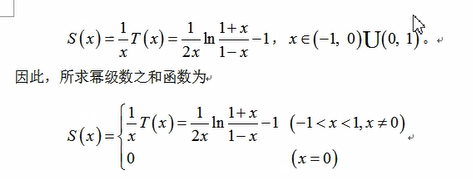
我们通过乘一个x或者除一个x,让幂次等于分母,这样就可以刚好消除。当然,提取出一个$\frac{1}{x}$ 之前首先要说明当x=0 的时候是什么情况,最后写成分类函数的形式
例二

没有分数,系数和幂次相差1(这里是n和n-1) 或者我们可以通过先提出一个数把格式化成能够积分的样子,然后用先积分再求导来做
例三
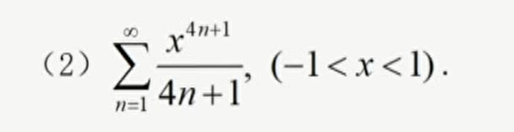
分母有n,同样用求导来做

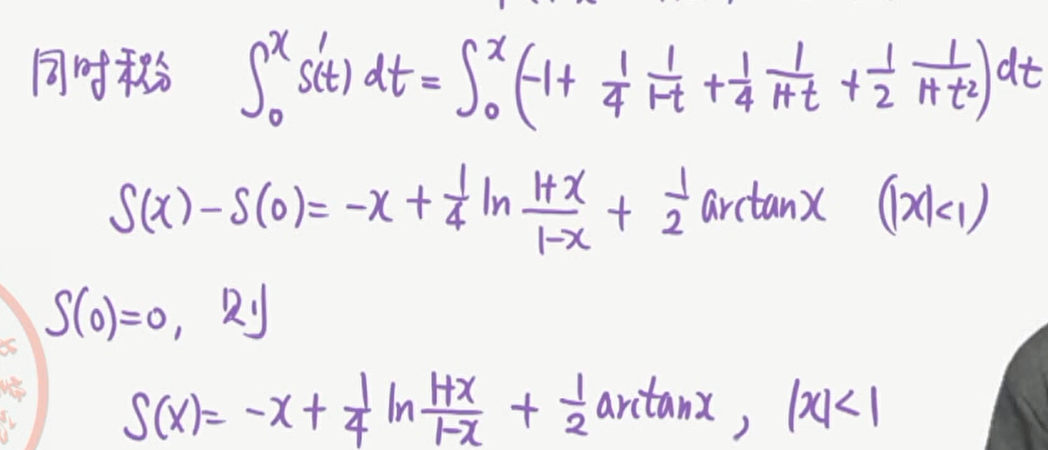
例四


例五
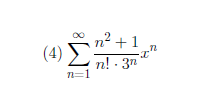
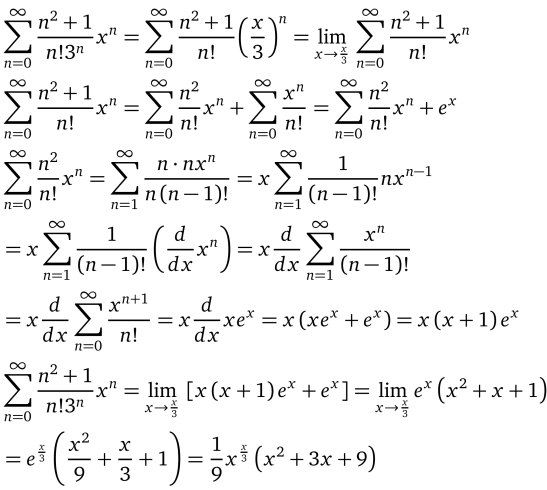
练习册选题:
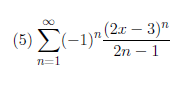

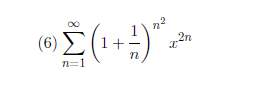

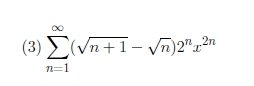

书本练习


