离散数学之关系1

Relation
Binary Relation

这样所有的二元运算符都可以成为一种关系,或者父子师生也可以成为一个关系

这个和我们的函数有点像,但是显然不是函数(一个x可以有多个指向),所以我们可以把关系看成一个函数的推广。函数本身就是个关系
Function as relations

Relations on a set

- 可以在一个集合中定义关系,比如说a能被b整除;或者a<=b,a>b等等
Representing Relations
Matrix representing
也就是说如果$(a_i,b_j) $满足关系,那么这点上的数据就是1,否则就是0

Digraph definition
利用有向图来存储。如果a指向b,那么关系就是a在前,b在后
那么如果a到a有一条边,那么这就是一个自环

Question: How many relations are there on a set with n elements?
Solution:
A relation on a set A is a subset of A X A. Because A X A has n^2^
elements when A has n elements. A set with m elements has 2^m^ subsets, there are $2^{m^2}$ subsets of AXA.
Thus, there are $2^{n^2}$ relations on a set with n elements.
For example, there are $2^{3^2} = 2^9 = 512$ relations on the set {a,b,c}
也就是说一个集合中的关系是非常非常复杂的
Properties of Relations
Reflexive 自反

那么R1不是自反的,因为里面没有(3,3)
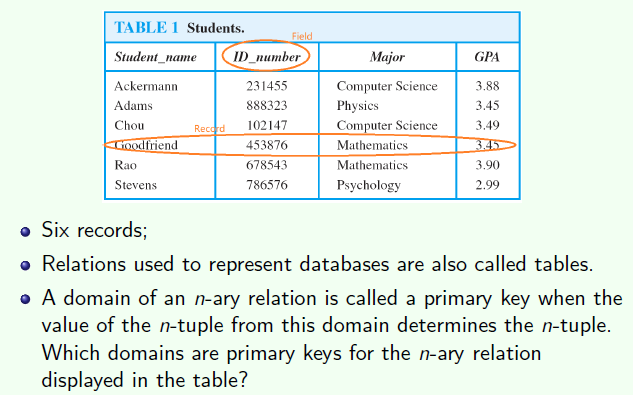
自反关系在图里面表示为一个自环,如果在矩阵上则是 对角线上都为1
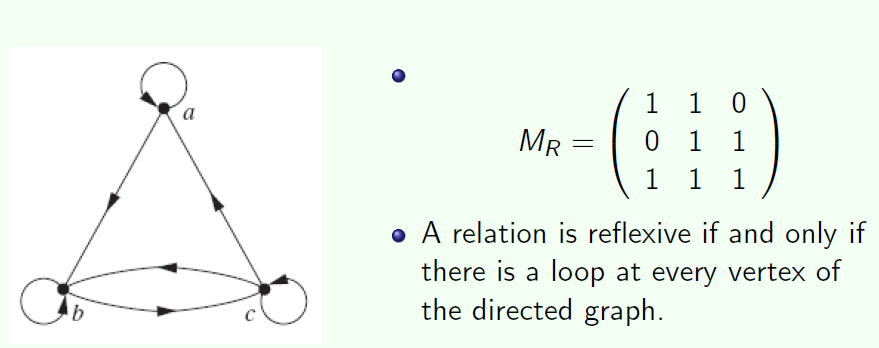
Symmetric and antisymmetric 对称和反对称
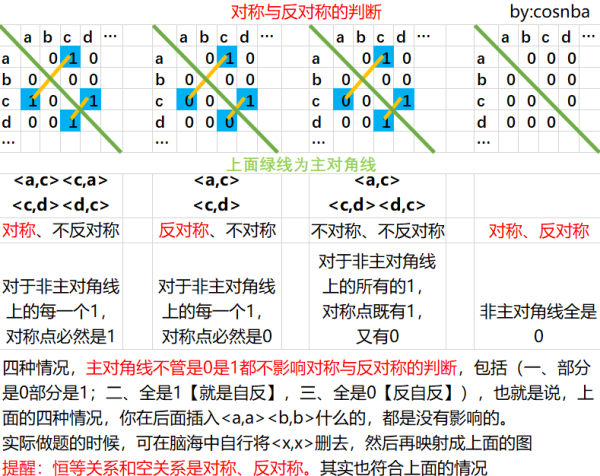
A relation R on a set A is called symmetric if $(b,a) \in R$ whenever $(a,b) \in R$, for all $ a,b \in A$.
对称的就是如果$(b,a) \in R$,那么必然 $(a,b) \in R$, 在矩阵中表示,就是非主对角线上的每一个1,对称点必然是1.
比如说我们的同学关系,相似关系,成比例关系,都是长头发,同一天生日,来自同一个地方,都是对称的。
A relation R on a set A such that for all $ a,b \in A$. if $(a,b) \in R$, and $(b,a) \in R$, then a = b is called
antisymmetric.
反对称关系,也就是说对于非主对角线上的每一个1,对称点必然是0。 比如大于等于(a>=b,b>=a ,那么a=b), a和b的整除(a能整除b,b能整除a,那么a=b)关系。

Transive 传递性


我们看到只有R3是具有传递性的
R1:(3,4),(4,1) 但是没有(3,1)
R2:(4,1),(1,2) 但是没有(4,2)
传递性在图中的表现:、
A relation is transitive if and only if whenever there is an edge from a vertex x to a vertex y and an edge from a vertex y to a vertex z, there is an edge from x to z (completing a triangle where each side is a directed edge with the correct direction).
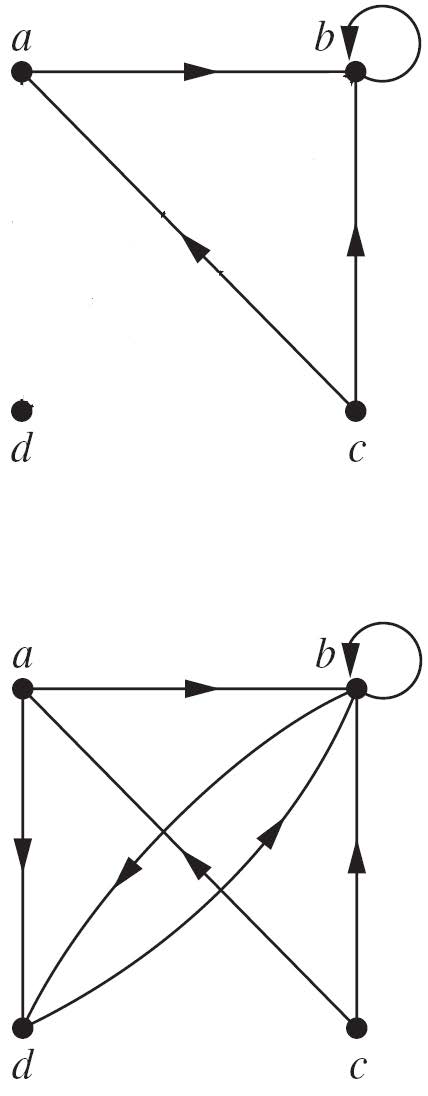
也就是说在图中具有传递性的话,三个点之间必然有一个三角形,且一条边的向量等于另外两条边的矢量和。
如下图。上面的那张是有传递性的,下面那张没有传递性。因为缺少了c->d,因为已经有c->a和a->d了,所以一定要满足三角形才具有传递性
Irreflexive 非自反性
Irreflexive代表了对角线上不能出现 1
Asymmetric 非对称
当$(a,b)\in R$时,$(b,a)\notin R$ ,也就是说对角线上必须全部为零且满足反对称
n-ary relations
n元关系:现在我有n个集合,现在n元关系就是这n个集合的笛卡尔集的子集。n称为它的度
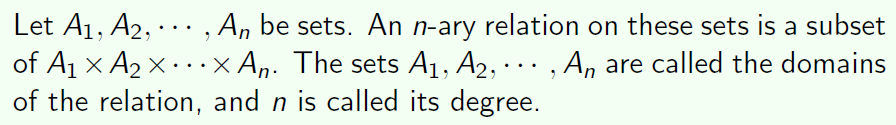
比如说第一个3元关系,关系是a<b<c,那么很明显(1,2,3) 属于R,(2,4,3)就不如与R了
第二个三元关系:定义在整数集上面,(a,b,c)为等差数列
第三个三元关系:a与b是同模的,也就是a与b除以m余数相等
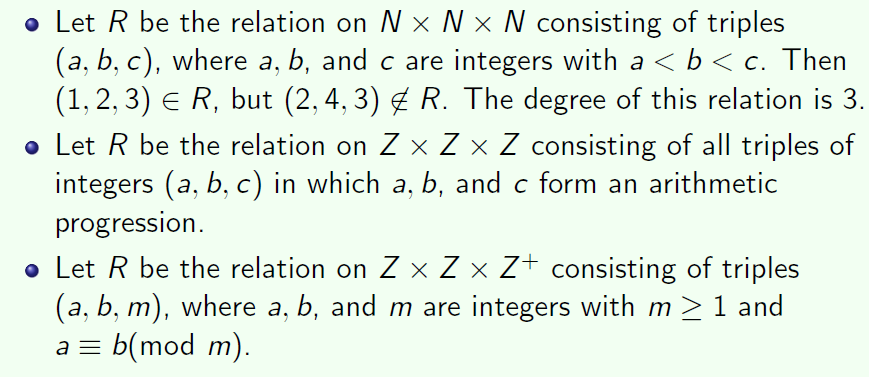
n元关系的应用就是数据库,数据库中每一个字段都可以成为一个集合,这张表就是这四个集合组成的笛卡尔集中的一部分,也就是一个n元关系。
Relation Operators
Operations on Binary Relations
交、并、差、亦或

复和 Composite
也就是说R是A与B之间的关系,S是B和C之间的关系。那么R和S的复合定义如下

也就是说设 R 为 X 到 Y 的关系,S为 Y 到 Z 的关系,则$R\circ S$称为R和S的复合关系 $S\circ R = {
至少存在一个b,也可以存在多个b
答题格式:
- $R_1\circ R_2{(a,c)\in R^2|\exists b \in R: (a,b) \in R_1 and (b,c) \in R_2 }$
- 将 $(a,b)$ 代入$R_1$, $(a,c)$带入$R_2$
- 得到$(a,c)$ 满足的关系式
- 因为结果是a和c的关系是,相对于b独立,我们可以将c重命名为b,转换成a和b的关系式

这一题能帮我们更好地理解这些运算。
a: $R_1\cup R_2$ 就是 a divides b or a is a multiple of a $\Rightarrow$ a divides b or b divides a
b: $R_1\cap R_2$ 就是 a divides b and a is a multiple of a $\Rightarrow$ $a=\pm b$ 又因为a需要当分母,所以 $a\neq 0$
c: $R_1 - R_2$ 就是 a divides b but a is not a multiple of b $\Rightarrow $ a divides b and $a\neq \pm b$
d: $R_2-R_1$ 就是 b divides a but b is not a multiple of a $\Rightarrow $b divides a and $a\neq \pm b$
e: $R_1\oplus R_2$ 为异或: a divides b or a is a multiple of a but not both $\Rightarrow$ (a divides b or b divides a) and $a\neq \pm b$
Power 幂运算
$R^{n+1}$相当于 $R^n$ 和R的附和
$R^1 $ 就是走一步能不能到,$R^2$ 就是走两步能不能到,$R^3$ 就是走三步能不能到(4->3->2->1)(2->1->1->1),以此类推

Property of transitive

用矩阵表示传递
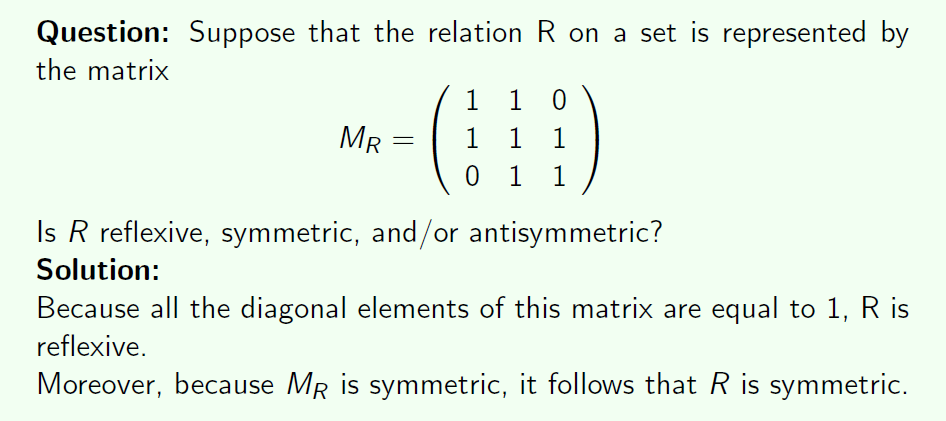
矩阵运算
矩阵的点乘,就是先做合取,再做析取

Example:
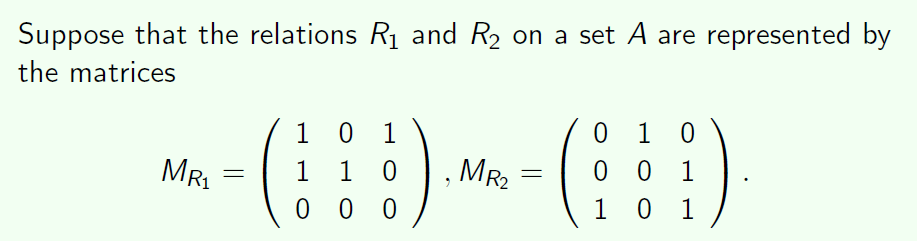

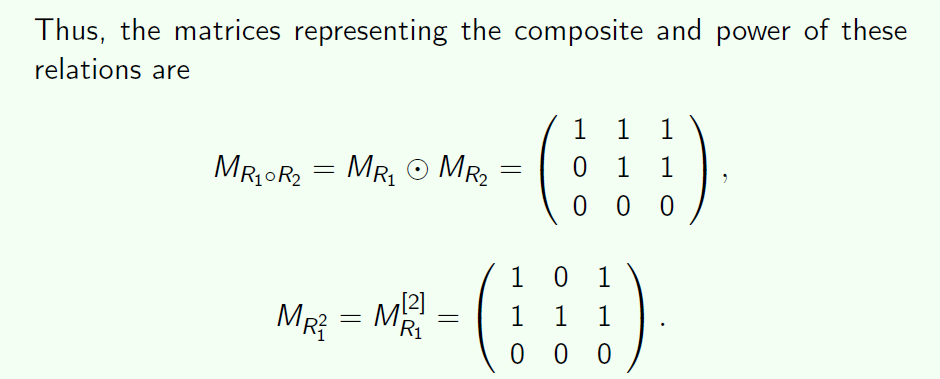
Operations on n-ary Relations
select

Projection
只看两个维度

Join
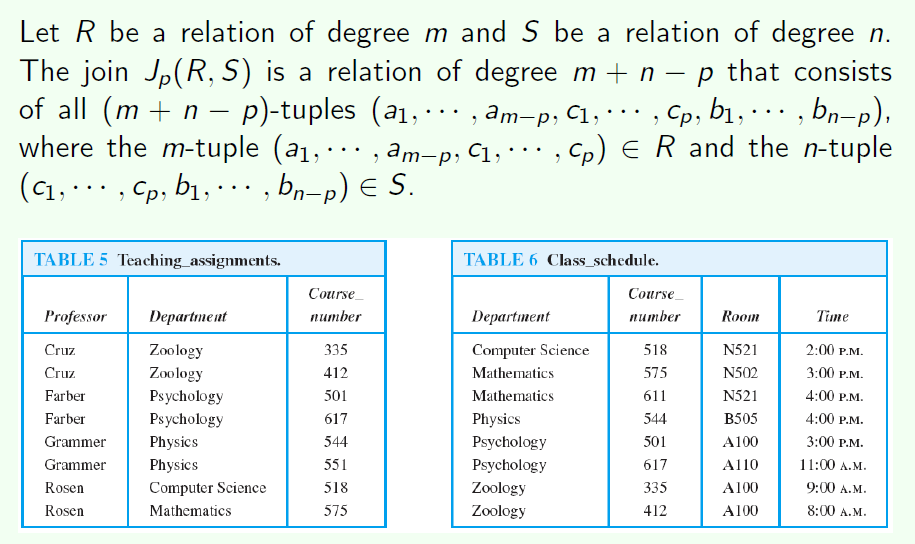
Join完了之后得到了一张新的表格