离散数学之关系2

Closures of Relations 闭包

设R是非空集合A上的关系,在关系R中,可能有或无性质P,如自反(r),对称(s),传递(t),若存在包含R,满足性质P的关系S,使得S是所有包含R,满足P的关系的子集,那么称S是R关于P的闭包(有时这样的闭包不存在)
所以我原来R可能不是闭包,但是我可以往里面加点东西,让它变成一个闭包。加进去的东西和原来的R就构成了我们的S
自反闭包
如果我们要满足自反性,那么(a,a) 一定要属于R,所以我们把小于改成小于等于即可
自反闭包在图中表现为自环。让我们补全要素称为自反闭包可以是集合形式也可以是图的形式。

如果R是自反性的,那么 $R^{*}$ 也是自反的。因为\
$R\subseteq R^,(a,a)\in R\Rightarrow (a,a)\in R^$
但是请注意,如果R是irreflexive的,也就是$(a,a)\notin R$ 但是 $R^2$ 却不一定是irreflexive的,比如说R对角线上全是0,然后其余部分都是1,也就是说如果$(a,b)\in R, (b,a)\in R$ 那么$(a,a)\in R\circ R = R^2,(b,b)\in R\circ R = R^2$
对称闭包

那么在图上又如何展示对称闭包呢?因为(a,b)在关系内,(b,a)也一定要在关系内,所以在图中表现为只要两点直接又连线,那么这个连线一定要有两根,a指向b,b指向a
如果R是对称的,那么$R^*$ 也是对称的:
假设让$(a,b)\in R^$, 那么a和b之间存在一组有序对$(s0,s_1)\in R,(s_1,s_2)\in R,\cdots(s{j-1},sj)\in R$ ,起点是a,终点是b。那么因为$R$ 是对称的,所以必然有$(s_j,s{j-1})\in R,(s{j-1},s{j-2})\in R,\cdots(s_2,s_1)\in R$
这就说明,从b到a也有一条path存在,于是 $(b,a)\in R^$ ,得证。
传递闭包

图G可以看作是一个关系,path可以看作是一条路径。$X_0$ 是起点, $X_n$ 是终点,一共走了n条边
$X0,X_1…X{n-1}$ 可以是一样的,是可能等于a的,也可能等于b,如果k出现了两次那么意味着先走到$X_k$绕了一圈又回到了$X_k$ 那么就说明这个路径中有一个环。如果a和b是同一个顶点,那么就是a出发绕了一圈回到了a,这就是个环。
path的长度为n,说明走了n步一定是可以到达目的地的,所以对应的位置上一定是1
定理1:
这就是说R的基础上构造了一个新的关系$R^n$。 R是集合A当中的一个关系。那么如果 有一条a到b之间长度为n的路径的话,那么 (a,b)就属于$R^n$
可以用数学归纳法证明:
如果path长度为1,那么$(a,b)\in R$ 成立,假设当 n=k的时候成立,那么当n=k+1的时候,找一点c,把原来的路线拆成两段,$(a,c)\in R,(c,b)\in R^n$ 那么根据复合法则,$(a,b)\in R^{n+1}$
如果$(a,b)\in R^n$那么至少存在一个长度为n的path,从a点(起点)走到b点(终点)

connectivity relation 连接关系

这个$R^$ 的意思是说这条路径可长可短(至少为1),无法确定。R\ 包含的是a到b的可达,只要a走到b就可以了,走多长的路我不管。$R^*$ 是很难算的,因为这是1到无穷
下面这个例子:$R^n$ 的意思就是 a通过n-1 个人可以认识b,$R^*$ 则是a可以认识b,但是不知道要通过多少人
定理2:
$R$的传递闭包,就是$R^*$
原来的R可能不满足传递性,但是我们可以通过往里面加点什么让他满足,这是闭包的定义
那么包含R,且满足传递性的最小的那个关系就叫做传递闭包。所谓最小的,就是任意拿一个包含R的传递关系过来都是R*的超集。
证明:
首先要证明R*具有传递性
其次要证明R*属于S

证明 S 是具有传递关系的,那么 $S^n$ 也是具有传递关系的
现在我假设 $(x,y)\in S^n,(y,z)\in S^n$ 我希望得到$(x,z)\in S^n$ 这个结论
因为$S^n \in S$ 所以 当n=1,2,3…的时候都满足。
现在 已经知道 x到y有n步,也就是说有n-1个内部节点。我们可以画出类似简图

同样,从y到z也可以画出一个相应的草图,所以(x,z)可以先从x走n-1步走到y,然后再从y一步走到z,这样$(x,z)\in S^n=S^{n-1} o S$ 就满足了
计算方法1
引理1
A中有n个元素,那么如果有一条path从a走向b,那么这条path不会超过n
更进一步来说,如果a!=b的话,那么这条path长度不会超过n-1

定理3
从引理可以知道我们没有必要把$R1,R_2,R{\infty}$ 都并起来,我们只需要并到n即可求出传递闭包。因为最多往前走n步嘛

例子:
如果我们要找3个顶点的传递闭包,我们只要算3个矩阵相并即可

算法

这个复杂度很高,有$O(n^4)$
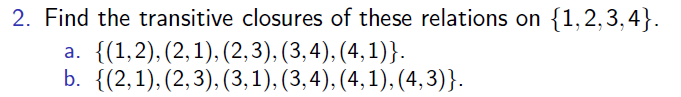




计算方法2
内部顶点:
位于起点和终点之间的节点都是内部节点

我们定义一个01矩阵W,令$W0= M_R$ ,那么 我们可以给出如上$W{ij}^k$ 的定义
$W^1$也就是说如果$Xi,X_j$ 可以通过$v_1$连起来的,$W{ij}$取1,或者$X_i,X_j$直接可以到达的,那也可以取1,否则取0.所以$W^1$只保留了$X_i$通过$v_1$到达$X_j$ 的 $v_1$相当于 它们之间的桥梁。 $W_2$就是以此类推,通过$v_1,v2$ ,$X_i$可以到达$X_j$
那么$Wn$ 的话,我们 的中间节点就有$V_1,V_2…V_n$ ,所以说$W^n{ij}$当中当且仅当$X_i$到$X_j$存在path(内部顶点可以取$V_1,V_2…V_n$)的时候,取1,否则取0。
那么我们就可以说 $W^n$ 就是 R 的传递闭包。
例子:


引理
要么本来$V_i,V_j$就能连在一起,要么就是加入了k点之后能够连在一起

算法:
初始状态就是$M_R$ 然后一个节点一个结点得加进去,三重循环。比原来的$O(n^4)$降低了一个数量级、

例题:


我们用第二个算法做题的格式:
1:列出 R 中的关系对 ,列出节点个数。
2:加入第一个节点,看关系对中有无以第一个节点结尾和开头的元素,将其连接。并在矩阵上标为1。以此类推。比如说上面这个例子,我加入第三个节点,那么我发现$(2,3)$是以3结尾的,$(3,1),(3,4)$是以3开头的,于是我们就可以连接$(2,1),(2,4)$ ; 同理在加入节点4的时候,我发现$(3,4)$是以4 结尾的,$(4,3)$ 是以4开头的,于是$(3,3)$可以在矩阵中标出。
注:有几个节点就加入几次,最后就可以得到传递闭包。
Equivalence relations
如果一个关系同时满足自反性,对称性和传递性这三个性质,我们就把它叫做等价关系

这样的关系有很多。比如等于号,同龄,相似,全等,来自于同一个城市等

Equivalence Classes 等价类


Equivalence Classes and Partitions
Theorem


这个定理说明了对所有a里面的元素的等价类都找出来然后求并集,一定等于A
两个等价类中要么没有公共的元素,只要有公共的元素,那么这两个等价类必然相等
这说明了另外一个概念。
Partition
De nition
一个集合的partition就是由其中的不相交的子集构成的,如下图。
如果这些子集满足partition,那么一定满足以下三点条件

实际上我们可以根据等价类对这个集合求partition
有了等价关系,就有了等价类,所有的等价类构成了集合A的partition
同样如果有一个partition,我们肯定可以导出一个等价类。下面是一个定理:
给定一个partition,有一个等价关系R,他以$A_i$作为等价类
证明其自反性,对称性和传递性即可

例一

例二
有一个比特串组成的集合。
有关系$sR_nt$ ,要么s = t ,要么 前n个字符一样。

Partial orderings 偏序关系
如果一个关系R满足自反性,反对称性,和传递性。那么R就是一个偏序关系
包含关系R的集合S被叫做偏序集,记作(S,R)
偏序关系中的元素满足一下三个条件

A relation R on a set S is a partial ordering if the relation R is reflexice,antisymmetric,and transitive,then (S,R) is called a poset


这里定义了新的关系,叫做偏序关系,a小于等于b
例题5:
Is (S,R) a poset if S is the set of all people in the world and $(a,b)\in R$ ,where a and b are people,if a is not taller than b?
这里我们要区分人和他们的属性,a is not taller than b 确实可以让 a和b的身高相等,但是并不能让a=b,两个人的身高相同不意味着两个就是同一个人!
if a and b do not have a common friend?
很明显这不符合自反性,(a,a) 带入就会自相矛盾。
所以我们判断一个关系是否为偏序关系,必须分清本体和属性的区别和三个性能是否满足。
Comparable
元素 a和b在这个偏序关系,如果a小于等于b或者b小于等于a,那么(a,b)就是可比较的。否则如果不知道哪个小于等于哪个,那么就是不可比较的

比如说在正整数中的整除关系,拿出来两个数3,9 那么3小于等于9,说明这两个元素是可比较的。如果拿出来的是5和7那么它们不可比较的。
所以我们可以知道 正整数上的整除关系并不是一个全序集。全序集就是任意拿出来两个元素都可以比较的。
所以偏序集又可以分为全续集和非全序集

现在我们来看一下字典顺序。我们假设有一个偏序关系是定义在正整数集和正整数集的笛卡尔集上面的,
(a1,a2)是集合中的一个元素。现在我们定义一个关系如下。
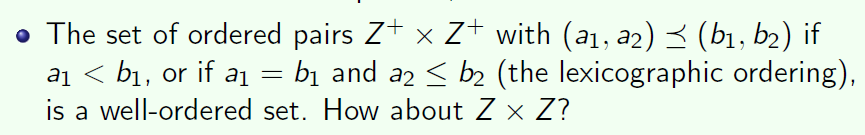
我们称这个关系为字典顺序。为什么要叫字典顺序?因为这就像我们查字典一样,如果我们要查order,我们就直接看o,因为a,b这些开头的 都在o的前面。
这个集合也是一个良序集,良序集的意思就是存在最小的一个元素,这里是(1,1) 那么ZXZ这个笛卡尔集就不是了,因为整数的笛卡尔集不存在最小的元素
我们可以定义两个,也可以定义n个元素
Totally ordered 全序集

全序集 就是一个线性的偏序结构。任何两个元素都能够进行比较。因为我们总是可以知道谁在前谁在后,所以我们也可以把全续集叫做链
如果偏序关系,而且也是个全序集,又满足每一个非空的子集都可以找出来最小的元素,那么我们就可以把这个集合叫做良序集。良序集一定可以拿到第一个元素,找到一个开头的元素。
The principle of well-ordered induction
良序集的应用:数学归纳法。
自然数集是一个良序集。这要这个集基于良序集,那么数学归纳法都是对的,所以我们可以定义字典序集上的数学归纳法。

Lexicographic ordering

这里定义了一个整数和整数的笛卡尔集上的偏序关系,lexicographic就是词典顺序。
比如: Find the lexicographic ordering of these n-tuples:
a) (1,1,2) ,(1,2,1) b) (0,1,2,3) ,(0,1,3,2) c) (1,0,1,0,1),(0,1,1,1,0)
这个方法我们就一个一个比,按照词典顺序排列:
对于a) 1=1 ,1<2 所以 (1,1,2) < (1,2,1)
b) 0=0,1=1,2<3. 所以 (0,1,2,3)< (0,1,3,2)
c) 1>0 所以(1,0,1,0,1) > (0,1,1,1,0)
Hasse diagrams
哈塞图是偏序关系的一种表达关系,而且更简洁
Definition
偏序关系满足自反性,反对称性和传递性。所以一定是每个定点上都有自环。
第一步就去掉所有的自环。
第二步,如果两步可达的顶点,那么就要把一步可达的边给删掉。最后我们要把最小的放在下面,最大的放到上面,这样就可以去掉箭头了。
哈塞图一定是对于偏序关系来说的,上面的结点一定比下面的结点要大

Example
比如下面这一幅图,我们要把它变成哈塞图。第一步去掉所有的环。第二步所有两步并作一步走的边全部都去掉,最后去掉箭头。
Draw the Hasse diagram representing the partial ordering
${(a,b)|a divides b} on {1, 2, 3, 4, 6, 8, 12}$
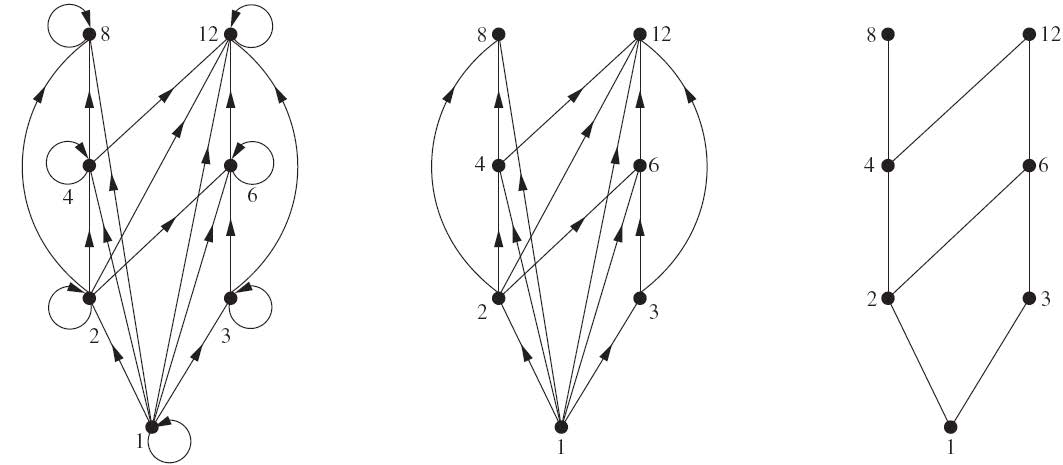
Maximal and minimal elements
极大元和极小元的定义不是最大和最小的元素。还要看看能不能比较。看这里,12和20是不能比较的,所以定义是找不到一个比他更大的元素(找不到一个比它更小的)
这里12,20,25 是极大元,2,5是极小元。没有最大元和最小元

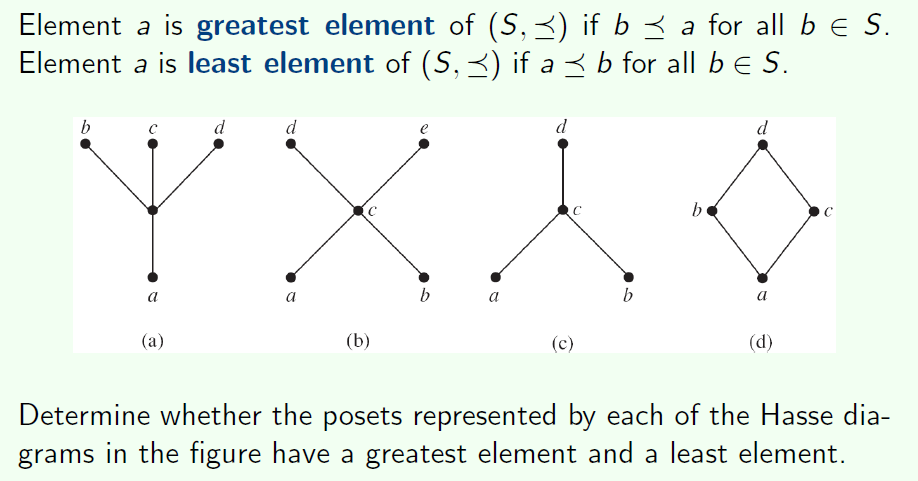
Greatest and least elements
最大元和最小元所有的元素都小于等于或大于等于该元素
下面四张哈塞图。
a是有最小元,但是没有最大元;
b没有最小元,也没有最大元;
c没有最小元,最大元是d;
d既有最小元又有最大元
Upper and lower bounds上界和下界
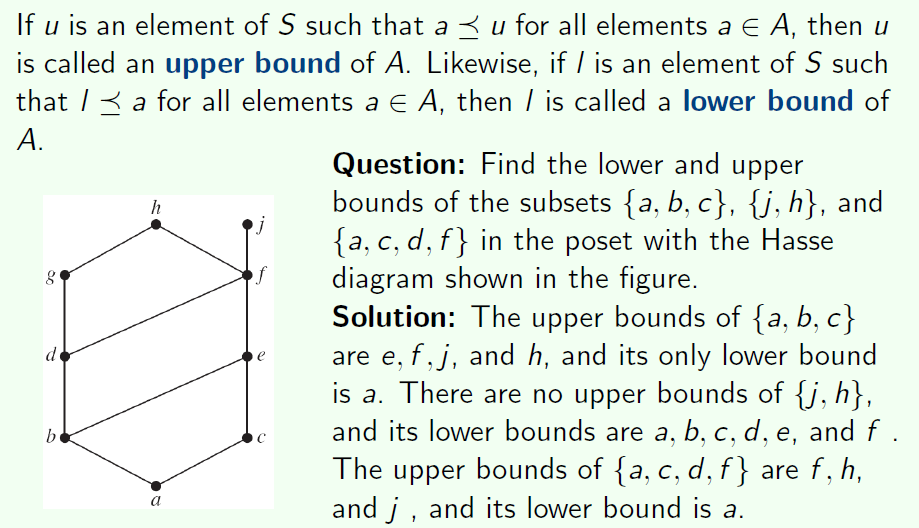
对于一个集合内每个元素都要大或等于的,就是它的上界;对于这个集合内每个元素都要小或等于的,就是他的下界
下面呢我们可以看到
{a,b,c}的上界是 e,f,j,h (因为并没有这样一条 c->d,c->g的路);下界是 a,因为;
{j,h} 没有上界,但是有下界a,b,c,d,e
{a,c,d,f} 的上界是 f、h、j,下界是a
Least upper and greatest lower bounds
Least upper bounds,就是在所有的上界中,它极小
greatest lower bounds,就是在所有的下界当中,它极大
下面这个例子, {b,d,g} 的极大下界就是 b;极小上界就是 g

一个集合的极大下界和极小上界被称为 glb(A) 和 lub(A)
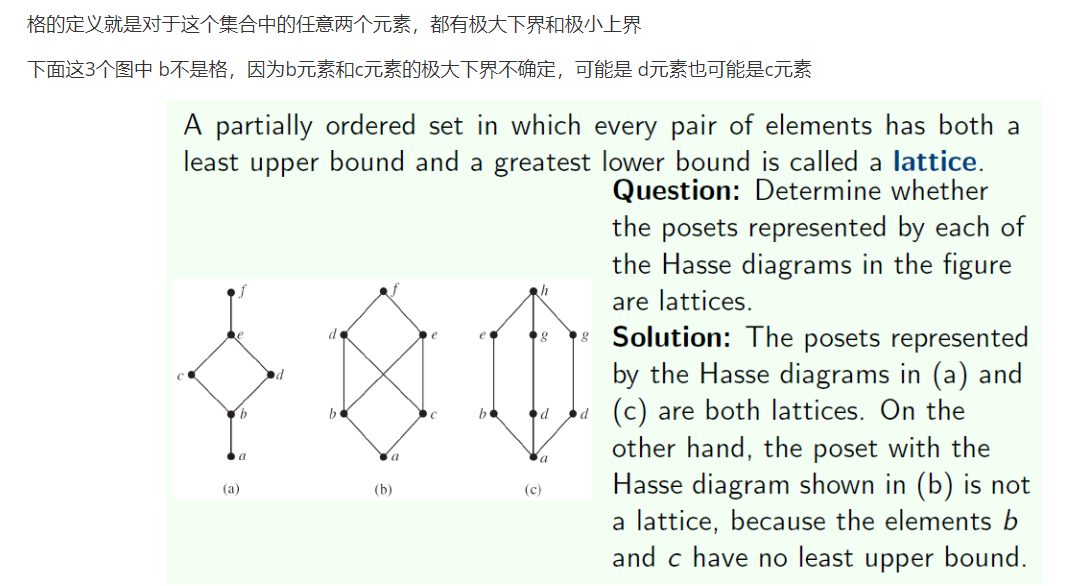
Lattices 格

Topological sorting 拓扑排序

