函数展开成幂级数及其应用

泰勒级数


定理1

定理2

函数展开成幂级数
直接展开法
由泰勒级数理论可知,函数f(x) 展开成幂级数的步骤如下:
- 求函数及其各阶导数在x=0 处的值;
- 写出麦克劳林级数,并求出其收敛半径为R
- 判别在 收敛区间(-R,R) 内 $\lim\limits_{n->\infty}R_n(x) $(余项)是否为0
展开为幂级数,也可以说是展开成麦克劳林级数
例题
1

2

3.




4.

5.

间接展开法
利用一些已知函数的展开式和幂级数的运算性质,将所给函数展开成幂级数




小结
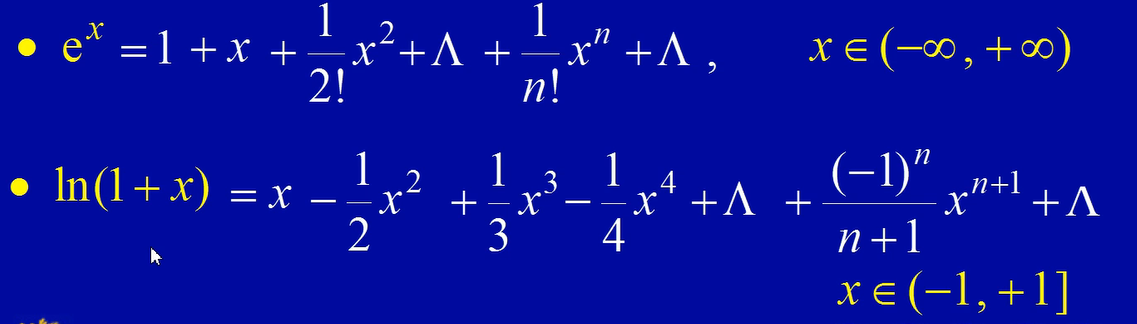

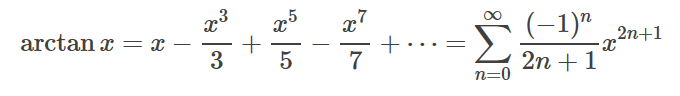
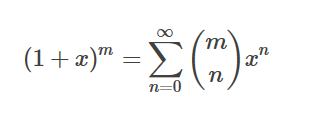
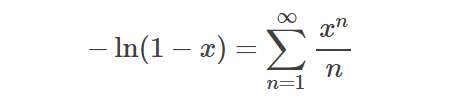
我们可以利用这个拓展的二项式定理解决很多问题
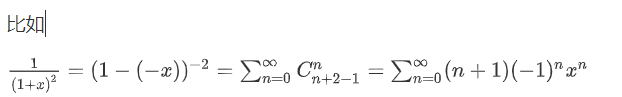
又比如

解题步骤
展开为幂级数
低难度
如果是三角函数,那么通过降幂,转化等,化成 sin kx 的形式
如果是个复杂的分子式,我们需要因式分解,然后转化成 1/x+1 或者1/1-x 的形式
高难度

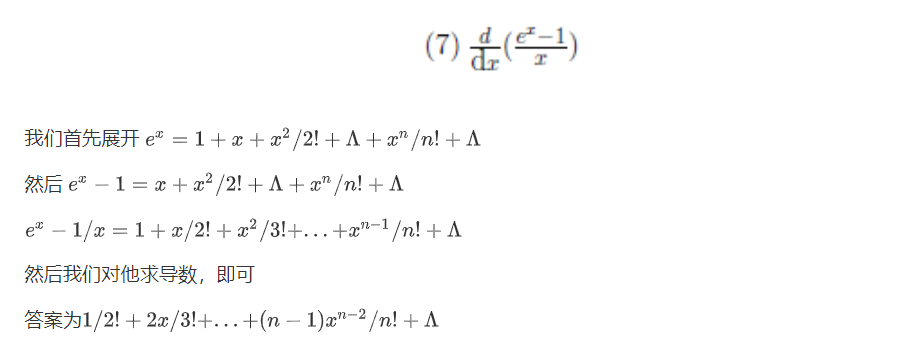
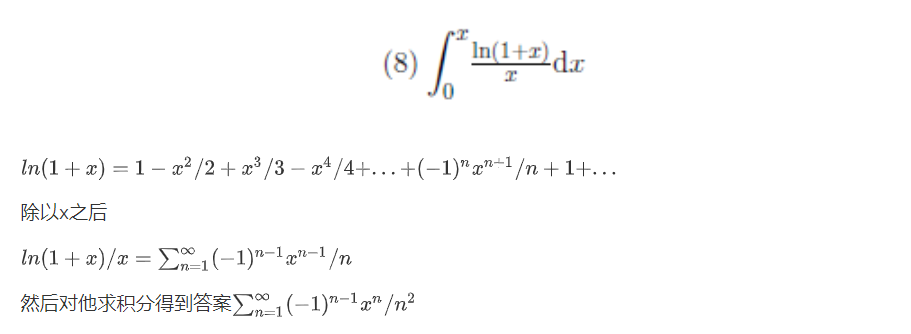
(9) $(1+x)ln(1+x)$
幂级数展开与和函数
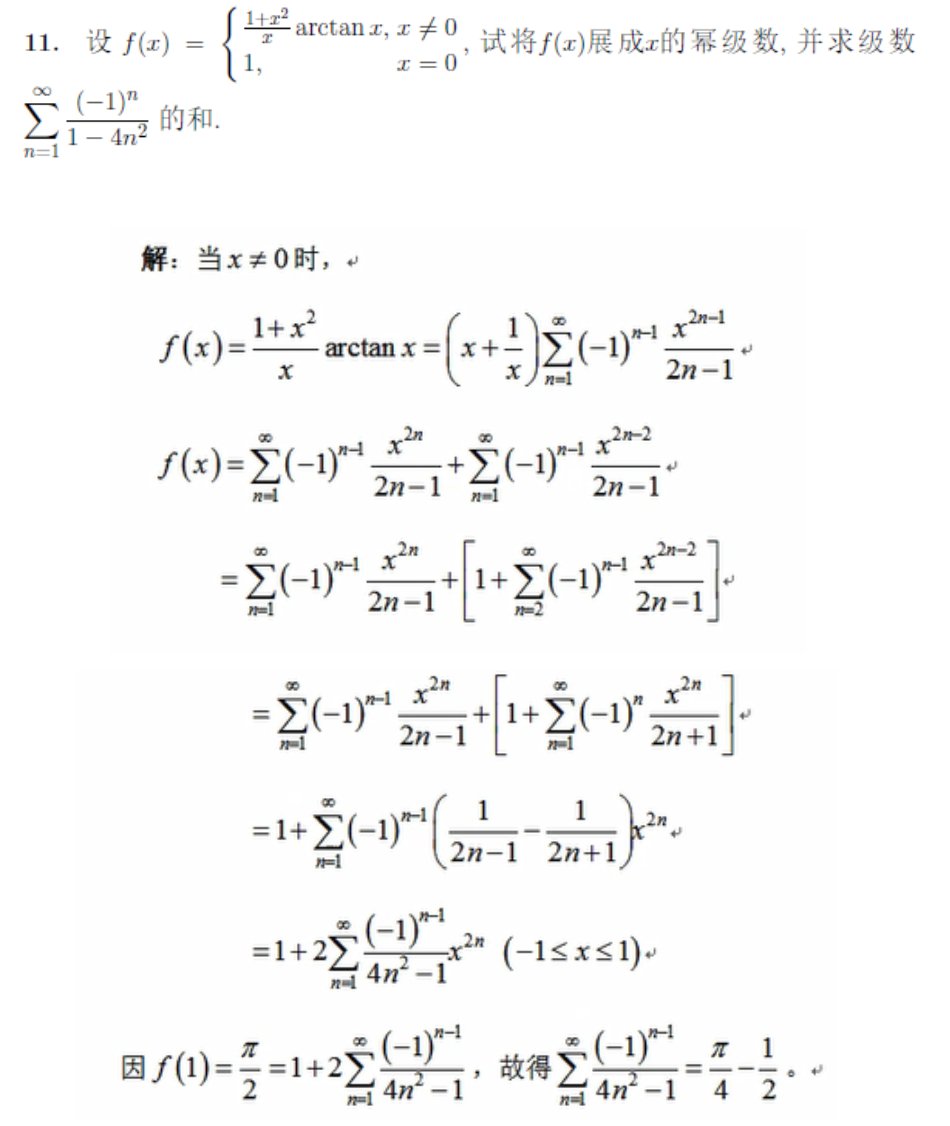
展开为XXX的幂级数


