B树
概要
二叉搜索树的搜索效率和树高成正比关系,通过减少二叉搜索树的高度,可以提高搜索效率今 平衡二叉树可以减少树高,但是仍然不够彻底,因为每个结点只含有—个关键字,树 高仍然是$O(\log n)$, 能否继续压缩树高, 使其更加扁平化呢?
如果—个结点不限于存储—个关键字,可以包含多个关键字和多个子树,既保持二叉搜索树的特性,又具有平衡性,这样的搜索树称为多路平衡搜索树 如图所示平衡二叉搜索树比晋通的二叉搜索树高度低,而多路平衡搜索树的树高更低,更加扁平化, 搜索的效率更高。
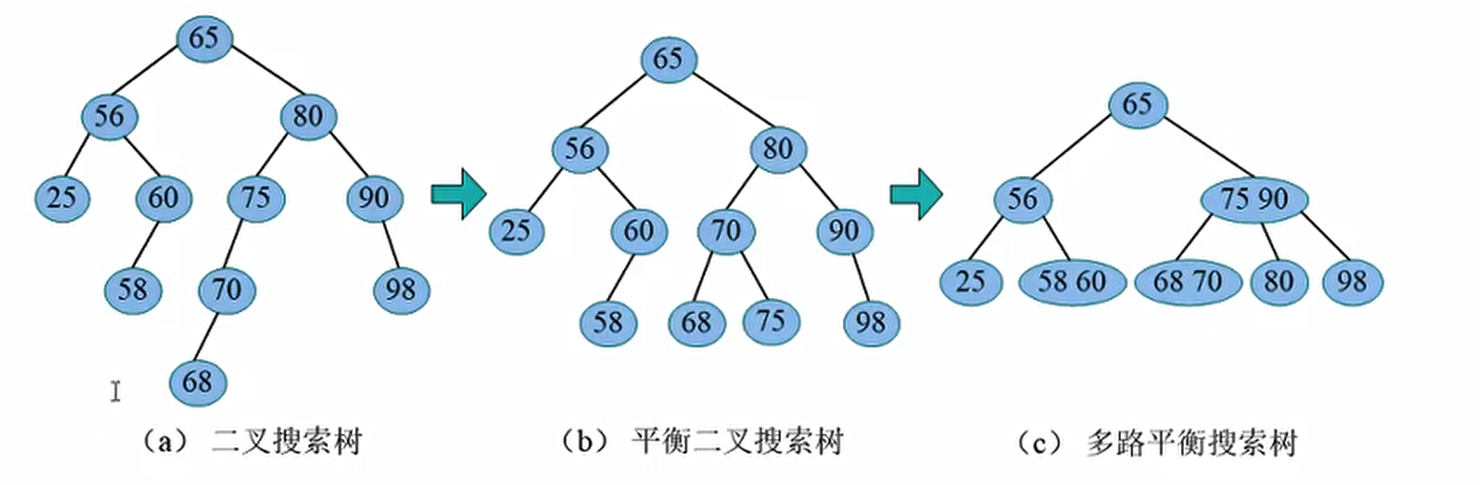
那么是不是越扁平就越好呢?再压缩下去, 就变成—个包含所有结点的树根了! 这样的效率反而会退化,因为这就相当于线性查找了,又退化成了 $O(n)$
事实上并非如此,多路平衡搜索树主要用于大规模数据的分级存储搜索,将内存的 “ 高速度 ” 和外存的 ”大容量” 结合起来,提高搜索效率。众所周知,内存的访问速度是很快的, 而外存的访问速度则慢5-6个数量级, 数据规模巨大时,无法全部放入内存,数据全集往 往放在外存中,如果频繁地访问外存,则搜索的效率降低。如何减少外存操作呢?
外存访问时,访问一个数据和访问一段连续存储的数据,时间差别不大。因此可以用 “ 大结点 ” 代替多个单个结点, 一个 “ 大结点 ” 包含多个连续存储的数据,作为一个整体, 进行一次外存访问。将这个 “大结点 ” 调入内存后, 再进行多次内存操作, 例如顺序查找或折半 查找。 与外存访问相比, 内存操作的成本很小。
一个“大节点”到底到底包含多少个数据元素合适呢?主要取决千不同外存的批量访问特性。例如,可以根据磁盘扇区的容量和数据元素的大小计算出一个一个“大节点”包含数据元素的个数。若一个大结点包含255 个数据元素,那么1G个数据元素,每次查找需要4-5次外存访问。而如果使用平衡二叉搜索树(AVL树) ,则每次查找需要30次外存访问
多路平衡搜索树,又称为B-树,或者B树。一颗m阶B-树,或为空树,或满足以下特性
- 每个结点最多有m棵子树
- 根结点至少有两棵子树;
- 内部结点(除根和叶子之外的结点)至少有$\lceil m/2\rceil$棵子树;
- 终端结点(叶子)在同—层上,并且不带信息(空指针), 通常称为失败结点。
- 非终端结点的关键字个数比子树个数少 1

例如,3阶B-树,其内部节点的子树个数$2\leq k\leq3$ ,所以又称为2-3树。也就是说每个节点有1-2个关键词,2-3棵子树,所有的叶子都在最后一层,如图
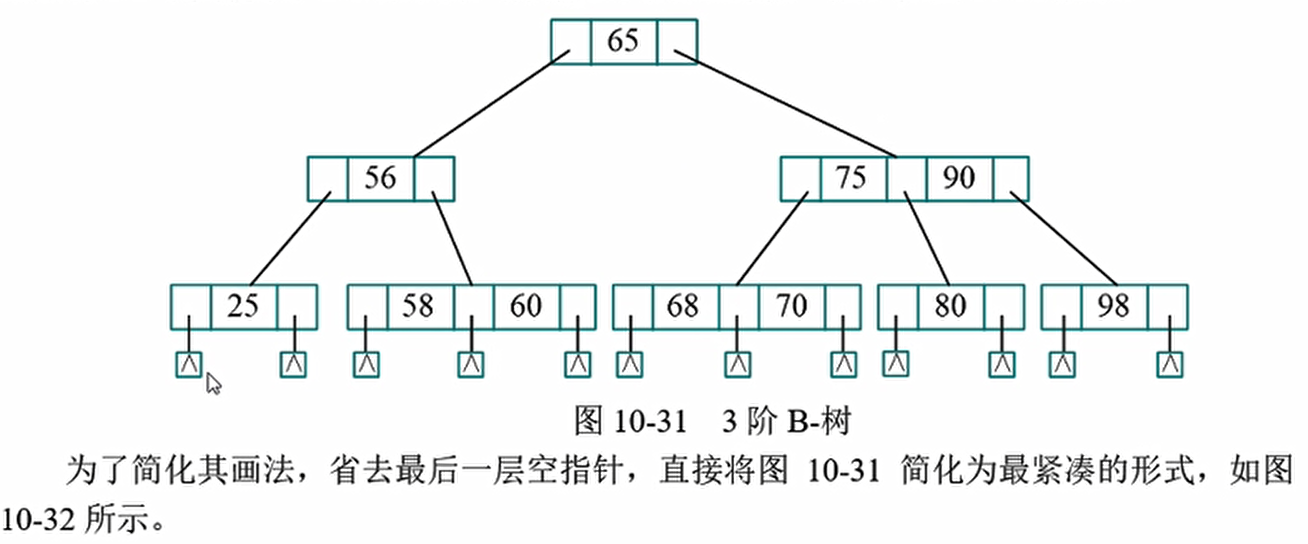
注意指针的方向
如果我们要查询20,那么比65小,左子树;比56小,左子树;比25小,那么说明查找失败-失败节点就是这么命名的
B树具有平衡、有序、多路的特点,所有的叶子都在最后一层,因此左右子树的高差为0,体现了平衡的特性。B树具有中序有序性,即左子树<根<右子树。多路是指可以有多个分支,m阶B树的节点最多可以有m个分支。所以也可以成为m路平衡搜索树
查找插入删除操作和树高成正比关系,因此线分析树高,然后详解B树的查找插入、删除等基本操作
树高与性能
一颗含有n个关键字的m阶B-树的最大高度是多少呢?
首先我们要看每层至少有多少个结点,因为结点越少,高度越大。根据定义,根节点至少有2棵子树,那么第二层至少有2个节点,除了根之外,每个非叶子节点至少有 $\lceil m/2\rceil$ 棵子树,每个子树对应一个节点,因此第三层至少有 $2\lceil m/2\rceil $(取上限)个节点,以此类推, 第 h+1层,至少有 $2\lceil m/2\rceil^{h-1}$ 个叶子节点
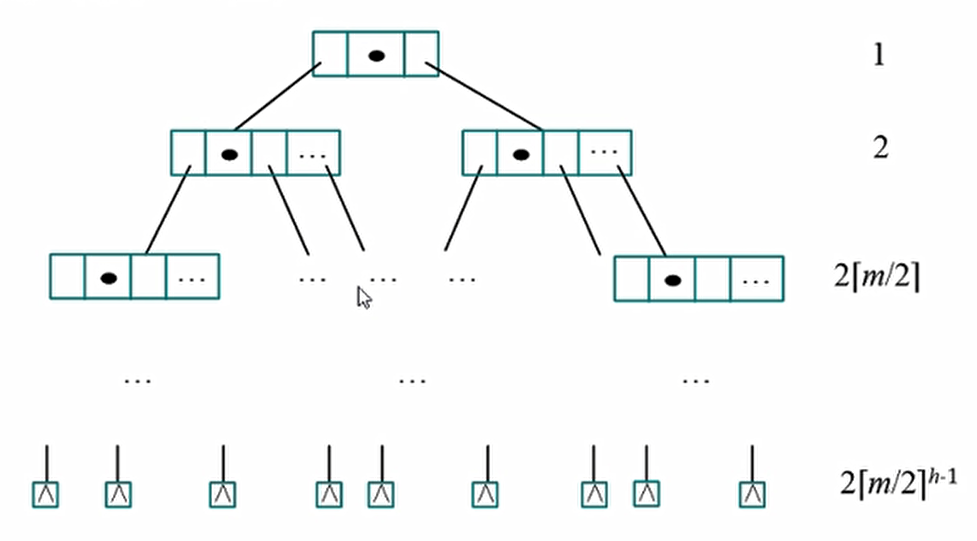
叶子结点为查找失败的空指针,n个关键字又n+1种查找失败的情况,即:
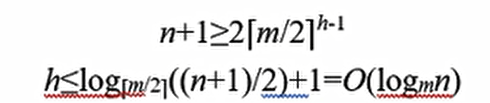
$\lceil O(\log_mn)\rceil$就是树高,后面分析的B树的查找、插入、删除等基本操作的时间复杂度时可以利用该结果进行分析
比如说5阶B树,53个结点,最大的树高就是$O(\log_327)+1$ =4
还可以算最小的树高,那么每个节点都包含$m-1$个结点,最多会有$m$个分支,那么第$h+1$层就有$m^h$ 个结点。所以 $n+1<=m^h $ , 即 $\log_m(n+1)\leq h$ 放到刚才的例子当中 $\log_554$ 向上取整,也就是3层
因此,最短树高: $h = \lceil \logm(n+1)\rceil$ , 最长树高: $h=\lfloor \log{\lceil m/2\rceil} ((n+1)/2)+1\rfloor$
查找
B树的查找和二叉搜索树的查找类似,不同的是需要从外存调入结点,然后在结点内查找(—个结点可能包含多个关键字 )
首先将根结点作为当前结点, 在当前结点的关键字中查找目标, 若查找成功, 则返回 。否则通过判断进入下—层的结点, 若该结点不是叶子(空指针), 则将其从外存调入内存作为当前结点, 重复查找过程。在任何时刻,通常只有当前结点在内存中,其他结点放在外存中, 需要时才会调入内存。
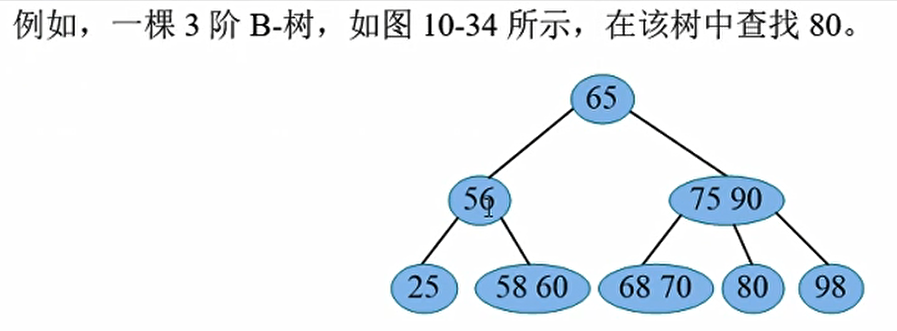
首先和65比,比65大,那么和右子树比,和75,90比,在中间,那么在中间的指针种查找,所以找到了80
忽略掉内存查找的时间(内存的查找时间很短,可以忽略不计),我们执行了3次外存查找
算法分析
B-树的查找时间包括将结点从外存调入内存和在内存中当前结点查找两个方面。结点间的跳转作为—次外存访问,结点内的查找作为多次内存操作,因为外存和内存操作时间相差巨大, 因此结点内的内存操作忽咯不计,只需要考察在查找的过程中,访问了多少个结点即可 查找最多从根边问到叶子, 即树的高度$O(\log_mn)$, 含有n个关键字的m阶B-树, 因此。m阶B-树查找的时间复杂度为$O(\log_mn)$
插入
插入操作, 首先要在B-树中查找合适的插入位置。 因为关键字不允许重复, 如果查找成功,则不进行插入操作,返回。如果查找失败,则将关键字插入到失败结点的双亲结点中。
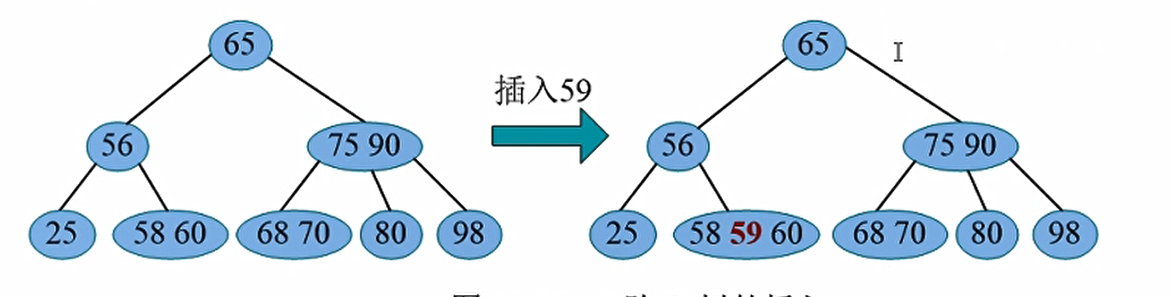
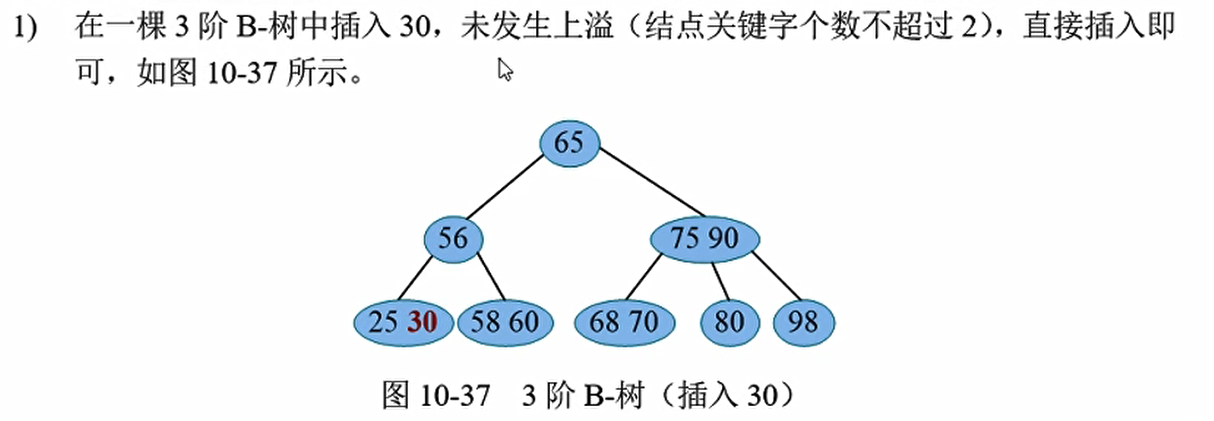
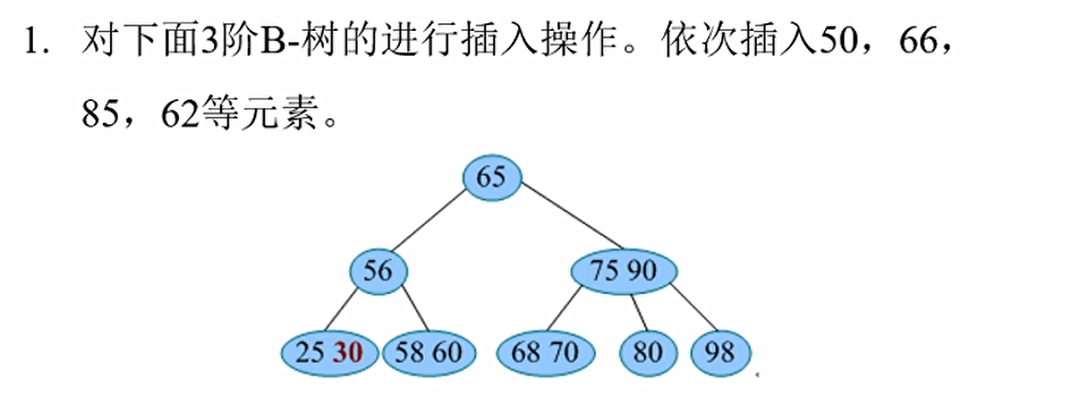
例如, 在 棵 3 阶 B-树中插入 59, 首先查找位置, 59 大于 58 小于 60, 而 58 和 60 之间的子树为空指针, 查找失败, 将 59 插入失败节点父亲的位置。 如图 10-35 所示。
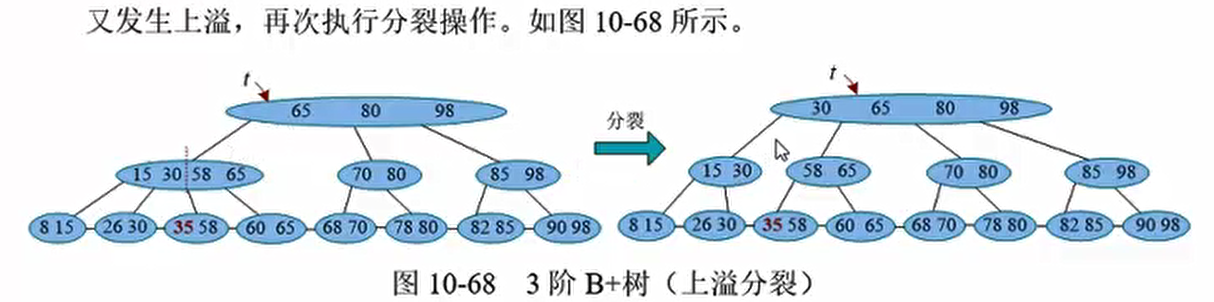
上溢
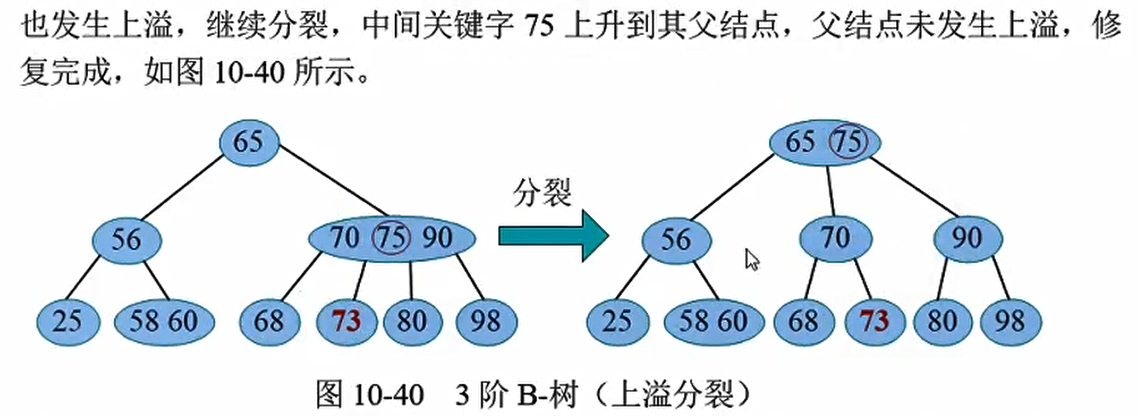
但是m阶B-树主结点的关键字个数不能超过m-1, 插入关键字后, 如果仍然满足此条件, 那么插入操作完成。 如果插入后, 关键字个数为m (超过了m-1), 则发生了一次上溢。 帣要进行分裂操作解除上溢, 使该结点及整棵树重新满足m阶B-树的条件。(因为这是一个3阶B树,每个结点的关键字的个数为1,2。显然这个超过3个节点了,所以这就发生了上溢)
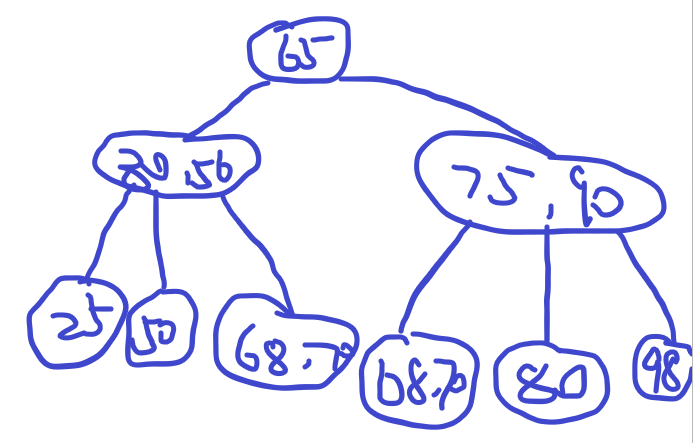
刚刚发生上溢的结点V, 插入之前满足条件(关键字个数小于等于m-1), 插入之后大于m-1, 因此V结点现在恰好有m个关键字。 将该关键字分裂操作:取V结点中间的关键字$K_s (s=m/2)$, 将$K_s$上升到其父结点P, 左右两部分作为$K_s$的左右孩子, 如图10-36所示。
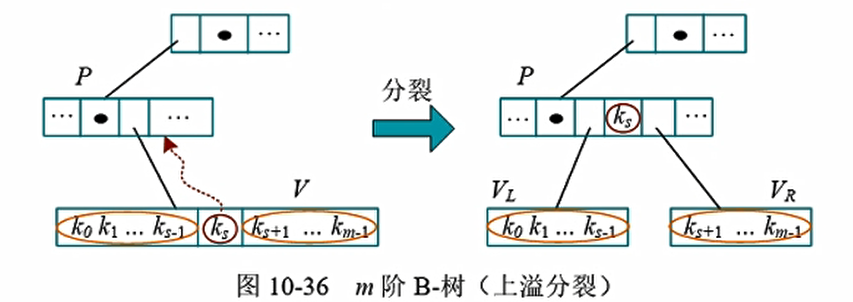
这里,把中间的关键字59往上提
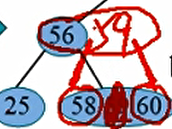
这里父亲没有发生上移,否则还要继续往上分裂,一直可以分裂到树根。最后让树高加一
分裂操作将上溢结点的中间关键字位上升到其父结点,如果其父结点这时也发生上溢,则继续分裂操作,一直向上传递, 录远到达树根。
位上升到其父结点P后, 可分为3种情况:
第一种情况
p结点未发生上溢, 修复完成
第二种情况
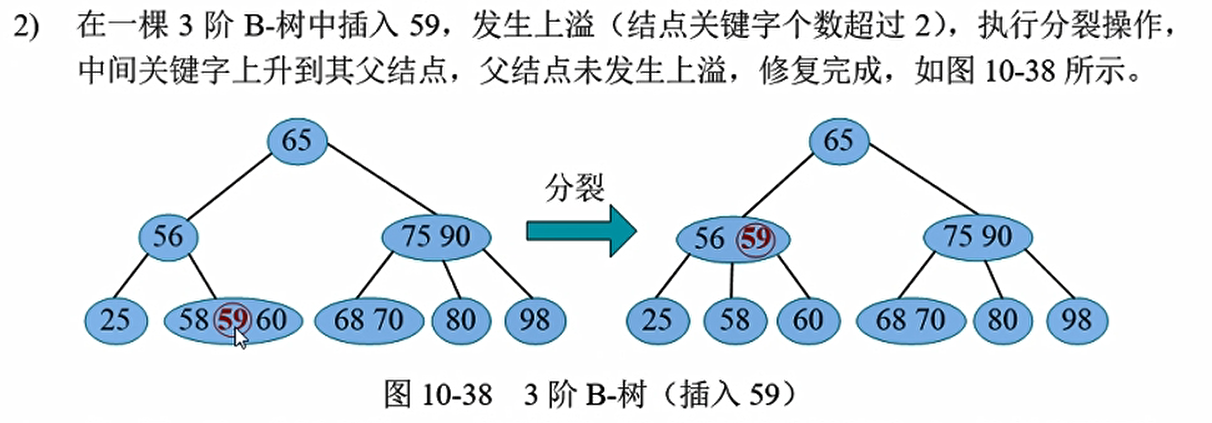
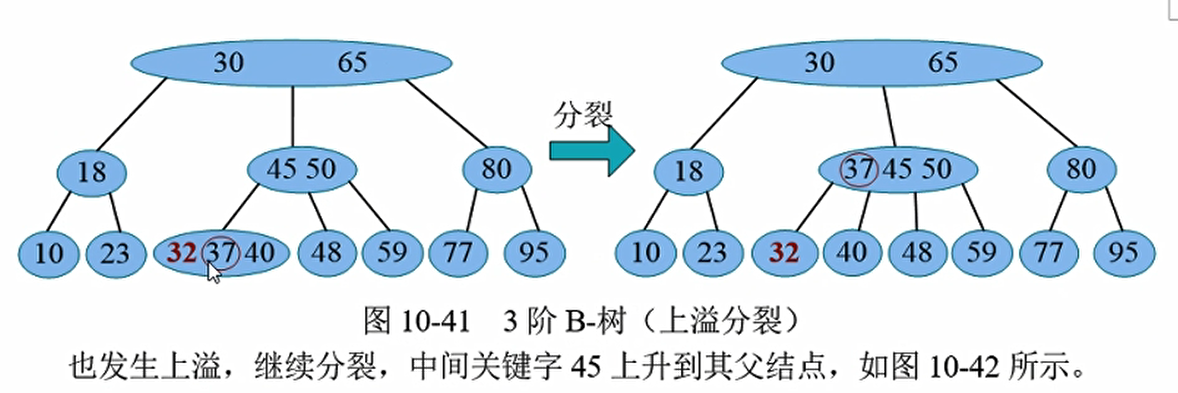
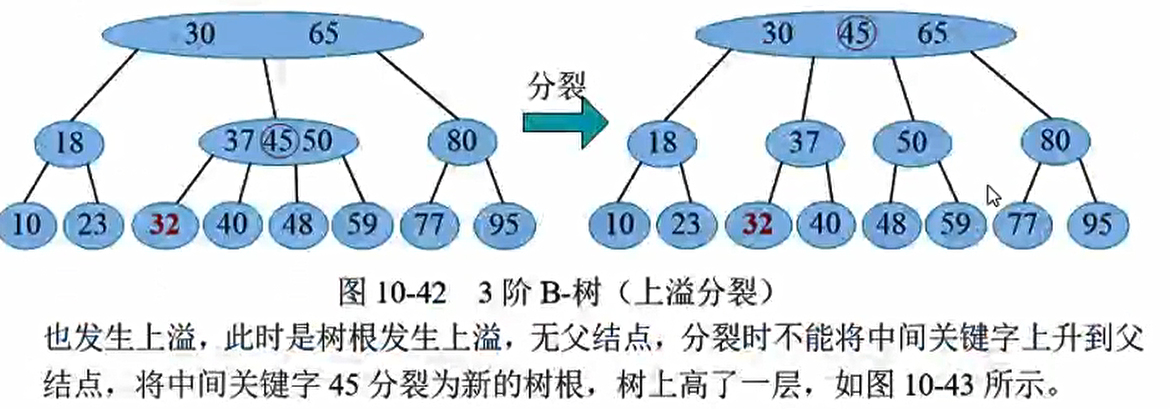
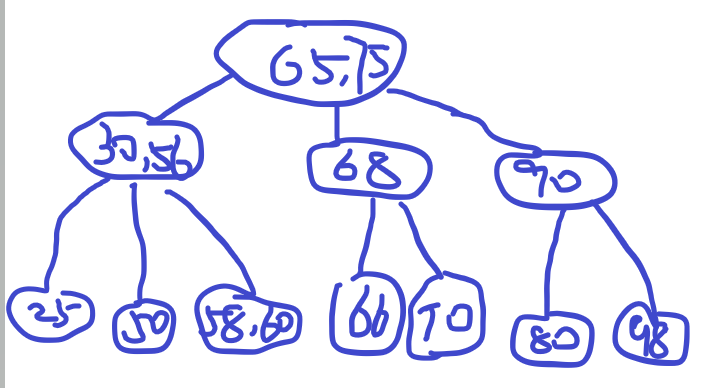
p结点发生上溢,执行分裂操作,一直向上传递,在到达树根前不再发生上溢, 或到达树根但树根未发生上溢, 修复完成。
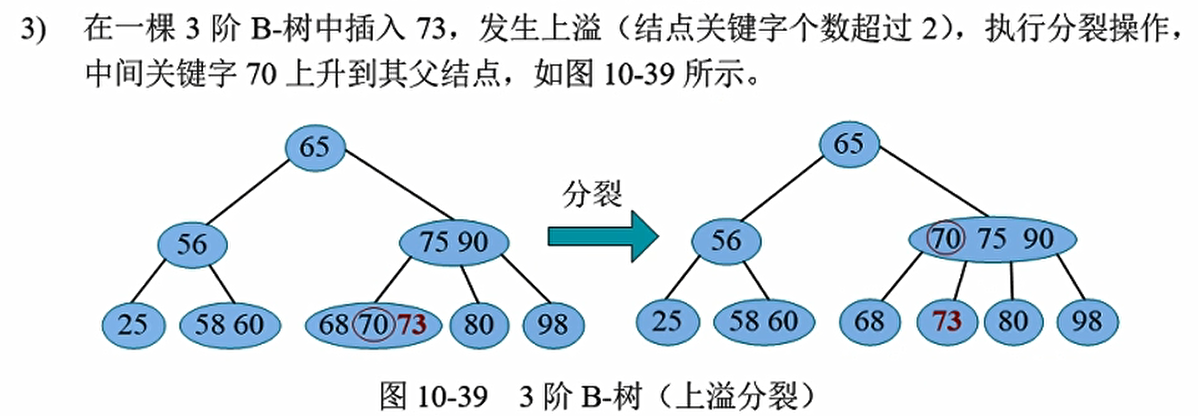
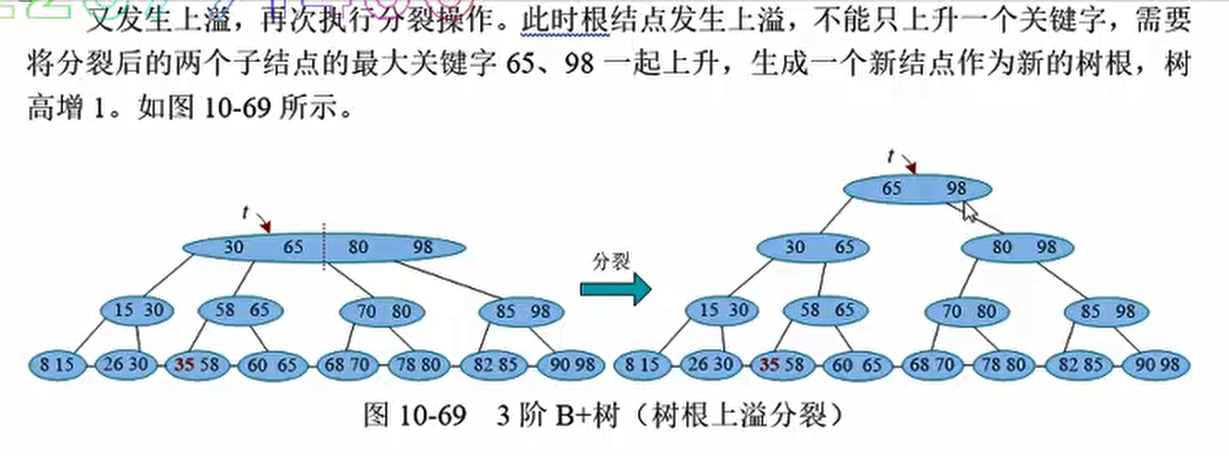
第三种情况(特殊)
上溢一直传递到树根,树根也发生上溢,那么将树根分裂,根节点中间关键字分裂成新的树根,修复完成,此时树的高度增加了1

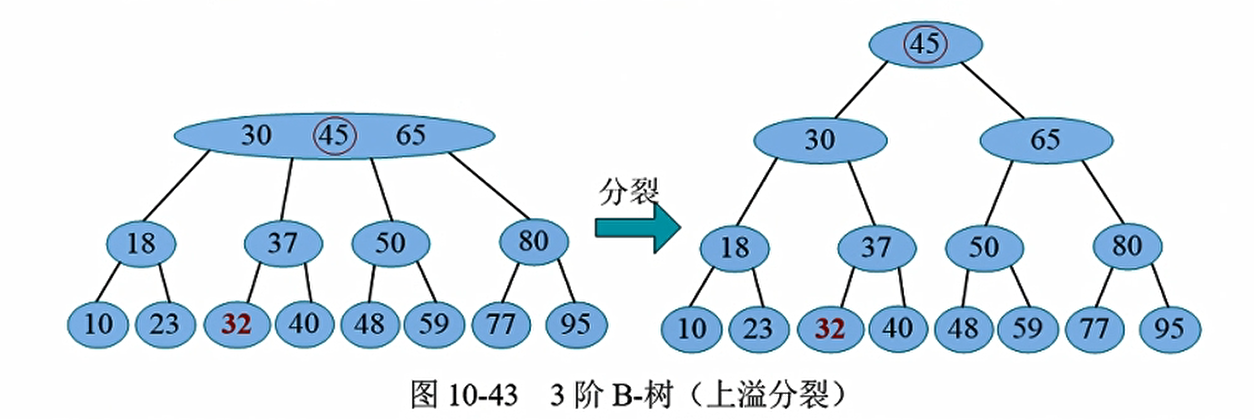
只有树根发生上溢的时候,B-树才会长高一层,其他情况,树高不变。树根分裂的时,新的树根只有一个关键字和两棵子树,这也是B-树定义中,特别是定义树根的原因
算法分析:
含有n个关键字的m阶B-树,插入操作除了查找插入位置(需要$O(\log_mn)$时间) 之外,如果发生上溢,需要分裂操作,分裂操作不会超过树的高度$O(log_mn)$,因此,插入操作的时间复杂度为$O(\log_mn)$
现在给我们一串数字,那么我们就可以先查找再看看有无上溢来新建一个m-阶B-树了
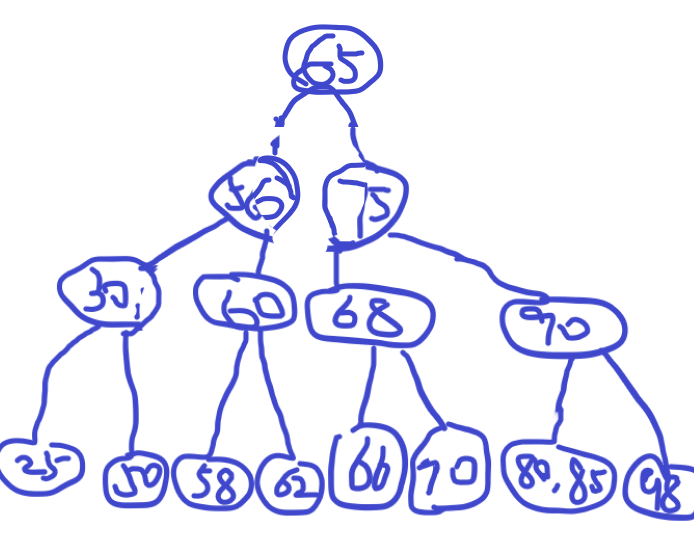
删除
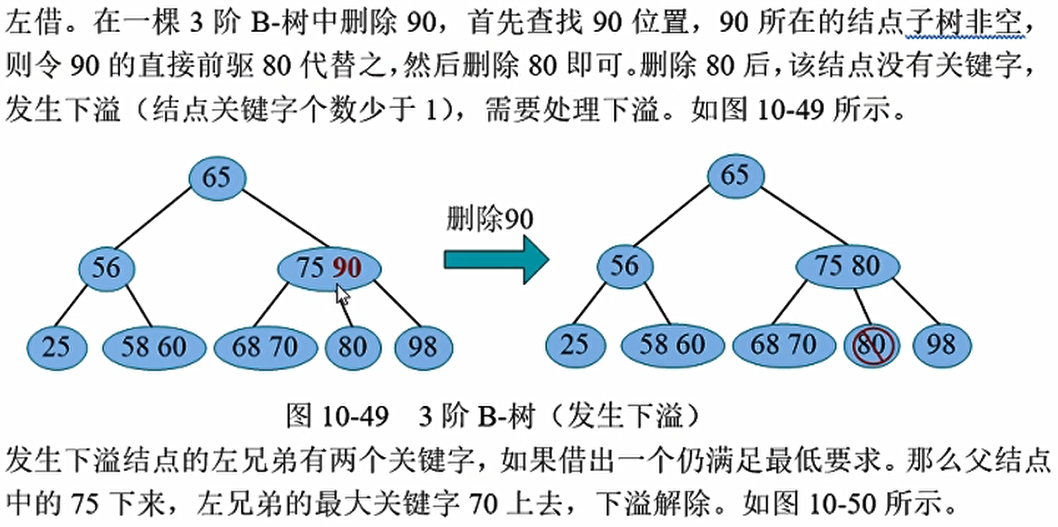
删除操作, 首先要在B-树中查找待删除关键字的位置。 如果查找失败,则不进行删除操作, 返回。如果查找成功,则执行以下删除操作。如果待删除关键字的子树非空,则需要像二叉搜索树一样, 令该关键字的直接前驱(或直接后继)代替待删除关键字, 然后删除其直接前驱(或直接后继)即可。直接前驱(或直接后继)的子树一定为空。因此只需要处理待删除关键字的子树为空的情况即可。
例如,在一棵3阶B-树中删除75,首先查找75位置,75所在结点的子树非空,则令75的直接前驱70代替之,然后删除70即可。
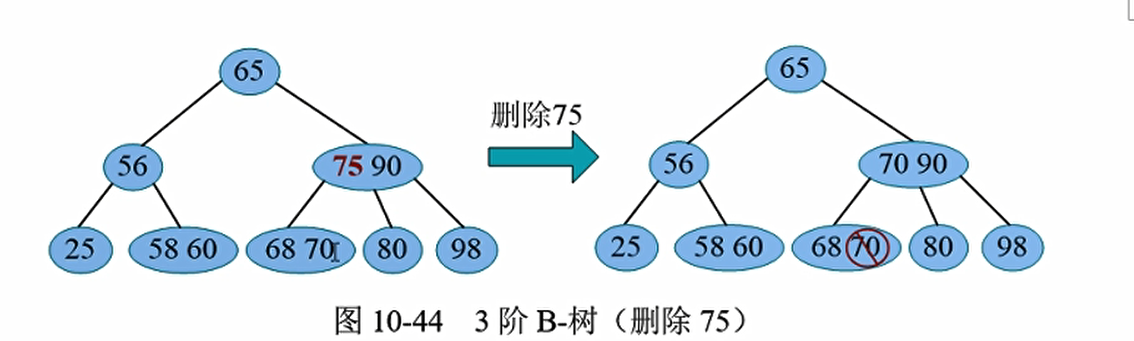
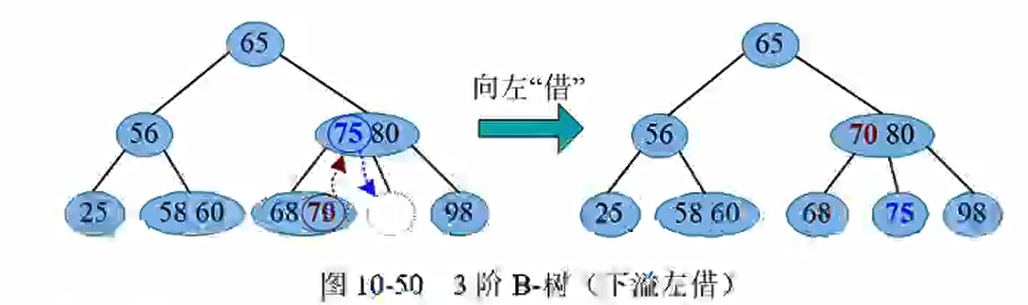
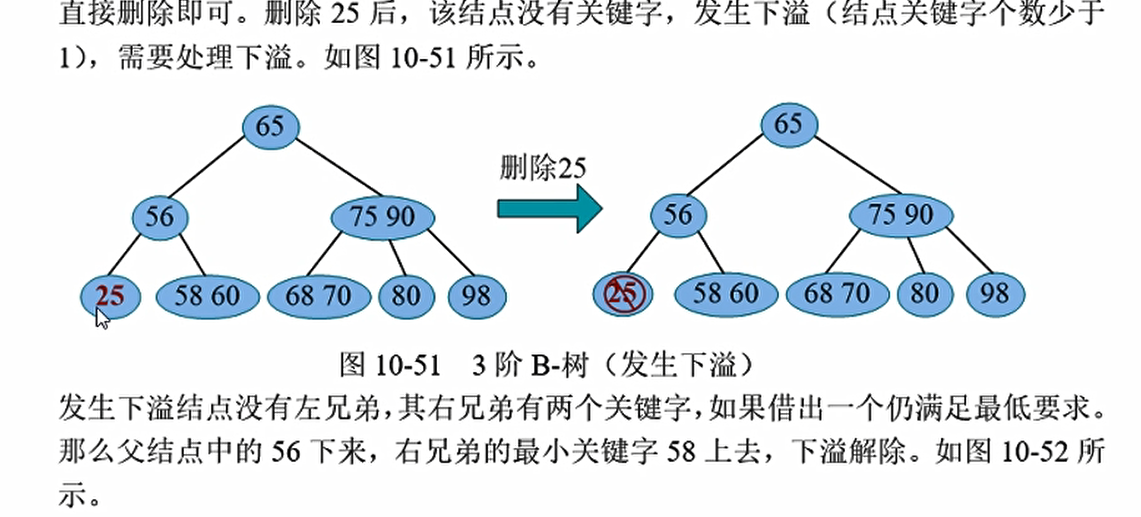
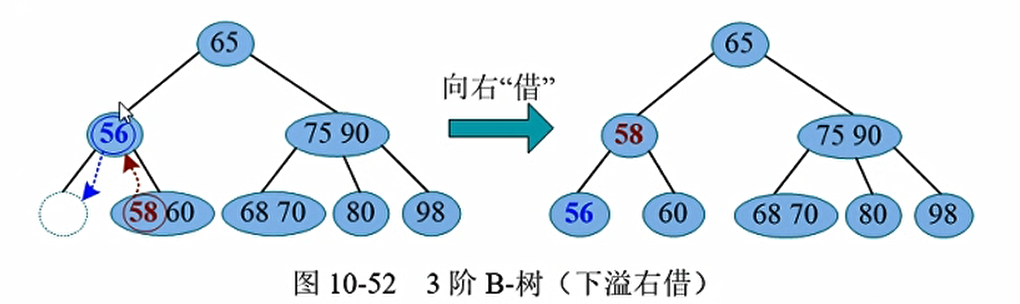
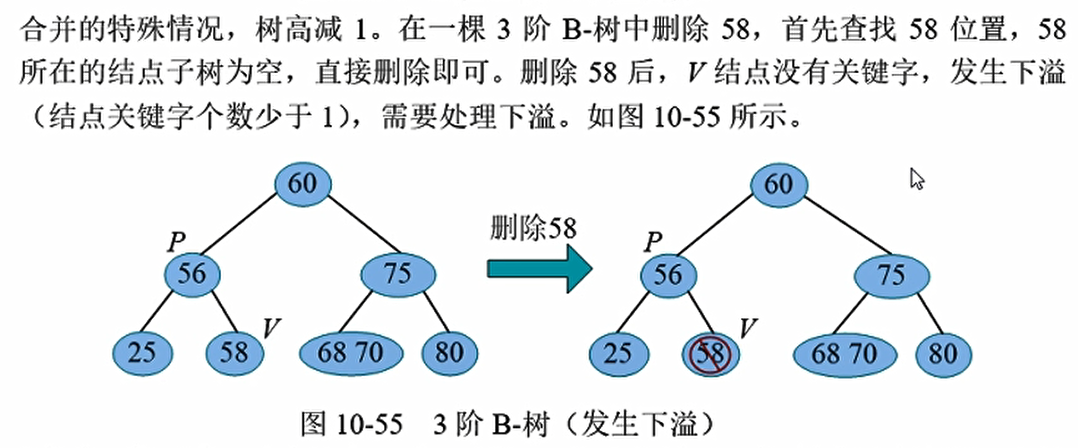
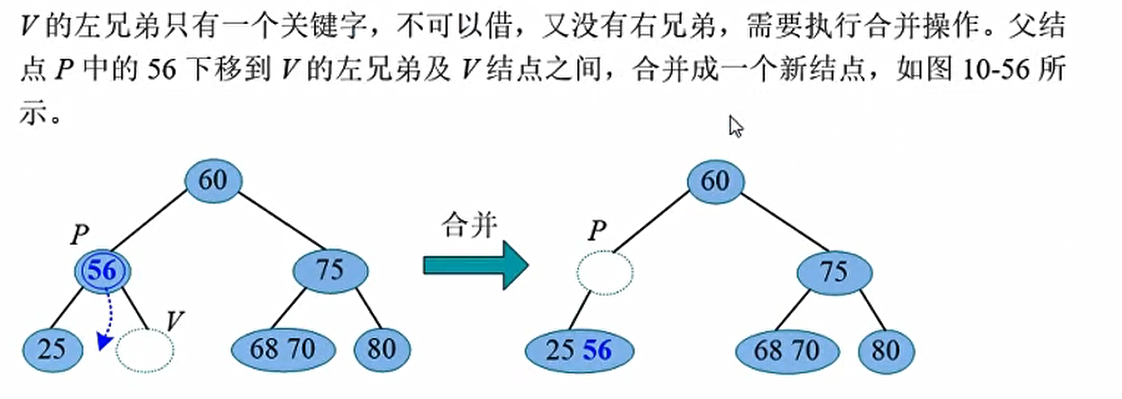
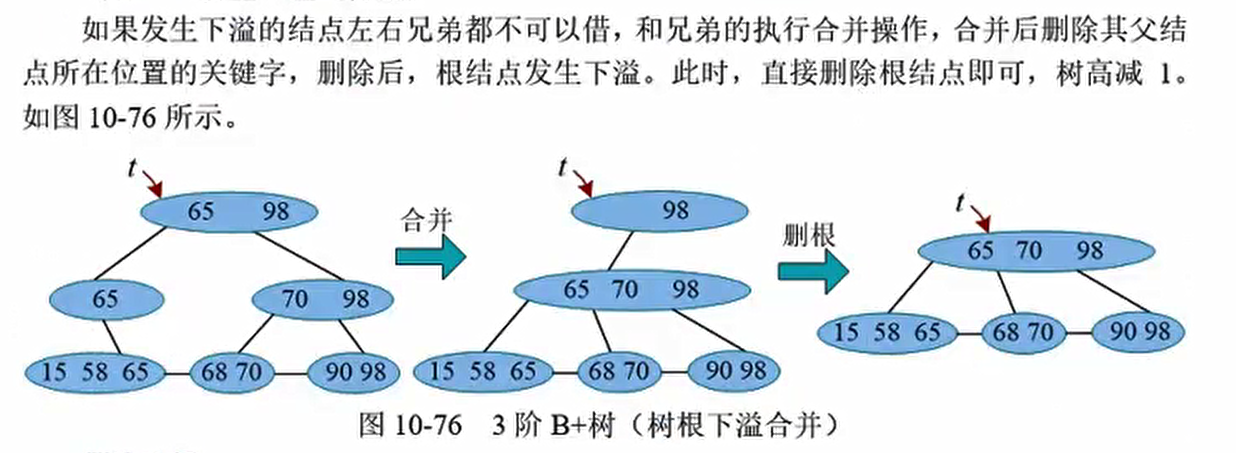
那么如果拿直接前驱去代替它,是可以的,但是我们一定要保证删除后的结点仍然至少拥有1个关键词,如上图,删掉了70还有68;但是如果删掉了节点以后该节点小于$\lceil m/2\rceil-1$,那么我们就发生了下溢, 需要相关操作解除下溢,使该结点及整棵树重新满足 m阶B-树的条件

下溢
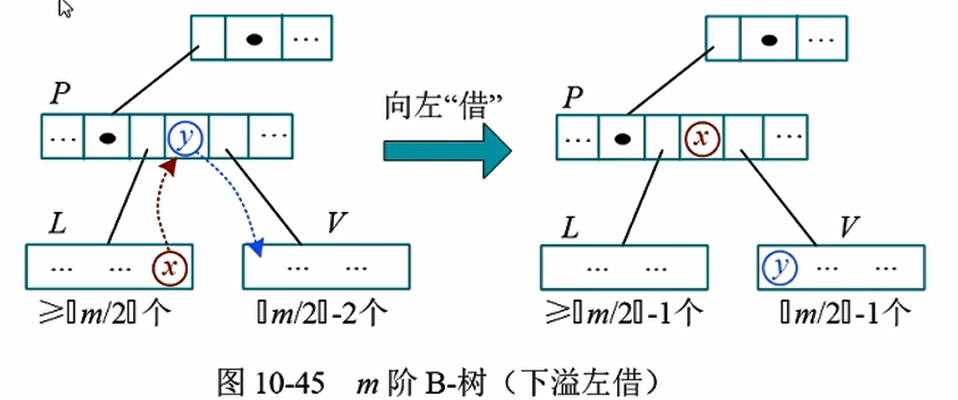
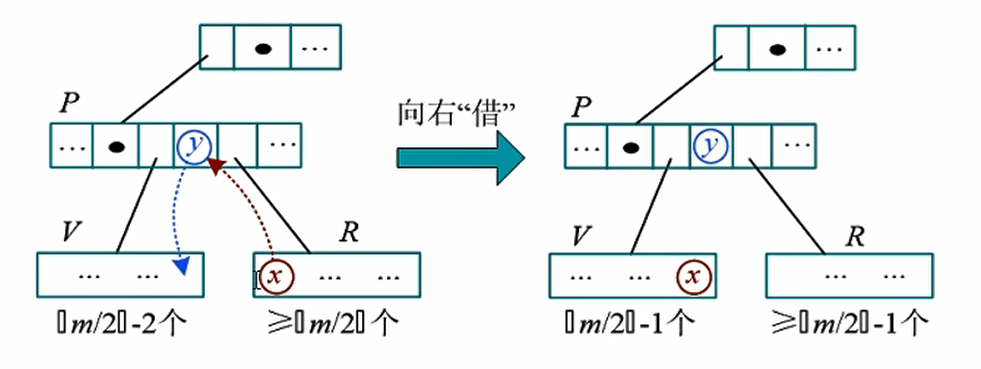
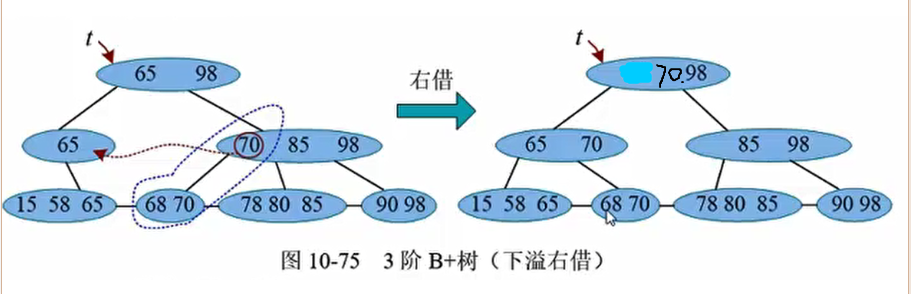
考察下溢结点V的左右兄弟,下溢处理分为3种情况:左借、右借、合并
左借

右借

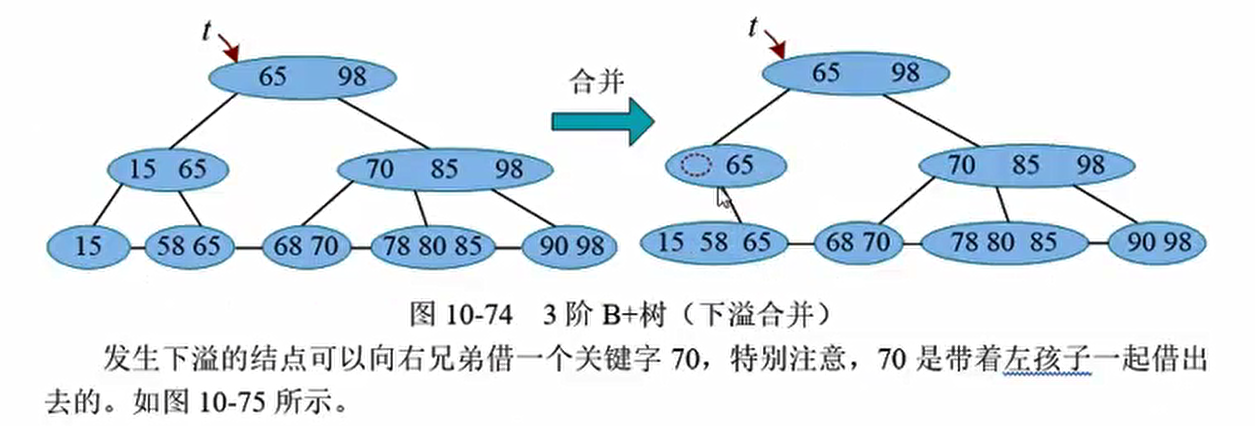
合并

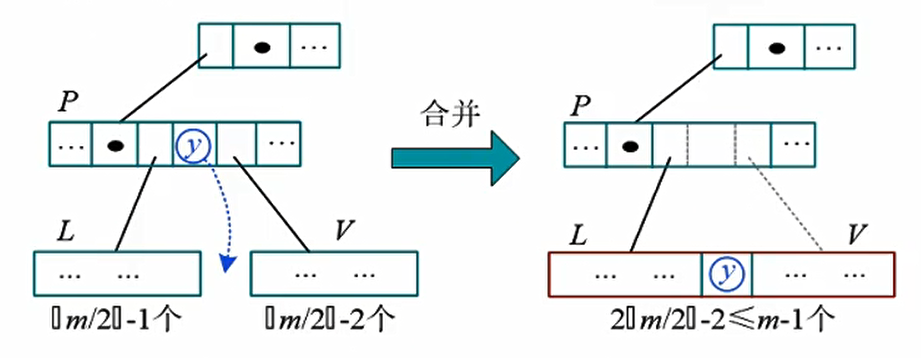
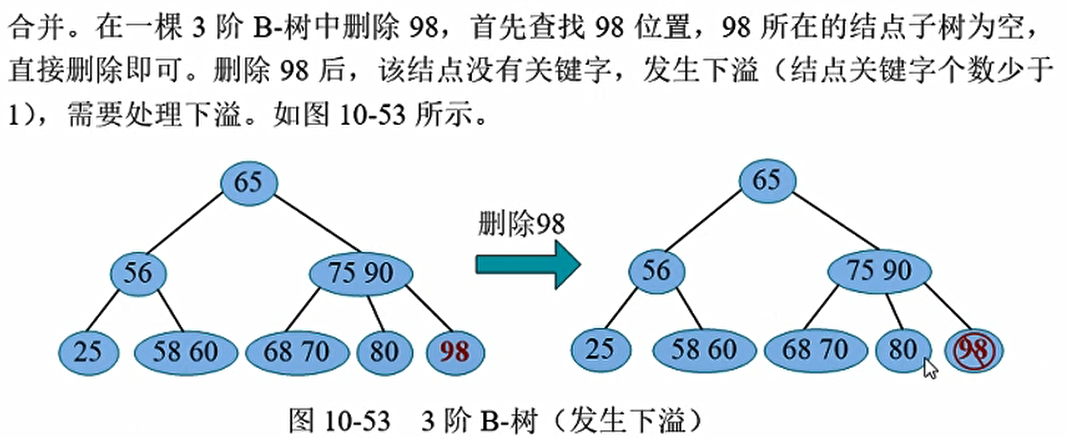
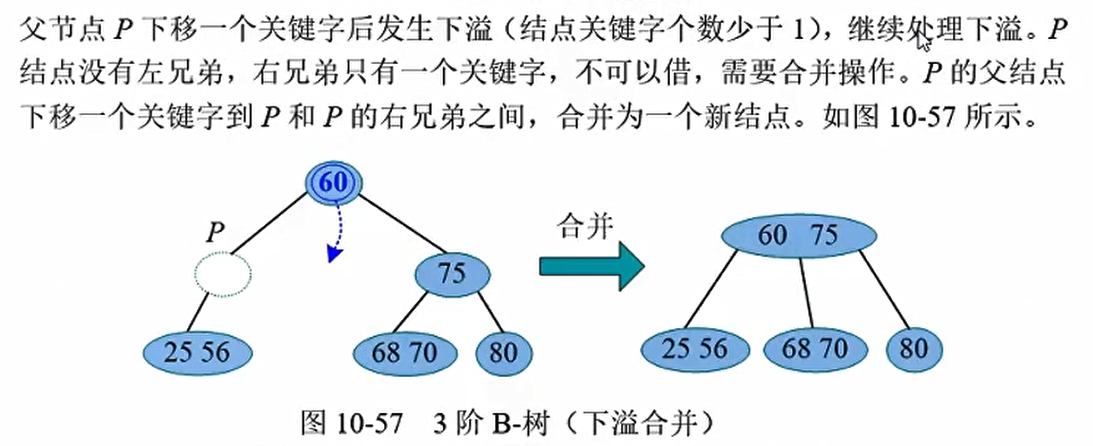
发生下溢结点的左兄弟只有一个关键字,不可以借,也没有右兄弟。需要执行合并操作。父节点中的90下来,将左兄弟及下溢结点粘合成一个新的结点,父节点下移一个关键字后仍然满足条件,下溢解除。
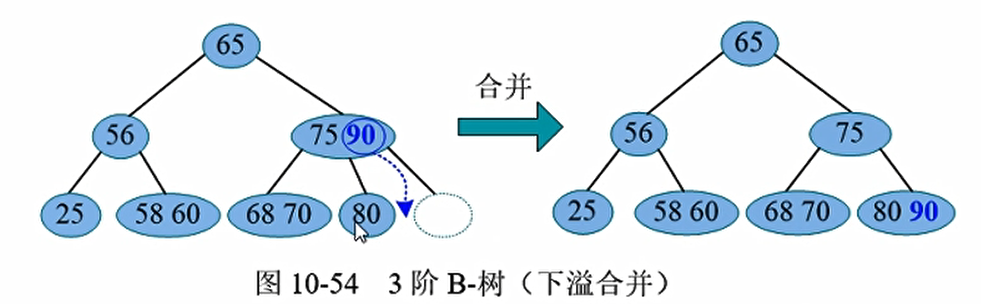
特殊情况,树高减一
算法分析
含有n个关键字的m阶B-树,删除操作除了查找插入位置(需要$O(\log_mn)$时间) 之外,如果发生下溢,需要左借、右借或合并操作,合并操作不会超过树的高度$O(\log_mn)$,因此,删除操作的时间复杂度为$O(\log_mn)$
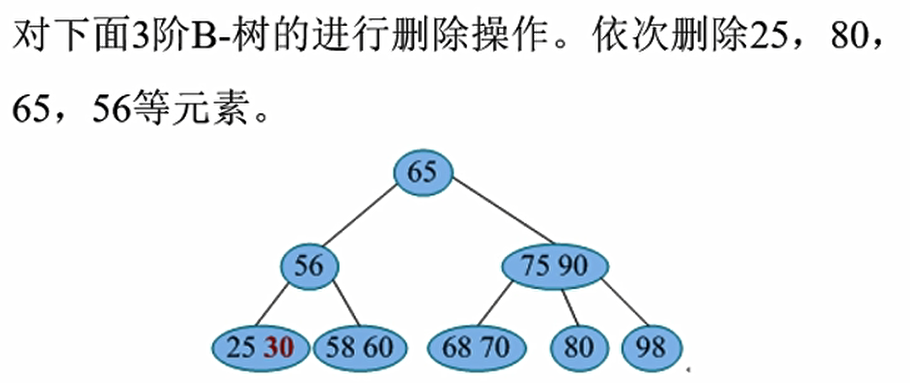
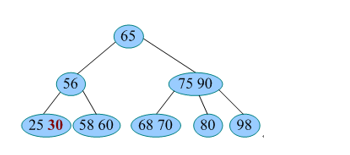
- 删除25,节点中还有30,符合条件,直接删除即可
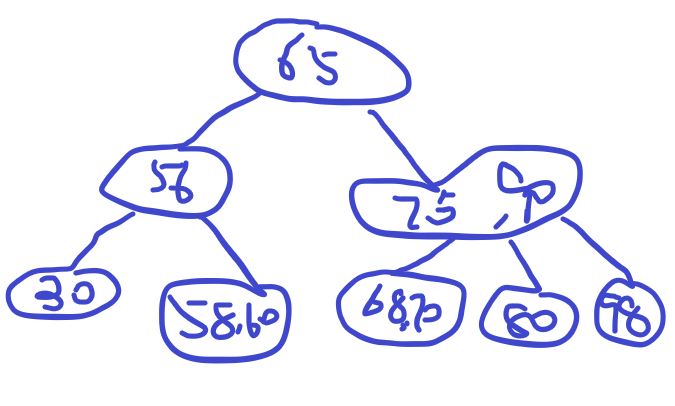
- 删除80, 节点为空,此时左兄弟有两个节点,可以实行左借策略,把70放上去,把75放在原来80的位置
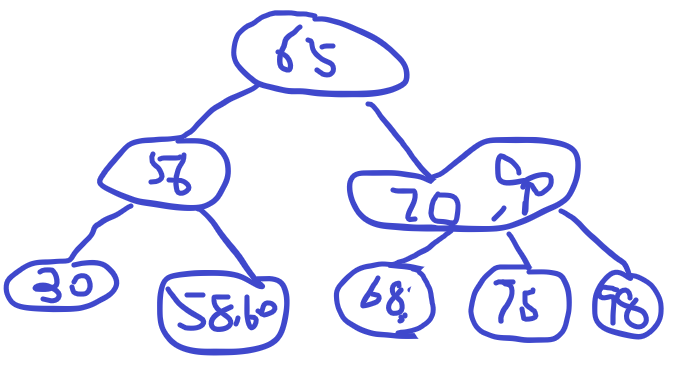
- 删除65,先用最大前驱60代替65的位置,然后删除60,节点数据个数符合条件,不用进行借、合并操作
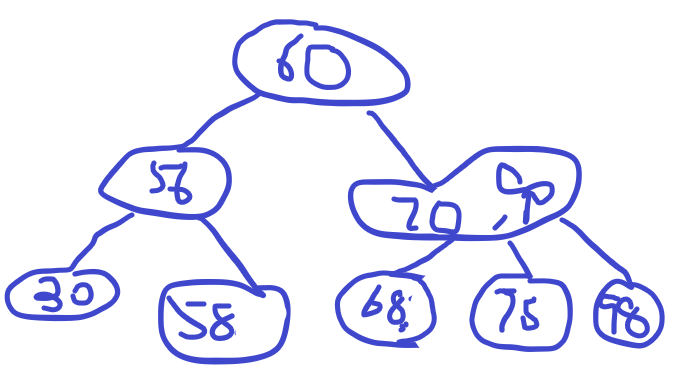
- 删除56,节点为空,右兄弟有两个(70,90), 执行右借,70提上去,60移到56的位置
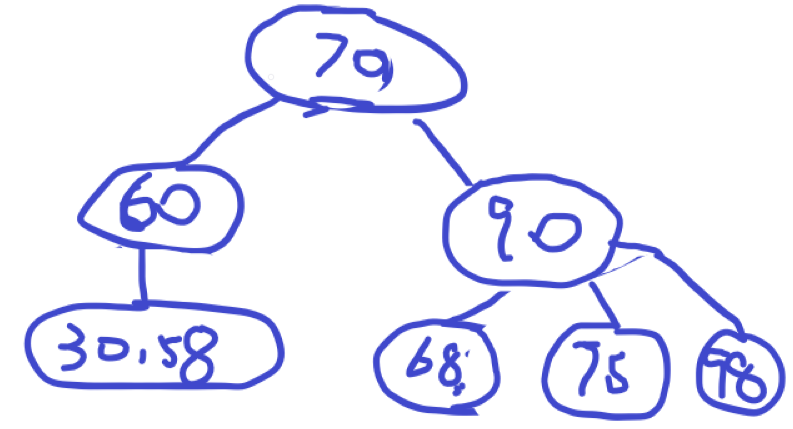
含有10亿个节点的3阶B-树的高度仅仅在19-30(根据上面提到的公式$\log_mn = \log_210^9 = 30$)之间,最多只需要访问30个结点就能够在10亿个键中进行任何查找、插入、和删除操作
习题
具有n个关键词的m阶B树,应有多少叶节点? 即考察我们查找失败的可能性,即 n+1种,因此,由n+1个叶子节点
考察节点数:高度为5的3阶B树至少有多少节点,至多有多少结点?这里是3阶B树,节点内的关键字最少1个最多2个,因此节点数最少的时候,3阶B树的形状类似于一个满二叉树。此时高度为5的B树至少有 $2^5-1=31$ 个节点; 由于每个节点最多又m棵子树,所以当节点数最多的时候,3阶B树的形状类似于满三叉树,节点数为$(3^5-1)/2 = 121$
含有n个非叶节点的m阶B树,至少包含又多少个关键词?m阶B树每个节点包含的关键词最少是 $\lceil m/2\rceil -1$ ,根节点至少包含两颗子树、一个关键词,因此至少包含$(n-1)(\lceil m/2\rceil -1)+1$ 个关键词
利用B树做文件索引的时候,若假设磁盘页块的大小是 4000 B, 指示磁盘地址的指针需要5B,现有20000000个记录构成的文件,每个记录为200B,其中包括关键词5B
试问这个采用B树作索引的文件中,B树的阶数应为多少? 假定文件数据部分 没有按照关键字有序排列,则索引部分需要占用多少磁盘页块?
根据B树的概念,一个索引节点应适应操作系统一次读写的物理记录大小,其大小应取不超过、但最接近一个磁盘页块的大小。假设B树为m阶,一个B树节点最多存放m-1个关键词(5B) 和对应的物理地址(5B)、m个子树指针(5B) 和一个指示磁盘地址种的实际关键字个数的整数 (2B) ,则有:
$(2(m-1)+m)\times 5 +2 \leq 400$ 解得 $m\leq 267$
一个267阶B树的索引节点最多可以存放m-1=266 个索引项,最少可以存放 $\lceil m/2\rceil -1=133$ 个索引项。因此,一共$n=2\times10^7$ 个记录,每个记录占用200B,每个页块可以存放20个记录,则全部记录将会分布在$p = 1\times 10^6$ 个页块种,最多需要占用$1\times 10^6/133=7519$ 个磁盘页块作为B树索引,最少需要 $1\times 10^6/266 = 3760$ 个磁盘块作为B树的索引
B+树
B+树是B-树的变种, 更适用于文件索引系统。 从严格定义上,B+树已经不属于树, 因为叶子之间有连接, 树是不允许同层结点有连接的。
一棵m阶B+树, 或为空树, 或为满足以下特性:
- 每个结点最多有m棵子树。(这一点和B树是一样的)
- 根结点至少有两棵子树。(这一点和B树是一样的)
- 内部结点(除根和叶子之外的结点)至少有$\lceil m/2\rceil$(取上限)棵子树。(这一点和B树是一样的)
- 终端结点(叶子)在同—层上,并且不带信息(空指针), 通常称为失败结点。 (很重要)
- 非终端结点的关键字个数与子树个数相同。(和B树不一样,B树的关键字个数比子树少一个)
- 倒数第二层结点(非空叶子)包含了全部的关键字, 结点内部有序且结点间按升序顺序链接。
- 所有的非终端结点只作为索引部分, 结点中仅含子树中的最大(或最小)关键字
例如,一棵3阶B+树,其内部节点的子树个数$2\leq k\leq 3$,关键字的个数也是 $2\leq n\leq3$ 如下图,一般有两个指针,一个指向树根,一个指向倒数第二层关键字的最小节点(最后一层全是空的!)
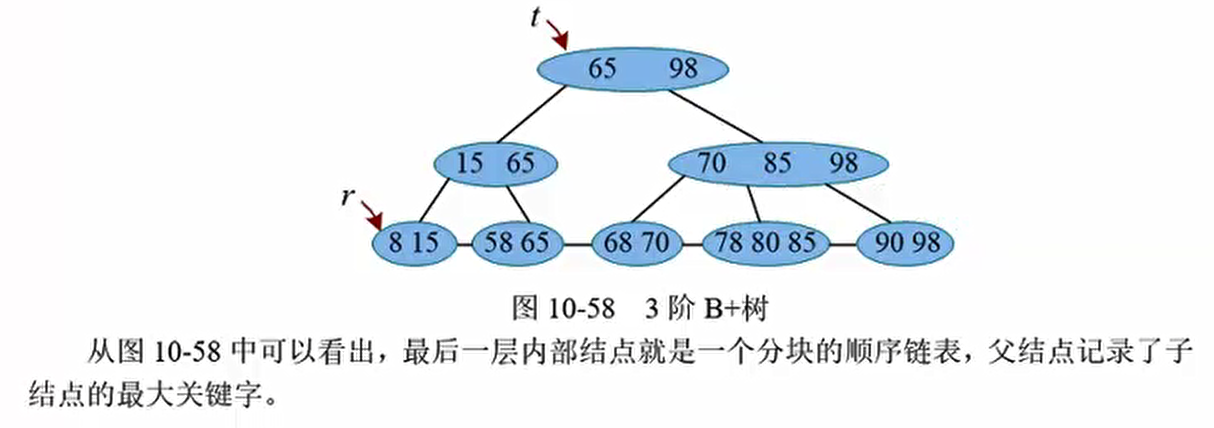
B+树的查找
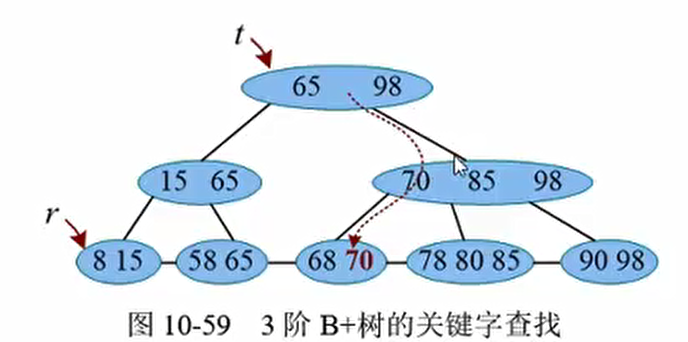
B+树可通过两种方式的查找,可以利用 t 指针从树根向下索引查找,也可以利用r指针从最小关键字向后顺序查找。尽管如此,仍不建议顺序查找,因为其时间复杂度为$O(n)$, 索引查找效率要高得多。
若从树根向下查找,则首先在根结点中查找,然后在子树中查找,即使查找成功,也会继续向下,直到最后一层。也就是说,每次查找都要走一条从树根到叶子的路径,时间复杂度为树高$O(\log_mn)$

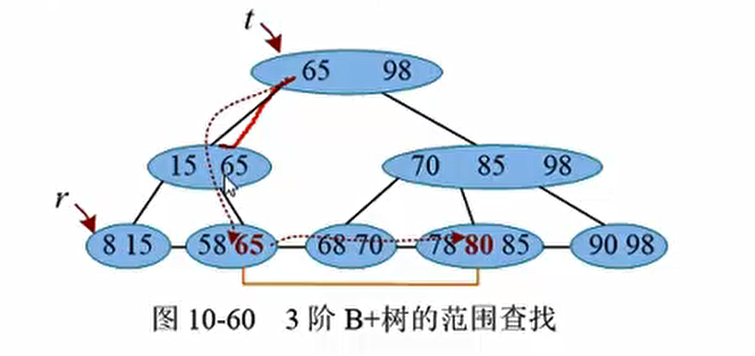
B+树不仅支持单个关键字查找, 还支持范围查找。 例如, 查找范围在[a, b]之间的关键字, 首先查找a所在的位置, 从根到最后一层, 查找等于或大于a的关键字, 如果找到, 则继续在a所在的结点查找,如果未发现大于b的关键字,即可以沿该结点的最后一个指针查找下一个结点, 直到找到一个等于或大于b的关键字停止。
例如,在一棵3阶B+树中查找[60-80]之间的关键字
- 首先查找60所在的位置,从根到最后一层,查找等于或者大于60的关键字,未找到60;
- 沿着60顺序查找,找到比它大的关键字65
- 继续在该节点中查找,在下下个节点中找到了等于80的关键字,查找成功。
B+树的插入
m阶B+树的插入, 仅在最后一层结点插入, 因为除了最后一层结点, 其他非终端结点都表示索引。 又因为m阶B+树的关键字个数要求不超过m, 如果插入后结点的关键字个数超过m, 则发生上溢, 要分裂操作。 只不过分裂时, 和B树的分裂不同, 上升到父结点的关键字, 子结点中仍然保留。
刚刚发生上溢的结点V,插入之前满足条件(关键字个数小于等于 m), 插入之后大于m, 因此 V结点现在恰好有 m+1 个关键字。 将该关键字分裂操作: 取V结点中间的关键字 $K_s(s=(m+l)/2)$ , 将$K_s$上升到其父结点 P, 左右两部分作为$K_s$的左右孩子,如图 10-61 所示。
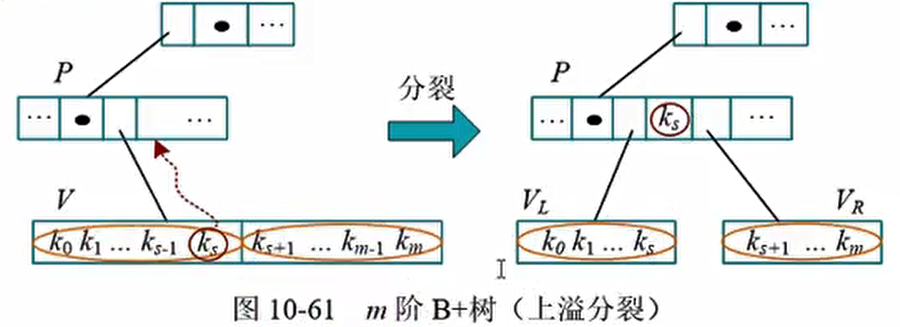
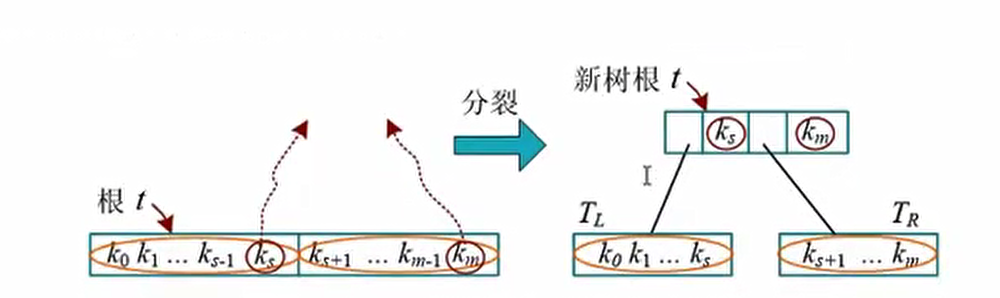
中间关键字上升到父结点后,需要检杳父结点是否发生上溢,如果发生上溢, 则继续分裂, 一直向上传递, 最远到达树根。 如果根结点发生上溢,则要以下特殊处理:
树根分裂操作而要分裂的两个于结点的最大关键字一起上升,生成 个新的结点作为新树根, 此时树高增1。 如下所示。
未发生上溢

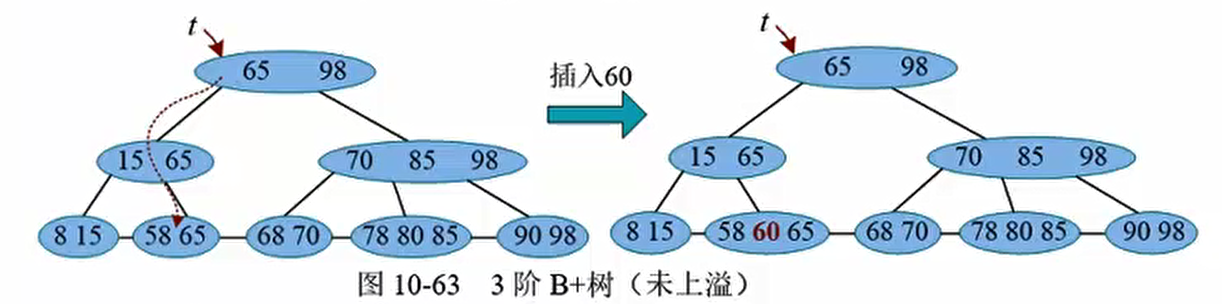
发生上溢
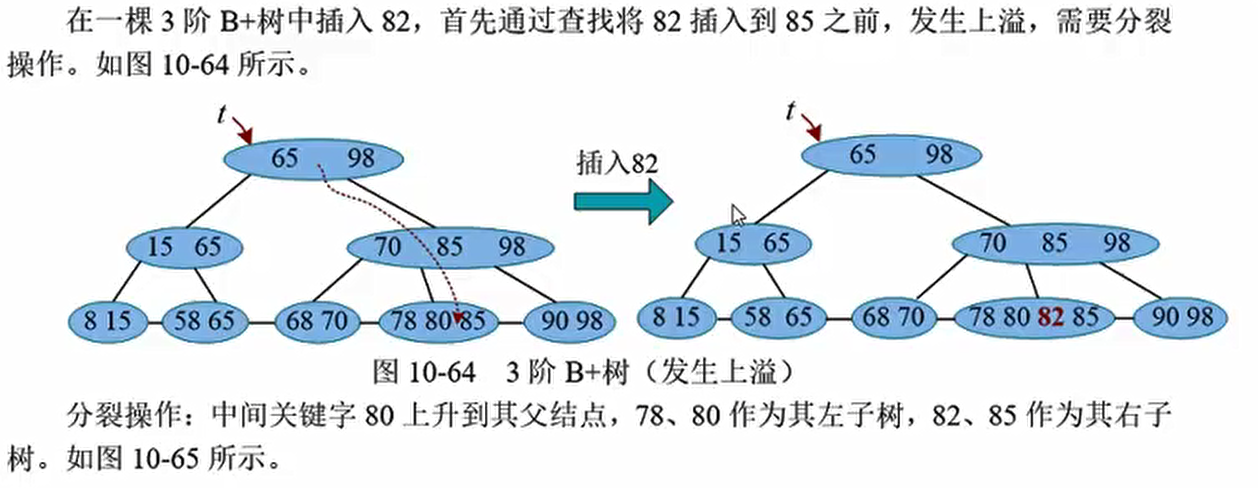
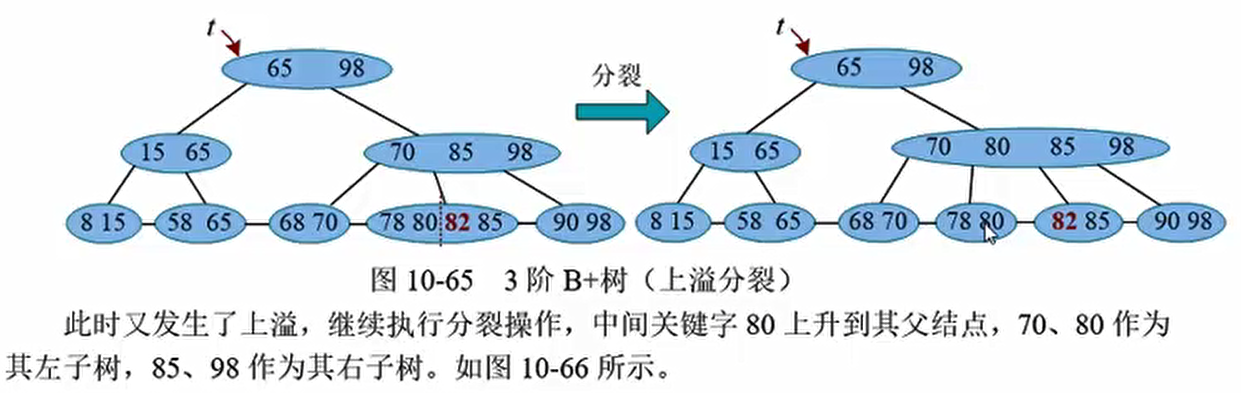
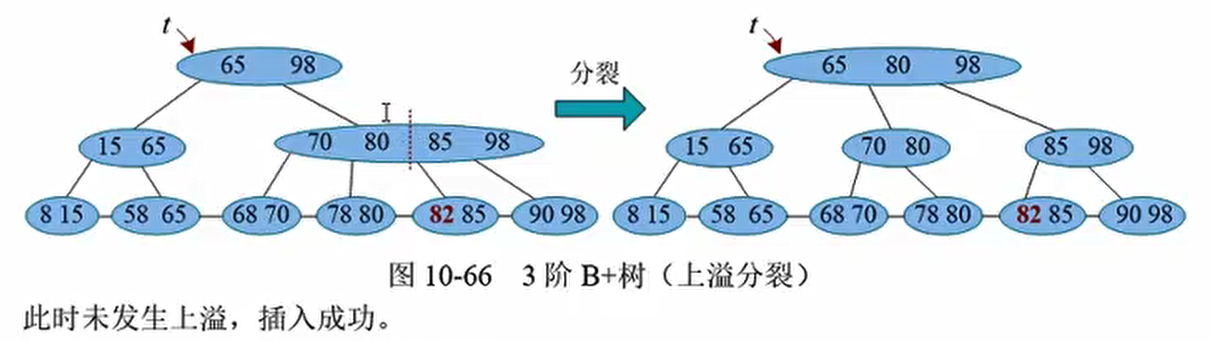
特殊情况(树根分裂)
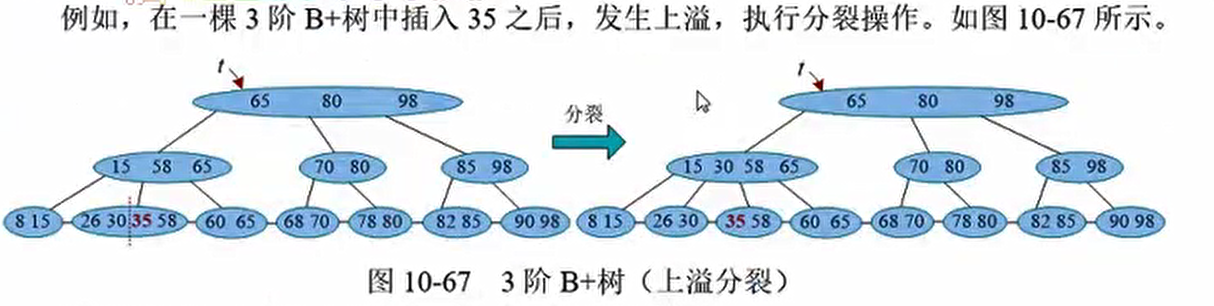
练习:
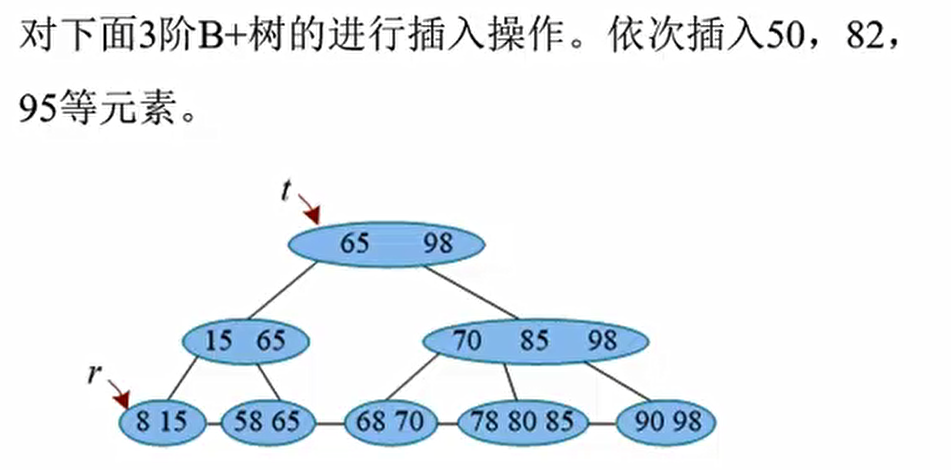
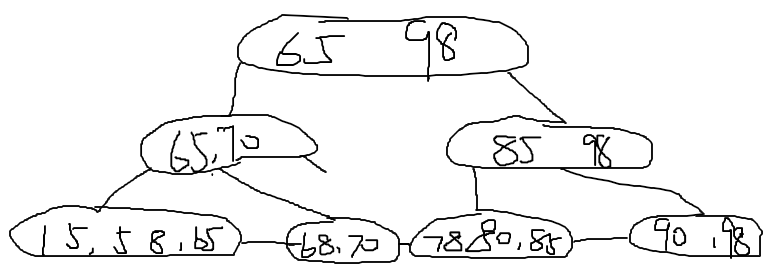
50 插入,不分裂
82插入,分裂,第二层变为70,80,85,98,再次发生分裂。树根变为 65 80 98
- 95插入,不分裂
记住,如果插入的关键字比较大,一定要更新一个索引
B+树的删除
m阶B+树的删除只在最后一层进行,首先通过查找确定待删除关键字的位置,删除之,然后判断该结点是否发生下溢,还要判断是否需要更新父结点的关键字。如果关键字个数小于 $\lceil m/2\rceil$ 时发生下溢。如果发生下溢则需要像B- 树那样左借、右借或合并操作解除下溢。解除下溢时要特别注意父结点中的最大关键字更新。
未发生下溢
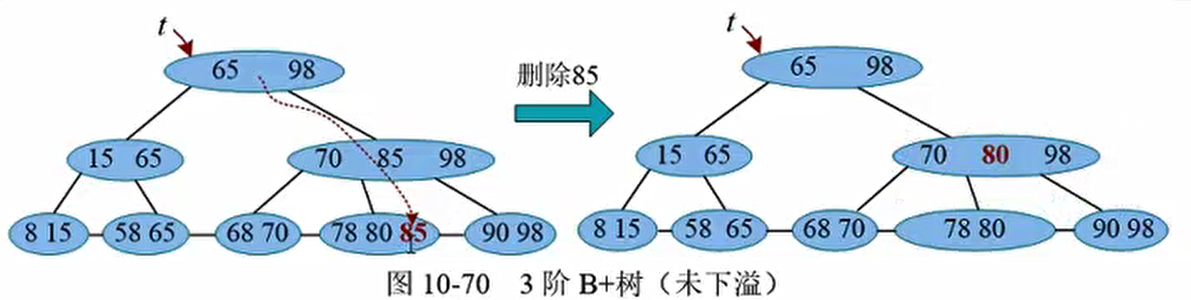
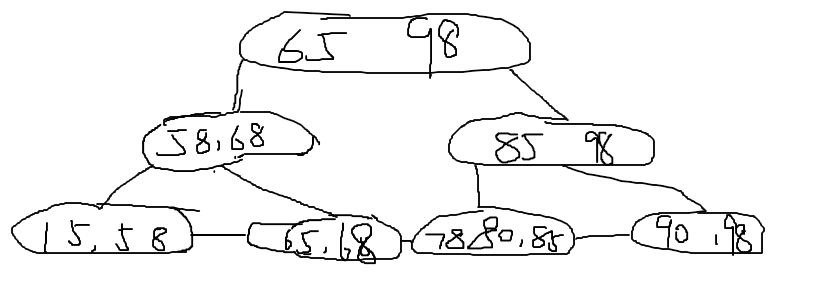
在一棵3阶B+树中删除85,首先查找到85的位置,删除之。删除后未发生下溢,但是该孩子节点的最大关键字为80,需要更新其父结点中该位置关键字为80.
发生下溢(右借或左借)
在一棵3阶B+树中删除68,首先查找到68的位置,删除之。删除后该节点关键字个数小于2,因此发生下溢,左兄弟只有2个关键字不可以借,右兄弟有3 个关键字,向右兄弟可以借一个,然后更新父节点
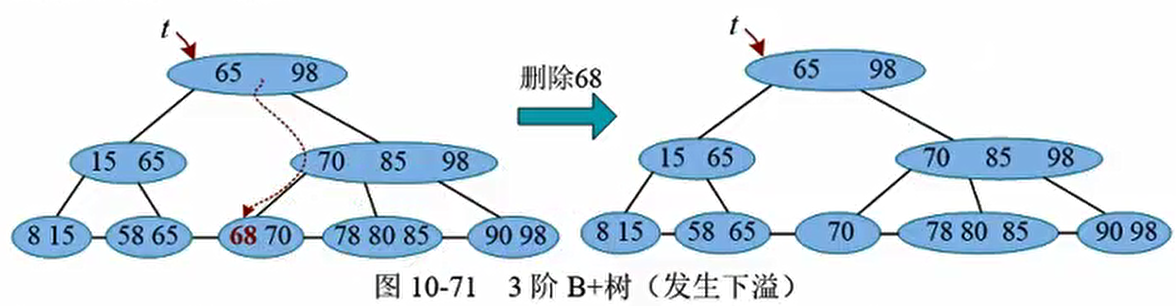
可以向右兄弟借一个关键字78.借后更新父节点该位置最大的关键字为78.如图
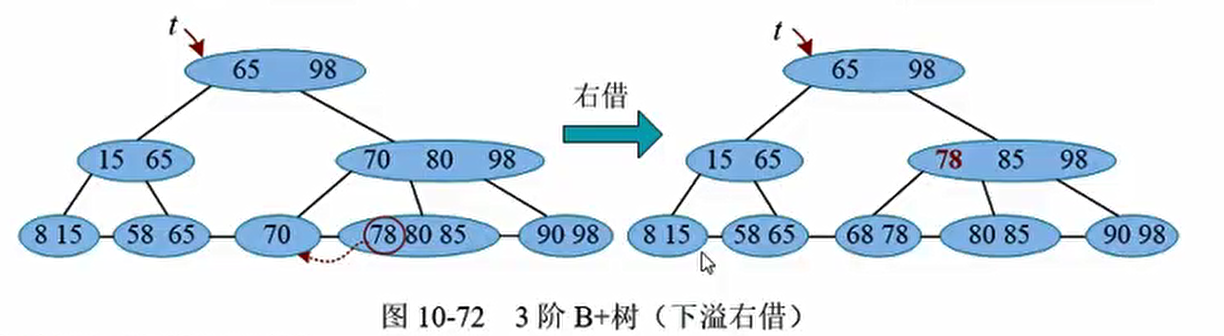
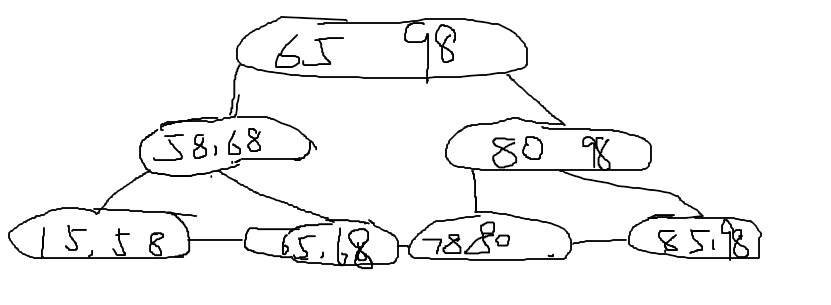
发生下溢(合并)
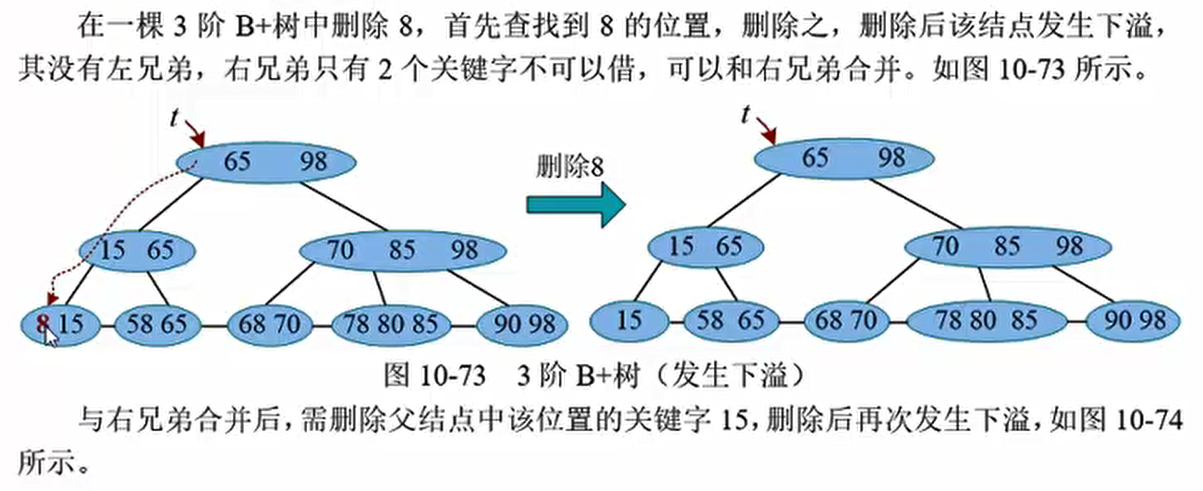
发生下溢(树根)
练习
算法分析
含有 n个关键字的m阶B+树,查找、插入和删除操作的时间复杂度均为树的高度$O(\log_mn)$