拓扑排序

​ —个无环的有向图称为有向无环图 (DirectedAcycline Graph, DAG)。$11$

​ 有向无环图是描述—个工程、 计划、 生产、 系统等流程的有效工具。 —个大工程可分为若干个子工程（活动）， 活动之间通常有—定的约束， 例如先做什么活动， 什么活动完成后才可以开始下—个活动。

​ 用顶点表示活动， 用弧表示活动之间的优先关系的有向图， 称为顶点表示活动的网 (Activity On Vertex Network), 简称 AOV 网。

​ 在 AOV 网中，若从顶点i 到顶点之间存在—条有向路径， 称顶点 i 是顶点 j 的前驱， 或者称顶点 j 是顶点 i 的后继。 若是图中的弧， 则称顶点i是顶点j 的互接前驱， 顶点 j 是顶点 i 的互接后驱。

​ AOV网中的弧表示了活动之间存在的制约关系。 例如， 计算机专业的学生必须完成一系列规定的基础课和专业课才能毕业．学生按照怎样的顺序来学习这些课程呢？这个问题可以被看成是一个大的工程， 其活动就是学习每一门课程。这些课程的名称和代号如下表所示

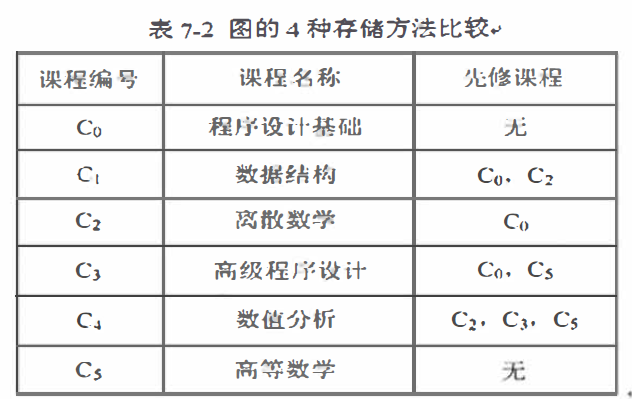
如果用顶点表示课程，弧表示先修关系，若课程i是课程j的先修课程，在用弧 表示，课程之间的关系如图

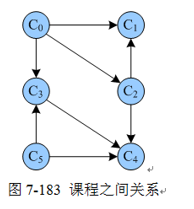
要想找什么课程先修，那就看有没有入度。入度为0即可输出。比如这里C0,C5都是可以先输出的

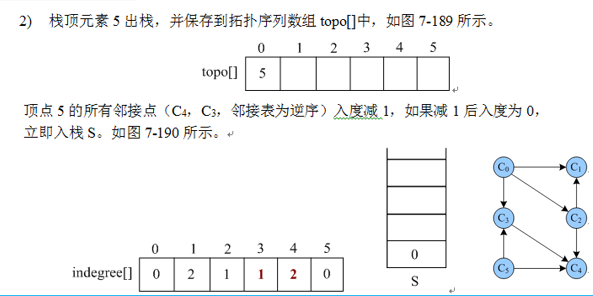
C0一旦输出以后，C0的出度全部去掉。所以C1的入度从2变成了1……

AOV网中是不允许有环的，否则会出现自己是自己的前驱，陷入死循环。怎么判断AOV网中， 是否有环呢？一个检测的办法是对有向图的顶点进行拓扑排序。如果AOV网中所有的顶点都在拓扑序列中， 则AOV网中必定无环。因为有环的话，这个环中的每个顶点都是存在入度的

拓扑排序是指将AOV网中的顶点排成一个线性序列，该序列必须满足： 若从顶点i到j有一条路径， 则该序列中顶点i一定在顶点j 之前

如果进行拓扑排序呢?

基本思想

1) 选择—个无前驱的顶点并输出

2) 从图中删除该顶点和该顶点的所有发出边

3) 重复 1) 和 2), 直到不存在无前驱的顶点。

4) 如果输出的顶点数小于AOV网中的顶点数， 则说明网中有环，否则输出的序列即为拓扑序列。

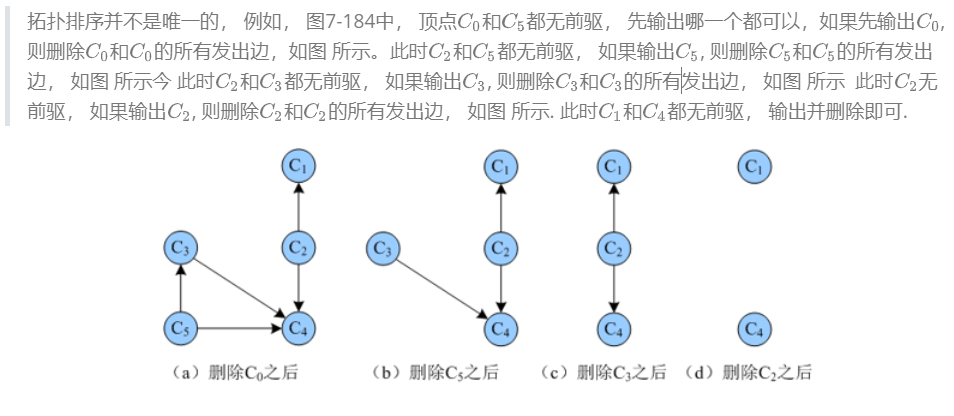
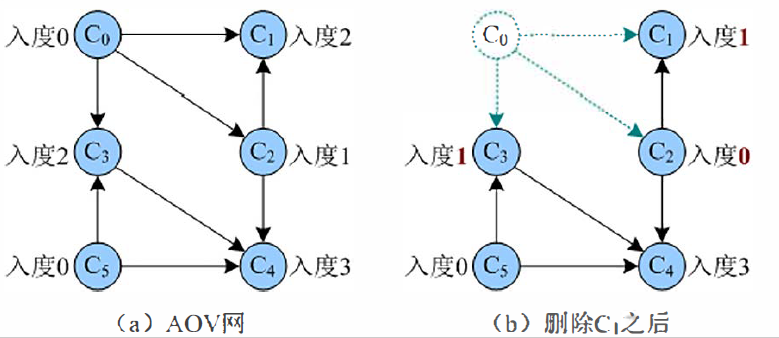
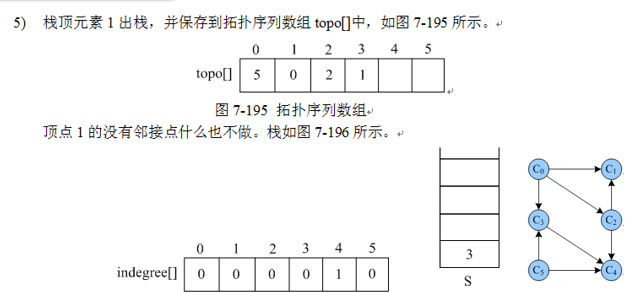
上述的描述过程中，有删除顶点和边的操作，实际上， 完全没必要真的删除顶点和边 。 可以将没有前驱的顶点 （入度为0) 暂存到栈中，输出时出栈即表示删除 。边的删除只需要将其邻接点的入度减一即可。 例如图中， 删除C0的所有发出边， 相当于将 C3, C2, C1 顶点的入度减去1, 如图 7-185 所示。

算法

1) 求出各顶点的入度, 存入数组 indegree[]中，并将入度为0 的顶点入栈S。.,
2) 如果栈不空， 则重复执行以下操作

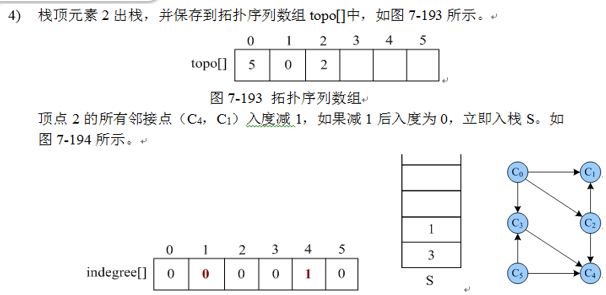
• 栈顶元素i出栈，并保存到拓扑序列数组 topo[]中
• 顶点i 的所有邻接点入度减1, 如果减1后入度为 0 , 立即入栈S.

3) 如果输出的顶点数小千 AOV网中的顶点数，则说明网中有环，否则输出拓扑序列。

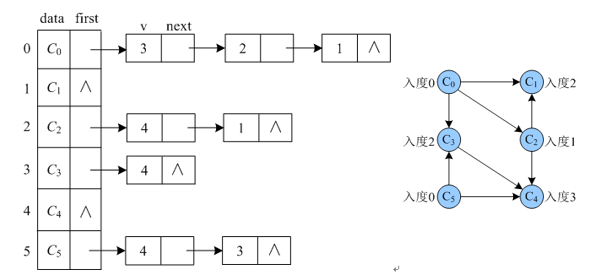
因为经常要访问临界点，所以邻接表和链式前向星(静态邻接表)更好。 邻接表访问邻接点容易，计算入度难，因此为了计算顶点的入度，在创建邻接表的同时，再创建一个逆邻接表，根据逆邻接表计算各顶点的入度。

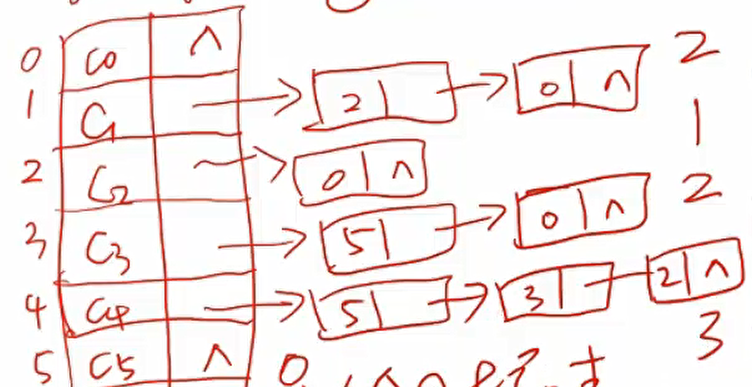
步骤

算法分析

时间复杂度：求有向图中各顶点的入度需要遍历逆邻接表，算法的时间复杂度为O(e)。 度数为0的顶点入栈的时间复杂度为O(n), 若有向图无环，每个顶点出栈后其邻接点入度减1, 时间复杂度为O(e)。 总的时间复杂度为O(n+e)。

空间复杂度：算法所需要的辅助空间包含入度数组indegree[]、拓扑序列数组 topo[] 、栈s, 则算法的空间复杂度是O(n)

算法可视化 https://visualgo.net/zh/dfsbfs

https://www.cs.usfca.edu/~galles/visualization/TopoSortIndegree.html

代码一览

#include<iostream>
#include<cstring>
#include<stack>
using namespace std;
const int MaxVnum=100;//顶点数最大值
int indegree[MaxVnum];//入度数组

typedef string VexType;//顶点的数据类型为字符串型
typedef struct AdjNode{ //定义邻接点类型
	int v; //邻接点下标
	struct AdjNode *next; //指向下一个邻接点
}AdjNode;

typedef struct VexNode{ //定义顶点类型
	VexType data; // VexType为顶点的数据类型，根据需要定义
	AdjNode *first; //指向第一个邻接点
}VexNode;

typedef struct{//包含邻接表和逆邻接表
    VexNode Vex[MaxVnum]; //定义邻接表
    VexNode converse_Vex[MaxVnum]; //定义逆邻接表
    int vexnum,edgenum; //顶点数，边数
}ALGragh;

int locatevex(ALGragh G,VexType x)
{
    for(int i=0;i<G.vexnum;i++)//查找顶点信息的下标
       if(x==G.Vex[i].data)
        return i;
    return -1;//没找到
}

void insertedge(ALGragh &G,int i,int j)//插入一条边
{
    AdjNode *s1,*s2;
    s1=new AdjNode;//创建邻接表结点
    s1->v=j;
    s1->next=G.Vex[i].first;
    G.Vex[i].first=s1;
    s2=new AdjNode;//创建逆邻接表结点
    s2->v=i;
    s2->next=G.converse_Vex[j].first;
    G.converse_Vex[j].first=s2;
}

void printg(ALGragh G)//输出邻接表
{
   cout<<"----------邻接表如下：----------"<<endl;
   for(int i=0;i<G.vexnum;i++)
   {
       AdjNode *t=G.Vex[i].first;
       cout<<G.Vex[i].data<<"：  ";
       while(t!=NULL)
       {
           cout<<"["<<t->v<<"]  ";
           t=t->next;
       }
       cout<<endl;
   }
   cout<<"----------逆邻接表如下：----------"<<endl;
   for(int i=0;i<G.vexnum;i++)
   {
       AdjNode *t=G.converse_Vex[i].first;
       cout<<G.converse_Vex[i].data<<"：  ";
       while(t!=NULL)
       {
           cout<<"["<<t->v<<"]  ";
           t=t->next;
       }
       cout<<endl;
   }
}

void CreateALGraph(ALGragh &G)//创建有向图的邻接表和逆邻接表
{
    int i,j;
    VexType u,v;
    cout<<"请输入顶点数和边数:"<<endl;
    cin>>G.vexnum>>G.edgenum;
    cout << "请输入顶点信息:"<<endl;
    for(i=0;i<G.vexnum;i++)//输入顶点信息，存入顶点信息数组
    {
        cin>>G.Vex[i].data;
        G.converse_Vex[i].data=G.Vex[i].data;
        G.Vex[i].first=NULL;
        G.converse_Vex[i].first=NULL;
    }
    cout<<"请依次输入每条边的两个顶点u,v"<<endl;
    while(G.edgenum--)
    {
        cin>>u>>v;
        i=locatevex(G,u);//查找顶点u的存储下标
        j=locatevex(G,v);//查找顶点v的存储下标
        if(i!=-1&&j!=-1)
            insertedge(G,i,j);
        else
        {
           cout << "输入顶点信息错！请重新输入！"<<endl;
           G.edgenum++;//本次输入不算
        }
    }
}

void FindInDegree(ALGragh G)//求出各顶点的入度存入数组indegree中
{
	int i,count;
	for(i=0;i<G.vexnum; i++)
    {
        count=0;
        AdjNode *p=G.converse_Vex[i].first;
		if(p)
		{
			while(p)
			{
				p=p->next;
				count++;
			}
		}
		indegree[i]=count;
	}
	cout<<"入度数组为："<<endl;
	for(int i=0;i<G.vexnum;i++)//输出入度数组
       cout<<indegree[i]<<"\t";
    cout<<endl;
}

bool TopologicalSort(ALGragh G, int topo[])//拓扑排序
{
    //有向图G采用邻接表存储结构
    //若G无回路，则生成G的一个拓扑序列topo[]并返回true，否则false
	int i,m;
	stack<int>S;      //初始化一个栈S，需要引入头文件#include<stack>
    FindInDegree(G);  //求出各顶点的入度存入数组indegree[]中
    for(i=0;i<G.vexnum;i++)
		if(!indegree[i])//入度为0者进栈
            S.push(i);
	m=0;            //对输出顶点计数，初始为0
	while(!S.empty())//栈S非空
    {
		i=S.top();    //取栈顶顶点i
        S.pop();      //栈顶顶点i出栈
		topo[m]=i;    //将i保存在拓扑序列数组topo中
		m++;          //对输出顶点计数
		AdjNode *p=G.Vex[i].first;  //p指向i的第一个邻接点
		while(p) //i的所有邻接点入度减1
        {
			int k=p->v;			 //k为i的邻接点
			--indegree[k];       //i的每个邻接点的入度减1
			if(indegree[k]==0)  //若入度减为0，则入栈
			  S.push(k);
			p=p->next;      //p指向顶点i下一个邻接结点
		}
	}
	if(m<G.vexnum)//该有向图有回路
        return false;
	else
		return true;
}

int main()
{
    ALGragh G;
    int *topo=new int[G.vexnum];
    CreateALGraph(G);//创建有向图的邻接表和逆邻接表
    printg(G);//输出邻接表和逆邻接表
    if(TopologicalSort(G,topo))
    {
        cout<<"拓扑序列为："<<endl;
        for(int i=0;i<G.vexnum;i++)//输出拓扑序列
            cout<<topo[i]<<"\t";
    }
    else
        cout<<"该图有环，无拓扑序列！"<<endl;
    return 0;
}

第二种算法

假设这是有向无环图。

#include<iostream>
#include<cstring>
#include<stack>
using namespace std;
const int maxn=105;
int map[maxn][maxn],indegree[maxn],topo[maxn];//利用了邻接矩阵
int n,m;
stack<int>s;
//不接受字符串，只能整数
void TopoSort() //拓扑排序
{
	int cnt=0;
    for(int i=1;i<=n;i++) //入度为0的全部都入栈
        if(indegree[i]==0)
        	s.push(i);
    while(!s.empty())
    {
		int u=s.top(); //取栈顶
    	s.pop();	   //出栈
    	topo[++cnt]=u; //然后把u存储到topo数组当中
    	for(int j=1;j<=n;j++)//访问所有u的邻接点
            if(map[u][j])
            	if(--indegree[j]==0)//然后把临界点的入度减一
        			s.push(j);	
	}
}

int main()
{
    cin>>n>>m;//节点数和边数
    memset(map,0,sizeof(map));
    memset(indegree,0,sizeof(indegree));
	for(int i=1;i<=m;i++)
    {
    	int u,v;
    	while(cin>>u>>v)//输入边
    	{
    		map[u][v]=1;//表示有一条u->v的边
    		indegree[v]++;//立即入度++
		}
	}
	TopoSort();
	for(int i=1;i<n;i++)
		cout<<topo[i]<<" ";
	cout<<topo[n]<<endl;
    return 0;
}