离散数学之图3
Euler Paths and Circuits
Definition
定义:An Euler circuit in a graph G is a simple circuit containing every edge of G. An Euler path in G is a simple path containing every edge of G
欧拉环的定义就是一个简单环,边不能重复,且最后需要回到起点。 欧拉路径就是不要求一定回到起点,但是要求走过每一条边且不能重复
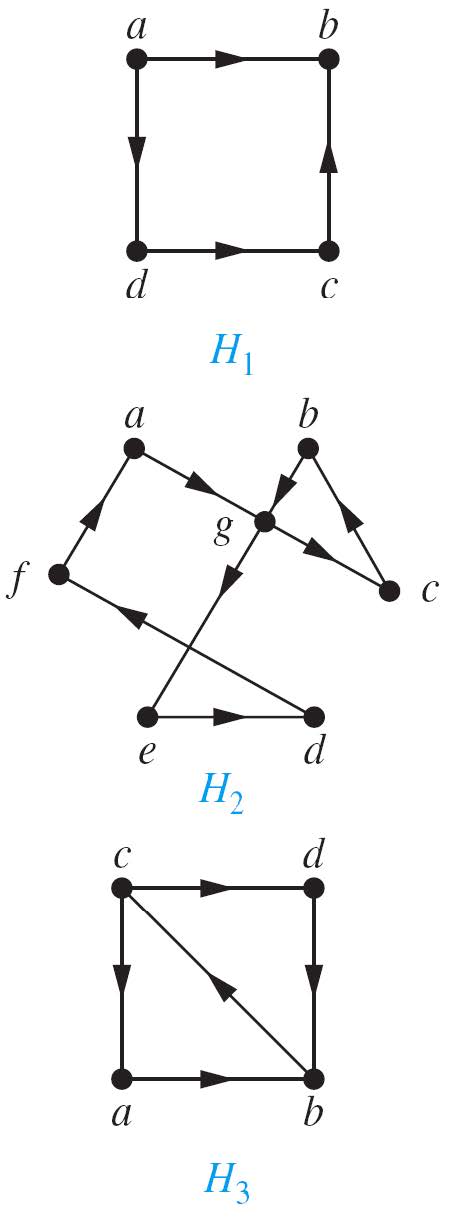
向上面三幅图,H1既不是欧拉环也不是欧拉路径;H2有一个欧拉环;H3有一条欧拉路径
对于一副图来说,我们如何判断其有没有欧拉环或者欧拉路径呢?
对于欧拉环: 每一个节点的度必然是偶数。因为每一个点都有几进几出。如果发现了一个度为奇数的节点,那么这张图必然不可能是欧拉环
对于欧拉路径: 中间节点的度必须是偶数,但是起点和终点的度可以是奇数。如果是起点,出度比入度多1;如果是终点,入度比出度多1
戈尼斯堡七桥问题,就是一个典型的一笔画问题。
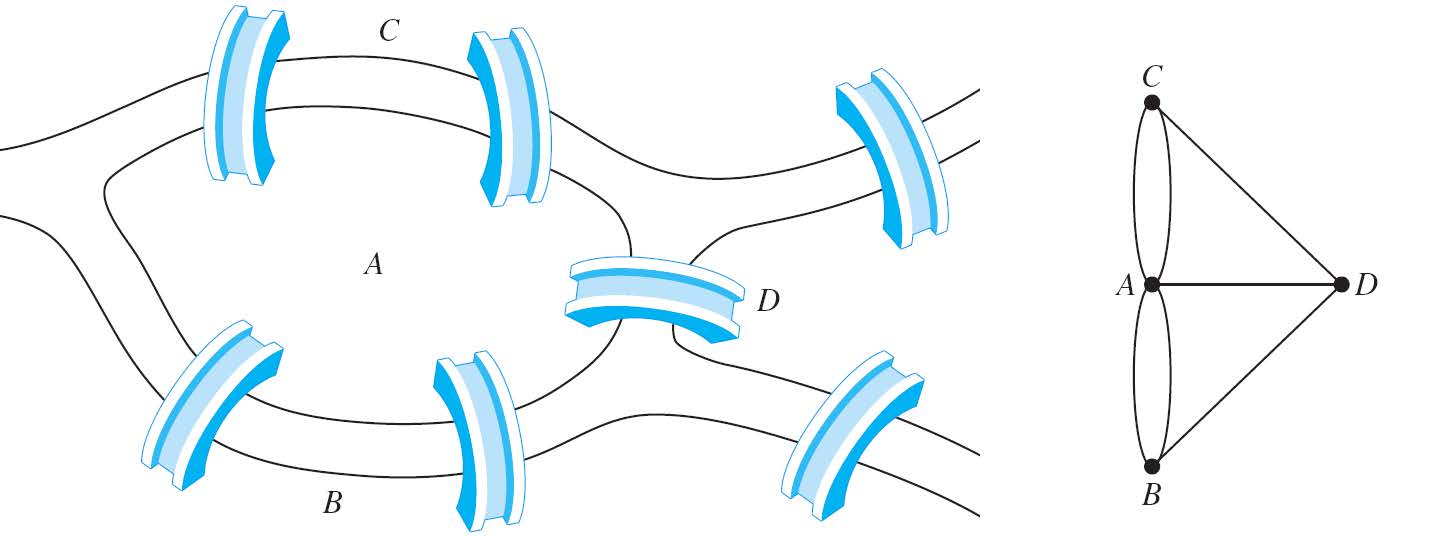
对于抽象出来的图,所有顶点(4个顶点)的度都是奇数。所以必然不存在欧拉环或欧拉路径。
对于无向图,如果度数为奇数的顶点为0个,那么可能存在欧拉环;如果是2个,那么可能存在欧拉路径;如果为4,6…那么必然不存在欧拉环或者欧拉路径
Necessary and sufficient for Euler circuit
A connected multigraph with at least two vertices has an Euler circuit if and only if each of its vertices has even degree.

Necessary and sufficient for Euler path
A connected multigraph has an Euler path but not an Euler circuit if and only if it has exactly two vertices of odd degree.
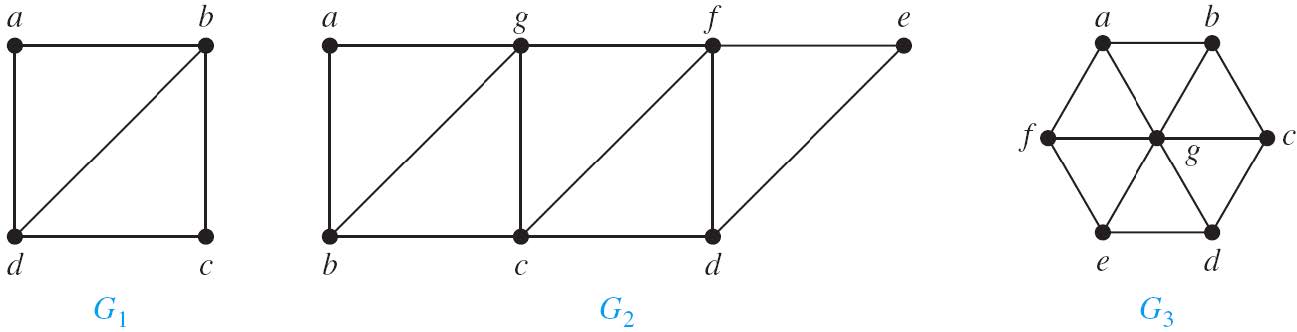
比如G1,有两个奇数度的顶点,可以有欧拉路径;G2,有两个奇数度的顶点,可以有欧拉路径,G3,有六个奇数度顶点的路径,所以不存在欧拉环或者欧拉路径
Hamilton Paths and Circuits
Definition
A simple path in a graph G that passes through every vertex exactly once is called a Hamilton path, and a simple circuit in a graph G that passes through every vertex exactly once is called a Hamilton circuit.
汉密尔顿路径和汉密尔顿环只要求顶点全部走过,边不一定要全部都走
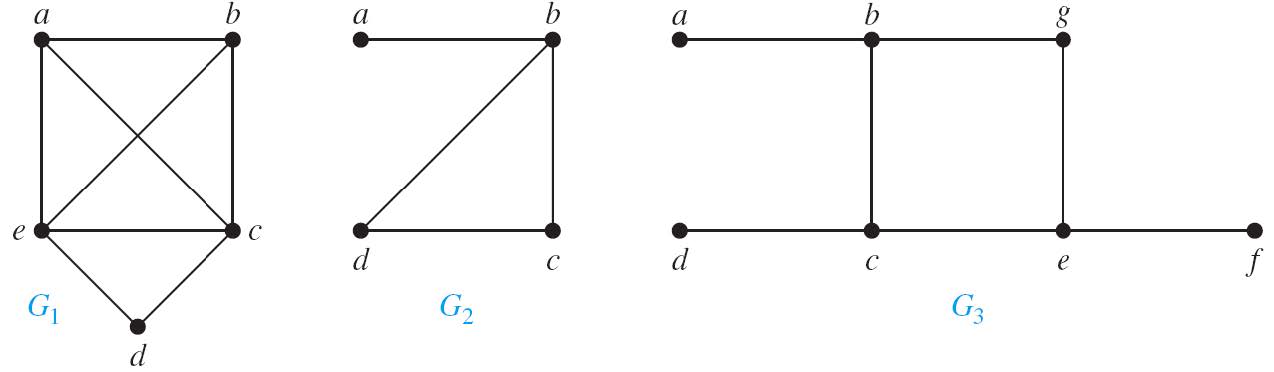
哈密尔顿环:每一个顶点的度至少为2.
哈密尔顿路径:所以如果度为1的顶点超过两个,那么这个图必然不可能存在哈密尔顿路径。小于等于2会存在哈密尔顿路径
Conditions for the existence
如果一个简单图的节点大于等于3,且每个节点的度至少是n/2.那么G就存在一个哈密尔顿环。
如果一个简单图的节点大于等于3,而且从中任意选择两个节点u和v,如果$deg(u)+deg(v)\geq n$ 成立,那么G中就存在一个哈密尔顿环
但是这并不能绝对说明没有哈密尔顿环存在,只能说了满足条件的一定存在。所以当一个图不满足狄拉克-奥勒定理的时候,我们还需要手动画一画

Planar Graphs 平面图
Definition
A graph is called planar if it can be drawn in the plane without any edges crossing (where a crossing of edges is the intersection of the lines or arcs representing them at a point other than their common endpoint).
平面图就是边和边没有交叉的图,我们可以对一些图进行变换,不改变图的结构来把原来交叉的图变成平面图

如何来判断一个图是否为平面图呢?
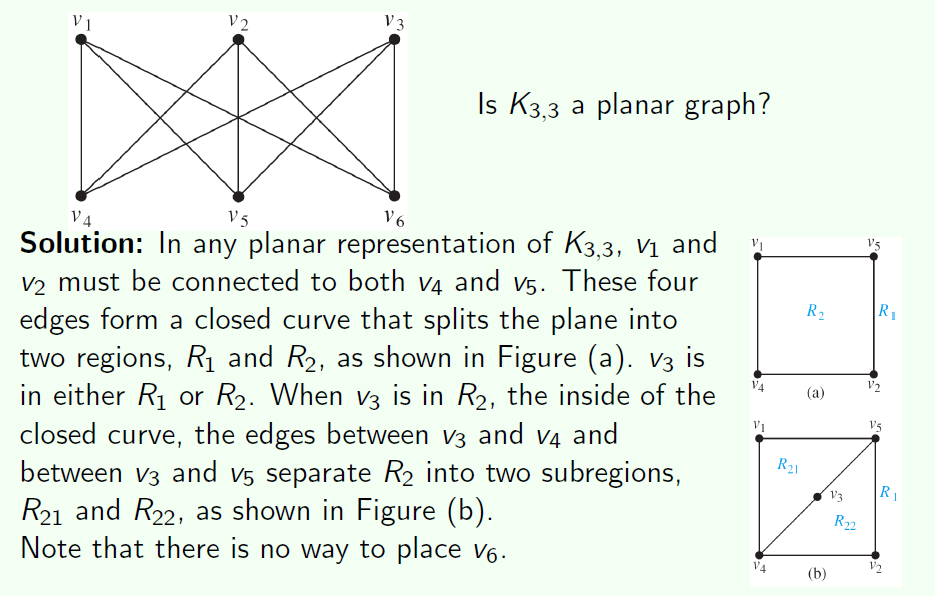
首先我们把四个点拿过来。$v1,v_2,v_4,v_5$ 这四个点构成了一个平面图。现在我们把$v_3$加进来,$v_3$需要和$v_4,v_5$相连。这时候我们把$v_6$放进来,$v_6$ 只能放在 $R_1,R{21},R_{22}$这三个区域当中
如果在 $R_1$当中,我要把$v_6,v_3$相连那么必然线与线要相交。以此类推,$v_6$ 无论在哪个区域,必然不可能是平面图。以此类推, K33这个二分图和以K33为子图的图必然不可能是平面图
所以我们要利用红黑点来画出二分图,再看看二分图中是否包含K3,3或者K5,以及和他们同胚的图(两个点之间可以通过第三个点连接).
Euler’s Formula
定理及证明
Let G be a connected planar simple graph with e edges and v vertices. Let r be the number of regions in a planar representation of G. Then $r = e - v + 2$.
r理解成面数,比如 长方体 ,6个面8个顶点12条棱,r=6,v=8,e=12;再如 正四面体,4个面4个顶点6条棱,r=4,v=4,e=6
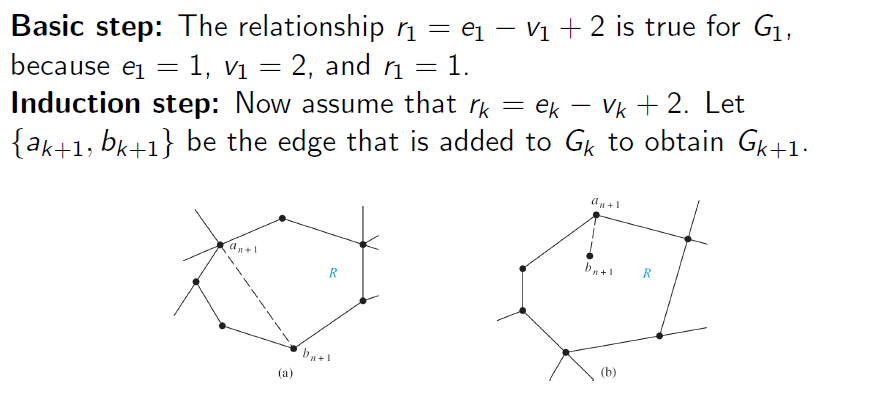

推论I

推论II

推论III

Homeomorphic 同胚
If a graph is planar, so will be any graph obtained by removing an edge ${u,v}$ and adding a new vertex w together with edges${u,w}$ and ${w,v}$. Such an operation is called an elementary subdivision. The graphs$ G1 = (V_1,E_1) $ and $ G2 = (V_2, E_2)$ are called homeomorphic if they can be obtained from the same graph by a sequence of elementary subdivisions.
加上了几个顶点或者减去几个顶点,把两幅图变成一幅图,那么这两幅图就是同胚的。
加或减顶点不会影响图的结构

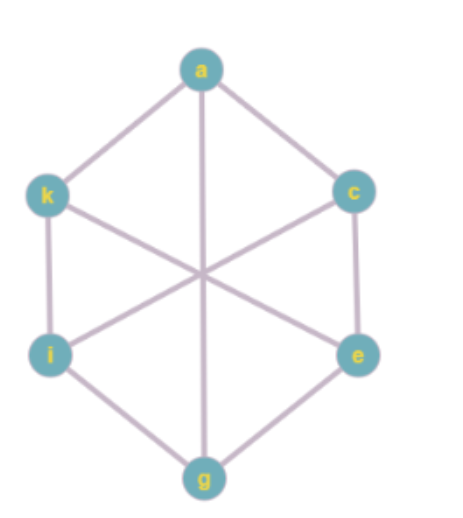
有一种让你看某张图是否为K3,3同胚的题形。要注意K3,3 可以是千变万化的。下面这个样子的图型也是K3,3!
K5 就类似于五角星勋章
还有一个判断的就是根据度来判断,K5的所有顶点的度至少为4,$K_{33}$的所有顶点的度至少为3
注意,同胚并不是说两个点之间有path即可
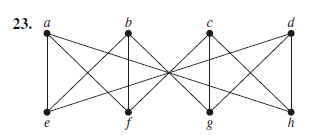
这个图并不是和K3,3 同胚的!
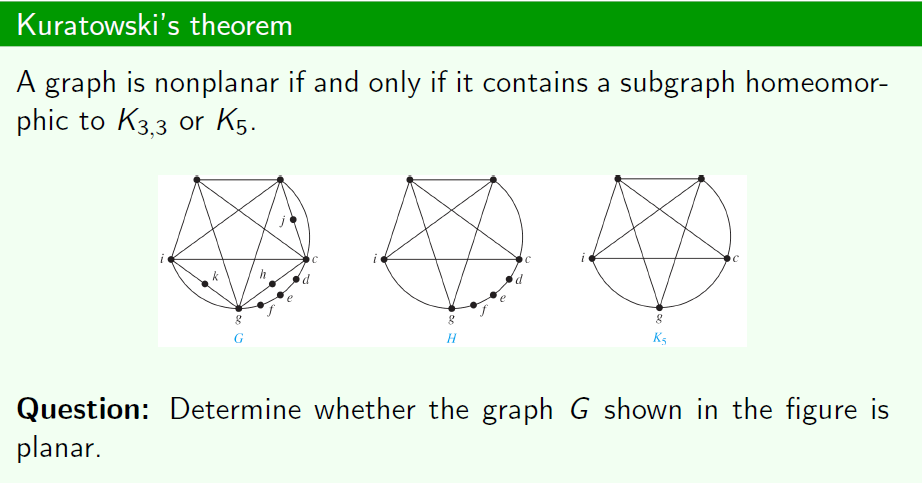
Kuratowski’s theorem
一个图如果不是平面图,当且仅当它有一个子图是和K5或者K33同胚的
Graph Coloring
Problem formulation
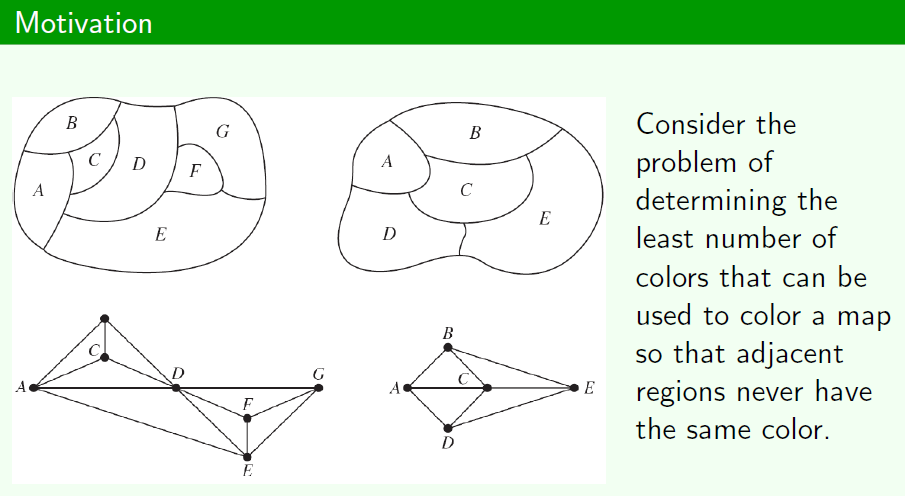
De nitions

The four color theorem
如果这个图是平面图,那么最小着色的色数不会超过4
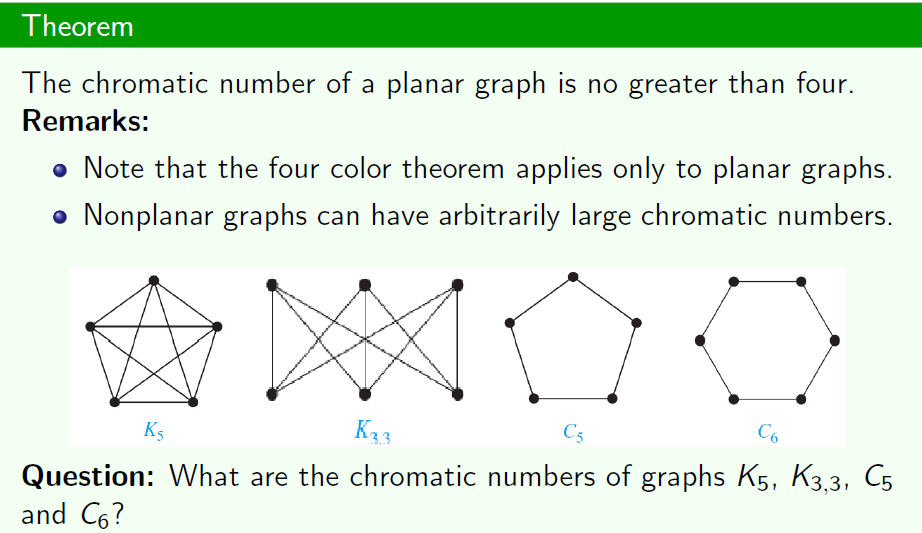
K5的话,最小着色为5,C5只要3个颜色,C6只要2个颜色