numpy基础

Posted on
Words count in article: 3.2k | Reading time ≈ 15

numpy基础

教程: https://www.youtube.com/watch?v=QUT1VHiLmmI

numpy documentation: https://numpy.org/doc/stable/numpy-user.pdf

What is NumPy

NumPy（Numerical Python）是Python的一种开源的数值计算扩展。这种工具可用来存储和处理大型矩阵，比Python自身的嵌套列表（nested list structure)结构要高效的多（该结构也可以用来表示矩阵（matrix）），支持大量的维度数组与矩阵运算，此外也针对数组运算提供大量的数学函数库

NumPy vs Lists (speed, functionality)

Numpy 和 python的Lists比起来要快得多

为什么 Numpy更快呢？

  1. numpy的许多函数不仅是用C和Fortran实现了，还使用了BLAS（一般Windows下link到MKL的，Linux下link到OpenBLAS）。基本上那些BLAS实现在每种操作上都进行了高度优化.
  2. 而且，我们在把一个数字转换成Numpy 和Lists的时候，Numpy只要转换成4bytes，但是转换成list却要生成：Size,Reference Count,Object Type 和Object Value，所以相比起来list占用了更多的空间，numpy读取更少的内存
  3. 在Numpy中，遍历时没有对数据的类型检查
  4. 在 Numpy中使用连续的内存来存储，但是lists中存储的数据是离散的，以哈希表的方式存储 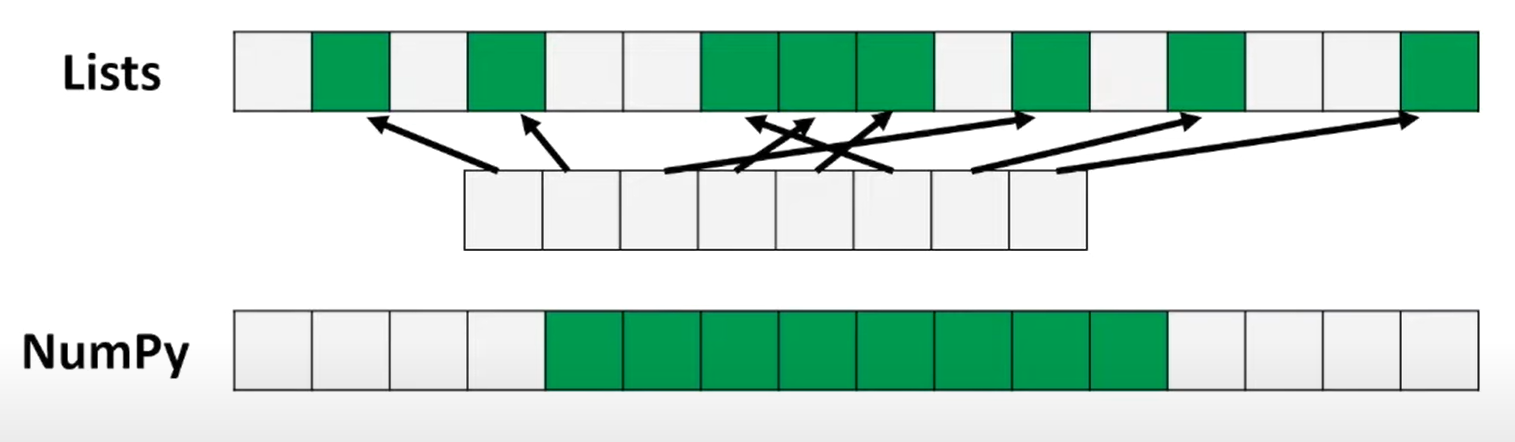这样做的好处是：1.SIMD vector Processing (向量编程)2.Effective Cache Utilization(有效的缓存利用率)

Differences Between Lists and Numpy

Lists Numpy
Insertion Insertion
deletion deletion
appending appending
concatenation concatenation
… Lots More than Lists!!!

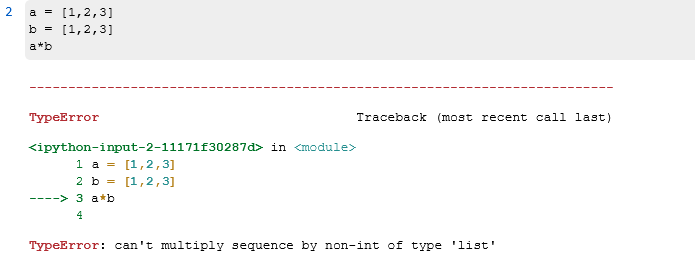
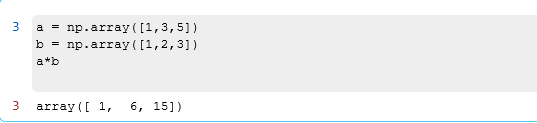
比如，我们可以对numpy的两个数组进行乘法，但是对两个list进行乘法就会报错：

Applications of NumPy

  • 我们可以对Numpy进行数学上的操作，用来当作Matlab的替代
  • 我们可以和Matplotlib进行画图操作
  • 用作 Pandas ，Connect 4 这些库的核心
  • 机器学习(神经网络)

The Basics (creating arrays, shape, size, data type)

creating arrays

1
2
a = np.array([1,2,3], dtype='int32')
print(a)
[1 2 3]

1
2
b = np.array([[9.0,8.0,7.0],[6.0,5.0,4.0]])
print(b)
[[9. 8. 7.]
[6. 5. 4.]]

Get Dimension

用 ndim 获取 numpy array 的维度

1
2
a.ndim
1
1
2
b.ndim
2

Get Shape

用 shape 获取当前数组的大小：b是 2x3，2行3列 是二维数组 。a是 (3,) 是一维数组

1
2
b.shape
(2, 3)
1
2
a.shape
(3,)

Get Type

用 dtype 来获取数组中的数据类型

1
2
a.dtype
dtype('int32')
1
2
b.dtype
dtype('float64')

Get size

itemsize获取数组中每一个元素占了几个字节

1
2
a.itemsize
4
1
2
b.itemsize
8

Get total size

nbytes 获取整个数组占用的字节

1
2
a.nbytes
12
1
2
b.nbytes
48

Get number of elements

size获取数组当中的元素个数

1
2
a.size
3
b.size
6

Accessing/Changing Specific Elements, Rows, Columns, etc (slicing)

1
2
a = np.array([[1,2,3,4,5,6,7],[8,9,10,11,12,13,14]])
print(a)
1
2
[[ 1  2  3  4  5  6  7]
 [ 8  9 10 11 12 13 14]]

Get a specific element [r, c]

我们可以用一个坐标定位一个目标元素

1
2
a[1, 5]
13

Get a specific row

用下面这种语法来获取目标行

1
2
a[0, :]
array([1, 2, 3, 4, 5, 6, 7])

Get a specific column

同样的我们可以获得目标列

1
2
a[:, 2]
array([ 3, 10])

Getting a little more fancy [startindex:endindex:stepsize]

第一个参数代表第一行，1：-1：2 代表起始点为a[1]，终点为a[6],步长为2 

1
2
a[0, 1:-1:2]
array([2, 4, 6])

把第二行第六列改成20

1
2
3
a[1,5] = 20
[[ 1  2  5  4  5  6  7]
 [ 8  9  5 11 12 20 14]]

把第三列改成 [1,2]

1
2
3
a[:,2] = [1,2]
[[ 1  2  1  4  5  6  7]
 [ 8  9  2 11 12 20 14]]

三维数组

我们嵌套两层数组，得到了三维数组

1
2
3
4
5
6
7
b = np.array([[[1,2],[3,4]],[[5,6],[7,8]]])
print(b)
[[[1 2]
  [3 4]]

 [[5 6]
  [7 8]]]
1
2
3
4
5
6
7
8
9
10
b = np.array([[[1,2],[3,4]],[[5,6],[7,8]],[[9,10],[10,11]]])
print(b)
[[[ 1  2]
  [ 3  4]]

 [[ 5  6]
  [ 7  8]]

 [[ 9 10]
  [10 11]]]

获得三维数组中的特定元素

1
2
b[0,1,1]
4

获取一个维度的元素

1
2
3
4
b[:,1,:]
array([[ 3,  4],
       [ 7,  8],
       [10, 11]])
1
2
b[:,0,0]
array([1, 5, 9])

替换一个维度的元素

1
2
3
4
5
6
7
8
9
10
b[:,1,:] = [[9,9],[8,8],[7,7]]
b
array([[[ 1,  2],
        [ 9,  9]],

       [[ 5,  6],
        [ 8,  8]],

       [[ 9, 10],
        [ 7,  7]]])

Initializing Different Arrays (1s, 0s, full, random, etc…)

All zeros matrix

创建一个全是0的矩阵，利用zeros()方法

1
2
3
np.zeros((2,3))
array([[0., 0., 0.],
       [0., 0., 0.]])
1
2
3
4
5
6
7
8
np.zeros((2,3,3))
array([[[0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.]],

       [[0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.]]])

All 1s matrix

创建全是1的矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
# 
np.ones((4,2,2), dtype='int32')
array([[[1, 1],
        [1, 1]],

       [[1, 1],
        [1, 1]],

       [[1, 1],
        [1, 1]],

       [[1, 1],
        [1, 1]]])

Any other number

创建全是指定数据的矩阵

1
2
3
np.full((2,2), 99)
array([[99., 99.],
       [99., 99.]], dtype=float32)

full_like 第一个参数是已经建立的一个数组，然后新建一个大小相同的数组把所有的数据都替换成第二个参数

np.full_like(a,4) = np.full(a.shape,4)

1
2
3
4
a = np.array([[1,2,3,4,5,6,7],[8,9,10,11,12,13,14]])
np.full_like(a, 4)
array([[4, 4, 4, 4, 4, 4, 4],
       [4, 4, 4, 4, 4, 4, 4]])

Random decimal numbers

random.rand

创建一个随机的数组 随机数取 0-1

1
2
3
4
5
np.random.rand(4,2)
array([[0.07805642, 0.53385716],
       [0.02494273, 0.99955252],
       [0.48588042, 0.91247437],
       [0.27779213, 0.16597751]])
random.random_sample

我们利用random_sample 方法，传入一个矩阵的shape，然后numpy会我们往这个shape中填充随机数

1
2
3
4
5
np.random.random_sample(a.shape)
array([[0.92880174, 0.99699795, 0.48302062, 0.30241305, 0.99854465,
        0.66126378, 0.46142038],
       [0.26466749, 0.89392165, 0.73333993, 0.75751601, 0.02252249,
        0.26214715, 0.9163327 ]])
np.random.randint

随机整数值，如果只有两个参数，那么就是0 - i-1中的随机数

1
2
3
4
np.random.randint(8, size=(3,3))
array([[2, 0, 7],
       [2, 4, 4],
       [0, 1, 6]])

如果有三个参数，前面两个参数是整数范围，第三个参数是矩阵大小

1
2
3
4
np.random.randint(-4,8, size=(3,3))
array([[-2, -4, -4],
       [ 6,  6,  3],
       [ 3,  2,  2]])
random.seed()

使随即数据可预测，对于同一个seed，生成的随机数相同

1
2
3
4
5
6
7
8
9
np.random.seed(0)
np.random.rand(1)
array([0.5488135])
np.random.seed(1)
np.random.rand(1)
array([0.4359949])
np.random.seed(1)
np.random.rand(1)
array([0.4359949])
random.randn()

生成指定维度的服从标准正态分布的随机数，输入参数为维度

1
np.random.randn(2,4) #返回一个shape为[2,4]的array，array中的元素服从标准正态分布
random.uniform()

方法将随机生成下一个实数，它在 [x, y] 范围内。第三个参数可选，是生成数据的数量

The identity matrix

创建一个标准矩阵，也就是我们说的 $E$ 或者 $I$

1
2
3
4
5
6
np.identity(5)
array([[1., 0., 0., 0., 0.],
       [0., 1., 0., 0., 0.],
       [0., 0., 1., 0., 0.],
       [0., 0., 0., 1., 0.],
       [0., 0., 0., 0., 1.]])

Repeat an array

重复一个数组

1
2
3
4
5
6
arr = np.array([[1,2,3]])
r1 = np.repeat(arr,3, axis=0)
print(r1)
[[1 2 3]
 [1 2 3]
 [1 2 3]]

Problem

怎么初始化一个这样的矩阵？？？

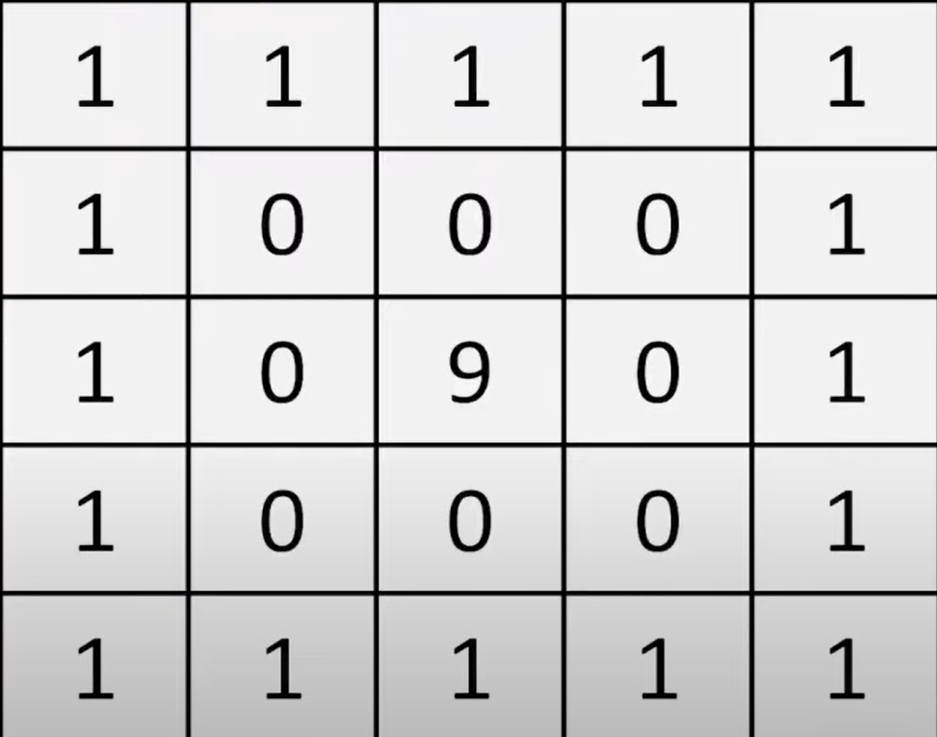
首先我们初始化一个 5x5 的全为1的矩阵output

其次我们初始化一个3x3全是0的矩阵z，并把z的中心元素改成9

最后我们把output矩阵中从output[1,1]到output-1,-1\ 这个 3x3 的子矩阵替换成z

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
output = np.ones((5,5))
print(output)
[[1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1.]]
z = np.zeros((3,3))
z[1,1] = 9
print(z)
[[0. 0. 0.]
 [0. 9. 0.]
 [0. 0. 0.]]
output[1:-1,1:-1] = z
print(output)
[[1. 1. 1. 1. 1.]
 [1. 0. 0. 0. 1.]
 [1. 0. 9. 0. 1.]
 [1. 0. 0. 0. 1.]
 [1. 1. 1. 1. 1.]]

框框中的数据的索引怎么有效的表示???

Be careful when copying arrays!!!

如果我们做一个浅拷贝，那么当修改了b之后，a也会随之改变，因为复制给b的是a的地址。

1
2
3
4
5
a = np.array([1,2,3])
b = a 
b[0] = 100
print(a)
[100 2 3]

所以我们需要用到copy()方法，这是一个深拷贝，也就是另外申请一段内存给b，然后把a中的值拷贝给b

1
2
3
4
5
a = np.array([1,2,3])
b = a.copy()
b[0] = 100
print(a)
[1 2 3]

Basic Mathematics (arithmetic, trigonometry, etc.)

Numpy中的行列维度，axis=0，1，2判断

1
2
3
4
5
6
7
8
9
10
11
12
13
A = np.array([1, 2, 3, 4, 5, 6])
print(A.sum(axis = 0))
>>>21

B = np.array([[1, 2], [3, 4], [5, 6]])
print(B.sum(axis = 0))
>>>[ 9 12]		# [1,2] + [3, 4] +[5, 6] = [9, 12]  每一行的和
print(B.sum(axis = 1))
>>>[ 3  7 11]		#[1, 3, 5] + [2, 4, 6] = [3, 7, 11] 每一列的和

C = np.array([[[1], [2]], [[3], [4]], [[5], [6]]])
print(C.sum(axis = 0))
>>>[[ 9] [12]]

axis是轴的意思，跟维度一样，是从0开始索引。
二维数组中有两个轴：

  1. 0轴沿着0行到1行的方向垂直向下（纵向）
  2. 1轴沿着0列到1列的方向水平延伸（横向）

由于行列没有方向的属性，所以这里用0行到1行的向量来表示方向加强记忆， 这样就又符合行列习惯了 （0对应行，1对应列）

更多方法见 Numpy的文档(https://docs.scipy.org/doc/numpy/reference/routines.math.html)

对一些数组进行操作:

1
2
3
a = np.array([1,2,3,4])
print(a)
[1 2 3 4]

a中所有的元素都加上2，以此类推

1
2
a + 2
array([5, 6, 7, 8])
1
2
a - 2
array([-1,  0,  1,  2])
1
2
a * 2
array([2, 4, 6, 8])
1
2
a / 2
array([0.5, 1. , 1.5, 2. ])

a+b 就是a和b数组中对应的元素相加

1
2
3
4
a = np.array([1,2,3,4])
b = np.array([1,0,1,0])
a + b
array([2, 2, 4, 4])

a中所有元素的平方

1
2
a ** 2
array([ 1,  4,  9, 16], dtype=int32)

显示a中所有元素的sin值/cos值

1
2
3
# Take the cos
np.cos(a)
array([ 0.54030231, -0.41614684, -0.9899925 , -0.65364362])
1
2
3
# Take the sin
np.sin(a)
array([ 0.84147098,  0.90929743,  0.14112001, -0.7568025 ])

Linear Algebra

Reference docs (https://docs.scipy.org/doc/numpy/reference/routines.linalg.html)

Determinant、Trace、Singular Vector Decomposition、Eigenvalues、Matrix Norm、Inverse Etc…

matmul()方法，matrix multiply的缩写，就是将两个矩阵相乘的方法。

1
2
3
4
5
6
7
8
9
10
11
12
a = np.ones((2,3))
print(a)
[[1. 1. 1.]
 [1. 1. 1.]]
b = np.full((3,2), 2)
print(b)
[[2 2]
 [2 2]
 [2 2]]
np.matmul(a,b)
array([[6., 6.],
       [6., 6.]])
Find the determinant

也就是计算矩阵的行列式的值，这里我们先新建一个3x3的E，然后计算它的值，显然为1

1
2
3
c = np.identity(3)
np.linalg.det(c)
1.0

Statistics

1
2
3
4
stats = np.array([[1,2,3],[4,5,6]])
stats
array([[1, 2, 3],
       [4, 5, 6]])

获得整个矩阵当中的最小值

1
2
np.min(stats)
1

axis = 1代表行就是每一行中的最小值

1
2
np.min(stats, axis=1)
array([1, 4])

获得最大值

1
2
np.max(stats)
6

获得整个矩阵当中的最最大，也就是每一行中的最大值

1
2
np.max(stats, axis=1)
array([3, 6])

获得

1
2
np.sum(stats, axis=0)
array([5, 7, 9])
1
2
np.sum(stats, axis=1)
array([6, 15])

Reorganizing Arrays (reshape, vstack, hstack)

stack(),hstack(),vstack()详解

reshape()

reshape()就是改变当前矩阵的结构，也就是说本来是2x4的矩阵，现在我可以把它变成 4x2 的矩阵

注意了，变换前后，数据个数是无法改变的，我们不能把2x4的矩阵变成3x2的矩阵！

1
2
3
4
5
6
7
8
9
10
11
before = np.array([[1,2,3,4],[5,6,7,8]])
print(before)
[[1 2 3 4]
 [5 6 7 8]]

after = before.reshape((4,2))
print(after)
[[1 2]
 [3 4]
 [5 6]
 [7 8]]

vstack()

vstack()是一种拼接数组的方法

语法

numpy.vstack(tup)
垂直堆叠数组（行方式）。

参数：

除了第一个轴（行）之外，数组必须具有相同的形状。
一维数组必须具有相同的长度。

返回：
返回堆叠的数组
通过堆叠给定的数组最后形成的数组将至少为二维的。

1
2
3
4
5
6
7
8
9
# Vertically stacking vectors
v1 = np.array([1,2,3,4])
v2 = np.array([5,6,7,8])

np.vstack([v1,v2,v1,v2])
array([[1, 2, 3, 4],
       [5, 6, 7, 8],
       [1, 2, 3, 4],
       [5, 6, 7, 8]])

hstack()

按顺序堆叠数组（列式）

除了第二轴（列）之外的所有阵列必须具有相同的形状。

1
2
3
4
5
6
7
8
9
10
11
12
# Horizontal  stack
h1 = np.ones((2,4))
print(h1)
[[1. 1. 1. 1.]
 [1. 1. 1. 1.]]
h2 = np.zeros((2,2))
print(h2)
[[0. 0.]
 [0. 0.]]
np.hstack((h1,h2))
array([[1., 1., 1., 1., 0., 0.],
       [1., 1., 1., 1., 0., 0.]])

Miscellaneous

Load data in from a file

data.txt:

1
2
3
1,13,21,11,196,75,4,3,34,6,7,8,0,1,2,3,4,5
3,42,12,33,766,75,4,55,6,4,3,4,5,6,7,0,11,12
1,22,33,11,999,11,2,1,78,0,1,2,9,8,7,1,76,88

我们从这个文件中读入信息并进行整理：

按照分隔符把txt中的数据分开，然后把字符串都转换成int型

1
2
3
filedata = np.genfromtxt('data.txt', delimiter=',')
filedata = filedata.astype('int32')
print(filedata)
1
2
3
[[  1  13  21  11 196  75   4   3  34   6   7   8   0   1   2   3   4   5]
 [  3  42  12  33 766  75   4  55   6   4   3   4   5   6   7   0  11  12]
 [  1  22  33  11 999  11   2   1  78   0   1   2   9   8   7   1  76  88]]

Advanced Indexing and Boolean Masking

对数据进行筛选，50-100 之间的数给 False，此外给True，~符号代表取反

1
(~((filedata > 50) & (filedata < 100)))
1
2
3
4
5
6
array([[ True,  True,  True,  True,  True, False,  True,  True,  True,
         True,  True,  True,  True,  True,  True,  True,  True,  True],
       [ True,  True,  True,  True,  True, False,  True, False,  True,
         True,  True,  True,  True,  True,  True,  True,  True,  True],
       [ True,  True,  True,  True,  True,  True,  True,  True, False,
         True,  True,  True,  True,  True,  True,  True, False, False]])
-------------本文结束，感谢您的阅读-------------