Multiple_and_Polynomial_Regression

Posted on
Words count in article: 2.9k | Reading time ≈ 11

Multiple and Polynomial Regression

学习自 Udemy课程以及博客 https://www.jianshu.com/p/82966686c68c

Multiple Regression 多元回归

Intuition

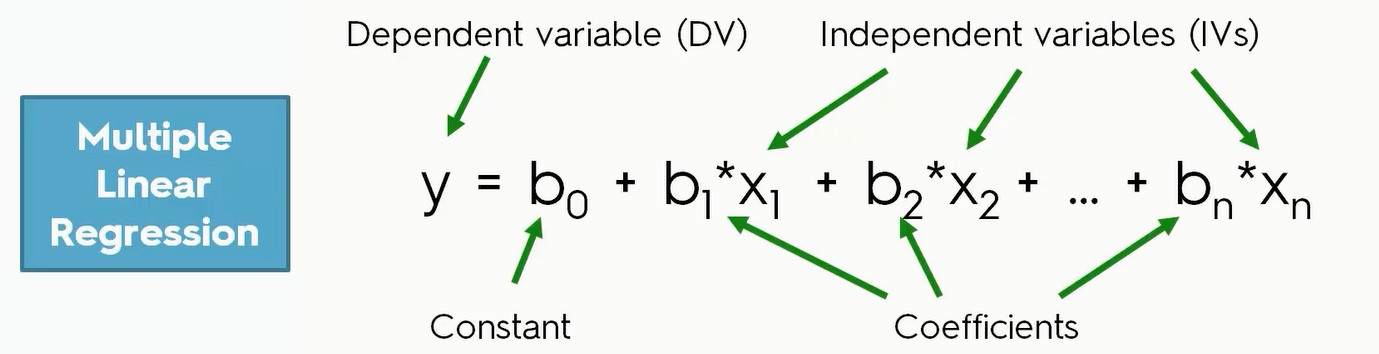
我们来看着这次的数据集。Profit是我们要预测的量，剩下的R&D Spend 、Marketing 、State 是自变量。我们要做的是根据数据集来构建一个线性回归模型。

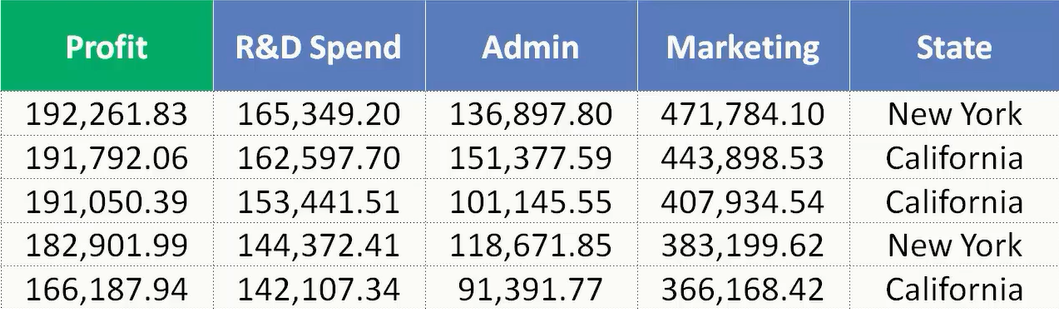
每一个自变量就对应一个 $x_i$ 所以我们可以写出$y = b_0+b_1x_1+b_2x_2+b_3x_3…$ ,但是像State这样的量怎么用来计算呢？

我们需要引入虚拟变量(Dummy Variables) 的概念用以反映质的属性的一个人工变量，是量化了的自变量，通常取值为0或1。引入哑变量可使线形回归模型变得更复杂，但对问题描述更简明，一个方程能达到两个方程的作用，而且接近现实。例如，反映文化程度的虚拟变量可取为：1:本科学历；0：非本科学历

一般地，在虚拟变量的设置中：基础类型、肯定类型取值为1；比较类型，否定类型取值为0。

为什么要dummy化

  • 若用数字1-12表示1-12月，那么就潜在表示了12月和1月差的很远，其实离的很近

  • 若用离散数字表示一地域，假如用数字1-23表示23个省，那么数字潜在的意思是，相邻的数字代表的省比较相似，差距的数字表示的省不相似，然而并没有这个意思。所以用单纯用离散的数字表示类别可能会影响后面回归或分类的精度

模型中引入虚拟变量的作用：

1、分离异常因素的影响

2、检验不同属性类型对因变量的作用，例如工资模型中的文化程度、季节对销售额的影响。

3、提高模型的精度，相当于将不同属性的样本合并，扩大了样本容量（增加了误差自由度，从而降低了误差方差）

另外要注意的是，dummy化不要冗余，比如有1-23个省，我们用22个0，1变量就可以表示，若22个变量都是0则表示第23个省。

在这个数据集当中，我们可以把State转换成Dummy Variables。比如下图。但事实上，我们只需要选择一列即可，因为这里只有New York和California两个选择。

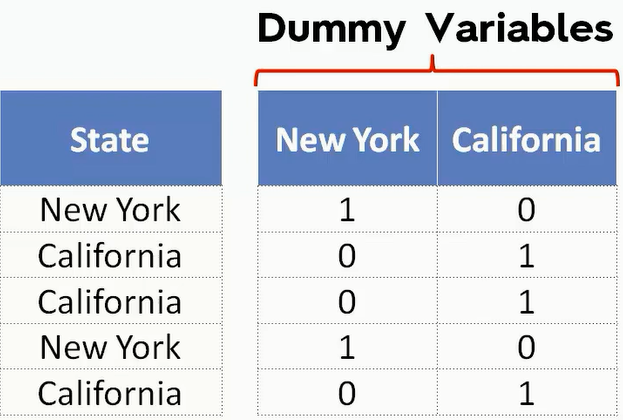
那么我们可以把拟合线的公式这样来写：$y=b_0+b_1x_1+b_2x_2+b_3x_3+b_4D_1$

当有100个互斥值的时候我们需要99个Dummy Variables，这样当所有Dummy Variable=0的时候就代表了第100个值

如何创建一个模型

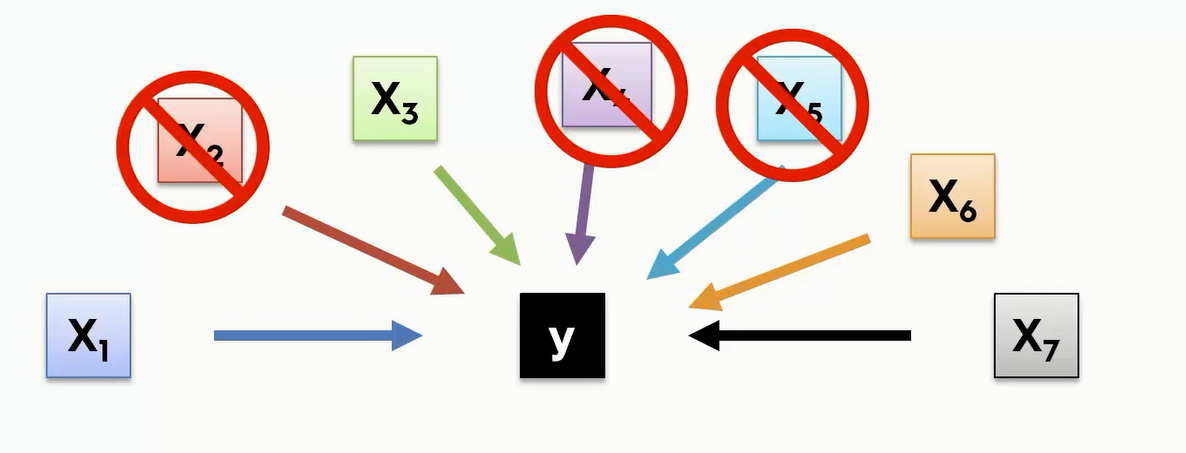
拿到数据以后我们不能讲每一列都当作一个维度来加入到这个模型中，也不能将大多数的列都删除，这样就会让模型变得不稳定。

数学建模有五种方法，第2-4种是逐步回归思路，是比较科学和系统的

  • All - in
  • Backward Elimination
  • Forward Selection
  • Bidirectional Elimination
  • Score Comparison

All-in

第一种我们要将所有的变量都加入到模型当中去。

Backward Elimination(后向逐步回归)

所有变量均放入模型，之后尝试将其中一个自变量从模型中剔除，看整个模型解释因变量的变异是否有显著变化，之后将对残差平方和贡献较小的变量剔除；此过程不断迭代，直到没有自变量符合剔除的条件。

  • Step1： Select a significance level to stay in the model（SL=0.05) SL代表显著性。统计学上通常把低于5%概率事件看做小概率事件，5%就是significance level，也就是认定是异常的界限。
  • Step2：使用所有的自变量来拟合出一个模型
  • Step3: 对于这个模型当中的每一个自变量都来计算它的P值（P-value）,来显示它对我们模型有多大的影响力，然后我们取这个最高的P值，假设这个P>SL,就继续往第四步，否则就算法结束。
    • 关于p-value https://www.cnblogs.com/lijingblog/p/11043513.html
    • https://www.mathbootcamps.com/what-is-a-p-value/
    • 【为什么小于0.05就很重要？】大部分时候，我们假设错误拒绝H0的概率为0.05，所以如果p值小于0.05，说明错误拒绝H0的概率很低，则我们有理由相信H0本身就是错误的，而非检验错误导致。大部分时候p-value用于检验独立变量与输入变量的关系，H0假设通常为假设两者没有关系，所以若p值小于0.05，则可以推翻H0（两者没有关系），推出H1（两者有关系）。
    • 所以说当 p-value大于SL的时候，我们就要移除这个predictor
  • Step4:最高的P值对应的那个自变量我们就要将它从我们的模型中去除
  • 去除了一个自变量后，在用剩下的自变量重新对模型进行拟合

因此这里就是一个第三步到第五步的一个循环，直到所有剩下的P值都比SL要小，这样就说明模型已经拟合好了

Forward Selection(前向逐步回归)

向前法的思想是变量由少到多，属于贪心算法，每次增加一个，直至没有可引入的变量为止。具体步骤如下。

  • Step1： Select a significance level to enter the model(e.g. SL = 0.05)
  • Step2：我们在这边对每个自变量 $x_n$ 都进行简单线性回归拟合，分别得到它们的P值，然后取得它们中最低的。
  • Step3：对于这个最低的P值，我们的结论就是这个自变量它对我们将要拟合的模型的影响是最大的，所以说，我们会保留这个自变量
  • Step4：我们再看剩下的自变量当中加上哪一个会给我们带来最小的P值，假如说新的P值比我们之前定义的SL小，那就重新回到第三步，也就是第三步又加入了一个新的变量然后在接下来剩下的变量当中，重新找最大的P值，然后继续加到模型当中，

Bidirectional Elimination

所谓双向淘汰，其实就是对之前的两种算法的结合

  • Step1：我们需要选择两个显著性门槛：一个旧的变量是否应该被剔除和一个新的还没有被采纳的变量是否应当进入我们的模型。(e.g.:SLENTER = 0.05,SLSTAY = 0.05)
  • Step2:我们要进行顺向选择，来决定是否采纳一个新的自变量。(new variables must have:P<SLENTER to enter)
  • Step3: 要进行反向淘汰，也就是我们可能要剔除旧的变量 (old variables must have P<SLSTAY to stay)
  • Step4：在第二第三步之间进行循环，由于已经定义了两个门槛，但出现新的出不去，旧的进不来时，就说明模型已经拟合好了。

All Possible Models 信息量比较

对于所有可能的模型，我们对它们进行逐一的打分，对于多元线性回归，如果有N个自变量，那么就有$2^N-1$个不同的模型

  • Step1: Select a criterion of goodness of fit(e.g. Akaike criterion)
  • Step2: Construct All Possible Regression Models: $2^N-1$ total combinations
  • Step3: Select the one with the best criterion

Fin: Your model is Ready

那这里就会有一个问题，如果N很大的时候，模型的数量就会非常庞大。所以说这个方法虽然直觉上很好理解，但自变量数量很大时就不适合使用这种方法。

代码：

对于上面的数据集，我们首先要做一些简单的数据处理：

1
2
3
4
5
6
7
8
dataset = pd.read_csv('50_Startups.csv')
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, -1].values

from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OneHotEncoder
ct = ColumnTransformer(transformers=[('encoder', OneHotEncoder(), [3])], remainder='passthrough')
X = np.array(ct.fit_transform(X))

目的就是将三个州化成0、1这样的dummy variable

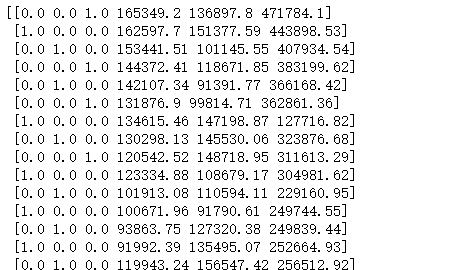
随后我们就可以交给线性回归模型去训练了。注意，交给回归模型训练不需要删除一列dummy variable，也不需要选择哪一个variable的影响最大。因为这些python都帮我们做好了，事实上我们只需要两三行代码就可以完成模型训练了。所以我们更本不用担心变量的选取是否准确

接下来是将数据集分为训练集和测试集并交给LinearRegression进行训练：

1
2
3
4
5
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)
from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor.fit(X_train, y_train)

训练完成之后，我们只要对测试集进行预测即可

1
2
3
y_pred = regressor.predict(X_test)
np.set_printoptions(precision=2)# 这边是对打印的数据格式进行一个设置，也就是在两个小数之间添加一个逗号
print(np.concatenate((y_pred.reshape(len(y_pred),1), y_test.reshape(len(y_test),1)),1))

reshape就是将横向的向量变成竖向的向量。len(y_pred) 计算向量长度，1就代表按照y轴排列，也就是竖向排列

最后预测出来的结果和真实的结果进行一个比较

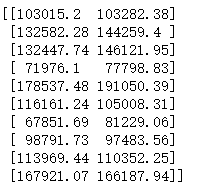
Polynomial Regression 多项式回归

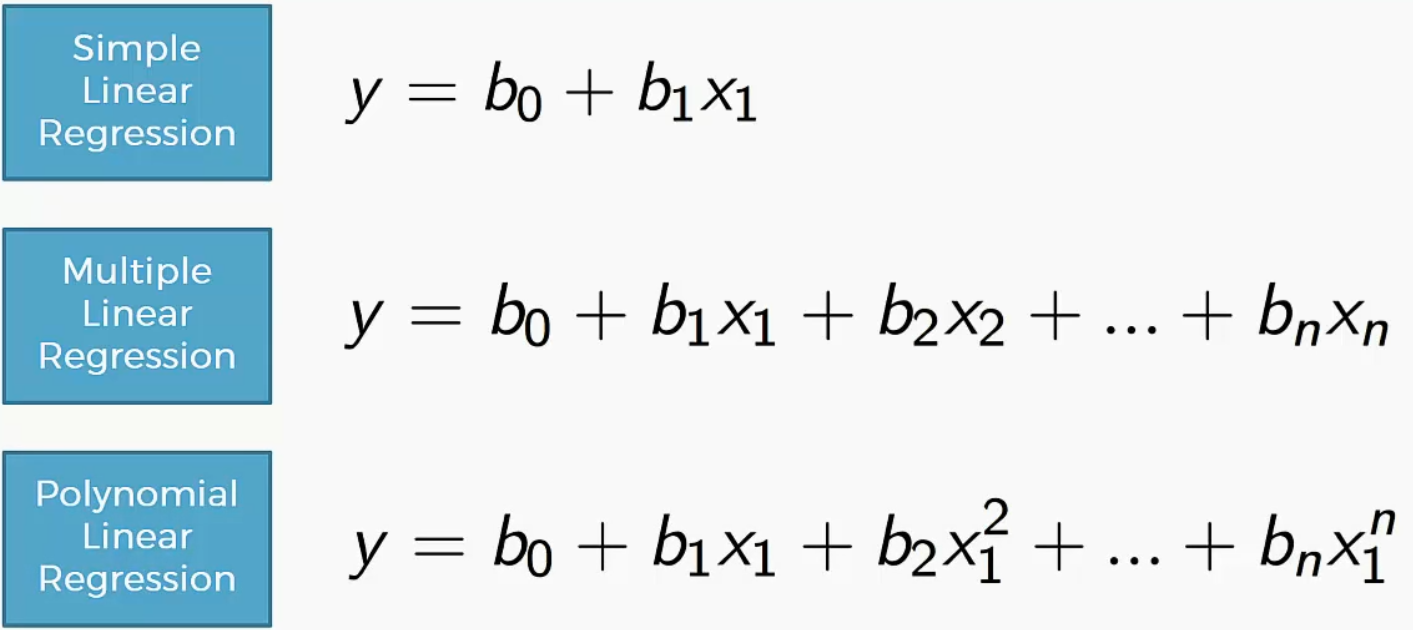
对于抛物线来说，线性回归是没有办法模拟出来的。但是可以用多项式回归模拟出来

这个表达式和多元线性回归非常像，唯一的区别就是多项式线性回归中存在很多次方项，而多元线性回归中是多个变量。实际上这里可以把多元线性回归中的多个变量理解成多项式中的$x_n^2$ .所谓线性，看的是 $b_0$一直到$b_n$ 这些参数的一个线性组合，跟自变量是否线性其实没什么关系，因此这种情况依然是线性的。当然也存在非线性的多项式回归，比如这里假设公式是 $y=b_0/b_2+b_3x_3$ 这时候就不是关于 $b_0$ 一直到 $b_n$ 这些参数的线性表达式了

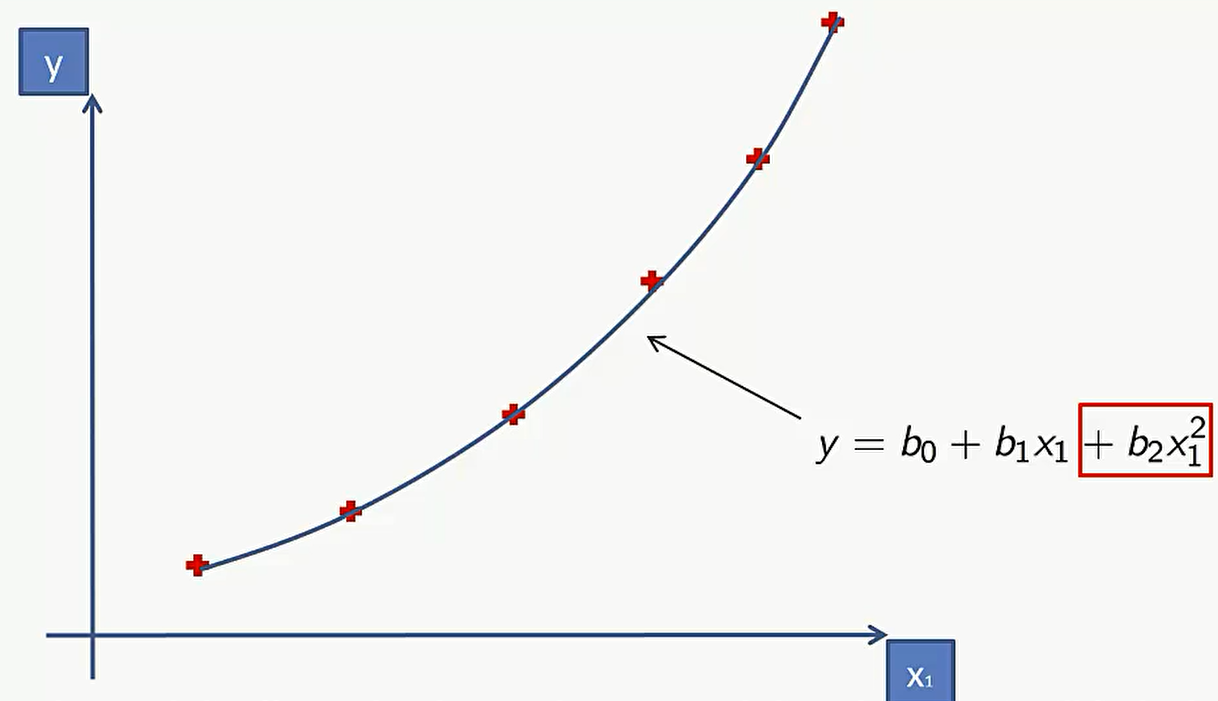
多项式模型在研究病毒传播等大流行病中能比简单线性回归模型更好的完成任务。

代码

现在有一个数据集：

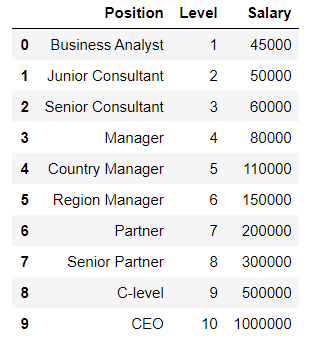
我们选择x和y,其中x就是level，y是Salary

1
2
3
dataset = pd.read_csv('Position_Salaries.csv')
X = dataset.iloc[:, 1:-1].values
y = dataset.iloc[:, -1].values

接下来我们做一个 Linear Regression和 Polynomial Regression的对比

Linear Regression

1
2
3
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X, y)

Polynomial Regression

1
2
3
4
5
6
7
from sklearn.preprocessing import PolynomialFeatures
# 也就是多项式的最高次数
poly_reg = PolynomialFeatures(degree = 2)
# 然后将一个X转化成 x_poly,也就是将原来的Level变成一个新的feature matrix (x+x^2)
X_poly = poly_reg.fit_transform(X)
lin_reg_2 = LinearRegression()
lin_reg_2.fit(X_poly, y)

然后我们来看看两种方式的拟合结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Visualising the Linear Regression results
plt.scatter(X, y, c='r')
plt.plot(X, lin_reg.predict(X), c='b')
plt.title('Truth or Bluff (Linear Regression)')
plt.xlabel('Position Level')
plt.ylabel('Salary')
plt.show()
# Visualising the Polynomial Regression results
plt.scatter(X, y, c='r')
plt.plot(X, lin_reg.predict(X), c='b')
plt.plot(X, lin_reg2.predict(poly_reg.fit_transform(X)), c='b')
plt.title('Truth or Bluff (Polynomial Regression)')
plt.xlabel('Position Level')
plt.ylabel('Salary')
plt.show()

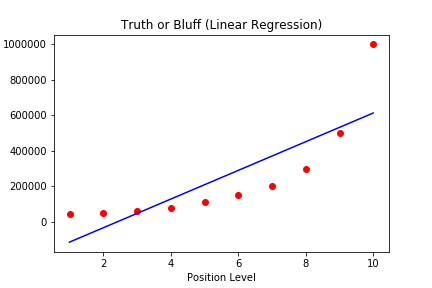
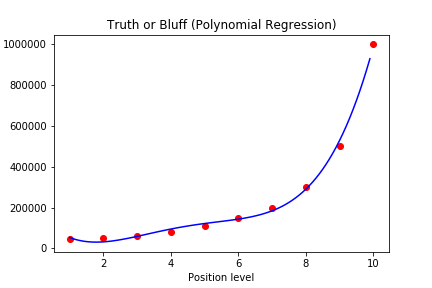
我们看到是Polynomial regression 拟合的更好一些，但也不是完全贴合

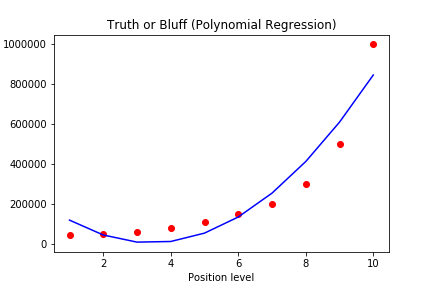
于是我们使用更高阶来试试，将poly_reg 改为 PolynomialFeatures(degree = 4)，并用plt对图像进行一个优化，得到如下的拟合曲线。发现基本能够完全贴合

1
2
3
4
5
6
7
8
X_grid = np.arange(min(X), max(X), 0.1)
X_grid = X_grid.reshape((len(X_grid), 1))
plt.scatter(X, y, color = 'red')
plt.plot(X_grid, lin_reg_2.predict(poly_reg.fit_transform(X_grid)), color = 'blue')
plt.title('Truth or Bluff (Polynomial Regression)')
plt.xlabel('Position level')
plt.ylabel('Salary')
plt.show()

-------------本文结束，感谢您的阅读-------------