Simple Linear Regression

Intuition

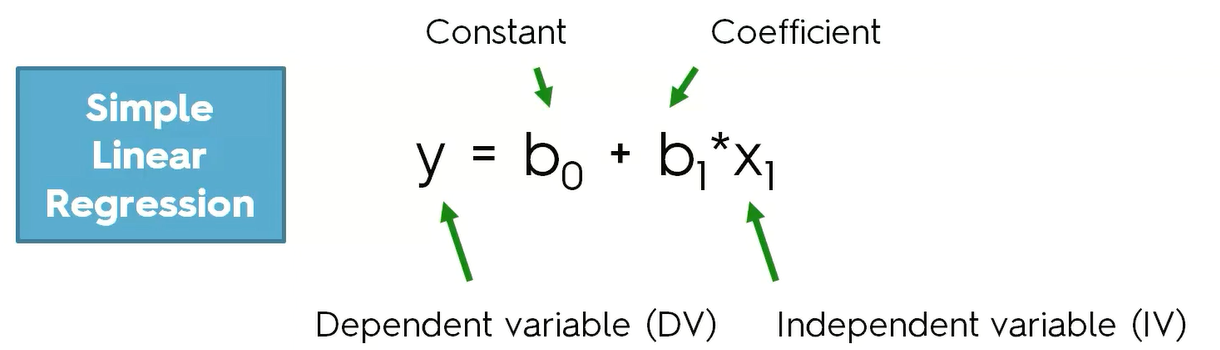
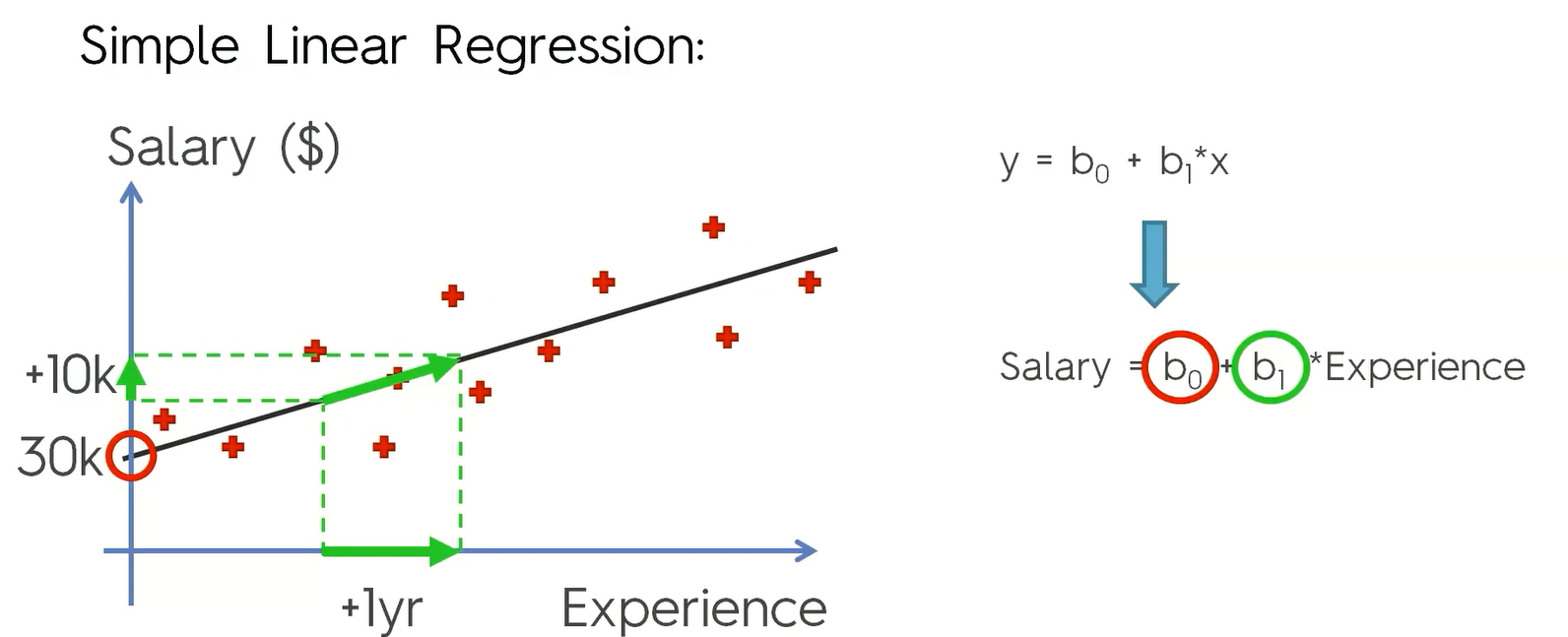
线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计。在散点图上绘制一条直线，使得这条直线尽可能多通过数据点，要求出最佳拟合线需要求出回归方程y=a+bx，其中a为截距，b为回归系数，在方程中使得y的实际观察值与每个x相对应的y

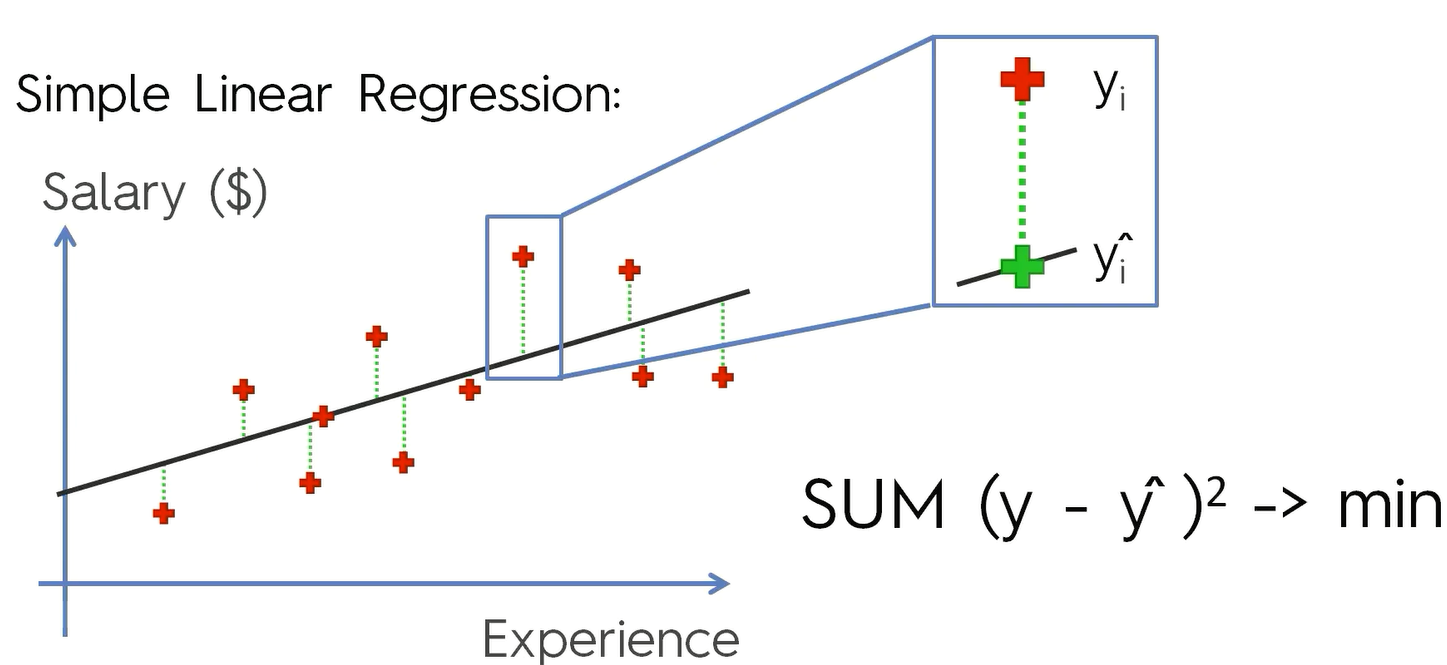
那么怎么来拟合这条曲线呢？事实上我们需要画很多很多的曲线，然后$\sum (y_i-\hat y_i)$的最小值。当$\sum (y_i-\hat y_i)$取得最小时，这条线就是我们需要得拟合直线

Steps

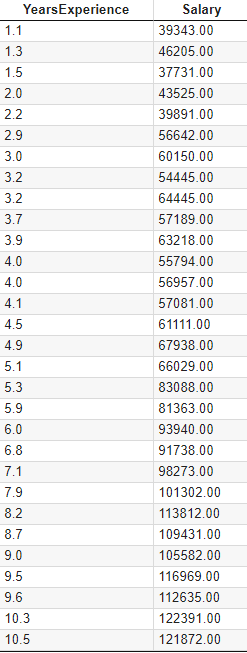
下面来介绍实现简单线性回归的代码。我们使用一个简单的实例：工作年数与薪水多少的关系。下面是我们的原始数据集：第一列代表了员工的工作年数，第二列代表了员工当前的薪水。我们的目标很简单，就是创建一个简单线性回归模型，经过训练之后，得到工作年数和薪水之间的关系，然后根据一些员工的工作年数来预测一些员工的薪水

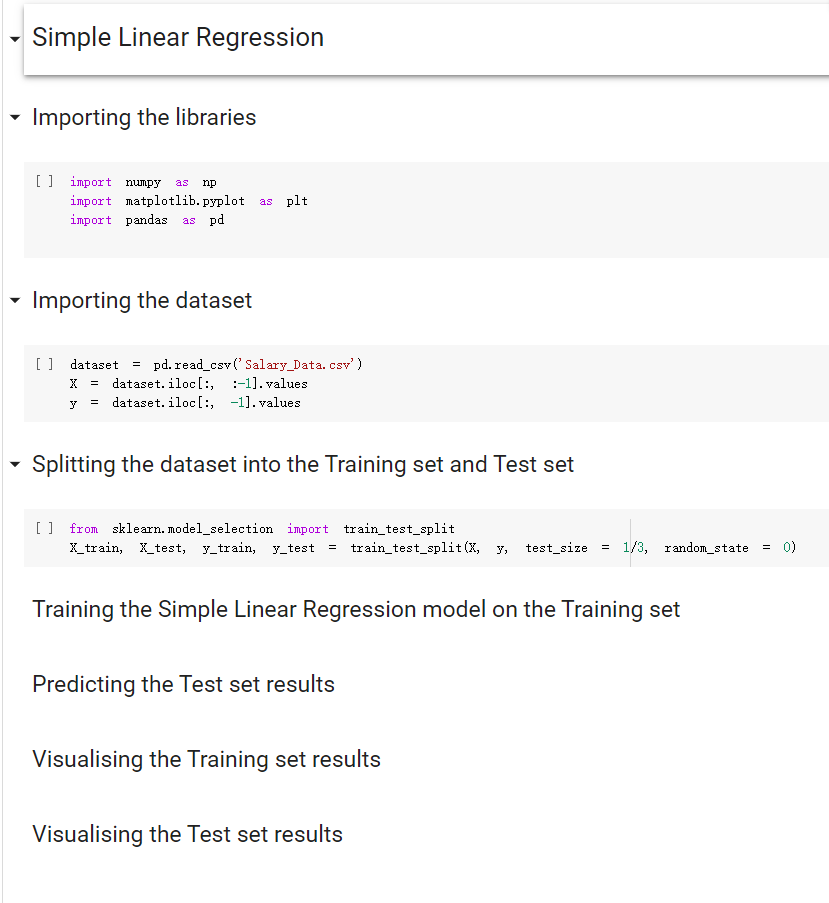
这是我们的模板：

现在我们来训练简单线性回归模型。很简单我们导入一个库即可。首先我们从sklearn中导入LinearRegression类，然后令 regressor等于一个LinearRegression类。最后让fit()方法，填入训练集的x,y就能拟合出简单线性回归模型了

1
2
3

from sklearn.linear_model import LinearRegression
regressor =  LinearRegression()
regressor.fit(X_train,y_train)

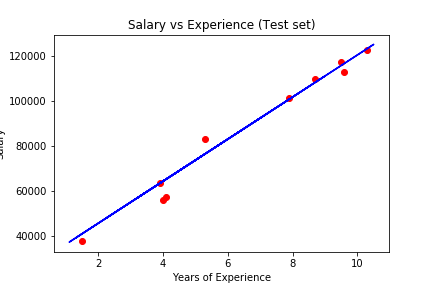
然后我们要把这个训练好的简单线性回归模型放到测试集当中去，用它来预测测试集当中Years对应的Salary值。很简单我们只要一句代码即可

1	y_pred = regressor.predict(X_test)

array([ 40835.10590871, 123079.39940819, 65134.55626083, 63265.36777221, 115602.64545369, 108125.8914992 , 116537.23969801, 64199.96201652, 76349.68719258, 100649.1375447 ])

这就是预测后的结果。我们令其为 y_pred

最后我们来可视化训练的结果。

plt.scatter(X_train, y_train, color = 'red')
plt.plot(X_train, regressor.predict(X_train), color = 'blue')
plt.title('Salary vs Experience (Training set)')
plt.xlabel('Years of Experience')
plt.ylabel('Salary')
plt.show()

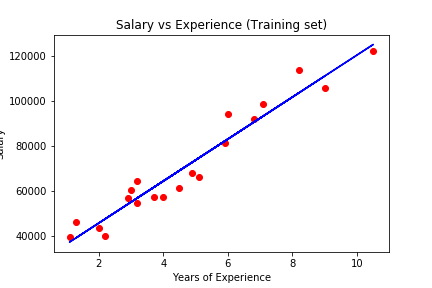
plt.scatter(X_test, y_test, color = 'red')
plt.plot(X_train, regressor.predict(X_train), color = 'blue')
plt.title('Salary vs Experience (Test set)')
plt.xlabel('Years of Experience')
plt.ylabel('Salary')
plt.show()