n皇后问题

Posted on
Words count in article: 1.7k | Reading time ≈ 7

n皇后问题

在n×n的棋盘上放置彼此不受攻击的n个皇后。按照国际象棋的规则，皇后可以攻击与之在同一行、同一列、同一斜线上的棋子。设计算法在n×n的棋盘上放置n个皇后，使其彼此不受攻击。在第i行第j列放置一个皇后，那么第i行的其他位置（同行），那么第j列的其他位置（同列），同一斜线上的其他位置，都不能放置皇后。

我们要判断第t个皇后是否满足条件，就是在t-1 个皇后已经满足条件的情况下来进行判断。只要有一个冲突，这个位置就无法放置第t个皇后。

(1）定义问题的解空间

n皇后问题解的形式为n元组：${x_1，x_2，…，x_i，…，x_n}$，分量 $x_i$表示第i个皇后放置在第i行第 $x_i$ 列，$x_i$ 的取值为1，2，…，n。例如$x_2=5$，表示第2个皇后放置在第2行第5列。

显约束为不同行。

(2）解空间的组织结构

n皇后问题的解空间是一棵m（m=n）叉树，树的深度为n。因为我这里是一个方格棋盘，所以 m是等于n 的

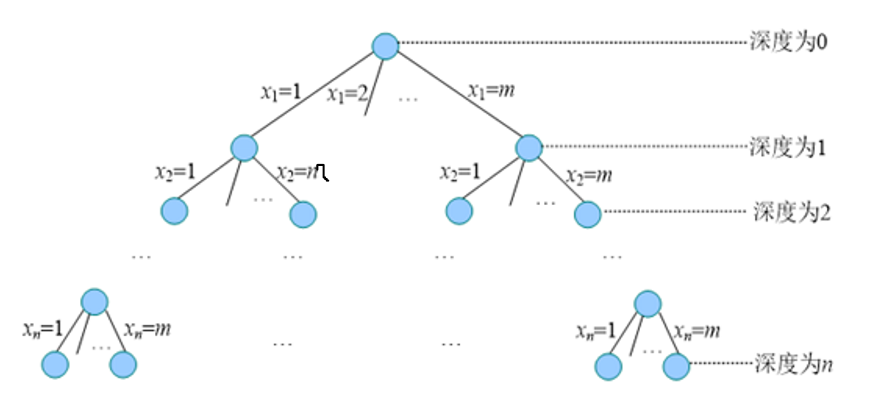
这是一个很庞大的树，我们要懂得如何剪枝。

(3)搜索解空间

· 约束条件

在第t行放置第t个皇后时，第t个皇后的位置不能和前t−1个皇后同列、同斜线。第i个皇后和第j个皇后不同列，即$x_i!=x_j$，并且不同斜线$|i-j|!=|x_i-x_j|$。 如果不满足条件，那就回溯，重新分配位置

· 限界条件

该问题不存在放置方案好坏的情况，所以不需要设置限界条件

算法分析

时间复杂度

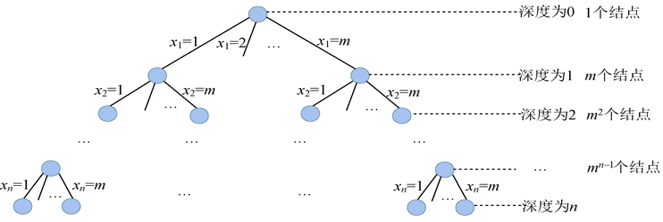
除了最后一层外， 有$1+n+n^2+\cdots +n^{n-1}=(n^n-1)/(n-1)\approx n^{n-1}$个结点需要扩展 ， 而这些结点每个都要扩展 n 个分支， 总的分支个数为$n^n$， 每个分支都判断约束函数， 判断约束条件需要O(n)的时间， 因此耗时 $O(n^{n+1})$。在叶子结点处输出当前最优解需要耗时 O(n), 在最坏情况下回搜索到每一个叶子结点 ， 叶子个数为 $n^n$, 故耗时为 $O(n^{n+1})$。因此，时间复杂度为 $O(n^{n+1})$。

空间复杂度：

在所搜过程中的任何时刻，仅保留从开始结点到当前扩展结点的路径，从开始结点起最长的路径为n。程序中使用x[]数组记录该最长路径作为可行解，所以该算法的空间复杂度为O(n)。

代码一览

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
//program 5-4
#include<iostream>
#include<cmath>   //求绝对值函数需要引入该头文件
#define M 105
using namespace std;

int n;//n表示n个皇后
int x[M];  //x[i]表示第i个皇后放置在第i行第x[i]列
long long countn;    //countn表示n皇后问题可行解的个数

bool Place(int t) //判断第t个皇后能否放置在第i个位置
{
    bool ok=true;
    for(int j=1;j<t;j++)   
    //判断该位置的皇后是否与前面t-1个已经放置的皇后冲突
    {
       if(x[t]==x[j]||t-j==fabs(x[t]-x[j]))//判断列、对角线是否冲突
       {
           ok=false;
           break;
       }
    }
    return ok;
}

void Backtrack(int t) //回溯
{
    if(t>n)  
    //如果当前位置为n,则表示已经找到了问题的一个解
    {
        countn++; //用来统计与多少种求解方案
        for(int i=1; i<=n;i++) //打印选择的路径
          cout<<x[i]<<" ";
        cout<<endl;
        cout<<"----------"<<endl;
    }
    else
        for(int i=1;i<=n;i++)
        //分别判断n个分支,特别注意i不要定义为全局变量,否则递归调用有问题
        {
            x[t]=i;
            if(Place(t)) 
                //判断x[t] 能不能等于i，如果不能那么回溯，更新位置
                Backtrack(t+1); //如果不冲突的话进行下一行的搜索
        }
}

int main()
{
    cout<<"请输入皇后的个数 n:";
    cin>>n;
    countn=0;
    Backtrack(1);
    cout <<"答案的个数是: "<<countn<< endl;
    return 0;
}

但是这样的算法会出现很多的无效判断。因为当 第一个节点已经选1的时候，接下来的节点还需要重复判断选1是否可行，所以我们还需要优化

算法优化拓展：

以上求解方法的解空间为m叉树，m=n，解空间过于庞大，所以时间复杂度很高，算法效率当然会降低。

解空间越小，算法效率越高。如果能够缩小解空间，则可以提高效率。

n皇后问题采用不同行作为显约束，隐约束为不同列、不同斜线，解空间为m叉树。4皇后问题，显约束为不同行的解空间树如图。

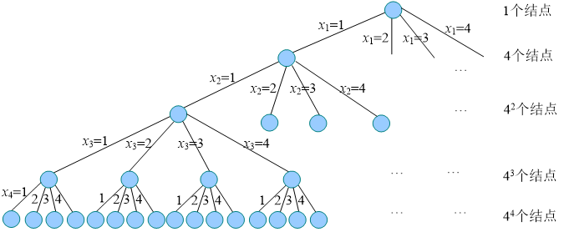
显约束可以控制解空间大小，隐约束用于判定可行解或最优解。如果把显约束定为不同行、不同列，隐约束为不同斜线。4皇后问题，显约束为不同行、不同列的解空间树如图。解空间变小了好多！从树根倒也则的每一个可能解其实是一个排列。我们找解就是从这些排列中取寻找。

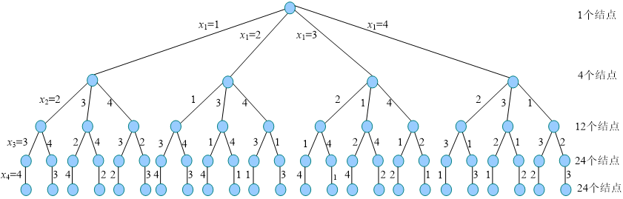
那么，怎么才能找到这些排列呢？我们需要用到排列树。

排列树的设计理念：有n个元素 1，2，3….n

1) 1与1 交换， 求(2,3,…,n) 的排列
2) 2与1 交换， 求(1,3,…n) 的排列
…
n) n与1 交换， 求(2,3,…,1) 的排列

这样每个数开头一次，递归求解剩下的序列的排列， 即可得到n个数的全排列

我们可以很容易得到3个数的排列：
(1) 1 与1 交换， 求 (2, 3) 的排列。
(2, 3) 的排列是 (2, 3) 和 (3, 2), 得到 l 开头的排列： 1 2 3, 1 3 2。

(2) 2 与1 交换， 求 (1, 3) 的排列。
(I, 3) 的排列是(I, 3) 和 (3, I), 得到 2 开头的排列： 2 1 3, 2 3 1。

(3) 3 与 1 交换， 求 (2, 1) 的排列。
(2, l) 的排列是 (2, 1) 和(1, 2), 得到3 开头的排列：321, 312。

那么怎么用程序实现呢？

代码一览

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
//program 5-5-1
#include <iostream>
#define MX 50
using namespace std;
int x[MX];         //解分量
int n;

void myarray(int t)
{
    if(t>n)
    {
        for(int i=1;i<=n;i++) // 输出排列
            cout<<x[i]<<" ";
        cout<<endl;

        return ;
    }
    for(int i=t;i<=n;i++)  // 枚举
    {
       swap(x[t],x[i]);  // 交换
       myarray(t+1);  // 继续深搜
       swap(x[t],x[i]); // 恢复
    }
}

int main()
{
    cout << "输入排列的元素个数n(求1..n的排列):" << endl;
    cin>>n;
    for(int i=1;i<=n;i++) //初始化
       x[i]=i;
    myarray(1);
    return 0;
}
-------------本文结束，感谢您的阅读-------------