插入排序和冒泡排序

Posted on | In
Words count in article: 1.6k | Reading time ≈ 6

插入排序和冒泡排序

插入排序

直接插入排序是最简单的排序方法，每次将一个待排序的记录，插入到已经排好序的数据序列当中，得到一个新的长度增1的有序表

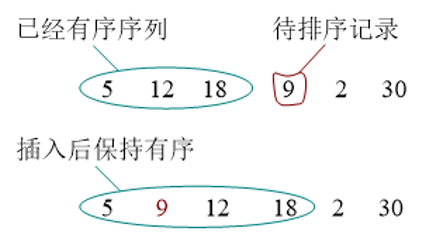
算法步骤

1） 设待排序的记录存储在数组 r[1],r[2]…r[n] 中，可以把第一个记录$r[1]$ 看作一个有序序列

2） 依次将 r[i](i=2,….,n) 插入到已经排好序的序列 r[1,….,i-1] 当中，并保持有序性， 我们看到 r[0] 是空的，它的作用是保存将要插入到数组当中的数字的。

比如2比12小，那么 r[0] = 2 ,12 后移，再将2 从r[0]移到r[1].

16比12大，什么都不需要做。

30比16大，什么也不需要做。

28比30小，令r[0] = 28 ,30 往后移动一格，再让28和16比，因为28>16 所以16 不动，28插入到16和30 之间。

非递减即为允许相等的递增

算法分析

时间复杂度

最好情况下，待排序序列本身是正序的(如待排序序列是非递减的，题目要求也是非递减排序) ， 每个记录只需要和前一个记录比较一次， 不小于前一个记录， 则什么都不用做， 总的比较次数为

$\Sigma _{i=2}^n 1 = n-1$

那么最好的情况下直接插入排序的时间复杂度为$O(n)$

最坏情况下，待排序序列本身是逆序的（如待排序序列是非递增的，题目要求是非递减排序），每个记录都需要比较 i 次，包括和前 i-1 记录比较，并和哨兵 r[O]比较，总的比较次数为：

$\Sigma_{i=2}^n i = \frac{(n+2)(n-1)}{2}$

最坏情况下，直接插入排序的事件复杂度为 $O(n^2)$

平均情况下，若大排序序列出现各种情况的概率均等，则可取最好的情况和最坏的情况的平均值。平均情况下，直接插入排序的时间复杂度也为 $O(n^2)$

空间复杂度

直接插入排序使用了一个辅助空间r[0] ,空间复杂度为 $O(1)$

稳定性

直接插入排序时，已经有序的序列中的记录比待排序记录大时才向后移动，和待排序记录相等时不向后移动， 因此两个相等的记录在排序前后的位置顺序是不变的。例如， 上例中排序前16在16*之前， 排序后16仍在16*之前。 因此直接插入排序是稳定的排序方法。
直接插入排序每次将待排序记录插入到一个有序序列中，在有序序列中查找待排序记录 的插入位置时，折半查找的方法比顺序查找效率更高，采用折半查找插入位置的插入排序称为折半插入排序， 有兴趣的读者可以自己动手试试。

练习题

  • 什么排序算法可能会出现：在最后一趟开始之前，所有元素都不在最终位置上这一情况？ 直接排序算法，最后一趟待排序元素是最小的，之前所有位置上的元素都要后移
  • 待排序表为反序时，直接插入排序需要进行 $(n)(n-1)/2$ 次比较(从前往后依次需要1,2,$\cdots$ n-1次) ; 待排序表 为正序的时候，只需进行 n-1 次比较

代码一览

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <iostream>
using namespace std;
#define Maxsize 100

void StraightInsertSort(int r[],int n)  //直接插入排序
{
 	int i,j;
	for(i=2;i<=n;i++)  //r[i]插入有序子表
        if(r[i]<r[i-1]) //r[i]和前一个元素r[i-1]比较
        {
            r[0]=r[i];			//r[i]暂存到r[0]中，r[0]有监视哨的作用
            r[i]=r[i-1];	    //r[i-1]后移一位
            for(j=i-2;r[j]>r[0];j--) //从后向前寻找插入位置,逐个后移，直到找到插入位置
                r[j+1]=r[j];		//r[j]后移一位
            r[j+1]=r[0];		//将r[0]插入到r[j+1]位置
        }
}

int main()
{
    int i,n,r[Maxsize+1];
    cout<<"请输入数列中的元素个数n为："<<endl;
    cin>>n;
    cout<<"请依次输入数列中的元素："<<endl;
    for(i=1;i<=n;i++)
       cin>>r[i];
    StraightInsertSort(r,n);
    cout<<"直接插入排序结果："<<endl;
    for(i=1;i<=n;i++)
       cout<<r[i]<<" ";
    return 0;
}

冒泡排序

冒泡排序是一种最简单的交换排序算法，通过两两比较关键字，如果逆序就交换，使关键字大的记录像泡泡一样冒出来放在尾部。重复执行若干次冒泡排序，最终得到有序序列。

算法步骤

1） 设待排序的记录存储在数组 r[1,…,n ] 当中，首先第一个记录和第二个记录关键字比较，若逆序则交换；然后第二个记录和第三个记录关键字比较，…, 以此类推，直到第 n-1 个记录和第n个记录关键字比较完毕为止。第一趟排序结束，关键字最大的记录在最后一个位置。

2）第二趟排序，对前n-1 个元素进行冒泡排序，关键词次大的记录在n-1 位置

3）重复上述过程，知道某一趟排序中没有进行交换记录为止，说明序列已经有序。

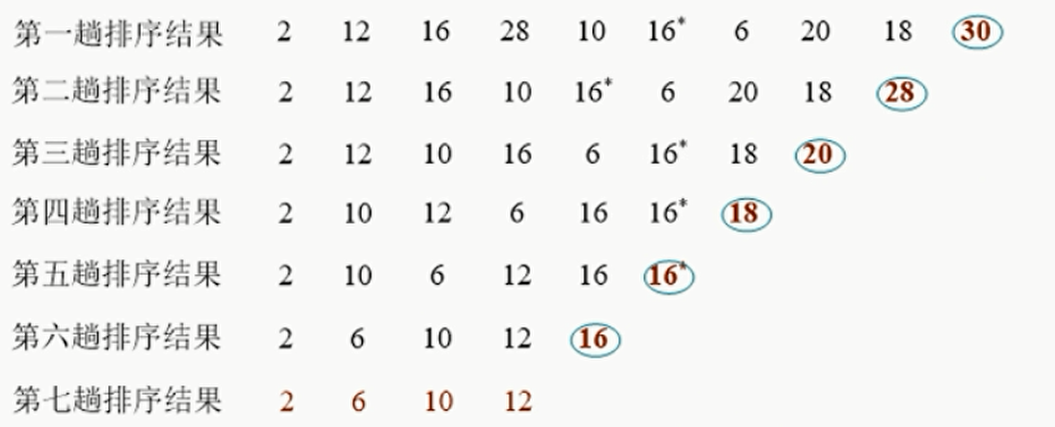
到了第七趟排序的时候，发现没有交换，所以立即停止。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <iostream>
using namespace std;
#define Maxsize 100

void BubbleSort(int r[],int n) //冒泡排序
{
  	int i,j,temp;
  	bool flag;
  	i=n-1;
  	flag=true;
  	while(i>0&&flag)
    {
        flag=false;
        for(j=0;j<i;j++) //进行一趟排序
            if(r[j]>r[j+1])
            {
                flag=true;
                temp=r[j]; //交换两个记录
                r[j]=r[j+1];
                r[j+1]=temp;
            }
        for(j=0;j<=i;j++)//测试每趟排序结果
            cout<<r[j]<<" ";
        cout<<endl;
        i--;
    }
}

int main()
{
    int i,n,r[Maxsize];
    cout<<"请输入数列中的元素个数n为："<<endl;
    cin>>n;
    cout<<"请依次输入数列中的元素："<<endl;
    for(i=0;i<n;i++)
       cin>>r[i];
    BubbleSort(r,n);
    cout<<"冒泡排序结果："<<endl;
    for(i=0;i<n;i++)
       cout<<r[i]<<" ";
    return 0;
}
-------------本文结束，感谢您的阅读-------------