查找
查找算法的性能和下面几个因素有关:
1)算法
2) 数据规模
3)待查关键字在数据表中的位置
4)查找的频率
评价一个查找算法的好坏,一般采用平均查找长度(ASL) 来衡量。分为查找成功的平均查找长度和查找失败的平均查找长度。计算公式:
$ASL = \Sigma_{i=1}^n p_ic_i$
其中,n为数据规模,$p_i$ 为查找第i 个记录的概率,$c_i$ 为查找第i个记录所需要的关键字比较次数。
根据在查找过程中是否对表有修改操作,分为静态查找和动态查找。根据数据结构的不同又分为线性表查找、数表查找和散列表查找。散列表查找是一种比较特殊的查找方式。
线性表的查找非常简单,如果线性表无序,则采用顺序查找,如果线性表有序,则采用二分查找(折半查找)
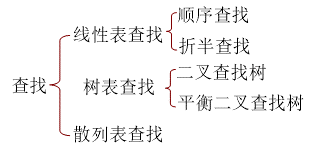
平衡二叉查找树有AVL、tremp、splay、SBT、红黑树等
顺序查找
例如,序列 ${8,12,5,16,55,24,20,18,36,6,50}$ ,用顺序查找法查找 55
1) 初始状态,将序列存储在数组 $r[0…10]$ 中, x=55
2)将 x 与 r[0] 比较,$x\neq r[0]$,则继续比较下一个。如图8-1所示。

算法分析:
1) 时间复杂度
顺序查找最好的情况,一次查找成功,最坏的情况n次查找成功。
假设查找每个关键字的概率均等,即查找概率 $p_i=1/n$ ,查找第i个关键字需要比较i次成功,则查找成功的平均查找长度:
$ASL = \sum{i=1}^np_ic_i=\sum{i=1}^n \frac{1}{n} i = \frac{n+1}{2}$
如果查找的关键字不存在,则每次都会比较n次,时间复杂度为 $O(n)$ m
2) 空间复杂度
算法只使用了一个辅助变量i, 空间复杂度为$O(1)$
1 | int SqSearch(int r[],int n,int x)//顺序查找 |
二分查找
给定n个元素序列,这些元素是有序的(假设为升序),从序列中查找元素x。
用一维数组 S[] 存储该有序序列,设变量low和high表示查找范围的下界和上界,middle表示查找范围的中间位置,x为特定的查找元素。
算法步骤
1) 初始化。 令low = 0,即指向有序数组 $S[]$ 的第一个元素; high = n-1,即指向有序数组 $S[]$ 的最后一个元素
2)判定 $low\leq high$ 是否成立,如果成立,转向第三步,否则算法结束。
3)middle = (low+high)/2 即只想查找范围的中间元素。
4)判断x 与 $S[middle]$ 的关系。如果 $x= S[middle]$ ,则搜索成功,算法结束;如果 $x>S[middle]$ 则令 $low = middle+1$ 否则令 $high = middle-1$ 转向第2步。
算法分析
1) 时间复杂度
二分查找算法,时间复杂度怎么计算呢? 如果用 $T(n)$ 来表示n个有序元素的二分查找算法的事件复杂度,那么: 当n=1 时,需要一次比较 $T(n)=O(1)$
当 $n>1$ 时,带查找元素和中间位置元素比较,需要$O(1)$ 时间,如果比较不成功,那么需要在前半部分或者后半部分搜索,问题的规模缩小了一般,时间复杂度变为$T(n/2)$
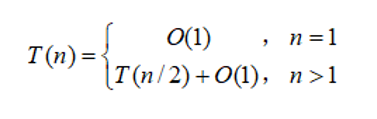
二分查找的非递归算法和递归算法有一样的时间复杂度,均为 $O(logn)$
2) 空间复杂度
二分查找的非递归算法中,变量占用了一些辅助空间,这些辅助空间都是常数阶的,因此空间复杂度为$O(1)$
二分查找递归算法,除了使用一些变量外,递归调用还需要使用栈来实现。
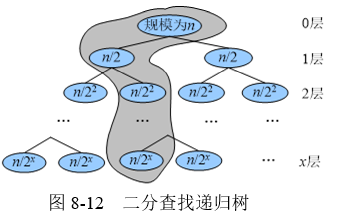
递归调用最重的规模为1,即 $n/2^x=1$ 则 $x=logn$ 设阴影部分时搜所经过的路径,一共经过了log n 个 节点,也就是说递归调用了 log n次。递归算法使用的栈空间为递归树的深度,因此二分查找递归算法的空间复杂度为$O(logn)$
代码一览
1 | int BinarySearch(int s[],int n,int x)//二分查找非递归算法 |