CSAPP信息的表示和存储
怎么阅读CSAPP?
- 首先看一下标题和插图
- 看懂示意图之后做一些 practice problem,有不懂的再去看书本内容
- 用例子来帮助我们理解
上课笔记
main(arg c ,arg v)
argc和argv参数在用命令行编译程序时有用
第一个参数,int型的argc,为整型,用来统计程序运行时发送给main函数的命令行参数的个数
第二个参数,char*型的argv[],为字符串数组,用来存放指向的字符串参数的指针数组,每一个元素指向一个参数。各成员含义如下:argv[0]指向程序运行的全路径名
argv[1]指向在DOS命令行中执行程序名后的第一个字符串
argv[2]指向执行程序名后的第二个字符串
argv[3]指向执行程序名后的第三个字符串
argv[argc]为NULL
shell 中的命令时怎么去运行的
https://www.cnblogs.com/chaoguo1234/p/5724321.html
C中的内存管理
存储时候的三个区域:
代码区
存放CPU执行的机器指令(machine instructions)。通常,代码区是可共享的(即另外的执行程序可以调用它),因为对于频繁被执行的程序,只需要在内存中有一份代码即可。代码区通常是只读的,使其只读的原因是防止程序意外地修改它的指令。另外,代码区还规划了局部变量的相关信息。
数据区
该区包含了在程序中明确被初始化的全局变量、静态变量(包括全局静态变量和局部静态变量)和常量数据(如字符串常量)。
未初始化数据区(BSS)
存入的是全局未初始化变量。BSS区的数据在程序开始执行之前被内核初始化为0或者空指针(NULL)。
运行时的几个区域
代码区
代码区指令根据程序设计流程依次执行,对于顺序指令,则只会执行一次(每个进程),如果反复,则需要使用跳转指令,如果进行递归,则需要借助栈来实现。
代码区的指令中包括操作码和要操作的对象(或对象地址引用)。如果是立即数(即具体的数值),将直接包含在代码中;如果是局部数据,将在栈区分配空间,然后引用该数据地址;如果是BSS区和数据区,在代码中同样将引用该数据地址。
全局初始化数据区
同上
未初始化数据区
同上
栈区
由编译器自动分配释放,存放函数的参数值、局部变量的值等。其操作方式类似于数据结构中的栈。每当一个函数被调用,该函数返回地址和一些关于调用的信息,比如某些寄存器的内容,被存储到栈区。然后这个被调用的函数再为它的自动变量和临时变量在栈区上分配空间,这就是C实现函数递归调用的方法。每执行一次递归函数调用,一个新的栈框架就会被使用,这样这个新实例栈里的变量就不会和该函数的另一个实例栈里面的变量混淆。
堆区
用于动态内存分配。堆在内存中位于BSS区和栈区之间。一般 由程序员分配和释放,若程序员不释放,程序结束时有可能由OS回收。
之所以分成这么多个区域,主要基于以下考虑:
一个进程在运行过程中,代码是根据流程依次执行的,只需要访问一次,当然跳转和递归有可能使代码执行多次,而数据一般都需要访问多次,因此单独开辟空间以方便访问和节约空间。
临时数据及需要再次使用的代码在运行时放入栈区中,生命周期短。
全局数据和静态数据有可能在整个程序执行过程中都需要访问,因此单独存储管理。
堆区由用户自由分配,以便管理。
栈与堆的区别:
1、申请方式不同
2、管理方式不同。堆容易产生内存泄露。(这个就看程序员啦)
3、空间大小不同。
栈是向低地址扩展的数据结构,是一块连续的内存区域。这句话的意思是栈顶的地址和栈的最大容量是系统预先规定好的,当申请的空间超过栈的剩余空间时,将提示溢出。因此,用户能从栈获得的空间较小。
堆是向高地址扩展的数据结构(它的生长方向与内存的生长方向相同),是不连续的内存区域。因为系统是用链表来存储空闲内存地址的,且链表的遍历方向是由低地址向高地址。由此可见,堆获得的空间较灵活,也较大。
4、系统响应:
栈:只要栈的空间大于所申请空间,系统将为程序提供内存,否则将报异常提示栈溢出。
堆:操作系统有一个记录空闲内存地址的链表,当系统收到程序的申请时,会遍历该链表,寻找第一个空间大于所申请空间的堆结点,然后将该结点从空闲链表中删除,并将该结点的空间分配给程序,另外,对于大多数系统,会在这块内存空间中的首地址处记录本次分配的大小,这样,代码中的free语句才能正确的释放本内存空间。另外,找到的堆结点的大小不一定正好等于申请的大小,系统会自动的将多余的那部分重新放入空闲链表中。
对于堆来讲,频繁的malloc/free势必会造成内存空间的不连续,从而造成大量的碎片,使程序效率降低。对于栈就不会存在这个问题。
5、增长方向不同
6、申请效率不同
堆的效率要低于栈。
通讯录模型
可以把内存理解为一片广袤的大地,那么, 操作系统就会交给我们一本通讯录,里面有0到$2^{64}-1$ 的地址,每一行地址对应着大地上的某处。我们能拿到的只有地址,但是这个数据具体存在哪里,我们是不清楚也不知道的,只有Kernel才可知道。
多道程序、多线程
https://www.cnblogs.com/liao13160678112/p/6603381.html
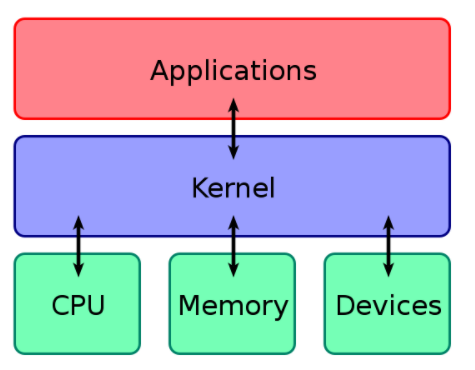
Kernel
kernel是一个软硬件之间的连接器
objdump -d hello
cat cpuinfo 显示cpu信息
cat meminfo 显示内存信息
内存
内存是一个很大的数组空间。
地址空间
地址空间也是一个很大的数组空间,由计算机的字长来决定,比如32位字长机器的内存理论上有4个GB,64位则有$2^{64}$ kb
2.1 信息存储
十六进制表示法
记住十六进制、十进制、二进制的互相转换。记住下面几个表格,主要记牢 十进制的2,4,8,对应的二进制

- 十六进制转换成二进制的时候,可以通过展开每个十六进制的数字来实现。

- 反过来如果给定一个二进制数字,可以通过首先将其从左到右每4位一组来转换为十六进制。如果位总数不是4的倍数,最左边的一组可以少于4位,前面用0补足。然后再将每个4位组转换为相应的十六进制数字
十进制和十六进制之间转换比较简单,使用乘法和除法就可以了。
值得注意的是当值工是2 的非负整数 $n$ 次幂时,也就是$x=2^n$ 我们可以很容易地将x 写成十六进
制形式,只要记住x的二进制表示就是1 后面跟n个0。十六进制数字0 代表4 个二进制 0。所以,当n表示成$i+4j$ 的形式,其中 $0\leq i\leq 3$, 我们可以把x 写成开头的十六进制数字为$1(i=0),2(i=1),4(i=2),8(i=3) $ 后面跟随着个十六进制的0。比如,$x=2048=2^{11}$ 我们有$n=11=3+4*2$ 从而得到十六进制表示 0x800
Data sizes
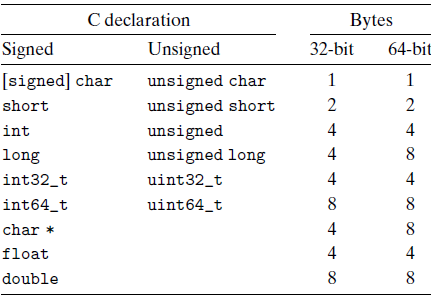
Address and Byte Ordering
Representing Strings
C 语言中字符串被编码为一个以null(其值为0)字符结尾的字符数组。每个字符都由某个标准编码来表示,最常见的是ASCII 字符码。因此,如果我们以参数“12345” 和6(包括终止符)来运行例show_bytes我们得到结果31 32 33 34 35 00。请注意,十进制数字x 的ASCII 码正好是0x3x, 而终止字节的十六进制表示为0x00。在使用ASCII 码作为字符码的任何系统上都将得到相同的结果,与字节顺序和字大小规则无关。因而,文本数据比二进制数据具有更强的平台独立性
下面对show_bytes 的调用将输出什么结果?
1 |
|
要注意,strlen(s) 是不会计算结束符的!所以答案是61, 62,63,64,65
1 | const char *s = "abcdef"; |
Representing Code
考虑下面的C函数
1 | int sum(int x,int y){ |
当我们在机器上编译时,生成如下字节表示的机器代码
1 | Linux 32 55 89 e5 8b 45 Oc 03 45 08 c9 c3 |
我们发现指令编码是不同的。不同的机器类型使用不同的且不兼容的指令和编码方式。即使是完全一样的进程,运行在不同的操作系统上也会有不同的编码规则,因此二进制代码是不兼容的。二进制代码很少能在不同机器和操作系统组合之间移植。
计算机系统的一个基本概念就是,从机器的角度来看,程序仅仅只是字节序列。机器没有关于原始源程序的任何信息,除了可能有些用来帮助调试的辅助表以外。
Boolean Algebra
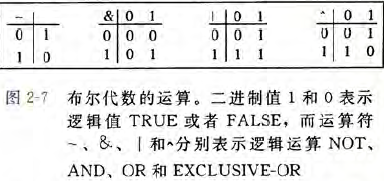
以上4个布尔运算可以扩展到bit vectors上的运算,也就是固定长度为$w$,由0,1组成的串。比如说$w = 4,a =[0110],b=[1100]$ 那么4种运算 $a\&b,a|b,$ a^ b 和 ~b 会得到这样的结果。
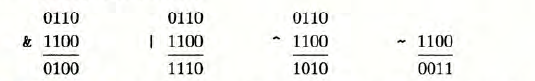
使用bit vectors 一个很有用的应用就是表示有限的集合。我们可以用bit vector $[a_{w-1},\cdots,a_1,a_0]$ 来编码任何子集 $A\subseteq{0,1,\cdots,w-1}$ ,其中$a_i=1$ 当且仅当 $i\in A$ 比如说
$a=[01101001]$ 可以对应 $A={0,3,5,6}$ 因为对76543210 这个数来说,从右往左数第1,第4,第6、7 位都是1,其他位都是0。
同理,$b=[01010101]$ 可以表示 $B={0,2,4,6}$
我们于是可以把位运算用到集合当中:
$A\&B = 01000001 ={0,6}$
$A|B = 01111101 = {0,2,3,4,5,6}$
A^B $= 00111100={2,3,4,5}$
A~B $=10101010={1,3,5,7}$
Bit-Level Operations in C
Logical Operations in C
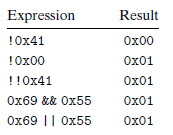
C语言种还提供了一组逻辑运算符 $||,\&\&,!$ 分别对应OR,AND,NOT,千万不要把逻辑运算和位运算混淆,逻辑运算只有TRUE和FALSE,只返回1或者0。比如:
Shift Operations in C 移位运算
左移
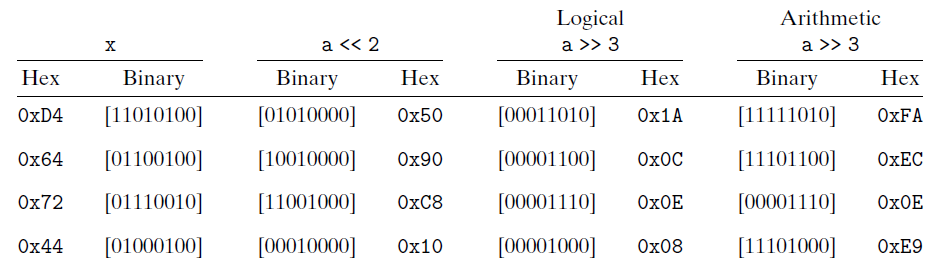
左移这种移位运算非常简单,x向左移动k位,丢弃最高的 $k$ 位,并在右端补上k个0。移位量应该是一个 0~w-1 之间的值。移位运算是从左到右可结合的 $x<<j<<k = (x<<j)<<k$
逻辑右移
逻辑右移和左移刚好相反,x向右移k位,左边补上k个0
算术右移
为什么会有算数右移?
算术右移比较微妙,是在移动之后在左端补上k个最高有效位的值,得到的结果是 $[x{w-1},\cdots,x{w-1},x_{w-2},\cdots,x_k]$
比如下面这个例子

斜体的数字表示的是最右端(左移)或最左端(右移)填充的值。可以看到除了一个条目之外,其他的都包含填充0。唯一的例外是算术右移[10010101]的情况。因为操作数的最高位是1,填充的值就是1。
对于 x<
2.2整数表示
Integral Data Types
Unsigned Encodings(无符号数)
假设有一个整数数据类型有w位。我们可以将其写成 $[x{w-1},x{w-2},…,x_0]$ ,表示向量中的每一位。然乎我们用一个 $B2U_w$(Binary to Unsigned 的缩写,长度位w) 来表示:
对向量 $\overrightarrow{x} = [x{w-1},x{w-2},\cdots,x_0]$
$B2Uw(\overrightarrow{x}) = \Sigma{i=0}^{w-1}x_i2^i$
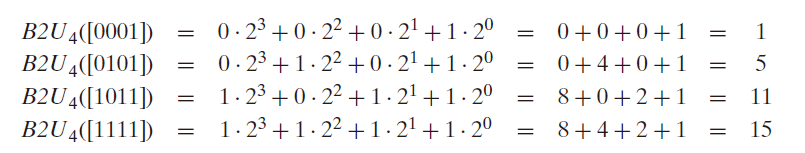
Two’s-Complement Encodings(补码)
基为2的补码的定义
仍然把最高位当成符号位,但是最高位还是带权重的
对向量 $\overrightarrow{x} = [x{w-1},x{w-2},\cdots,x_0]$:
$B2Tw(\overrightarrow{x}) = -x{w-1}2^{w-1}+\Sigma_{i=0}^{w-2}x_i2^i$
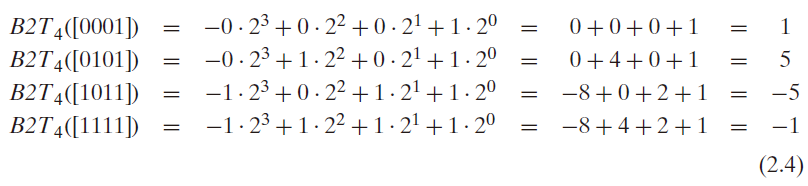
让我们来考虑一下w 位补码所能表示的值的范围。它能表示的最小值是位向量10…0 ,其整数值为 $TMaxw = \Sigma{i=0}^{w-2} 2^i = 2^{w-1}-1$ . 以4为例,我们有 $TMin_4 = B2T_4([1000]) = -2^3 = 8$,而 $TMax_4 = B2T_4([0111]) = 7$
C语言标准不要求一定使用补码表示有符号的整数,但是几乎所有的机器上的实现都用补码
补码的最高位是1,那么这个补码就是负的
补码的好处就是只有一个零,而原码则有两个0
做一个小练习:
B2T (10) = 1010
B2T (−10) = 10110
B2T (15213) =
B2T (−15213) =
我们发现对于两个相反数的补码,我们第一眼是看不出相反数之间是有联系的。不像源码,第一位只代表符号位。对于负数的补码,就是把正数的补码取反码再+1
Conversions between Signed and Unsigned
有符号数和无符号数之间的转换。
1 | short int v = -12345; |
结果是 v=-12345, uv = 53191
对C来说强制类型转换的结果保持位值不变,只是改变了解释这些位的方式。 因为十六进制表示写作0xCFC7 的16 位二进制码既是-12345的补码表示,又是53191 的无符号表示
也就是说 $T2U_{16}(-12345) = 53191,U2T_16(53191) = 12345$
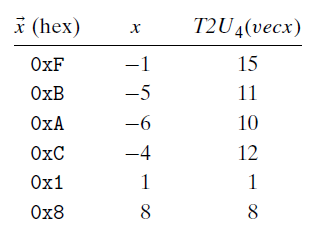
通过上述这些例子,我们可以总结出T2U的公式:对满足 $TMin_w\leq x\leq TMax_w$
$T2U_w(x)=\begin{cases}x+2^w,x<0\ x,x\geq 0\end{cases}$
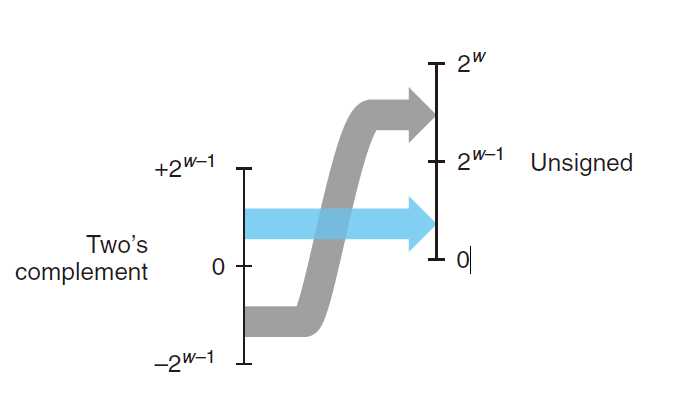
对 $0\leq u\leq UMax_x$ 的u 有
$U2T_w(x)=\begin{cases}u,u\leq TMax_w\ u-2^w,u\geq TMax_w\end{cases}$
Signed versus Unsigned in C
C语言中,要创建一个无符号常量,必须加上后缀字符’U‘ 或者‘u‘例如,12345U 或者0x1A2Bu.
C 语言允许无符号数和有符号数之间的转换。在一台采用补码的机器上,当从无符号数转换为有符号数时,效果就是应用函数$U2T_w$,而从有符号数转换为无符号数时,就是应用函数$T2U_w$ 其中切表示数据类型的位数。
| Constant1 | Constant2 | ||
|---|---|---|---|
位串保持不变,位串重复解读。可能会导致各种溢出:$$
Expanding the Bit Representation of a Number
零扩展
要将一个无符号的数转换为一个更大的数据类型,我们只需要简单地在表示的开头添加0. 表示:
定义宽度为w的位向量 $\overrightarrow{u} = [u{w-1},u{w-2},…,u0]$ 和宽度为 $w’$ 的位向量 $\overrightarrow{u}’ = [0,…,0,u{w-1},u{w-2},…,u_0]$ , 其中 $w’>w$, 则 $B2U_w(\overrightarrow{u}) =B2U{w’}(\overrightarrow{u’})$
符号扩展
要将一个补码数字转换成一个更大的数据类型,可以执行一个符号扩展,在表示中添加最高有效位的值。表示为如下原理。
定义宽度为 w的位向量 $\overrightarrow{x} = [x{w-1},x{w-2},…,x0]$ 和宽度为 w的位向量 $\overrightarrow{x}’ = [x{w-1},…,x{w-1},x{w-1},x{w-2},…,x_0]$ ,其中 $w’>w$ 。 则 $B2T_w(\overrightarrow{x}) =B2T{w’}(\overrightarrow{x’})$
比如下面这个例子
1 | short sx = -12345; /* -12345 */ |
打印如下:
sx = -12345: cf c7
usx = 53191: cf c7
x = -12345: ff ff cf c7
ux = 53191: 00 00 cf c7
我们可以观察到,-12345的补码和53191的无符号表示在16位字长时是相同的,但是在32位字长时却不同的。因为前者用的是符号扩展,后者用的是零扩展
Truncating Numbers
刚才我们讲了怎么从位数较少的拓展成位数较多的数,现在来看看高位数怎么截断成较少位数
当我们将一个w位的数$ \overrightarrow{x} = [x{w-1},x{w-2},\cdots,x0]$ 截断位一个k位数字时,我们会丢弃高 $w-k$ 位,得到一个位向量 $\overrightarrow{x’} =[x{k-1},x_{k-2},\cdots,x_0]$ 阶段一个数字很可能会改变它的值。
截断无符号数
对一个无符号数,我们可以很容易得出其数值结果
令$\overrightarrow{x} $ 等于位向量 $ \overrightarrow{x} = [x{w-1},x{w-2},\cdots,x0]$ ,而 $\overrightarrow{x’}$ 是将其截断为k位的结果:$\overrightarrow{x’} =[x{k-1},x_{k-2},\cdots,x_0]$ 。 令 $x=B2U_w(\overrightarrow {x}),x’ = B2U_k(\overrightarrow{x’})$ 则 $x’ = x mod 2^k$
截断补码数值
截断补码也具有相似的属性,只不过要将最高位转换为符号位。
令 $\overrightarrow{x}$ 等于位向量 $[x{w-1},x{w-2},\cdots,x0]$ ,而 $\overrightarrow{x’} $ 是将其截断为k位的结果: $\overrightarrow{x’} =[x{k-1},x_{k-2},…,x_0]$ 令 $x=B2U_w(\overrightarrow{x})$, $x’ = B2T_k(\overrightarrow{x’})$ 则 $x’ = U2T_k(x mod 2^k)$
在这个公式中, $x ~~ mod ~~2^k$ 将是一个 0 到 $2^k-1$ 之间的一个数。对其应用函数 $U2Tk$ 产生的效果就是把最高的有效位 $x{k-1}$ 的权重从 $2^{k-1}$ 转变为 $-2^{k-1}$ 。 举例来看,将数值 $x=53191$ 从int 转换为short。 由于 $2^{16} =66536 \geq x$ 我们有 $x ~~ mod ~~ 2^{16} =x$ 但是,当我们把这个数转换为16位的补码时,我们得到了 $x’ = 53191-65536 = -12345$
扩展和截断小结
扩展:
⽆符号:加 0
有符号:最⾼位扩展
结果可靠(可预期)
截断:
⽆论有⽆符号:去掉⾼位,结果重新解释
⽆符号:等同于取模运算
有符号:类似于取模运算(先取模再重新解释)
对于不太⼤的数,结果可靠(可预期)
Advice on Signed versus Unsigned
就像我们看到的那样,有符号数到无符号数的隐式强制类型转换导致了某些非直观的行为。而这些非直观的特性经常导致程序错误,并且这种包含隐式强制类型转换的细微差别的错误很难被发现。因为这种强制类型转换是在代码中没有明确指示的情况下发生的,程序员经常忽视了它的影响。
下面两个练习题说明了某些由于隐式强制类型转换和无符号数据类型造成的细微的错误
1 | /* WARNING: This is buggy code */ |
当参数length 等于0 时,运行这段代码应该返回0.0。 但实际上,运行时会遇到一个内存错误。请解释为什么会发生这样的情况,并且说明如何修改代码.
因为length是unsigned 的,那么0-1 就会变成了Umax也就是4294967295,但是 $<=$ 这个符号同样使用无符号数比较,而因为任何书都是小于等于UMax的,所以这个比较总是为真。因此代码将试图访问数组a的非法元素。
我们可以将length修改为int类型
1 | /* Prototype for library function strlen */ |
当你在一些示例数据上测试这个函数时,一切似乎都是正确的。进一步研究发现在头文件stdio.h 中数据类型size_t 是定义成unsigned int 的。并解释为什么会出现这样不正确的结果。
当s比t更短的时候,因为strlen(s)和strlen(t) 都是unsigned的,所以不会出现负数而是一个很大的正数,任然会返回1
C. 说明如何修改这段代码好让它能可靠地工作 将代码修改为:return strlen(s) > strlen(t);
解题要点:
Unsigned和补码之间的比较
如果左边的数是Unsigned,那么右边的数也会自动转换成Unsigned(最后一题有点坑)
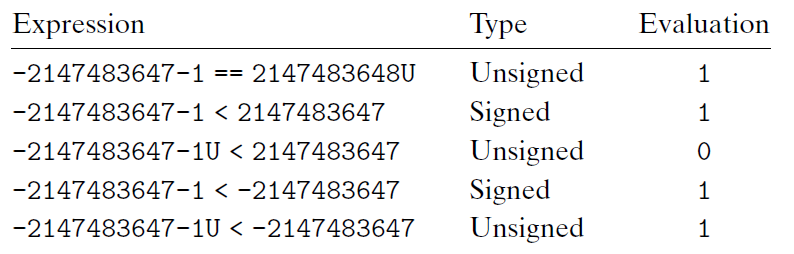
最后一题,-2147483647-1U 会变成0,同时右边的-2147483647 会转换成1,0<1 所以正确

对于fun1 来说,是unsigned类型移位之后再转换为int,所以进行的操作是左移或者逻辑右移
对于fun2 来说,左移后先转换成int再进行算术右移。
所以fun1就是不用变化,而对于fun2,我们要看哪些数在左移后以1开头,我们发现是0xC9000000 和 0x87000000,那么算数右移后,fun2(w) = 0xFFFFFFC9 和 0xFFFFFF87