CSAPP信息的表示和存储2

整数运算

无符号加法

当两个非负整数 x,y 满足 $0\leq x,y< 2^w$ 。那么 $x+y$ 就有可能是一个w+1位数。比如一个四位的无符号整数的取值范围是0-15，但其和的范围是0~30. 我们要让无符号数之和仍然位w位，那么我们需要做数的截断。

我们定义 一个运算 $+_w^u$ ，其操作是把整数 x+y 截断为w位得到的结果，再把这个结果看作是一个无符号数。这可以被视为一种形式的模运算，对 $x+y$ 的位级表示，简单丢弃任何权重大于 $2^{w-1}$ 的位就可以了。比如考虑一个4位数字表示， $x=9$ 和 $y = 12$ 的位表示分别是 $[1001]$ 和 $[1100]$ 。他们的和是21，5位表示为$[10101]$ 但是如果丢弃最高位，我们就得到了 $[0101]$ 也就是说 十进制的值是5，这和21 mod 16 = 5 一致。

我们可以将操作 $+_w^u$ 这样描述

对满足 $0\leq x,y< 2^w$ 的 x和y有：

$x+_w^u y =\begin{cases}x+y,x+y\leq 2^w ~~ 正常\ x+y-2^w,2^w\leq x+y<2^{w+1}~~ 溢出\end{cases} $

如下图，左边的 x+y y映射到右边的无符号 w位的和 $x~+_w^u ~y$ 正常情况下 x+y 的值保持不变，而溢出的情况则是该和减去$2^w$ 后的结果。

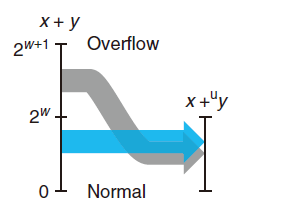
当执行 C程序时，不会将溢出作为错误而发信号。不过有的时候，我们可能希望判定是否发生了溢出

对在范围 $0\leq x,y\leq UMax_w $ 中的x和y， 令 $s=x~+_w^u ~y$ 。则对计算 s，当且仅当 $s<x$ 时，发生了溢出。

比如说，在前面的示例中，我们看到 $9~+_4^u~12 = 5$. 由于 $5<9$ ,我们可以看出发生了溢出。

补码加法

对于补码加法，我们必须确定当结果太大或者太小时，应该做些什么

给定在范围 $-2^{w-1}\leq x,y\leq 2^{w-1}-1$ 之内的整数值x和y，它们的和就在 $-2^w\leq x+y\leq2^w-2$ ，要想准确表示，可能需要w+1 位。我们把他截成w位，并将这个结果看做是补码数。

对满足 $-2^{w-1}\leq x,y\leq 2^{w-1}-1$ 的整数x和y，有：

$x+_w^t~y = \begin{cases}x+y-2^w,2^{w-1}\leq x+y 正溢出\ x+y,-2^{w-1}\leq x+y<2^{w-1}正常\x+y+2^w,x+y<-2^{w-1} ~~ 负溢出\end{cases}$

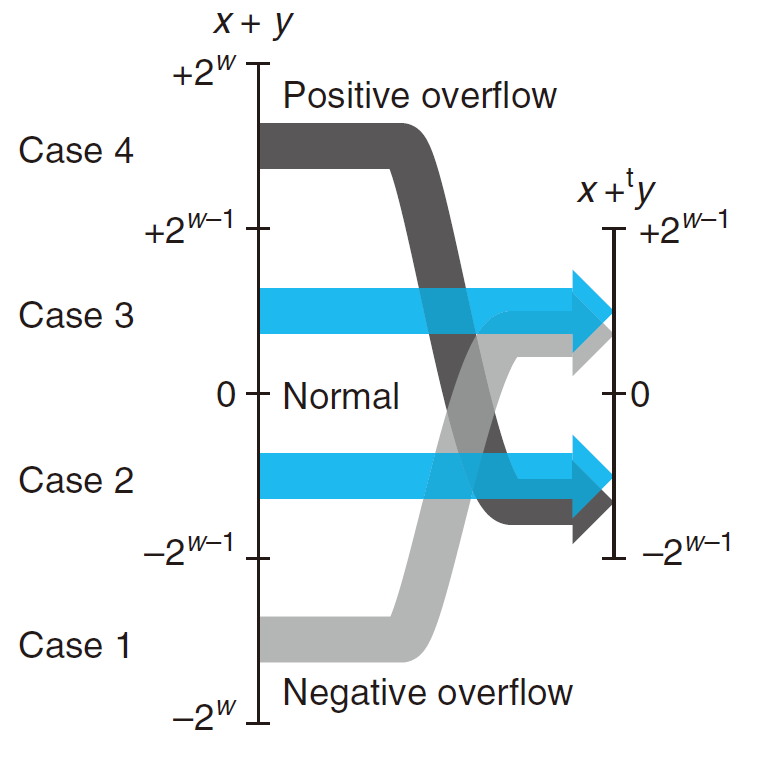
两个数的w 位补码之和与无符号之和有完全相同的位级表示。实际上，大多数计算机使用同样的机器指令来执行无符号或者有符号加法。

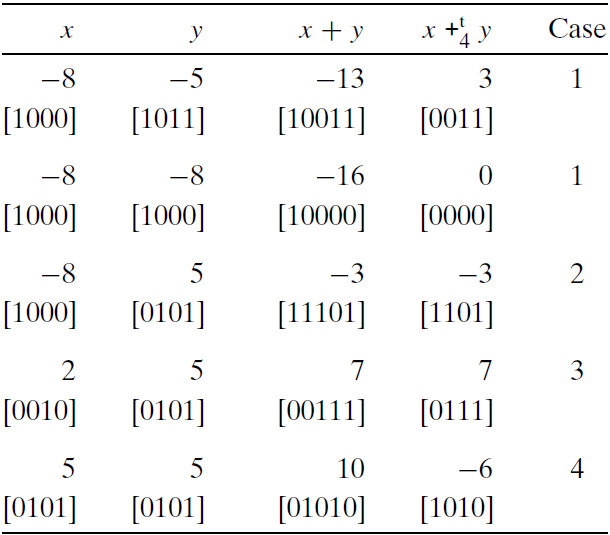
上图阐述了字长 $w=4$ 的补码加法。运算数的范围为 $-8到7$ 之间 。当$x+y<-8$ 时，补码加法就会负溢出，导致和增长了16(Case 1)。当 当 $-8\leq x+y <8$ 时，加法就产生了 $x+y$ 。当 $x+y\geq 8$ ,加法就会正溢出，让和减少了16。

检测补码加法中的溢出

对满足 $TMin_w\leq x,y\leq TMax_w$ 的x和y，令 $s=x~+_w^t~y$ . 当且仅当 $x>0,y>0$ 但是 $s\leq0$ 时，计算s发生了正溢出。当且仅当 $x<0,y<0$但是 $s\geq 0$ 时，计算s发生了负溢出。

位操作相同的好处

这样会让电路逻辑变得更简单，电路在设计的时候并不需要判断是否为补码或者无符号数。

无符号的非

我们可以定义一个加法逆元(减) $-_w^u$ 。满足 $-_w^ux+_w^ux=0$

无符号数求反

$-_w^u x=\begin{cases}x,x=0\ 2^w-x,x>0\end{cases}$

补码的非

可以看到范围在 $TMin_w\leq x\leq TMax_w$ 中的每个数字x都有 $+^t_w$ 下的加法逆元，我们把 $-_w^t x$ 表示如下：

补码的非

对满足 $TMin_w\leq x\leq TMax_w$ 的x，其补码的非 $-^t_w x$ 可表示为

$-_w^t x=\begin{cases}TMin_w,x=TMin_w\ -x,x>TMin_W\end{cases}$

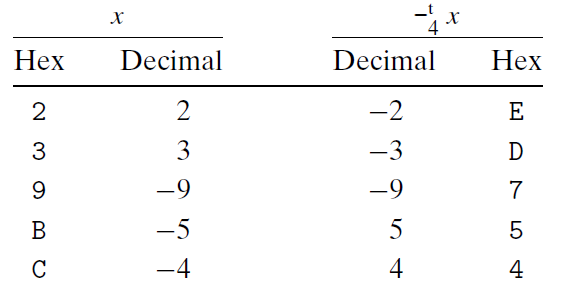
补码的非和无符号的非拥有相同的模式

无符号乘法

范围在 $0\leq x,y\leq 2^w-1$ 内的整数 x和y 可以被表示为 w位的无符号数，但是它们的乘积 $x\cdot y$ 的取值范围是 $(2^w-1)^2 = 2^{2w}-2^{w+1}+1$ 之间。这可能需要2w位来表示。不过C愿意浓重的无符号乘法被定义为产生w位的值。因此我们需要进行数的截断，我们将这个值表示为 $x *_w^u y$

将一个无符号数截断位w位等价于计算值mod $2^w$ 得到：

对满足 $0\leq x,y\leq UMax_w$ 的x和y 有：

$x *_w^u y = (x\cdot y)mod 2^w$

补码乘法

和无符号乘法类似， 范围在 $-2^{w-1}\leq x,y\leq 2^{w-1}-1$ 内的整数x和y可以被表示为位的补码数字，但是它们的乘积$x\cdot y$ 取值在 $-2^{2w-2}+2^{w-1}$ 到 $2^{2w-2}$ 之间，于是我们需要把这个可能长度位2w的串截断成w位的串。我们将这个数值表示为 $x*_w^t y$ 。将一个补码数截断为w位相当于先计算值模 $2^w$ 再把无符号数转换为补码，得到：

对满足 $TMin_w\leq x,y\leq TMax_w$ 的x和y有：

$x*_w^t y = U2T_w((x\cdot y) mod 2^w)$

所以对无符号和补码乘法来说，乘法运算的位级表示都是一样的，只是解释的方法不同而已。比如下面这个例子，我们就可以看到截断过后补码乘法和无符号乘法的编码都是相等的。

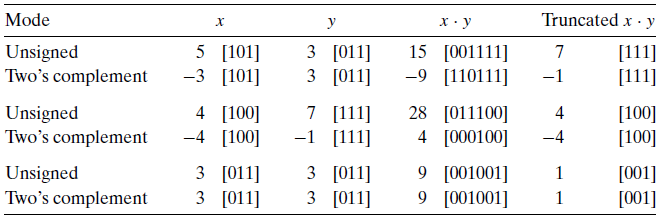
如果乘法需要保留未被阉割的结果，需要扩展字长。如果需要，由软件(库)实现。

例子：11101001*11010101

乘以常数

我们的编译器对整数乘法指令进行了一定的优化，试着用移位或者加法运算的组合来代替乘以常数因子的乘法。首先我们会考虑乘以2的幂的情况，然后再概括成乘以任意常数。

设x为位模式$[x{w-1},x{w-2},\cdots,x0]$ 表示的无符号整数。那么对任何 $k\geq 0$ 我们都热为$[x{w-1},x_{w-2},\cdots,x_0,0,\cdots,0]$ 给出了 $x2^k$ 的 $w+k$ 位的无符号表示，也就是右边加上了k个0

比如，当 $w=4$ 时， 11可以表示为 $[1011]$ 。$k=2$ 时将其左移得到6位向量[101100] ，即可编码为无符号数11*4 =44

那么我们可以固定字长，再左移k为时，相当于其最高的k位被丢弃。得到
$[x{w-k-1},x{w-k-2},\cdots,x_0,0,\cdots ,0]$ 而执行固定字长的乘法，也是这种情况，因此我么可以看出左移一个数值等价于执行一个于2的幂相乘的无符号乘法。

其实，在C里面就是通过移位来计算无符号乘法和补码乘法的

C变量x和k有无符号数值x和k，且 $0\leq k\leq w$ ,则C表达式 $x<<k$ 产生数值 $x_w^u 2^k$ . 类似的，补码乘法也可以由此定义 ，只是将 $x<<k$ 产生的数值改变为 $x_w^t2^k$

注意，无论时无符号运算还是补码运算，乘以2的幂都有可能导致溢出。但是即使溢出时我们通过移位导致的运算结果也是一样的。比如说[1011]左移两位得到[101100] 这显然溢出了，我们将这个值截断位4位得到[1100] 也就是44 mod $2^4$ = 16

由于整数乘法比移位和加法的代价要大得多，许多C 语言编译器试图以移位、加法和减法的组合来消除很多整数乘以常数的情况

比如对于整数 4[100] 和7[111] 计算4*7 可以化为 $4*(2^2+2^1+2^0)$ ，也就是变成了 $[10000]+[01000]+[00100] = [11100] = 2^4+2^3+2^2=28$

再将$[11100]$截断为4位也就是 $[1100]$ ,也就是28mod 16 = 12

当然有时候还可以变成减法，比如乘以14可以变为 $2^4-2^1$ ,将其重写为$(x<<4)-(x<<1)$

当然，选择使用移位、加法和减法的组合，还是使用一条乘法指令，取决于这些指令的相对速度，而这些是与机器高度相关的。大多数编译器只在需要少量移位、加法和减法就足够的时候才使用这种优化

除以2的幂

除以2的幂的无符号除法

无符号数

有无符号数值x和k，且 $0\leq k>k 产生数值 ⌊$x/2^k$⌋
对无符号来说，右移采用的是逻辑右移。下面是一些无符号右移的例子：

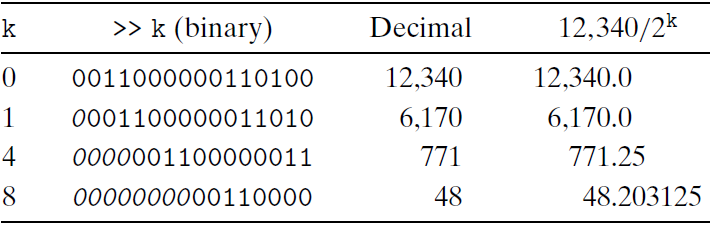
对于无符号来说，右移和除法是等价的。都是向下取整

有符号数(补码)

C语言中有补码值x和无符号数值k，且 $0\leq k>k$ 产生数值 ⌊$x/2^k$⌋

对于 $x\geq 0$ 变量 x的最高有效位为0，所以效果与逻辑右移是一样的。因此对于非负数来说，算数右移k位与除以 $2^k$ 是一样的。

对于 $x<0$ ，情况要复杂一点，首先为了保证负数仍然为负，我们要执行的是算术右移。c表达式 x>>k产生的数值为$[x/2^k]$

但是当补码除以$2^k$ 的时候，运行的是 $(x+(1<>k$ ，这个是向上取整的。

关于这个公式。我们可以分几种情况来讨论。首先$1<<k -1 == 2^k-1$ 也就是 $\overline {1\cdots 1}$

如果可以整除$2^k$ 说明二进制右边k位都为0，这样加上 $\overline {1\cdots 1}$ 之后再右移k位相当于把 $\overline {1\cdots 1}$ 都移走了。

如果不能整除$2^k$ 那么对于无符号数，$(x+(1<>k$ 是向上取整的。对于有符号数的负数，$(x+(1<>k$ 是向上取整的。有符号数的正数部分不要用这个公式。

	无符号数	补码的正数	补码的负数
除以$2^k$	向下取整(向0取整)	向下取整(向0取整)	$(x+(1<>k$ 向上(0)取整
右移k位	向下取整，逻辑右移	向下取整(算数右移)	向下取整(算术右移)

那么我们也可以从中推导出向0取整的位运算。$(x<0~~?~~x+(1<> k$

补码的相反数

$-x == $ ~$x +1$

什么时候应该用无符号数

• Do Use When Performing Modular Arithmetic

  • Multiprecision arithmetic
• Do Use When Using Bits to Represent Sets
  • Logical right shift, no sign extension
• Do Use In System Programming
  • Bit masks, device commands,…

浮点数

这章我们将看到 IEEE浮点格式中数字是如何表示的，我们还将探讨舍入的问题，即向上调整或者向下调整。

二进制小数

理解浮点数的第一步是考虑含有小数值的二进制数字.

首先我们来理解十进制下的小数，$dmd{m-1}\cdots d1d_0d{-1}d{-2}\cdots d{-n}$ ，那么 $d=\Sigma_{i=-n}^m 10^i * d_i$

比如12.34就相当于 $110^1+210^0+310^{-1}+410^{-2} = 12\frac{34}{100}$

我们类比一下，二进制的浮点数就可以写为 $bmb{m-1}\cdots b1b_0b{-1}b{-2}\cdots b{-n}$ 的表示法，其中每个二进制数字，或者称为位，$b_i$ 的取值范围是0和1，如

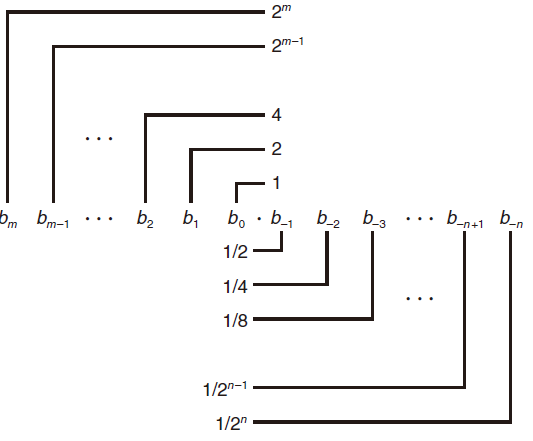
用这种方式定义的二进制如下： $b=\Sigma_{i=-n}^m 2^i b$ 比如说 $101.11_2$ 可以表示为数字 $12^2+02^1+12^0+12^{-1}+12^{-2}= 4+0+1+\frac{1}{2}+\frac{1}{4} = 4\frac{3}{4}$

从等式中可以很容易地看出来，二进制小数点向左移一位相当于这个数被2除。例如，$101.11_2$ 表示数 $5\frac{3}{4}$ 而 $10.111_2$ 表示数 $2+0+\frac{1}{2}+\frac{1}{4}+\frac{1}{8} = 2\frac{7}{8}$ 类似，二进制小数点向右移动一位相当于将该数乘2，比如 $1011.1_2$ 可以表示数 $8+0+2+1=11\frac{1}{2}$

注意，形如$0.11⋯1_2$的数表示的是刚好小于1 的数。例如，$0.111111_2$ 表示$\frac{63}{64}$ ，将用简单的表达法$1.0-\epsilon$ 来表示这样的数值。

假定我们仅考虑有限长度的编码，那么10进制表示法不能准确地表达像$\frac{1}{3}$和$\frac{5}{7}$ 这样的数。类似，小数的二进制表示法只能表示那些只能够被写成 $x*2^y$ 的数，其他的值只能被近似的表示。

比如说 $\frac{1}{3} = 0.0101010101[01]_2$

比如说，数字 $\frac{1}{5}$ 可以用十进制小数 $0.20$ 精确表示。不过，我们并不能把它准确的表示为一个二进制小数，我们只能近似表示它，增加二进制表示的长度可以提高表示的精度。

IEEE浮点表示

IEEE 浮点标准，使用 V(浮点数) = $(-1)^s\times M\times 2^E$ 的形式来表示一个数。这就是一个二进制科学计数法的表示形式。

s代表sign， 是决定这个数是负数(s=1) 还是正数(s=0) ,而对于数值0的符号位解释作为特殊情况处理。

M代表尾数(significand) M是一个二进制的小数，范围要么在 $(1,2-\epsilon)$ 之间要么在 $(0,1-\epsilon)$ 之间

E代表阶码(exponent) E的作用是对浮点数加权，这个权重 就是二的E次幂(可能是负数)

如下图所示

在单精度浮点数(float) 中，s,exp,frac 字段分别为 1 位，$k=8$ 位和 $n=23$ 位

在双精度浮点数(double) 中，s、exp、frac 字段分别为1位，$k=11$ 和 $n=52$ 位，得到一个64位的表示。

将浮点数的这三个字段分别编码：

• 一个单独的符号位 s 直接编码符号 s
• k位的阶码字段 $exp = e_{k-1}\cdots e_1e_0$ 编码阶码E。
• n位小数字段$frac= f_{n-1}\cdots f_1f_0$ 编码尾数M，但是编码出来的值也依赖于阶码的字段是否等于0。

为什么exp再frac前面？当我们对两个同符号数比较大小的时候，可以先直接比较阶的大小。但是尾数在前面的话就会增大计算量。

根据 exp 的值，被编码的值可以分成三种不同的情况(最后一种情况有两个变种)

1.Normalized

这是最普遍的情况。即当exp的位模式既不全为0(数值0) ,也不全为1(单精度数值为1，双精度数值为2047) 时，都属于这类情况，在这类情况中，阶码字段被解释为以偏置(biased)的形式表示的有符号整数。也就是说，阶码的值是 $E=e-Bias$, 其中e是无符号数，其为表示为 $e_{k-1}\cdots e_1e_0$ ,而$Bias$ 是一个等于 $2^{k-1}-1$(单精度是127, 双精度 1023) 的定值，目的是让原来都是正的指数一部分变成负的。由此产生指数的取值范围，对单精度是 $-126$~$+127$ ,而对于双精度来说是 $-1022到 +1023$

那么问题来了，为什么我们不用补码去表示，而要用 e-Bias 这种移码来表示呢？ 因为对于阶来说，主要是用来比较大小和加减法，从这个角度看，虽然表示的范围相近，但是移码的计算更加方便。

小数字段frac 被解释为描述小数值f , 其中 $0\leq f<1$ ，其二进制表示为 $0.f_{n-1}\cdots f_1f_0$ ,也就是二进制小数点在最高有效位的左边。尾数定义为 $M=1+f=1.frac$ 。

这个设计难懂但是非常巧妙。这个方法有时也被叫做隐含的以1 开头的(implied leading 1)表示 。也就是说我们可以把 M看作是一个二进制表达式 $1.f{n-1}f{n-2}\cdots f_0$ 的数字。既然我们总是能够调整阶码E，使得尾数M在范围 $1\leq M<2$ 之中(假设没有溢出)。那么这种表示方法就可以轻松获得一个额外精度位的技巧。既然第一位总是等于1，那么我们就不需要显示地表示。

比如说对于一个浮点数 f=.10101,如果我们不把小数点左边的数值设置为1，让$exp(2^k)$ 来操纵小数点移位，那么表示.10101 就需要5位。但是我们如果把小数点左边的数值设置为1，那么再让$exp(2^k)$ 来操纵小数点移位后，表示.10101 只需要用 1.0101 表示后再像右移一位就行了，也就是说我们现在只需要4位就可以编码出 .10101. 相当于牺牲了阶码中的1，但获得一个精度位,能多表示 $2^{127}$ 个数。

2.Denormalized

仅仅Normalized浮点数时不够的，因为Normalized能表示的绝对值最小的浮点数和绝对值次小值浮点数之间的差距是要小于绝对值最小的浮点数和0之间的差距的。这和科学计数法的“本意”相违背。科学计数法要求越接近0.数值越密，但是对Normalized来说，到0之间存在一段比较大的“真空”值。

从下面这张表格我们可以更明显地看出Normalized局限性。在8位浮点数种， 阶码位k=4,小数位 n=3,偏置量 $2^{3}-1 =7$ .那么这个8位浮点数能表示的最小的Normalized数就是 0.0001000，f=0 但是$ M = 1+f =\frac{8}{8}$ $V_1 = 2^E\times M = 2^{-6}\times 1=\frac{1}{64}$ = 0.015625
Normalized的次小值是 $0.0001001$ ，值$V_2=0.017578$

$V_2-V_1<V_1-0.0$ ，就不符合科学计数法的主旨。

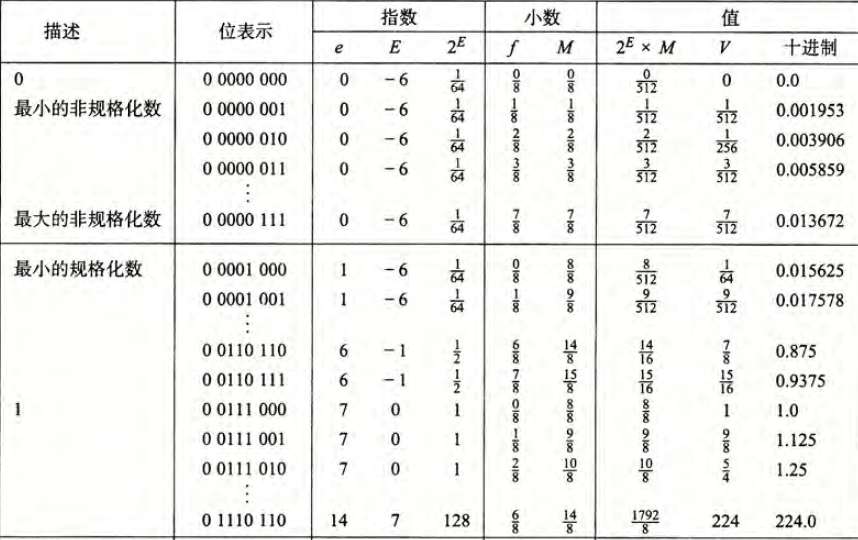
所以我们设计了Denormalized数，也就是阶码域为全0。这种情况下，阶码的值 是$E=1-Bias$ 。而尾数的值是 $M=f$，也就是小数字段的值，小数点左边为0。Denormalized能够提供一个逼近于0的数，也就是讲上面所说的那段真空区域等分。

为什么将阶码的值设为 $E = 1-Bias$？把$M=f $这样设计可以让最大的Denormalized和最小的Normalized能够平顺连接.我们知道在8位的浮点数下，最小的 Normalized 数为0.015625，而最大的Denormalized 为0.013672 ，他们之间相差了 $\frac{1}{512}$ 。从最大的Deormalized数继续向0逼近，所有的数之间都是等间距的，因为阶数始终为0。

非规格化数有两个用途。

首先，这提供了一种表示数值0的方法，因为使用规格化数，我们必须总是使 $M\geq 1$ ，因此我们不能表示0，实际上，$+0.0$ 的浮点表示的位模式为全0：符号位是0，阶码字段全为0(表明一个非格式化的值) ，而小数域也全为0，这就得到了 $M=f=0$ 令人奇怪的是，当符号位为1，而其他域全为0的时候，我们得到了值 $-0.0$。 +0和-0 其实表示了是从正向还是负向无限接近于0。

非格式化数的另外外一个功能是表示那些非常接近于0.0的数

3.1Infinity

最后一类数值是当 阶码全为1的时候出现的。当小数域全为0时，得到的值表示无穷。当s=0 时是$+\infty$ ，或者当 $s=1$ 时是 $-\infty$ 。当我们把两个非常大的数相乘，或者除以0时，无穷能表示溢出的结果

比如说 1.0/0.0可能会取到Infinity，这是因为 0.0可能不是真正的0，只是相近为0，所以1.0/0.0 可能是有意义的。

3.2NaN

但是当小数域不为0的时候，结果值被称为 NaN，即(Not a Number)，一些运算的结果不能是实数或者无穷，就会返回这样的NaN值，比如当计算 $\sqrt{-1}$ 或 $\infty - \infty$ 的时。在某些应用中，表示未初始化的数据时，他们也很有用处。

数字示例

现在我们假设一个6位的浮点数，有 $k=3$ 的阶码位和 $n =2$ 的尾数位。偏置量是 $2^2-1=3$ 。那么下面的图就显示了所有可表示的值(除了NaN) 。两个无穷值在两个末端。最大数量值的Normalized数是 $\pm14$ Denormalized数聚集在 0 附近。

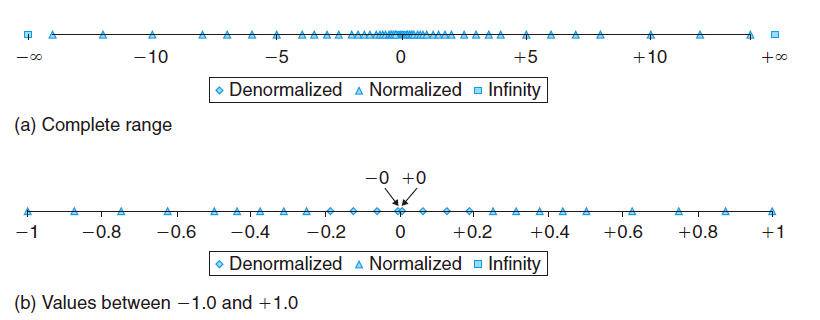
我们发现, 那些可以表示的数并不是均匀分布的：越靠近原点处它们越稠密。

舍入

因为表示的方法限制了浮点数的范围和精度，所以浮点运算只能近似地表示实数运算。因此对于值x，我们一般通过舍入运算来找到最接近的匹配值 x’, 那么我们就不能选择四舍五入。因为这样向上舍入的概率会大于向下舍入的概率。下面是四种不同的摄入方式，第一种是向偶数舍入，也就是说，出现 x.5 的时候，向这个数的最接近的偶数舍入。比如 1.5向2舍入；2.5向2舍入 -2.5向-2 舍入。这样一来，向上舍入和向下舍入的概率就相等了。单仅限于最后一位是5，其他的数字还是按照四舍六入的方式进行。

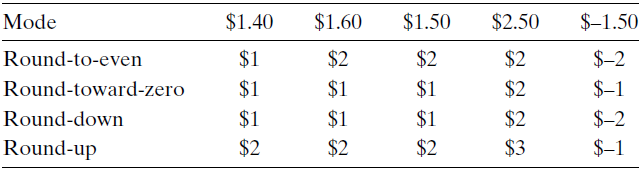
那么，对于二进制小数，我们也可以使用向偶数舍入。我们将最低有效位的值0 认为是偶数，值1认为是奇数。那么只有对形如 $X\cdots X.Y\cdots Y100\cdots$ 的二进制位模式的数才可以向偶数舍入。最右边的Y是要被舍入的位置。如果最后是100的话，就要把Y向偶数舍入，Y若为1，那么向上舍入取0进1，若Y为0，那么直接移去后面的100.

比如 $10.11100 $向上舍入成11.00，而10.10100 向下舍入成10.10

像其他的数，如 $10.00011_2$ 就直接向下舍入到 $10.00$ 而 $10.00110_2$ 向上舍入到 $10.01_2$

浮点运算

$x +_f y = Round(x + y)$
$x ×_f y = Round(x × y)$

浮点数的加法或者乘法可能会溢出，也可能需要舍入。

乘法

对于两个浮点数 $(-1)^s\times M\times 2^E$ 相乘得到 $=(-1)^{s_1}\times M_1\times 2^{E_1}\times(-1)^{s_2}\times M_2\times 2^{E_2}$

所以结果就可以这样表示：$s = s_1$^$s_2,M=M_1\times M_2,E=E_1+E_2$

那么，如果 出现了 $M\geq 2$ ，则M右移，增加E

如果E超过了范围，那么就发生了溢出

如果E不超过范围，那么对M进行舍入，计算得到frac

乘法的数学性质：

• 封闭
• 交换律成立
• 结合律不成立
• 1的性质成立
• 乘法对加法的分配律不成立
• 单调性成立 $(a\geq b ~\&~c\geq 0\Rightarrow ac\geq bc)$ (除了$\infty$和$NaN$)

加法

结果$(-1)^s\times M\times 2^E=(-1)^{s_1}\times M_1\times 2^{E_1}+(-1)^{s_2}\times M_2\times 2^{E_2}$

对于 s,M: 小数点对齐之后做加法

E则取 对齐后的 $E_1$

• 如果 $M\geq 2$ 则M右移，增加E
• 如果E超过范围，则溢出
• 如果E没超出范围，则M舍入，计算得到frac

如果两个浮点数的阶数E不同，那么需要先移动小数点调整他们的阶相同之后再进行

加法的数学性质：

• 封闭(包括NaN)
• 交换律成立
• 结合律不成立
• 0的性质成立
• 相反数存在(除了$\infty$和$NaN$)
• 单调性成立(除了$\infty$和$NaN$)

C语言中的浮点数

所有的C语言版本提供了两种不同的浮点数据类型：float 和double。 在支持IEEE 浮点格式的机器上，这些数据类型就对应于单精度和双精度浮点。另外，这类机器使用向偶数舍入的舍入方式。不幸的是，因为C语言标准不要求机器使用IEEE 浮点，所以没有标准的方法来改变舍人方式或者得到诸如$-0,+\infty,-\infty$ 或者 $NaN$ 之类的特殊值。大多数系统提供include(‘.h’) 文件和读取这些特征的过程库，但是细节随系统不同而不同。例如，当程序文件中出现下列句子时，GNU 编译器GCC 会定义程序常数 INFINITY($+\infty$) 和 $NaN$(表示$NaN$)

#define _GNU_SOURCE 1
#include <math.h>

作业

int add_ok(unsigned x,unsigned y){
	return x+y>=x;
}

int tadd_ok(int x,int y){
	int sum = x+y;
	int neg_over = x<0&&y<0&&x+y>=0;
	int pos_over = x>=0&&y>=0&&x+y<0;
	return ~(neg_over||pos_over);
}

不管是否溢出，加减法仍然成立

因为float只有32位，和int是一样的，8位阶码 ，23位尾数；而double有64位，11位阶码，52位尾数

double的尾数用来容纳int是绰绰有余的，而float的尾数则需要int舍弃一些精确度。于是A是正确的而B是错误的