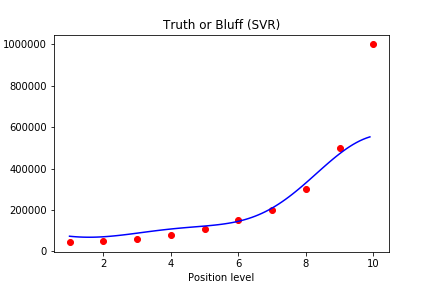
支持向量回归（SVR）

Posted on
Words count in article: 2.3k | Reading time ≈ 8

支持向量回归（SVR）

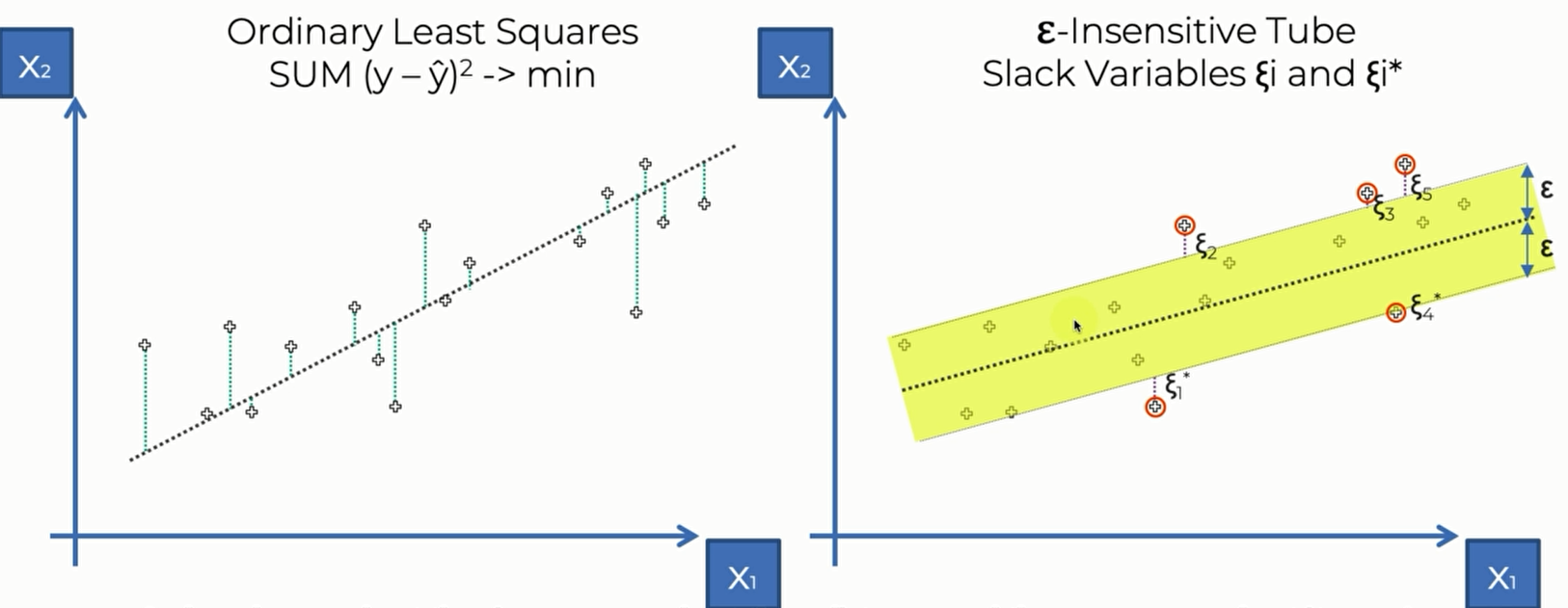
左图是Linear Regression的 ,右边是svr 的loss function，右图中，$\epsilon-$ Insensitive tube描述的是黄色管道，$\epsilon$ 是管道边界到管道中心的垂直距离。我们定义这个区域内的点损失为0，这个区域以外的点的损失是点到区域边界的距离，这些区域外的点（或者有可能边界上的点）就是svr 的support vector。之所以这么称呼是因为这些点决定了我们划定的tube是否是合理的，这些点左右了tube的结构。 所以大致上来说，svr就是要找一条线，忽略它周围的点，对剩余的点进行回归。而对于Linear Regression来说，则是对每一个点都进行回归

Linear Regression 的计算公式是 $SUM(y-\hat y )^2 \rightarrow min$

SVR 的计算公式则比较复杂， $\frac{1}{2}||w||^2+c\sum_{i=1}^{m}(\xi_i+\xi_i^*)\rightarrow min$

补充资料： https://core.ac.uk/download/pdf/81523322.pdf

上面我们看到的是线性的支持向量回归，但是我们在接下来的例子中，却看到训练出来的模型是非线性的，这是因为我们使用了 Radial basis function kernel (径向基核函数)

我们可以先看看non-Linear SVR 长什么样

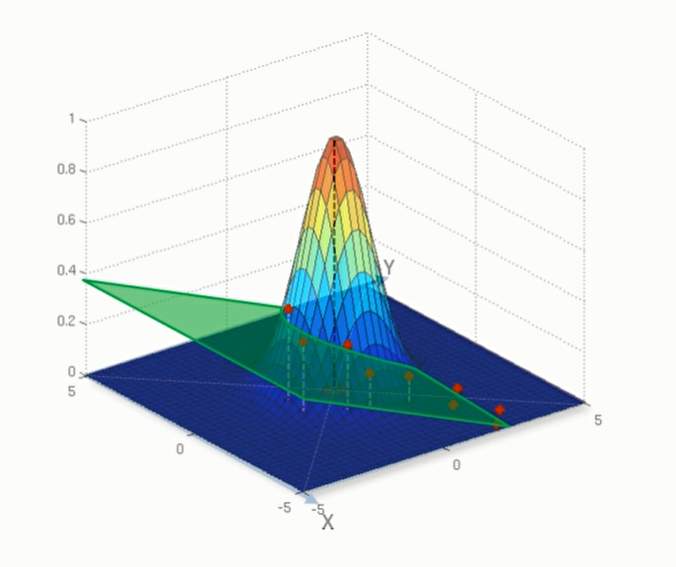
可以看到它们长得还是非常不一样的。要了解non-Linear SVR,还是需要用到为学习过的许多知识

  • Section on SVM:
    • SVM Intuition
  • Section on Kernel SVM:
    • Kernel SVM Intuition
    • Mapping to a higher dimension
    • The kernel Trick
    • Types of Kernel Functions
    • Non-Linear Kernel SVR

实验

这次我们使用的仍然是员工阶级和薪资的数据集。我们在进行试验的时候会遇到 Feature scaling (特征缩放)

在运用一些机器学习算法的时候不可避免地要对数据进行特征缩放（feature scaling），特征缩放可以使机器学习算法工作的更好。 如果某一列的值与其他列相比非常高，则具有更高值的列的影响将比其他低值列的影响高得多。 高强度的特征比低强度的特征重得多，即使它们在确定输出中更为关键。 因此，预测可能无法给出预期的结果，并且可能无法满足业务用例。

总而言之，功能缩放是必需的，因为：

  1. 回归系数直接受特征范围的影响
  2. 具有较高比例的功能比具有较低比例的功能更重要
  3. 如果我们具有缩放值，则可以轻松实现渐变下降
  4. 如果按比例缩放，某些算法将减少执行时间。
  5. 一些算法基于欧几里得距离，欧几里得距离对特征尺度非常敏感。

对于SVR来说，这是一个关于因变量的隐式函数，因此我们需要将数据进行特征缩放，来将员工的年龄和他的收入放到一个scale下进行建模。

对于简单线性、多项式线性回归，我们不需要利用特征缩放，因为可以找到能将高值和低值特征对应起来的系数。但是对于其他模型来说，在自变量x和应变量y之间他是找不到这样一个系数来对应的。这时候我们就会使用特征缩放。

另外，概率模型（树形模型）不需要归一化，因为它们不关心变量的值，而是关心变量的分布和变量之间的条件概率，如决策树、RF。而像Adaboost、SVM、LR、Knn、KMeans之类的最优化问题就需要归一化。

  • 当使用dummy variable的时候，没有必要再对其使用特征缩放了，因为本来就两个值0和1
  • 当因变量的值是0或者1的时候，也没有必要对其使用特征缩放了

Processing the dataset

那么我们现在来看数据集

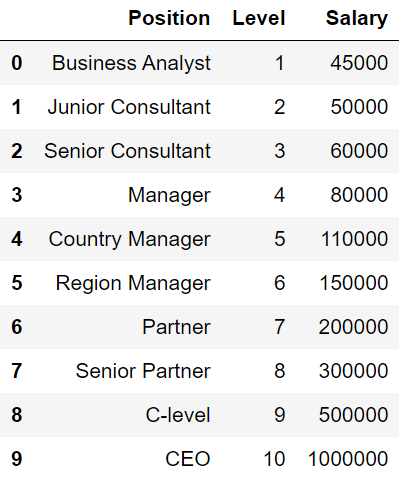
因变量从1到10，Salary从4500-1000000，它们之间的差距实在是太大了。这还会导致一些数据被误认成偏离值而被模型忽略。如果不进行特征缩放的话，那么SVR将完全不会起作用。所以我们要把自变量和因变量缩放到一个唯独下进行建模。

在特征缩放之前，我们首先将自变量和因变量分离：

1
2
3
dataset = pd.read_csv('Position_Salaries.csv')
X = dataset.iloc[:, 1:-1].values
y = dataset.iloc[:, -1].values

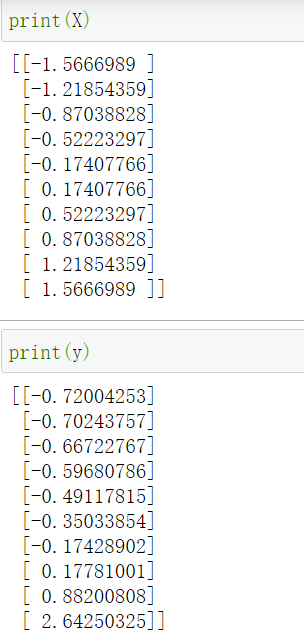
但是现在我们看到数组y实际上是一个一维数组，我们需要将其变成二维数组。这是因为 StandardScaler在进行特征缩放的时候只接收二维数组

1
y = y.reshape(len(y),1)

运用reshape函数，可以进行这样的转换，其中第一个参数是行数，第二个参数是列数。

Feature Scaling

现在我们进行特征缩放

StandardScaler原理: 去均值和方差归一化。且是针对每一个特征维度来做的，而不是针对样本。

标准差标准化（standardScale）使得经过处理的数据符合标准正态分布，即均值为0，标准差为1，其转化函数为：$x^* = \frac{x-\mu}{\sigma}$ ,其中 $\mu$ 为所有样本数据的均值， $\sigma$ 为所有样本数据的标准差

我们要注意，自变量和应变量应该选择不同的 StandardScaler，这是因为每列数据的均值和标准差都是不一样的

Training the SVR model on the whole dataset

在训练SVR模型之前我们要了解核函数的概念。

对于线性不可分的数据集，可以利用核函数（kernel）将数据转换成易于分类器理解的形式。

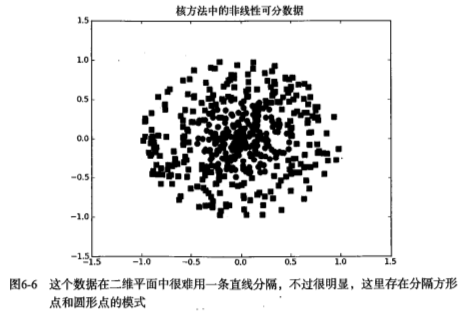
如下图，如果在x轴和y轴构成的坐标系中插入直线进行分类的话， 不能得到理想的结果，或许我们可以对圆中的数据进行某种形式的转换，从而得到某些新的变量来表示数据。在这种表示情况下，我们就更容易得到大于0或者小于0的测试结果。在这个例子中，我们将数据从一个特征空间转换到另一个特征空间，在新的空间下，我们可以很容易利用已有的工具对数据进行处理，将这个过程称之为从一个特征空间到另一个特征空间的映射。在通常情况下，这种映射会将低维特征空间映射到高维空间。比如将二维空间映射到一个合适的三维空间，那么就能找到一个合适的划分超平面来分离。如果原始空间是有限维，即属性数有限，那么一定存在一个高维特征空间使样本可分。这种从某个特征空间到另一个特征空间的映射是通过核函数来实现的。

https://www.jianshu.com/p/95e56d5126fd

径向基核函数是SVM中常用的一个核函数。径向基函数是一个采用向量作为自变量的函数，能够基于向量距离运算输出一个标量。

在python当中，我们从 svm中导入SVR并将其kernel参数设置为 rbf，然后再对X，y进行训练

1
2
3
from sklearn.svm import SVR
regressor = SVR(kernel= 'rbf')
regressor.fit(X,y)

Predicting a new result

现在我们通过训练好的模型来进行预测。注意了，我们传入的数据是特征放缩后的数据，我们预测出来的是特征放缩之后的结果，我们还需要用放缩尺将其还原成原来的数据

比如说我们要预测6.5级的员工薪水，传入一个二维数组(尽管只有一个数)

1
regressor.predict(sc_X.transform([[6.5]]))

这样返回的是在sc_y 标尺下的 薪水，打印出来得到：array([0.01150915])

接下来我们要做的就是将这个预测出来的数据还原回去,我们可以用 inverse_transform 来进行还原。

1
sc_y.inverse_transform(regressor.predict(sc_X.transform([[6.5]])))

打印出来的数据是： array([170370.0204065])

Visualizing the SVR results

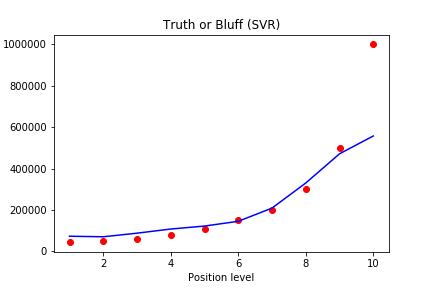
现在我们将SVR模型预测的结果画出来。

注意，这时候的X,y 是缩放后的，我们需要用 inverse_transform 来将其还原。因为x已经是二维数组了，我们就直接 regressor.predict(x) 即可

1
2
3
4
5
6
plt.scatter(sc_X.inverse_transform(X), sc_y.inverse_transform(y), color = 'red')
plt.plot(sc_X.inverse_transform(X), sc_y.inverse_transform(regressor.predict(X)), color = 'blue')
plt.title('Truth or Bluff (SVR)')
plt.xlabel('Position level')
plt.ylabel('Salary')
plt.show()

for higher resolution and smoother curve

我们将预测出来的曲线变得更加光滑：

原理就是将1-10 从原来的间隔1到现在的间隔0.1 ，然后再将其变成一个新的二维数组进行预测画图。这样曲线就会变得更加光滑。

1
2
3
4
5
6
7
8
9
X_grid = np.arange(min(sc_X.inverse_transform(X)), max(sc_X.inverse_transform(X)), 0.1)
X_grid = X_grid.reshape((len(X_grid), 1))
plt.scatter(sc_X.inverse_transform(X), sc_y.inverse_transform(y), color = 'red')
plt.plot(X_grid,
         sc_y.inverse_transform(regressor.predict(sc_X.transform(X_grid))), color = 'blue')
plt.title('Truth or Bluff (SVR)')
plt.xlabel('Position level')
plt.ylabel('Salary')
plt.show()

-------------本文结束，感谢您的阅读-------------