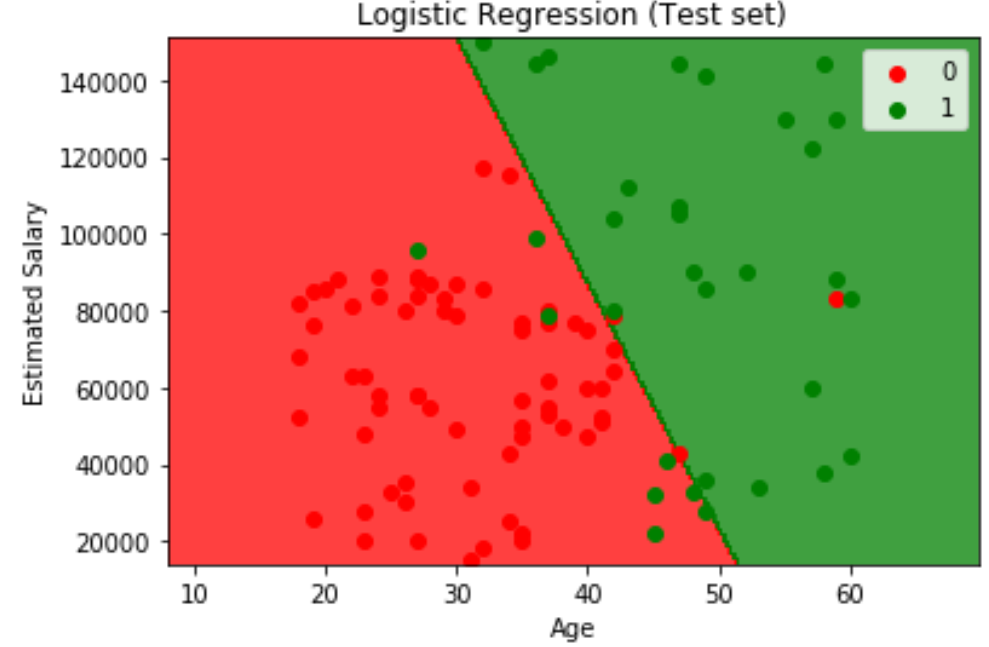
Logistic Regression

学习自：https://www.jianshu.com/p/3254560624b7

我们之前谈论的都是线性回归问题，线性回归问题一般解决的时自变量和应变量存在线性关系的数据。比如说下面这张图。

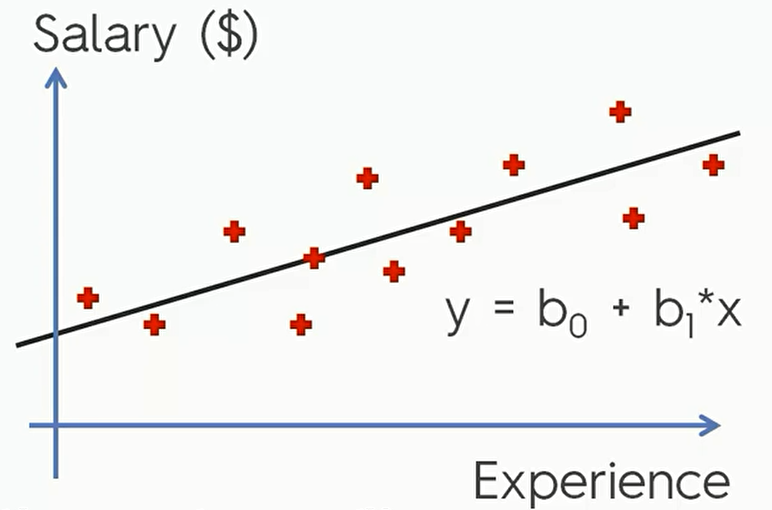
但是对于这种数据，是一些关于年龄信息和客户是否购买产品的数据线性回归就很难满意的完成我们的任务，因为因变量只有0和1：

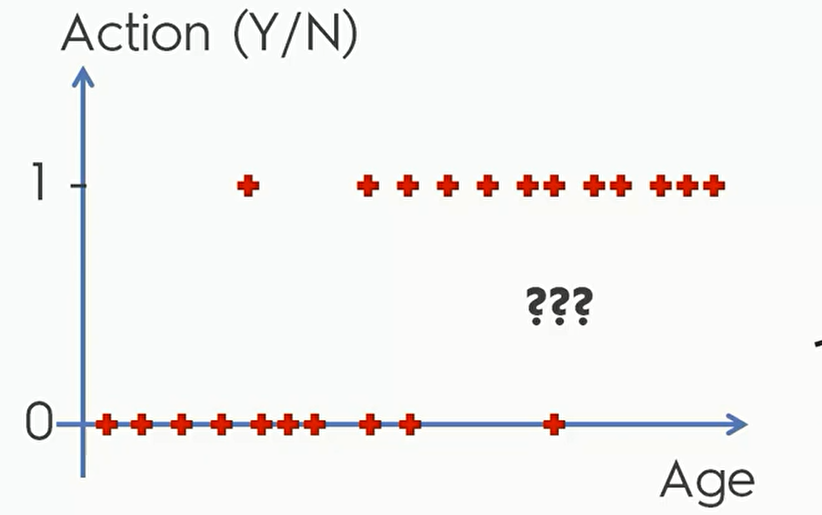
这时候如果强制线性回归，就会出现这样的结果。

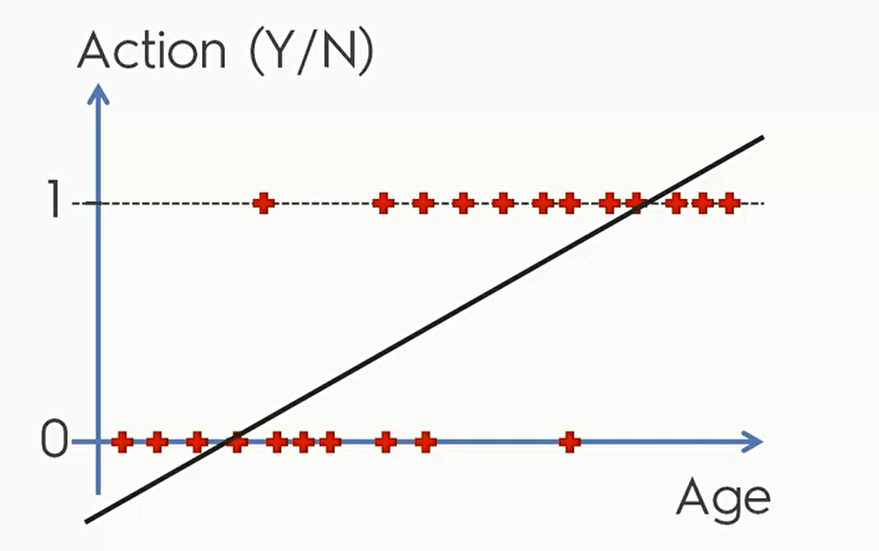
这显然不是我们想要的，年龄低于某个值的时候Action变成了负数而高于某个值得时候竟然大于1. 于是，我们要引入分类器的概念，我们现在就来看看第一个分类算法：逻辑回归

逻辑回归可以参考高中生物的逻辑斯蒂增长曲线，公式为 $\ln(\frac{p}{1-p}) = b_0+b_1*x$ (p 代表了是否会发生的概率)

将其应用于上面的数据，我们就会得到一个新的图像，其中y轴的单位是 $\hat p (Probability)$ ,我们可以用这条曲线来预测中间年龄段的人是否会购买产品

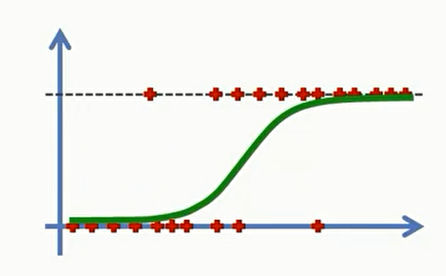
我们可以看看具体数据，假设当前有几个数据分别是年龄20、30、40、50。那么其在纵坐标上对应的结果也可以标记出来，得到不同的概率。

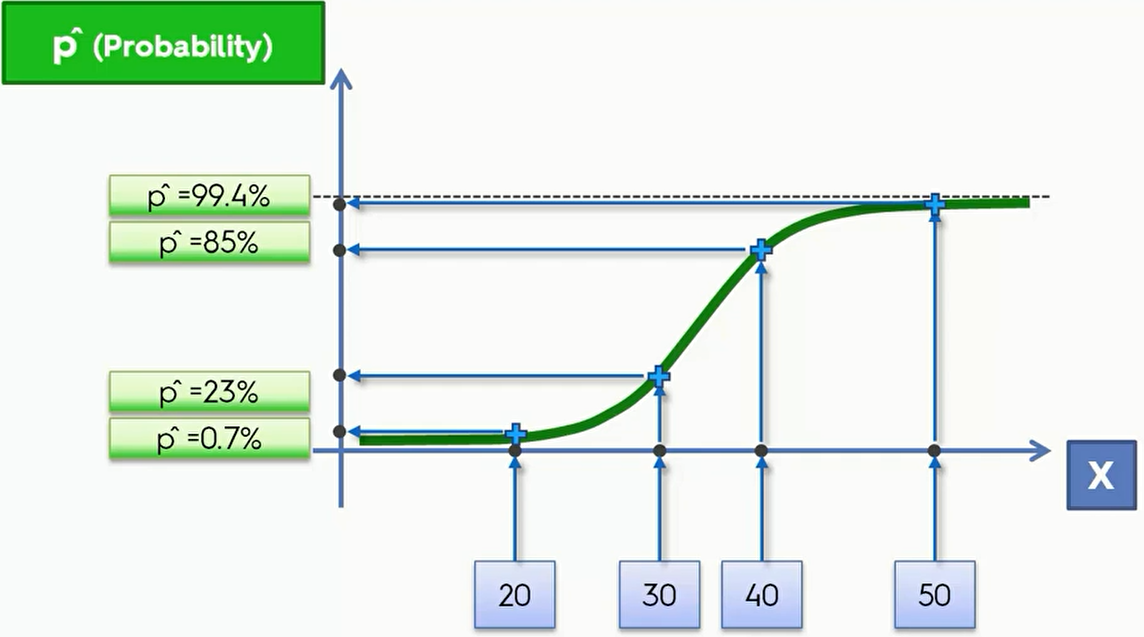
关于年龄和是否会购买的预测，我们可以在 0.5 处画一条直线，在直线下的用户我们可以将其y值设置为0，直线以上的就可以预测用户会购买。

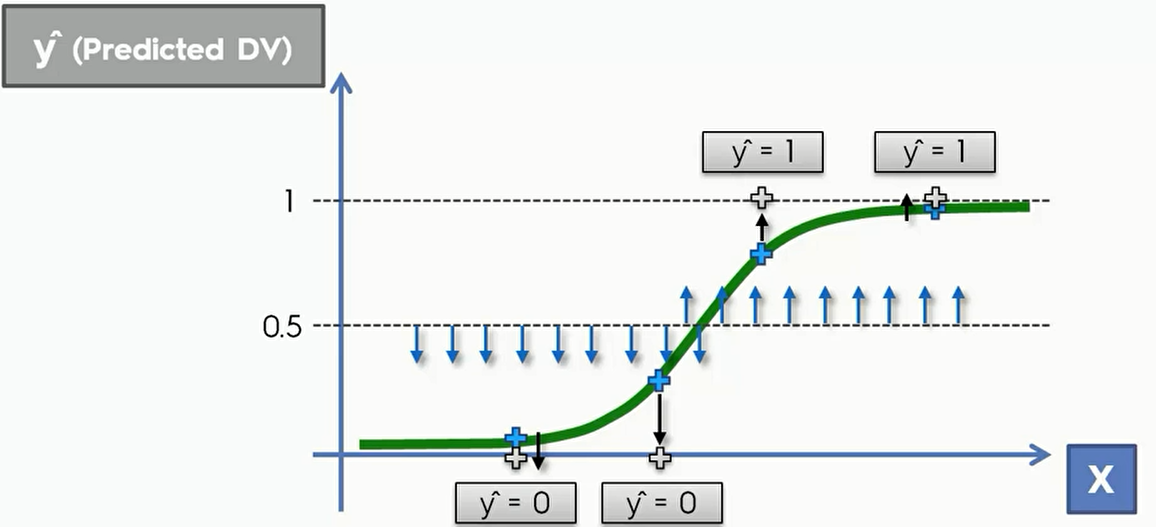
代码

我们下面就对一个比较真实的数据集进行逻辑回归的分类. 其中 Feature是 Age和EstimatedSalary，需要被预测的值是 Purchased。一共有400行数据，没有缺失值，不需要进行数据清洗。

假设你是一家车厂的销售经理，我们拿到了一些之前顾客的年龄和预期薪资和他们的购车情况，我的任务就是去选择什么人群有更多的可能会购买我们车厂新出的车型。

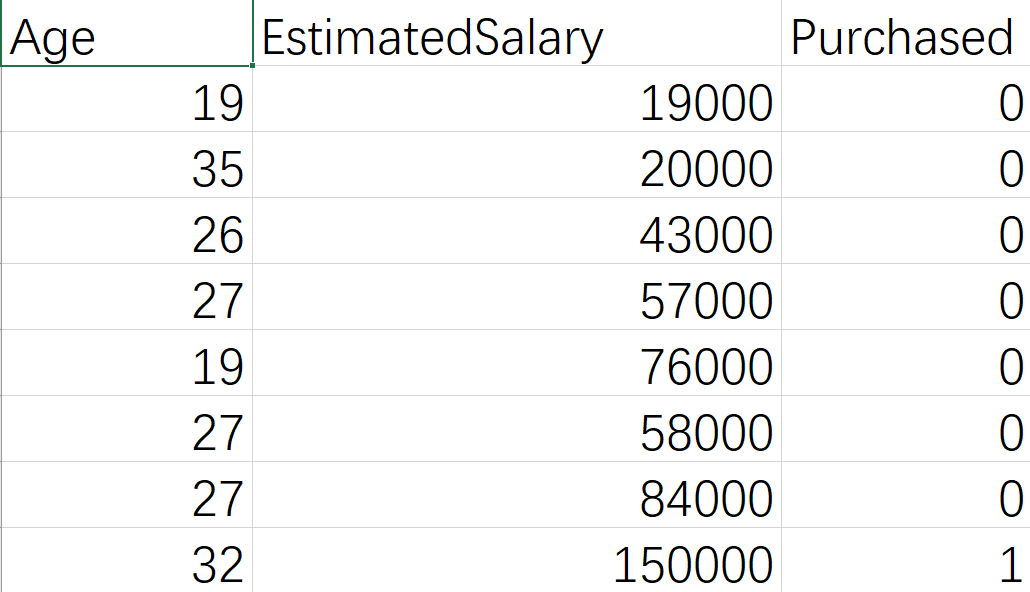
接下来我们会一步步进行逻辑回归。以后对于其他数据集，也可以使用这个模板：

首先我们进行导库、训练集测试集切割

Importing the Libraries

1
2
3

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

Importing the dataset

1
2
3

dataset = pd.read_csv('Social_Network_Ads.csv')
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, -1].values

Splitting the dataset

我们将测试集设为整个数据集的25%，将训练集设为数据集的75%

1 2	from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)

Feature Scaling

然后我们现在要判断是否需要 Feature Scaling

首先我们要知道逻辑回归模型不一定都要进行特征放缩(不同于一定要进行放缩的SVM)，但是对一些特征进行放缩可能会提升整个模型的性能。我们就要看看这个数据集的特征是否需要被放缩。

我们这个数据集，有两个Features：年龄和收入，这两者的均值相差很大，肯定不是一个维度下的，于是需要对其进行特征放缩。而预测的是他们是否会购买，值为0或者1，所以不用对预测值进行特征放缩

from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)

我们需要对测试集和训练集都进行特征放缩。

Training the Logistic Regression model

接下来我们来训练逻辑回归模型。很简单，从 sklearn.linear_model 模块中导入LogisticRegression类。

因为现在我们做的是分类而不是回归，所以我们从回归器(regressor) 变成了分类器(classifier).

现在我们知识初步学习一下逻辑回归模型，所以对其中的参数并没有很多的要求，只要将 random_state 设置为0即可。

1
2
3

from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression(random_state = 0)
classifier.fit(X_train, y_train)

Predicting

Predicting a new result

1	print(classifier.predict(sc.transform([[30,87000]])))

打印得到 [0]，说明对于30岁，年入87000美元的人来说，他大概率不会购买这辆车。

Predicting the Test set results

1
2
3

y_pred = classifier.predict(X_test)
print(np.concatenate((y_pred.reshape(len(y_pred),1),
                      y_test.reshape(len(y_test),1)),1))

然后我们对测试集进行一个预测，并将预测出来的结果和原来的结果进行一个比对。注意，这里要做一个形状转换，将他们都变成竖着排列的。

打印得到：

肉眼可见大多数情况都预测成功了，只有少数几组数据没有预测成功

Making the Confusion Matrix

Confusion Matrix 是混淆矩阵，是表示精度评价的一种标准格式，用n行n列的矩阵形式来表示。具体评价指标有总体精度等。

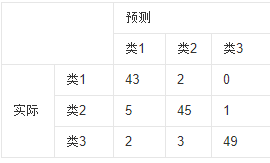
混淆矩阵的每一列代表了预测类别，每一列的总数表示预测为该类别的数据的数目；每一行代表了数据的真实归属类别，每一行的数据总数表示该类别的数据实例的数目。每一列中的数值表示真实数据被预测为该类的数目

如下图，第一行第一列中的43表示有43个实际归属第一类的实例被预测为第一类，同理，第一行第二列的2表示有2个实际归属为第一类的实例被错误预测为第二类。

我们用python的confusion_matrix也可以来做这个模型的混淆矩阵，只要将y_test,y_pred传入即可

from sklearn.metrics import confusion_matrix, accuracy_score
cm = confusion_matrix(y_test, y_pred)
print(cm)
accuracy_score(y_test, y_pred)

打印得到下面的数据：说明第一类(0)有65组数据预测成功，3组数据预测失败；第二类(1)有24组数据预测成功，8组数据预测失败

1 2	[[65 3] [ 8 24]]

accuracy_score:

一共有100组数据，11组预测失败，成功的概率为89%，于是accuracy_score = 0.89

0.89

Visualising

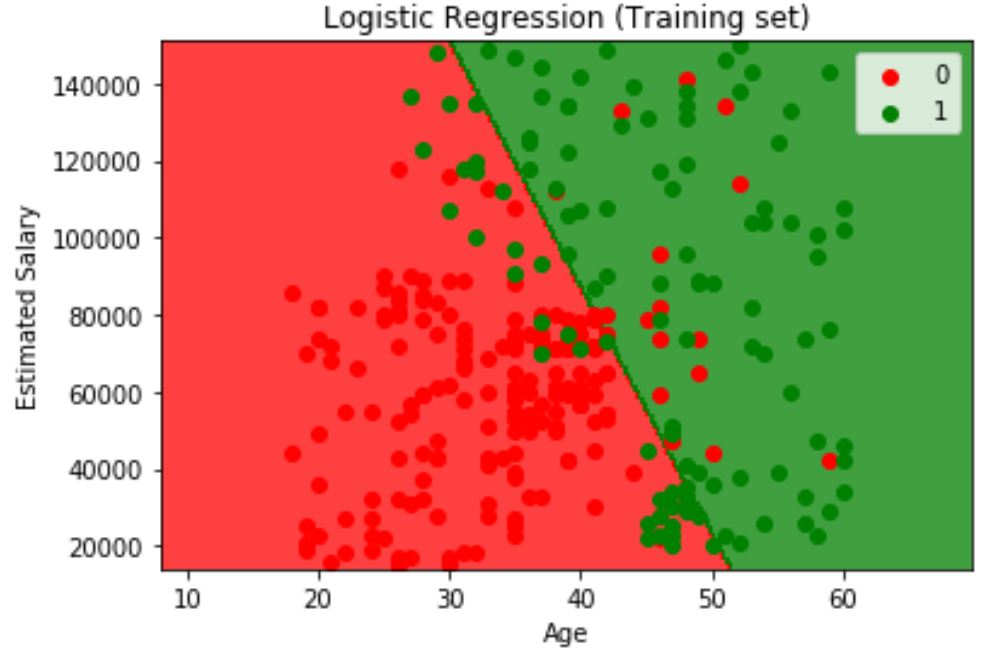
现在我们做一个可视化操作，可以很直观地展现整个模型的效果。我们的图像将达到三个效果

我们将用一个2维图展现，其中x轴、y轴分别是年龄和薪资两个特征。
我们将用每一个点表示一个顾客的信息，并用不同的颜色将他们的购买情况区分开来
我们将用颜色区分开两个不同的预测区域，并在中间画出分界线。

Visualising the Training set results

from matplotlib.colors import ListedColormap
X_set, y_set = sc.inverse_transform(X_train), y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 10, 
                               stop = X_set[:, 0].max() + 10, 
                               step = 0.25),
                     np.arange(start = X_set[:, 1].min() - 1000, 
                               stop = X_set[:, 1].max() + 1000, 
                               step = 0.25)
                    )
plt.contourf(X1, 
             X2,
             classifier.predict(sc.transform(np.array([X1.ravel(), X2.ravel()]).T)).reshape(X1.shape),
             alpha = 0.75,
             cmap = ListedColormap(('red', 'green')))

plt.xlim(X1.min(),X1.max())
plt.ylim(X2.min(),X2.max())
for i, j in enumerate(np.unique(y_set)):
    plt.scatter(X_set[y_set == j, 0],
                X_set[y_set == j, 1],
                c = ListedColormap(('red', 'green'))(i),
                label = j)
plt.title('Logistic Regression (Training set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()

Logistic_Regression