SVM and KernelSVM
SVM
部分文字摘自 https://www.jianshu.com/p/0b09dc432081
现在我们仍然有两类,一类红点一类绿点

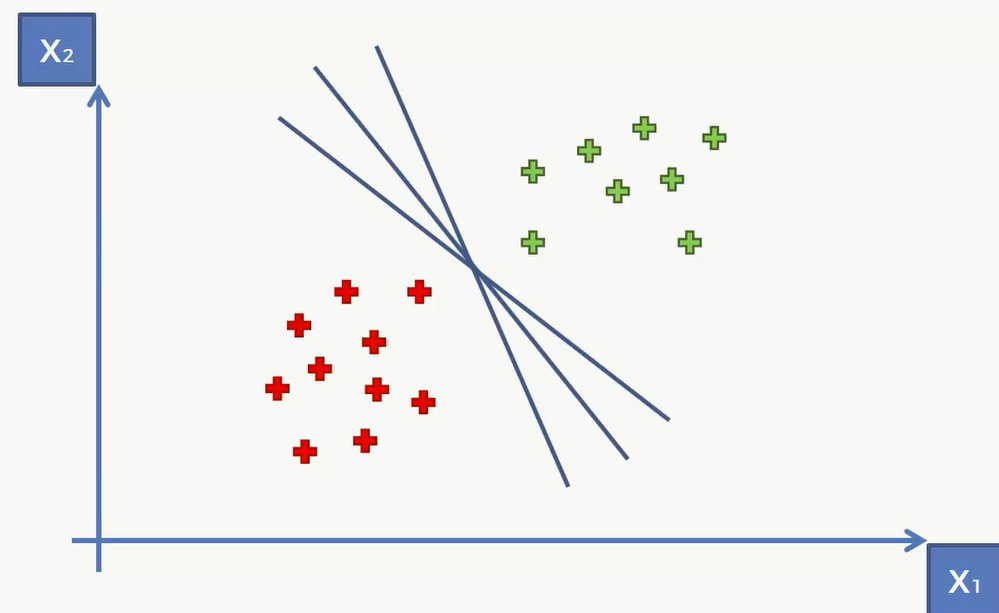
现在我们要做的是如何将这两种数据准确的分隔开来。看图像其实很简单,可以横着画一条直线或者竖着画或者斜着画都能将其分隔开来。那么svm要做的就是找到最佳的一条直线。
那么这条直线要满足的特点是它和红组和绿组有最大的间隔。所谓最大间隔就是红组中离直线最近的点的距离和绿组中离直线最近的距离最大。这两个点就叫做Support Vector。这里解释下为什么叫支持向量,首先“支持”的意思,就是说这些数据点中除了两个点之外的任何一个点都不会影响到这个算法的决策边界,即这条直线实际上是由这两个点支持的,然后“向量”,在二维空间中的点实际上都可以用向量表示,但在高维中没办法用几何方式表示出来,它其实都是向量。
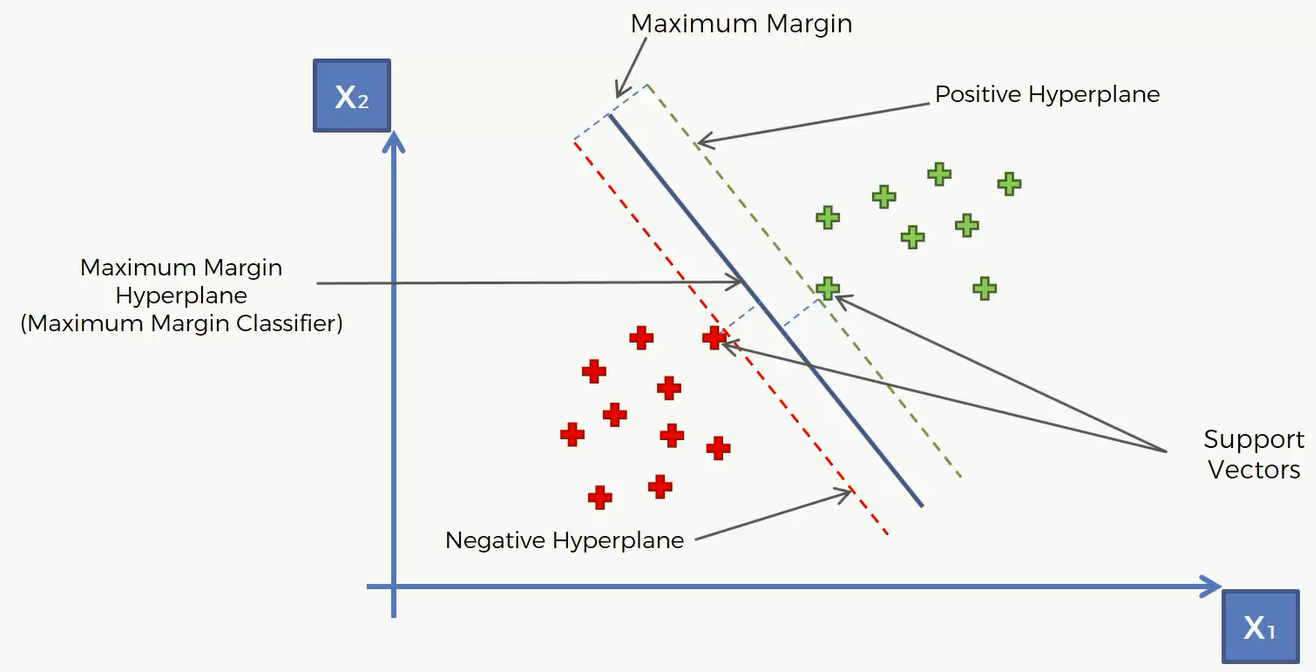
对于这条直线,我们称作Maximum Margin Hyperplane/Classifier,即最大间隔超平面。所谓超平面就是比数据空间少一维的空间,比如这里二维的那么对应的就是一维的即一条直线。其中和这条直线平行的这两条直线,一个叫做正向超平面,一个叫负向超平面,这个正负这里只是跟法向量有关,是数学上的概念,不用太在意正负。
接下来看看这个SVM算法为什么这么特别(与其他的算法相比):
这里假设我们需要训练一个算法来识别苹果和橘子,比如通过水果的颜色和水分来判断。那么大部分的苹果都是青色或者红色,而橘子一般是黄色。那么在图像中可以当作这个横轴代表颜色,x1越往右的就是颜色偏黄色的,那么这部分数据显然都是橘子。
在其他的机器学习算法中,机器只会关注特别经典的数据,比如说下图中圈出来的两部分。也就是其他算法都只关注非常红、非常绿的苹果或者非常黄的橙子。
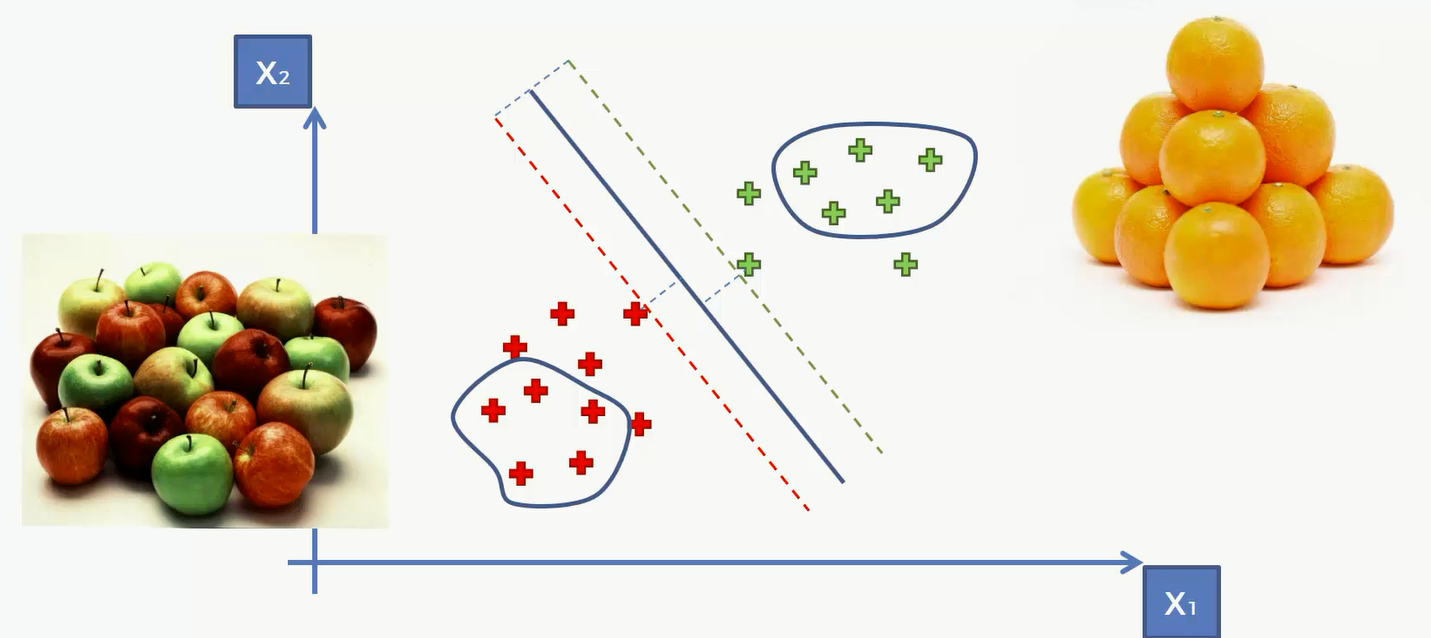
但是SVM却不一样了。SVM最特别的地方就是它可以学习到最特殊最特别的东西,比如说这个时候出现了一个黄色的苹果,很像橘子。那么这样的苹果就是SVM中的支持向量,同样如果这时有个绿色的橘子也是支持向量。因此SVM其实是由数据中比较极端的个例所实现的。这点和其他的算法有根本的不同。
代码
我们用的还是老的数据集,所以前面的代码都可以照抄 逻辑回归中的代码,只需要改建模这一块即可
这里我们要用的还是线性的核函数,所以我们将kernel 设置为 linear
1 | from sklearn.svm import SVC |
然后我们看看SVM的预测情况
1 | from sklearn.metrics import confusion_matrix, accuracy_score |
1 | [[66 2] |
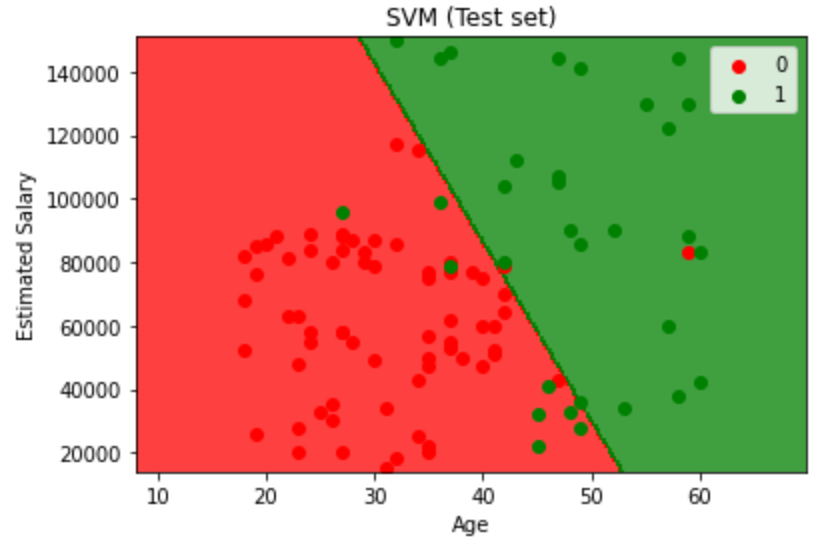
最后来看看可视化之后的样子:
1 | from matplotlib.colors import ListedColormap |
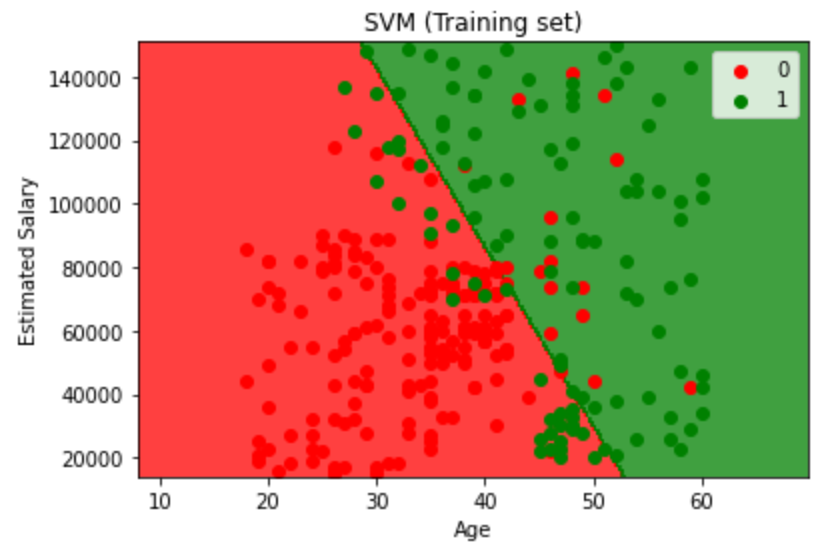
1 | from matplotlib.colors import ListedColormap |
Kernel SVM
SVM是让我们在两组数据中划出一条分界线,那么如果我们没办法再两组数据中滑出一条分界线怎么办?
对于非线性的数据,我们又该怎么办?因此我们须要改良SVM算法,这就是接下来的 和函数支持向量机(Kernel SVM)
高维投射
对于下面这些离散的非线性的数据,我们是没有办法直接画一条线将它们分割开的
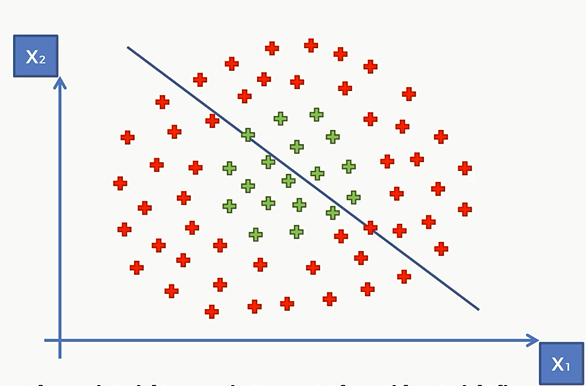
所以我们该怎么办?首先,我们先将线性不可分的数据从低维投射到高维,使得其在高维上线性可分,接下来再将分隔好的数据投射到原先低维的空间。
这里先举一个一维的问题。这里有一条直线上,有红色和绿色的点,这条直线上是否存在一个点将红点和绿点分开。显然是无法做到的,那么需要将其投射到二维空间上。

我们假设红点和绿点在左侧的分界线是5,那么就将其全部减去五然后求其平方得到一根曲线
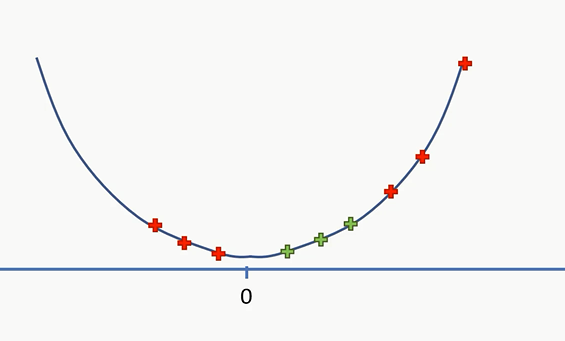
现在,我们就能用一根直线将红点和绿点分开了。
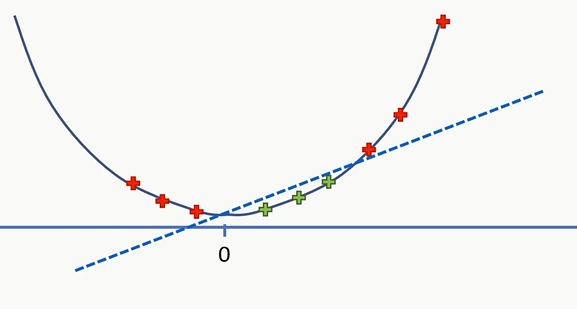
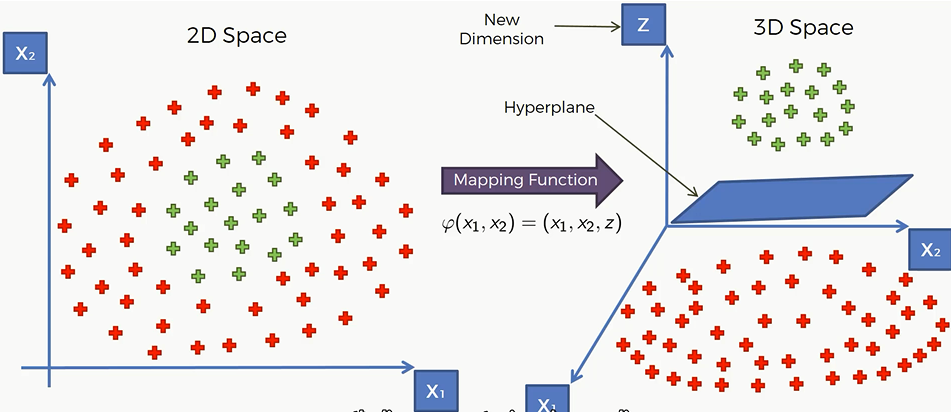
那么我们也可以将这个原理运用在二维空间上:
通过一个很奇怪的映射函数,我们可以将二维的点投射到三维空间上。然后我们就可以找到一个平面(Hyperplane)将两类点分开来
然后我们在将其投射到二维空间上,就可以将两类点分开了
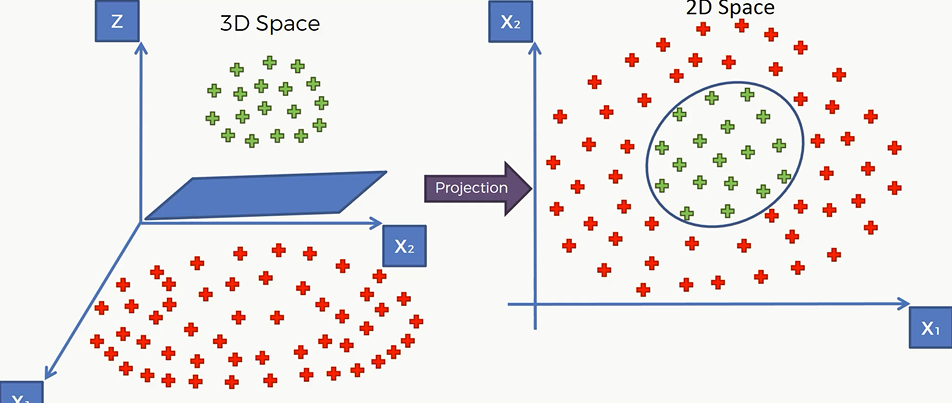
但由于低维映射到高维然后再让高维投影到低维,对于计算机而言计算量很大,那么我们就需要引入核函数来解决非线性问题,可以绕过这里的繁琐的计算过程,却依然能解决问题。
高斯核函数(RBF)
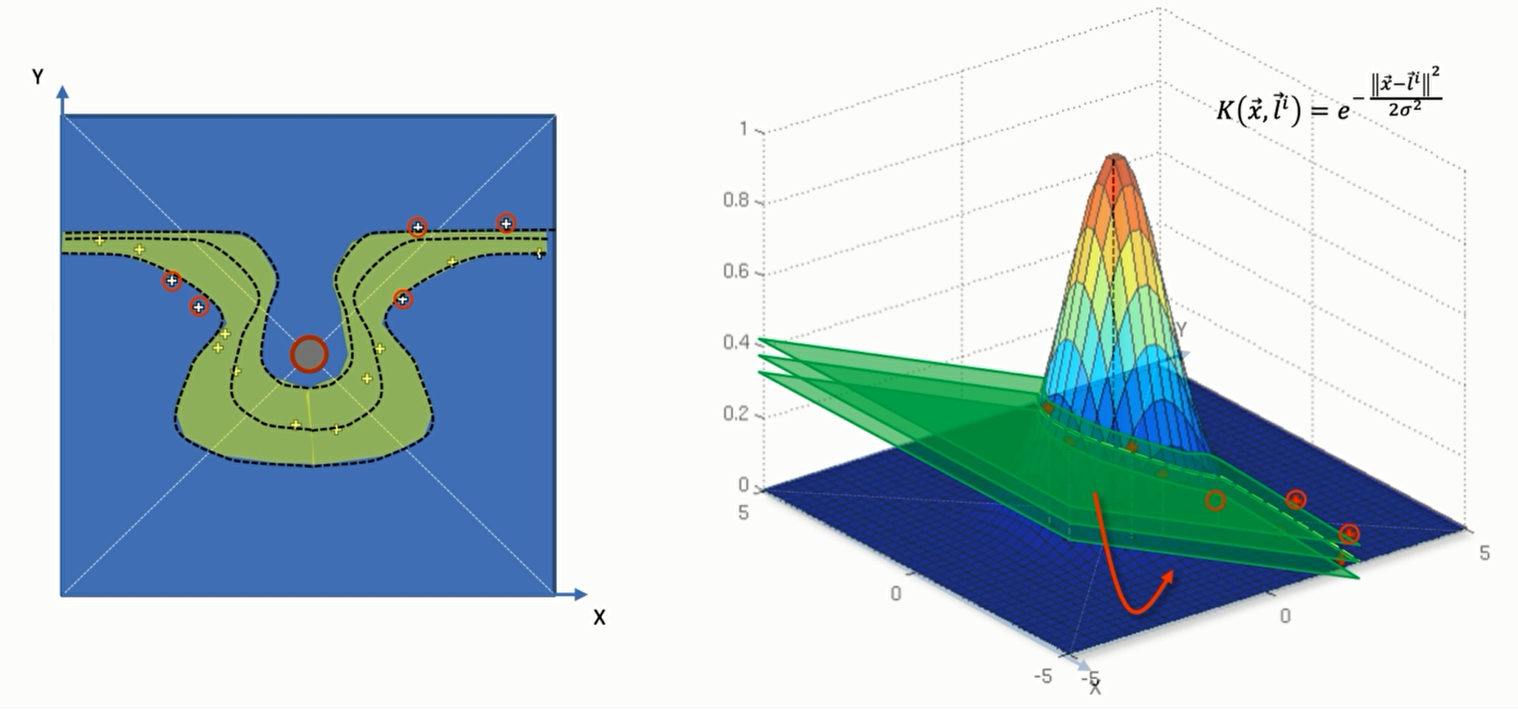
高斯核函数的公式 :$K(\overrightarrow{x},\overrightarrow{l^i}) = e^{-\frac{||\overrightarrow{x}- \overrightarrow{l^i}||^2}{2\sigma^2}}$
K 代表了 Kernel,也就是对于两个向量核函数。
$\overrightarrow {x}$ 代表了表示点的那个向量
$\overrightarrow{l^i}$ 就是核函数的中心,因为核函数可能有多个中心,所以 $l$ 具有上标 i
$\sigma$ 为函数的宽度参数 , 控制了函数的径向作用范围。
我们用一个可视化的方式来解释高斯核函数
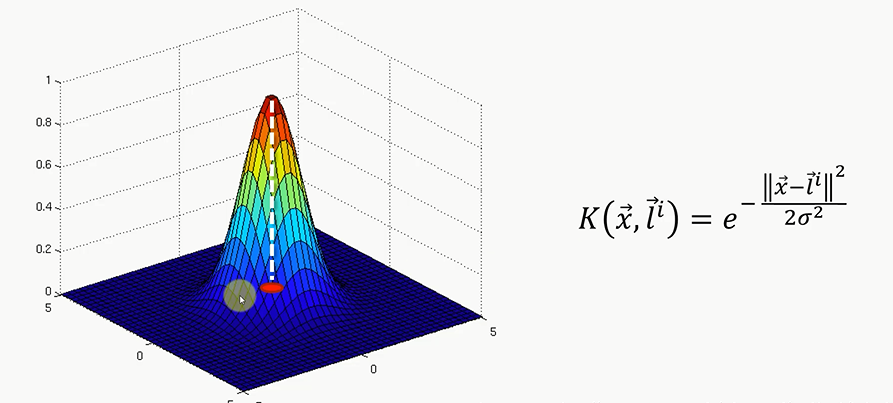
我们设坐标(0,0,0) 为和函数的中心(只有一个)。也就是二维平面中绿色区域的中心
那么左边这幅图画就是这些红色和绿色的点通过高斯核函数在三维空间中的映射。
这里从图像也能看出来,红点距离中心点是比较远的,那么 $||\overrightarrow{x}- \overrightarrow{l^i}||^2$ 就会比较大,由于是负数,那么整个方程的结果就会趋向于0.如果x与l距离很接近,那么$||\overrightarrow{x}- \overrightarrow{l^i}||^2$就会趋向于0,加个符号依然趋向于0,那么这个函数就趋向于1.
那么接下来看看如何利用这个函数来寻找数据的分类边界。函数中的l我们可以当作基准点,在上述的数据中如图假设是绿色点的中心,那么很显然,所有的绿色点距离这个点的距离一定是小于某个常数,而红色的点距离它的距离一定大于这个常数。
那么在二维平面,在训练SVM的时候,模型里面就会对”映射出来的” 高维空间画一个圈,这个圈的纵坐标并不是0但是很接近0。在这个圈里面的,也就是z轴大于这个圈的高度的,就属于绿色的点,反之则属于红色的点。
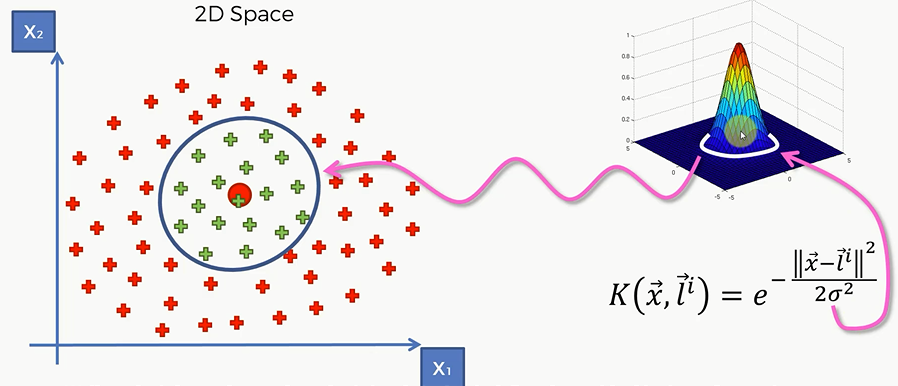
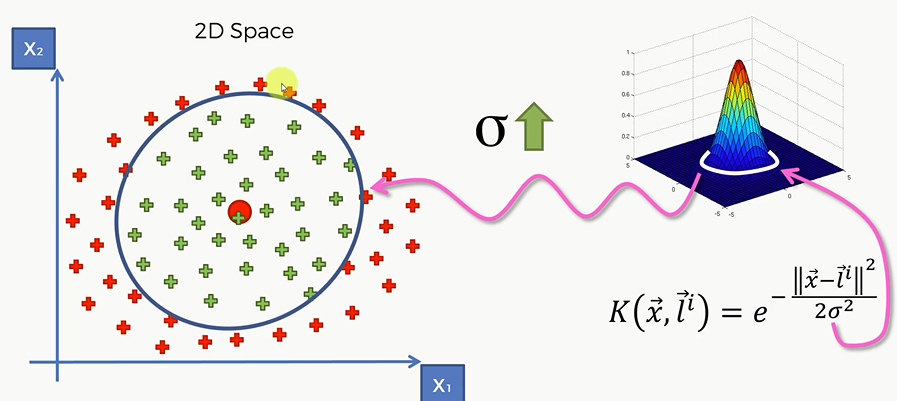
那么这个 $\sigma$ ,就决定了函数的径向作用范围。也就是这个”圈“ 的大小。$\sigma $ 是由函数通过训练自己取的。如果 $\sigma$ 增大,那么我们看到就会有更多的原本属于红色的点被划分为绿色去了.
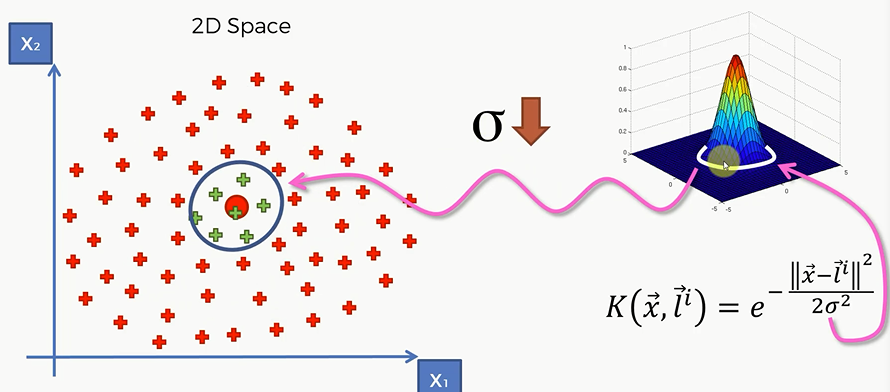
反之$\sigma$ 减小,那么很多原本属于绿色的点被划分到红色去了
假如说现在我拿到了一个更加复杂的数据集,红点和绿点的分布如下:
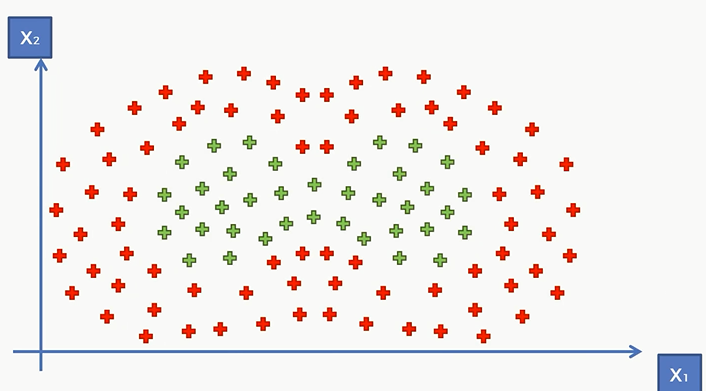
这时候规定一个中心已经是不可能的了,我们需要确立两个中心
公式就变成了 $K(\overrightarrow{x},\overrightarrow{l^1})+ K(\overrightarrow{x},\overrightarrow{l^2})$
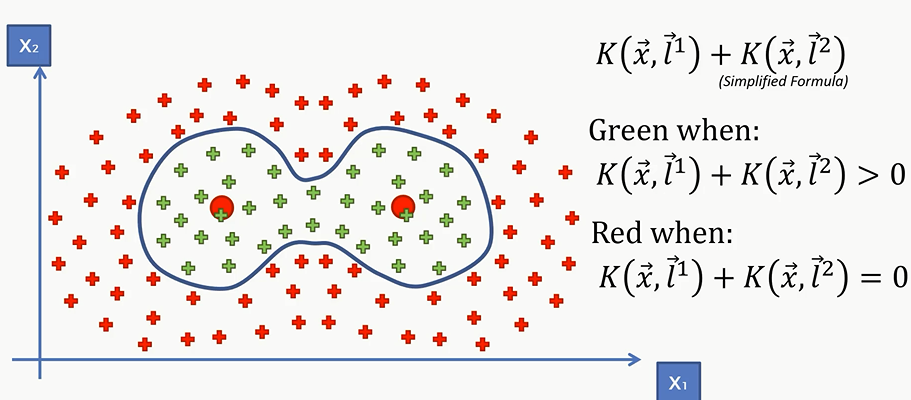
对于左边那个中心来说,它只负责左边的绿色的点的核函数大于0;而对于右边绿色的点和所有的红色的点的核函数都等于0;对于右边的中心来说则刚好相反,那么我们就可以用 $K(\overrightarrow{x},\overrightarrow{l^1})+ K(\overrightarrow{x},\overrightarrow{l^2})$ 是否大于0,来判断新的点是属于红色还是属于绿色。
Types of Kernel Functions
我们要知道有很多种的核函数:它们的功能各不相同

Non-Linear Kernel SVR
我们假设现在拿到了这样一系列数据:

对于这样的数据,我们显然不能用普通的线性支持向量机
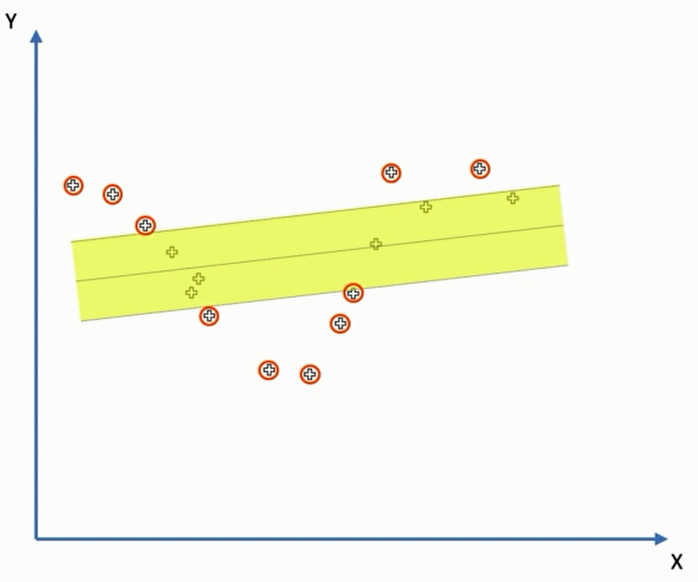
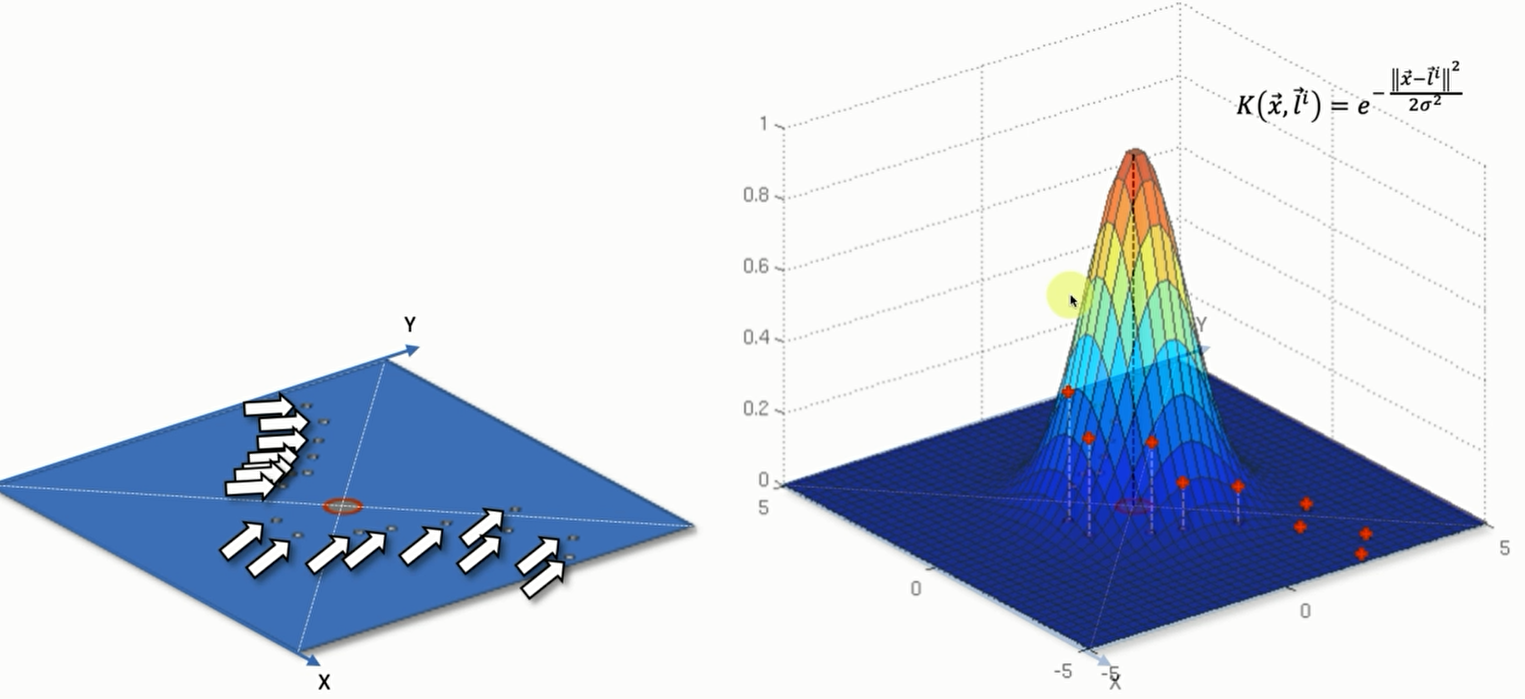
于是我们采用 Non-Linear SVR,也就是用高斯核来进行拟合。首先画一个二维平面和一个三维空间,并将这些点用高斯核函数映射到三维空间当中去:
接着我们就可以根据三维空间中的点来画出 超平面 。超平面与核函数相交并投影到二维平面上的曲线就是非线性支持向量机模拟出来的曲线了。
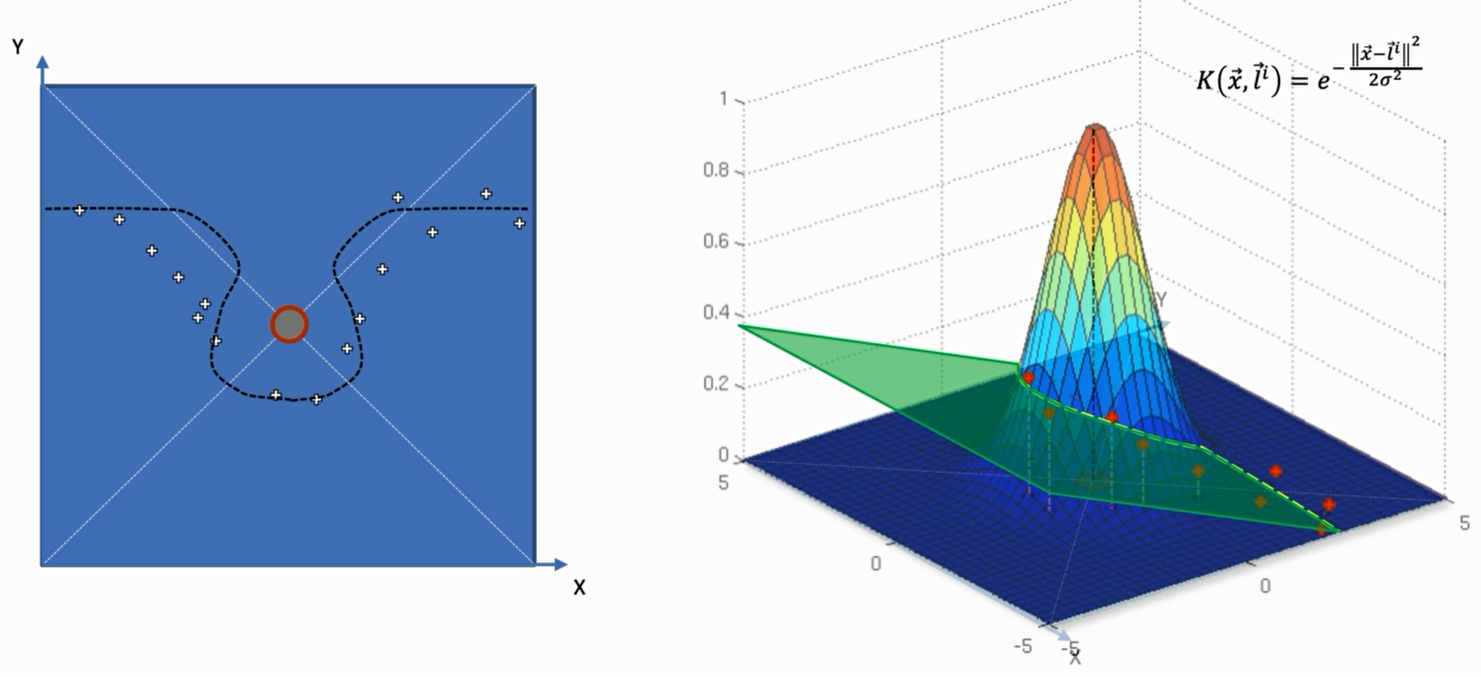
那么你也许会问 线性的SVM有 $\epsilon$ ,在非线性空间中是否有呢? 答案是有的,只不过这时候 $\epsilon$ 变成了平面和平面之间的举例
代码
现在我们利用核函数支持向量机来进行分类:
经过导入、特征缩放之后进行训练
1 | from sklearn.svm import SVC |
然后,我们进行预测:
1 | y_pred = classifier.predict(X_test) |
现在我们看看SVM的混淆矩阵和分数
1 | from sklearn.metrics import confusion_matrix, accuracy_score |
1 | [[64 4] |
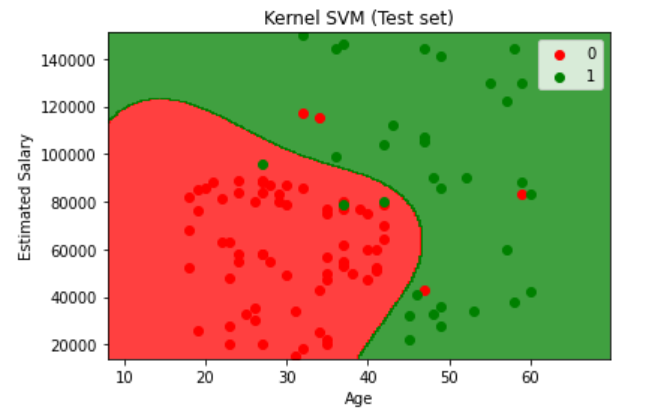
最后我们来可视化结果:
1 | from matplotlib.colors import ListedColormap |
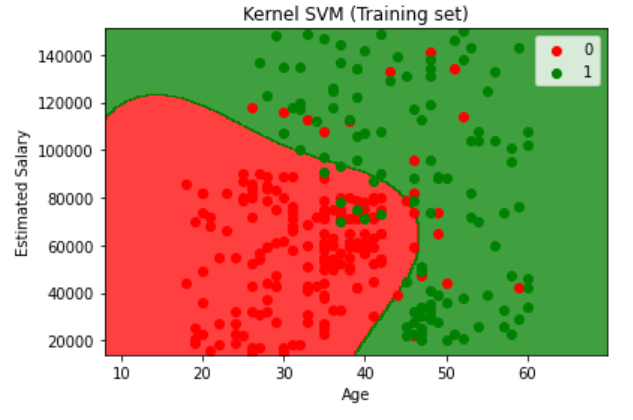
1 | from matplotlib.colors import ListedColormap |