朴素贝叶斯
参考博客: https://www.jianshu.com/p/456782eff870
我在离散数学的概率博客中提到了Bayes 定理,可以参考这篇博客进行学习: Bayes‘ Therem
Naïve Bayes
现在我们着重介绍一些朴素贝叶斯分类器。
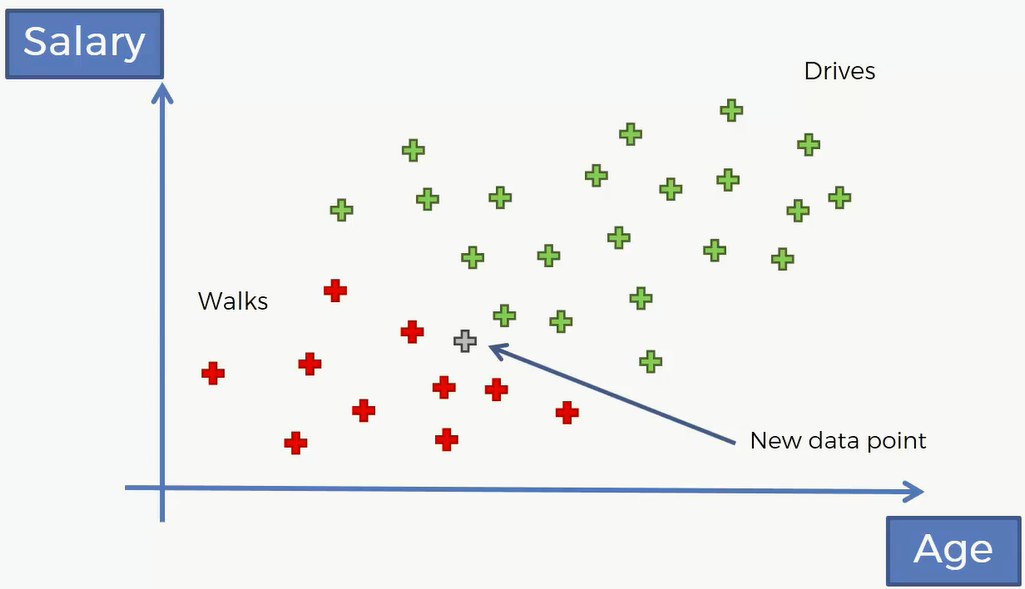
这是一个年龄薪水关于上班方式的数据集,绿色代表了了开车去上班,红色代表了走路去上班。现在有一个新的点进来了,我们该怎么预测它是属于哪一类的呢?
我们需要用到 $P(A|B) = \frac{P(B|A)\cdot P(A)}{P(B)}$ 其中P(A|B)被称作后验概率,P(B|A)和P(B)这两个概率并不完全是概率,因为朴素贝叶斯分类器中,B代表特征,所以说这两个概率我们称作似然。
Step1
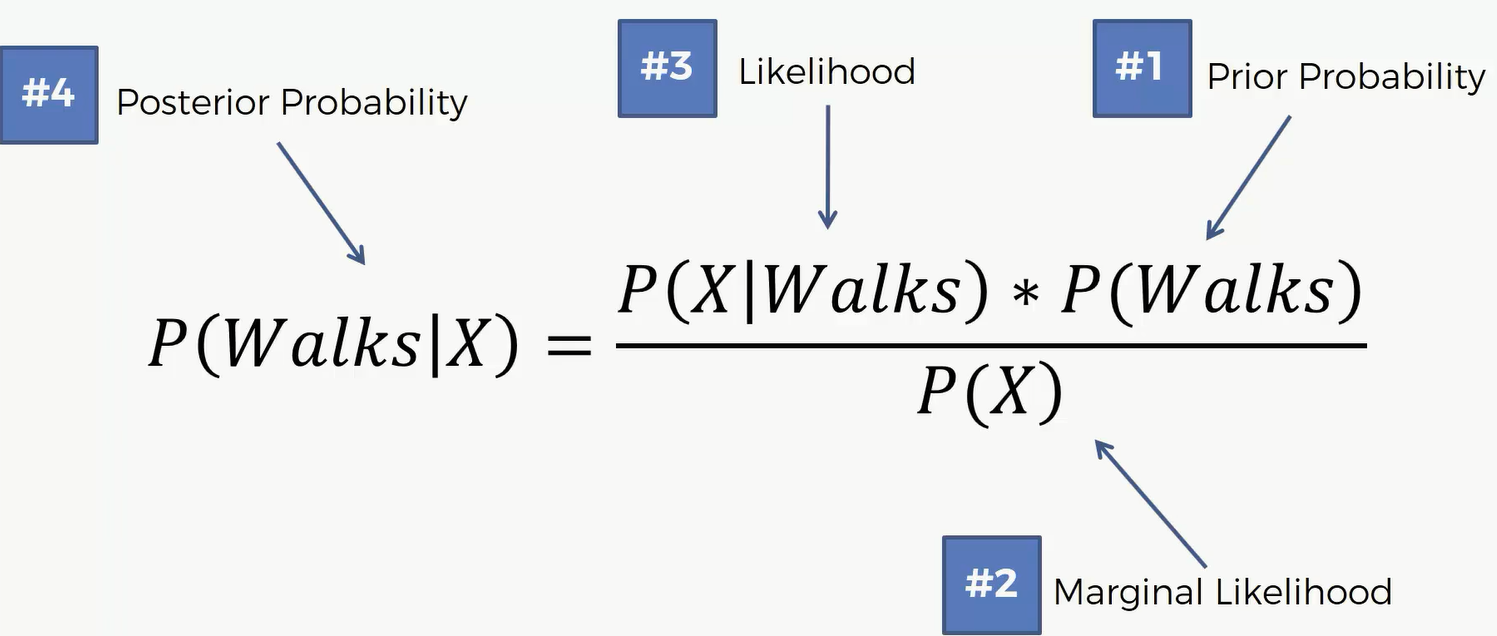
应用到上面这个数据集,我们就会求 $P(Walk|X)=\frac{P(X|Walk)*P(Walks)}{P(X)}$
这里的X就是它的特征。对于新的点,它有对应的年纪和收入就是这个新用户的特征,我们要求的就是已知这些特征,要得到它分到红组或者绿组的概率。这里的P(Walks)就是随机抽一个人,它是走路上班的概率,这个也被称作先验概率,对应的就是后验。P(X)指的是随机抽一个人,他所显示的特征和新用户的特征的似然或者可能性。这里的似然也是个概率,它是对数据特征的概率,因此我们把它叫做似然。再然后,这里的P(X)指的是对这个数据特征的概率,因此叫做似然。接下来第三部要求的也是个似然P(X|Walks),或者叫做边际的似然,边际的可能性。这样我们就能求出后验概率P(Walks|X)。
Step2
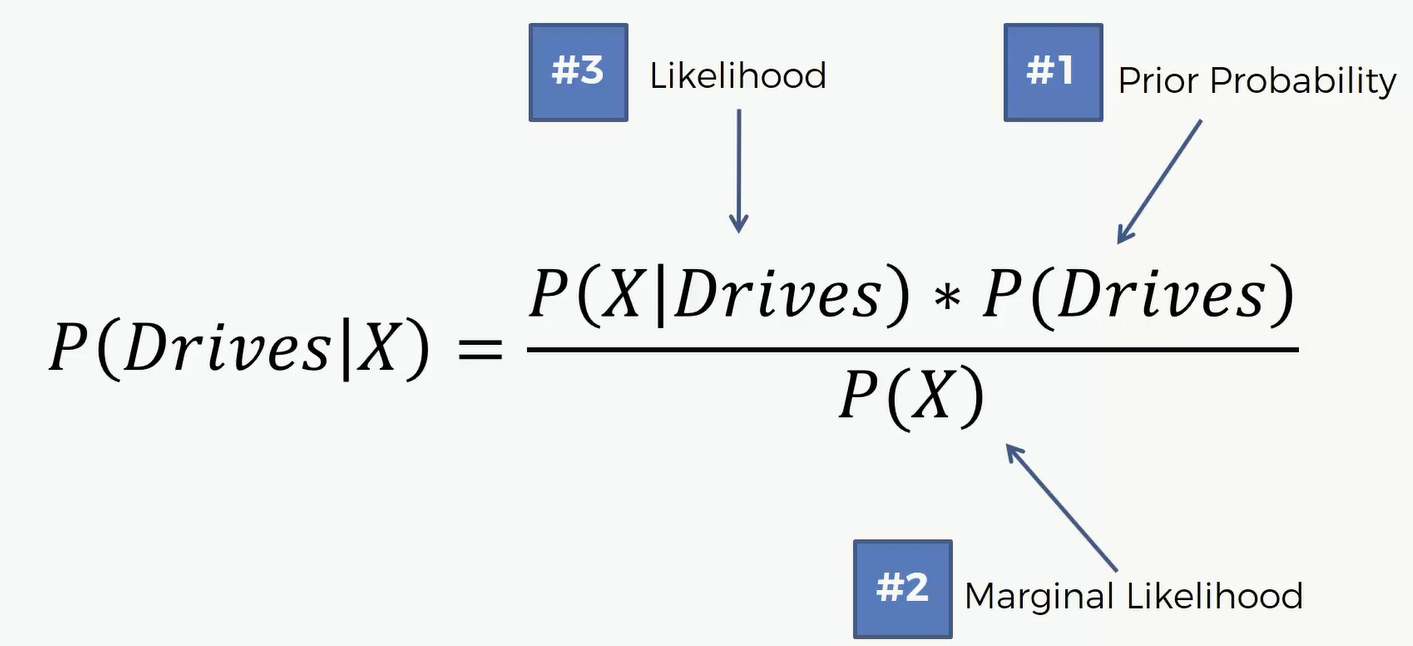
分别计算出 Drives和Walks的概率之后,我们要比较 $P(Walks|X) ~v.s. P(Drives|X)$ 谁大谁小,哪个大这个X就属于哪里
我们来一步一步实现这些步骤
首先 P(Walks) = (Number of Walkers)/ (Total Observations) = 10/30
接下来,计算P(X),也就是似然。这个是朴素贝叶斯中核心的一步。这里的X指的是新用户他所代表的特征,即年纪和收入。我们可以围绕这个新用户画一个圈,那么这个圈就代表着在这个二维数据空间中的所有用户,他们的特征和新用户非常相似。要求的P(X)就是我们原先数据空间中的所有数据,它的特征坐落在这个圈中的概率。那么我们要计算的就是原先数据中与新用户拥有相似特征的个数除以总的人数。 P(X) = Number of Similar Observations/ Total Observations = 4/30
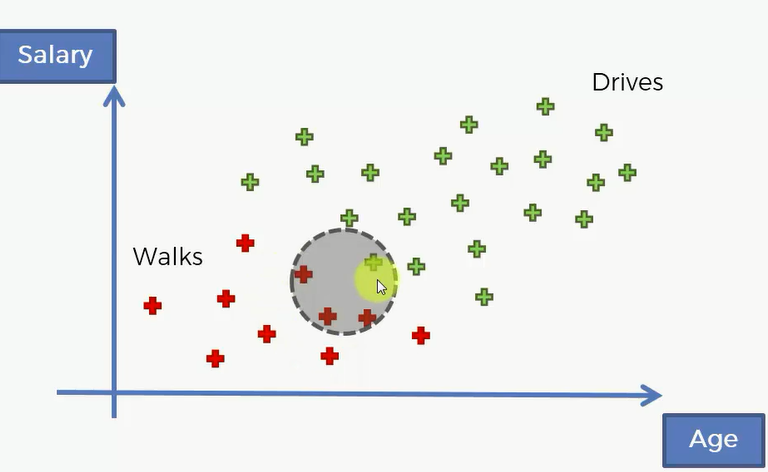
再然后求P(X}Walks),也就是边际似然,那么就是如果一个人是步行上班,那么它坐落在这个圈中的概率。P(X|Walks) = Number of Similar Observations Among those who Walk / Total number of Walkers = 3/10
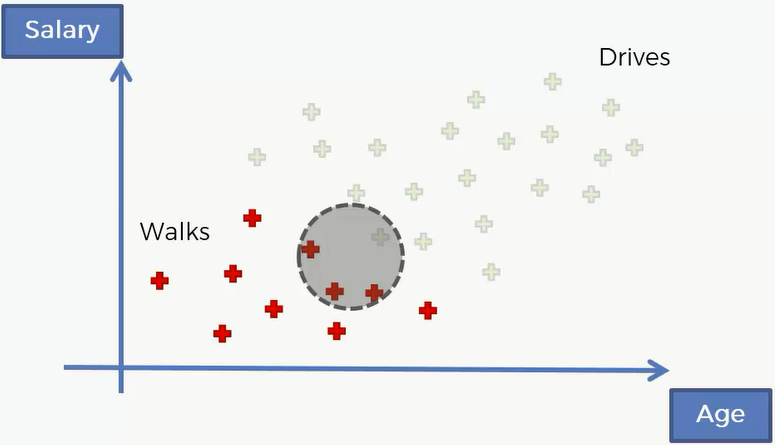
根据上面几个数据,我们可以计算出 P(Walks|X)
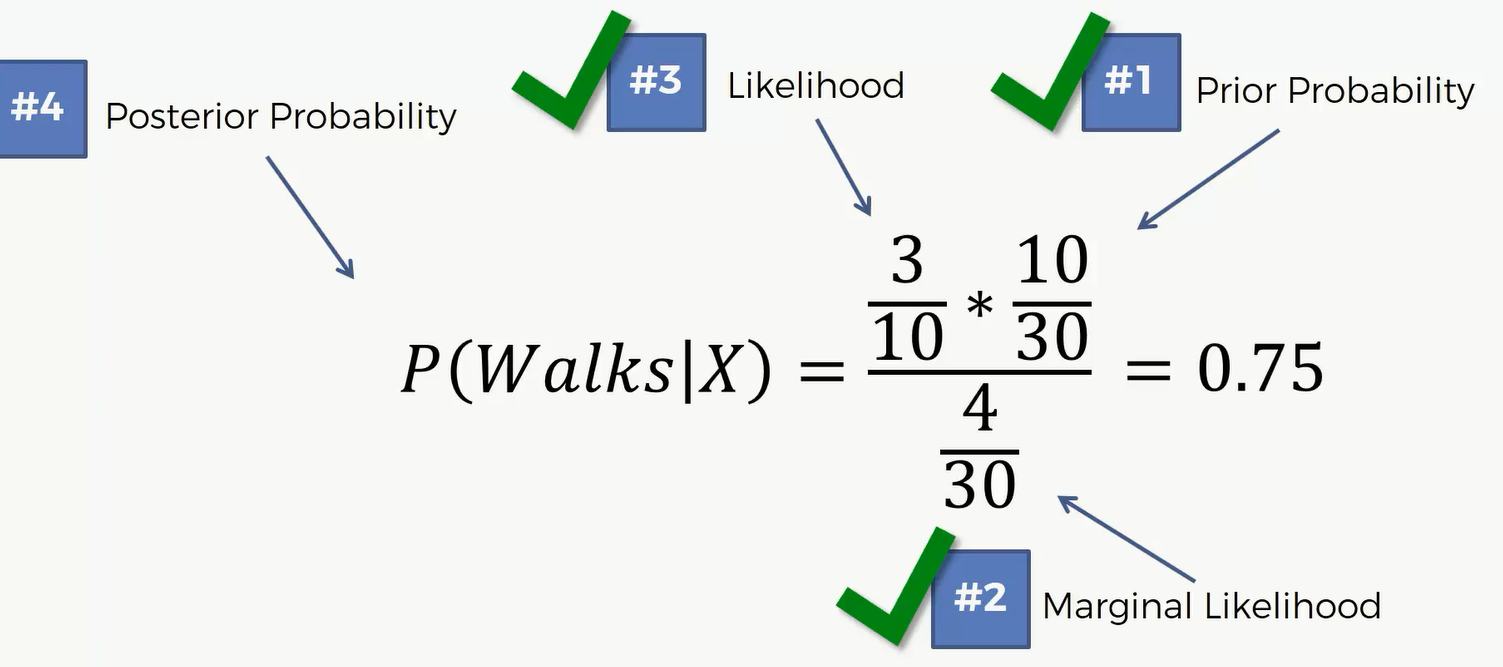
同理,我们可以得出 P(Drives|X) = 0.25
因为 0.75 > 0.25 所以这一点应该被划分到红色,也就是走路的一边去
朴素贝叶斯的一些补充说明
接下来我们来看看几个问题,首先第一个,为什么把它做朴素贝叶斯?或者为什么朴素?当我们使用朴素贝叶斯方法的时候已经做过一个假设,这个假设就是数据的所有特征都是独立的。在上述的例子里的两个特征,年龄和薪水,实际上这两者是可能有关系的,一般来说年龄越大可能薪水就越大。但这里假设年龄和薪水两者没有相关性。因此在一个机器学习的问题中,我们经常会做一些假设,这些假设并不一定都是对的,但这些假设可以帮助我们更高效快捷的解决问题。我们允许有一点误差,因为我们的终极问题是解决问题。
第二个问题,似然函数P(X),上面计算这个函数的方法是先在新数据周围画了个圈,表示在这个圈里的数据点,都表示和这个新数据点有相似的特征,那么接下来这个似然就是指如果有一个新的点,那么它坐落在这个圈中的概率。那么这个P(X)你会发现,它跟我们想要计算的后验概率是和红组相关还是绿组相关是没有关系的。我们最后要计算的两个后验概率的公式中的分母都是P(X),那么我们比较这两者实际上可以把这个P(X)个消掉,也就是说可以直接比较两者的分子P(X|Walks)*P(Walks)和P(X|Drives)*P(Drives)。
最后一个问题,若我们已知的组超过两组怎么办?目前已经有两组的情况下,比较两者的后验概率,那么我们将新数据分配到更大的概率的分组中。那么同理如果有三组的话,就是比较三者的后验概率,哪个更大就分配到其分组中。
代码
Importing the libraries
1 | import numpy as np |
Importing the dataset
1 | dataset = pd.read_csv('Social_Network_Ads.csv') |
Splitting the dataset into the Training set and Test set
1 | from sklearn.model_selection import train_test_split |
Feature Scaling
1 | from sklearn.preprocessing import StandardScaler |
Training the Naive Bayes model on the Training set
1 | from sklearn.naive_bayes import GaussianNB |
Predicting the Test set results
1 | y_pred = classifier.predict(X_test) |
Making the Confusion Matrix
1 | from sklearn.metrics import confusion_matrix, accuracy_score |
1 | [[65 3] |
Visualising the Training set results
1 | from matplotlib.colors import ListedColormap |
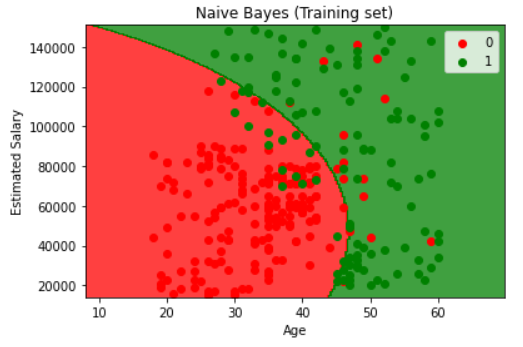
1 | from matplotlib.colors import ListedColormap |