K-Means聚类
首先我们要来看聚类(clustering) 和 分类(classification) 的区别:
参考博客: https://blog.csdn.net/gdp12315_gu/article/details/49777797
https://www.jianshu.com/p/1e7ddfddf14a
聚类:
将物理或抽象对象的集合分成由类似的对象组成的多个类的过程被称为聚类。聚类分析的一般做法是,先确定聚类统计量,然后利用统计量对样品或者变量进行聚类。对N个样品进行聚类的方法称为Q型聚类,常用的统计量称为“距离”;对于m个变量进行聚类的方法称为R型聚类,常用的统计量称为“相似系数”。
| Method name | Parameters | Scalability | Use case | Geometry (metric used) |
|---|---|---|---|---|
| K-Means | number of clusters | Very large n_samples, medium n_clusters with MiniBatch code |
General-purpose, even cluster size, flat geometry, not too many clusters | Distances between points |
| Affinity propagation | damping, sample preference | Not scalable with n_samples | Many clusters, uneven cluster size, non-flat geometry | Graph distance (e.g. nearest-neighbor graph) |
| Mean-shift | bandwidth | Not scalable with n_samples |
Many clusters, uneven cluster size, non-flat geometry | Distances between points |
| Spectral clustering | number of clusters | Medium n_samples, small n_clusters |
Few clusters, even cluster size, non-flat geometry | Graph distance (e.g. nearest-neighbor graph) |
| Ward hierarchical clustering | number of clusters or distance threshold | Large n_samples and n_clusters |
Many clusters, possibly connectivity constraints | Distances between points |
| Agglomerative clustering | number of clusters or distance threshold, linkage type, distance | Large n_samples and n_clusters |
Many clusters, possibly connectivity constraints, non Euclidean distances | Any pairwise distance |
| DBSCAN | neighborhood size | Very large n_samples, medium n_clusters |
Non-flat geometry, uneven cluster sizes | Distances between nearest points |
| OPTICS | minimum cluster membership | Very large n_samples, large n_clusters |
Non-flat geometry, uneven cluster sizes, variable cluster density | Distances between points |
| Gaussian mixtures | many | Not scalable | Flat geometry, good for density estimation | Mahalanobis distances to centers |
| Birch | branching factor, threshold, optional global clusterer. | Large n_clusters and n_samples |
Large dataset, outlier removal, data reduction. | Euclidean distance between points |
分类(Classification):
在已有分类标准下,对新数据进行划分,分类。
举例
假设有一批人的年龄的数据,大致知道其中有一堆少年儿童,一堆青年人,一堆老年人。
聚类就是自动发现这三堆数据,并把相似的数据聚合到同一堆中。所以对于这个例子,如果要聚成3堆的话,那么输入就是一堆年龄数据,注意,此时的年龄数据并不带有类标号,也就是说我只知道里面大致有三堆人,至于谁是哪一堆,现在是不知道的,而输出就是每个数据所属的类标号,聚类完成之后,就知道谁和谁是一堆了。
分类就是,我事先告诉你,少年儿童、青年人及老年人的年龄是什么样的,现在新来了一个年龄,输出它的类标号,就是它是属于少年儿童、青年人、老年人的哪个类。一般来说,分类器是需要训练的,也就是要告诉你的算法,每个类的特征是什么样子,它才能识别新的数据。
刚才举的是一个超级简单的例子,方便大家理解。下面再举一个实际的例子。
对于聚类,比如有些搜索引擎有“查看相似网页”的功能,这个就可以用聚类来做,把网页就行聚类,在聚类的结果中,每一个类中的网页看成是相似的。
对于分类,比如手写识别就可以看到是分类问题,比如我写了10个“我”字,然后对这10个“我”字进行特征提取,就可以告诉算法,“我”字具有什么样的特征,于是来了一个新的“我”字,虽然笔画和之前的10个“我”字不完全一样,但是特征高度相似,于是就把这个手写的字分类到“我”这个类,就识别出来了。
K-Means 聚类算法
对于这样一个二维数据集,我们可以对其进行 K-Means 聚类,结果就是原数据集被分成3类:
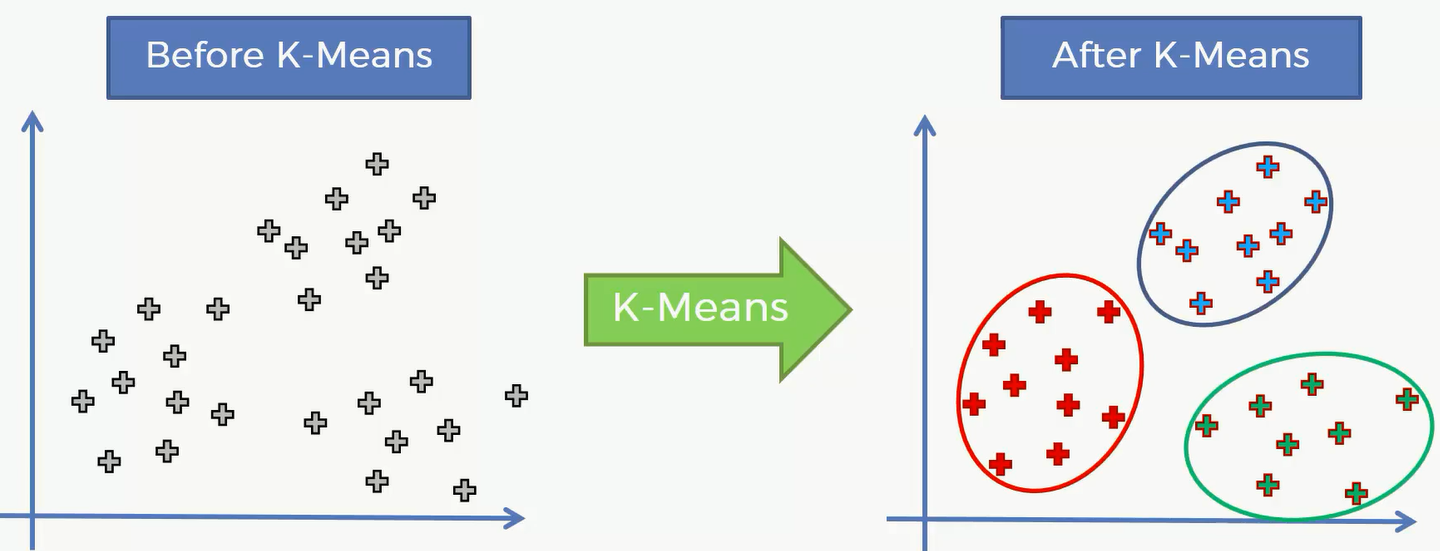
但是二维只是为了比较直观的展现K-Means 的功能,数据集可能是更高维度的,我们现在来看看K-Means 的内部逻辑
- 选择我们想要的类的个数K;
- 在平面上随机选择K个点,作为初始化类的中心点,不一定在原先数据当中;
- 对于数据集中的每个点,要判断它属于我们之前K个中心点的哪一类。依据数据中的每个点对这K个点的距离的大小,找到最短的距离,那么就是每个数据点对应的类别,这一步可以称作是分配;
- 重新计算一些新的中心点,就是应用之前分配的结果重新计算分配好的每个类当中的中心点;
重新分配,如果重新分配的结果和之前分配的结果相同,则说明找到最佳的K-Means算法的结果,如果不同,那继续去第四步进行分配计算,直到找到最佳算法结果

接下来我们具体拿一个例子来说明这些过程:

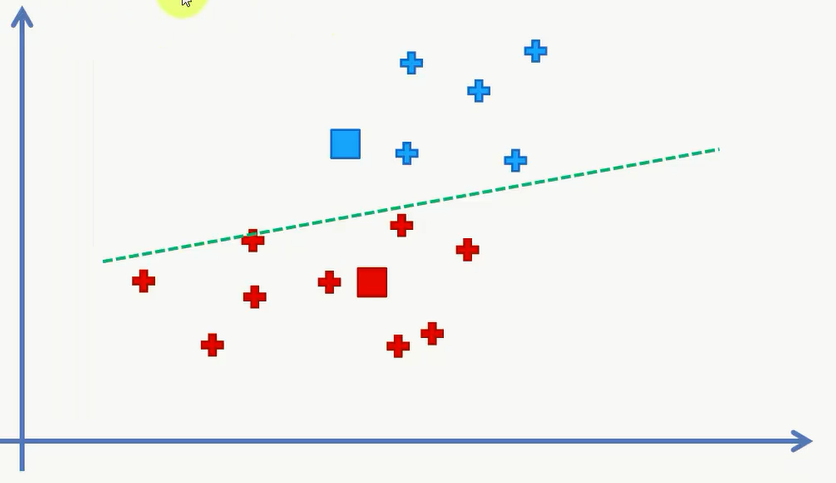
接下来我们要随机选择K=2 个点作为中心,并分别计算每个点距离这两个点的距离并进行分类。这里可以有个比较简单的计算方式,我们作出这两个点的垂直平分线,那么这个绿线上方的点都是离蓝色点比较近,下面的离红色比较近。
经过第一次分类,我们得到的分类如下:
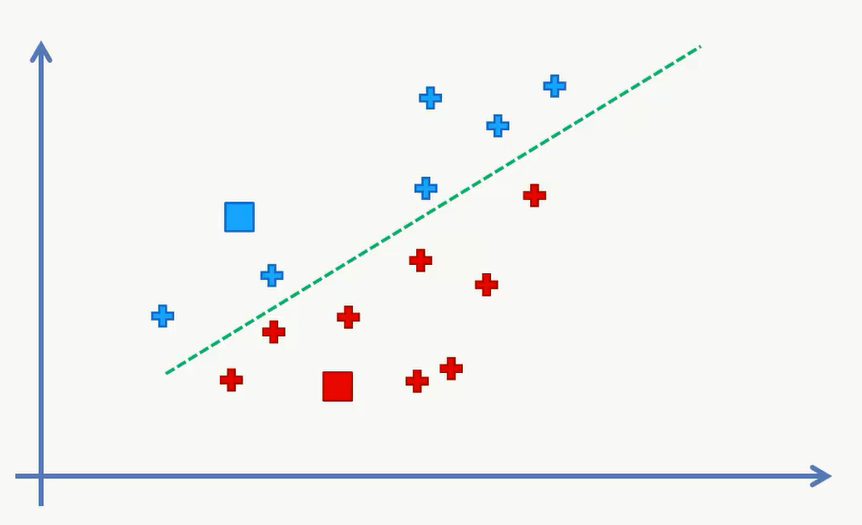
然后我们要计算一些新的中心点,也就是分配好的每个类当中的中心点。找到中心点之后我们又可以去重新分配数据。一直到重新分配的结果和未分配的结果相同时,完成聚类。
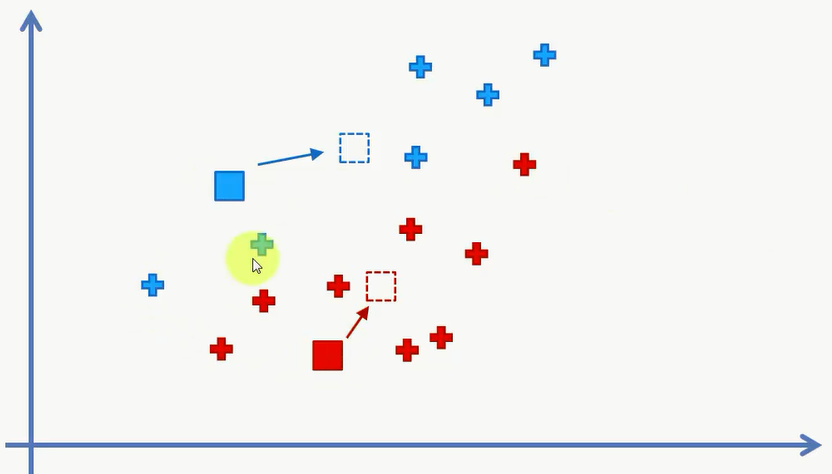
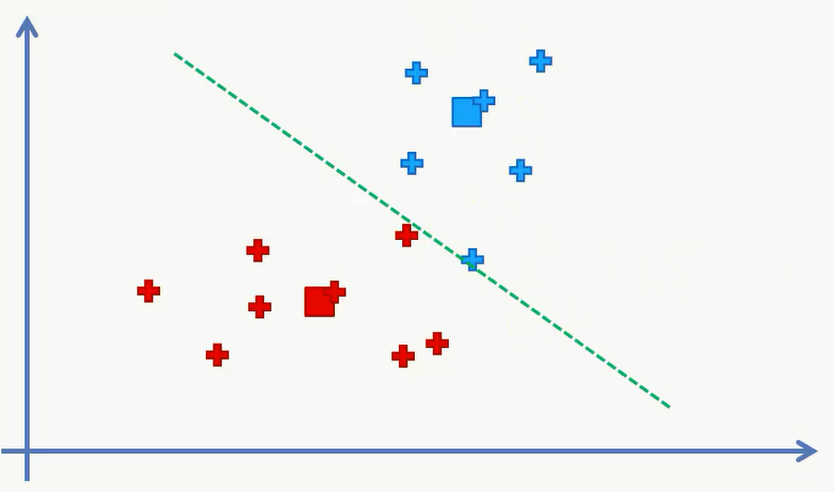
再次分类之后,我们得到:
对中心点进行更新:
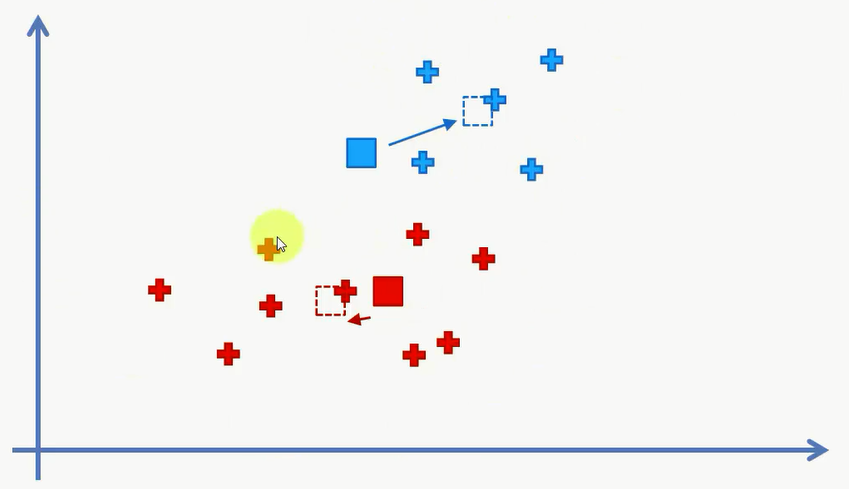
对数据进行分配:
对中心点进行更新:
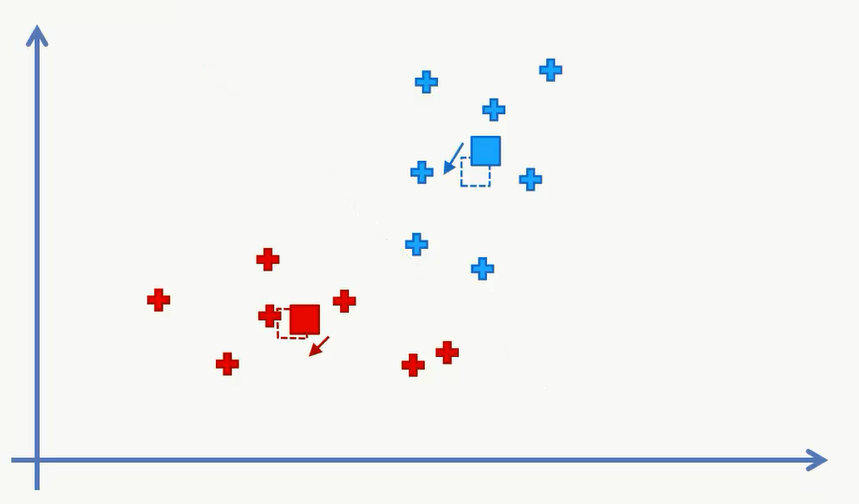
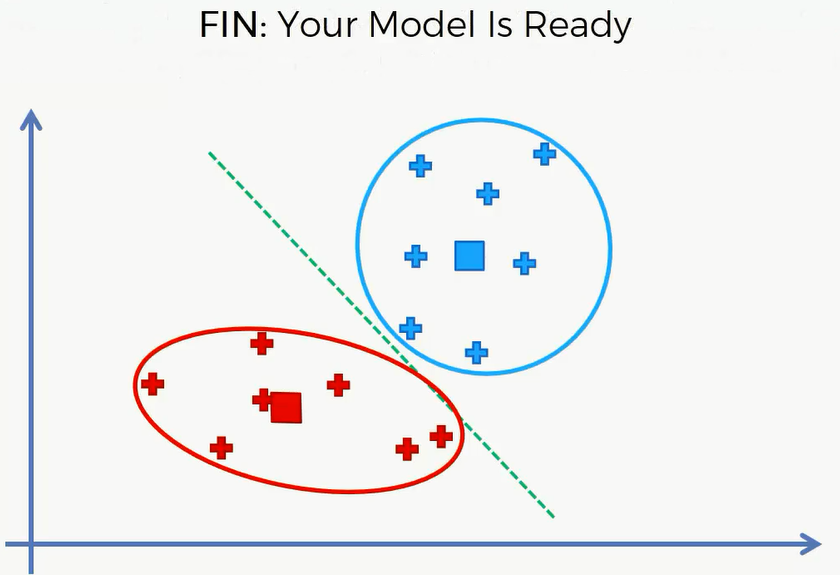
对数据进行分类,发现和之前的一样,说明聚类已经完成了:
随机初始化陷阱
现在看看初始点的选择对最终K-Means聚类结果的影响。下面有一个例子,我们需要用K-Means算法对这组数据进行聚类,选择K=3。这里很明显有三类,我们这里就直接选择最佳的中心点并标记出这三类数据。
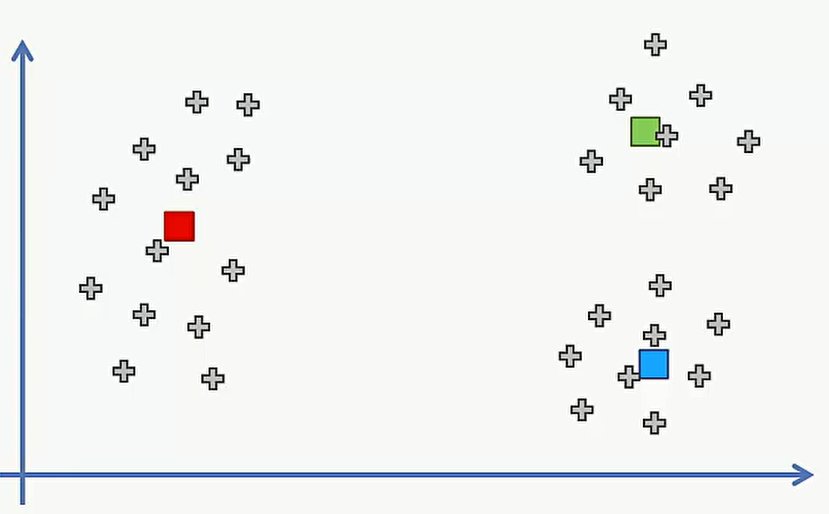
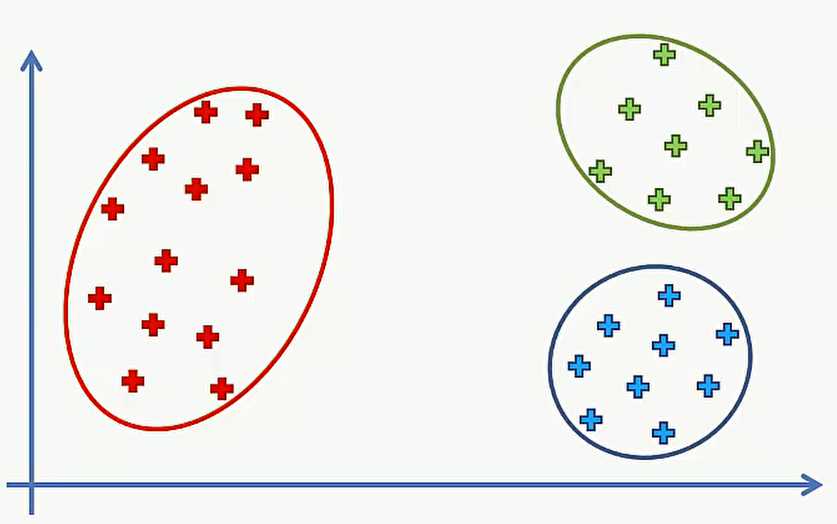
但是这里是我们肉眼看出来的三个中心点,但如果我们选择的不是最佳的中心点,则需要重复上述的45步,比如选的是下面这三个中心点。
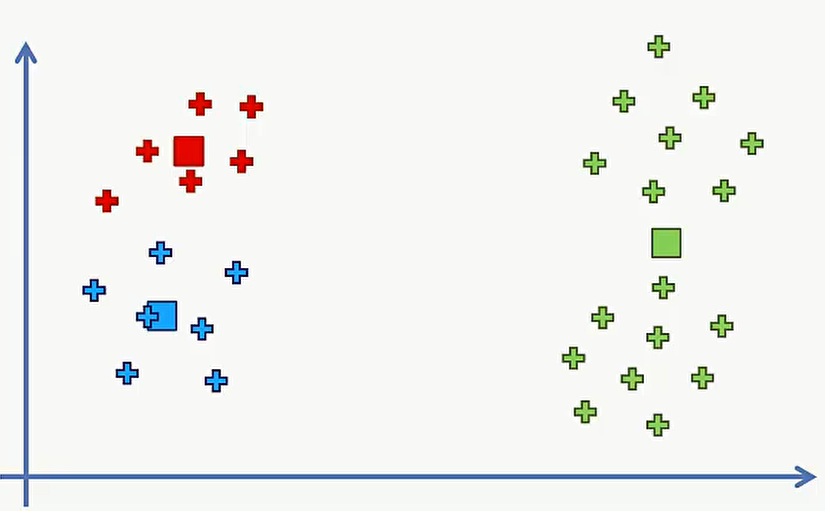
这样得到的分类结果和之前那个显然是不同的。但这样就发生了同一组数据,却产生了两个不同的分类结果。区别就在于选择了不同的初始中心点。我们不好直接说哪一个分类算法更好,需要有一个方法来判断如何选择初始中心点。也就是说初始中心点不能随机进行选择了。现在有一个K-Means算法的更新版本,叫做K-Means++,它完美的解决了初始化中心点的陷阱,数学上来讲叫做局部最小值的一个陷阱。无论在R还是Python中,这个K-Means++都已经加入了算法当中,因此不用担心之后的代码实现会不会掉入这个陷阱。
代码:
Selecting The Number Of Cluster
上文讲到的是选择中心点的陷阱,那么现在在谈谈如何选择类的个数。从直观上,上文中的图像大部分人应该很容易想到分为3组,也有的人可能想分为2组,但怎样选择才是最佳的分组方式是个需要好好研究的问题。首先来定义一个数学的量,组内平方和(WCSS)。

来看这个表达式,一共有3项,每一项代表对于每一组的平方和。比如第一项,就是对所有数据点对这一组中心点距离的平方。很显然,如果每一组的数据蜷缩的越紧,那么这个平方和就越小。
那么如果将这组数据分为1组,那么这个组内平方和只有一项,那么这个结果很显然会很大。如果分为2组,那么结果比1组的肯定要小,当分为3组时,得到的结果会更小。也就是说,随着分组的个数增加,这个组内平方和会逐渐变小。那么现在的问题来了,如何选择最合适的分组的个数?
这里要介绍一个法则,叫做手肘法则(The Elbow Method)。我们把随着分组个数的增加,WCSS的结果的图像画出来
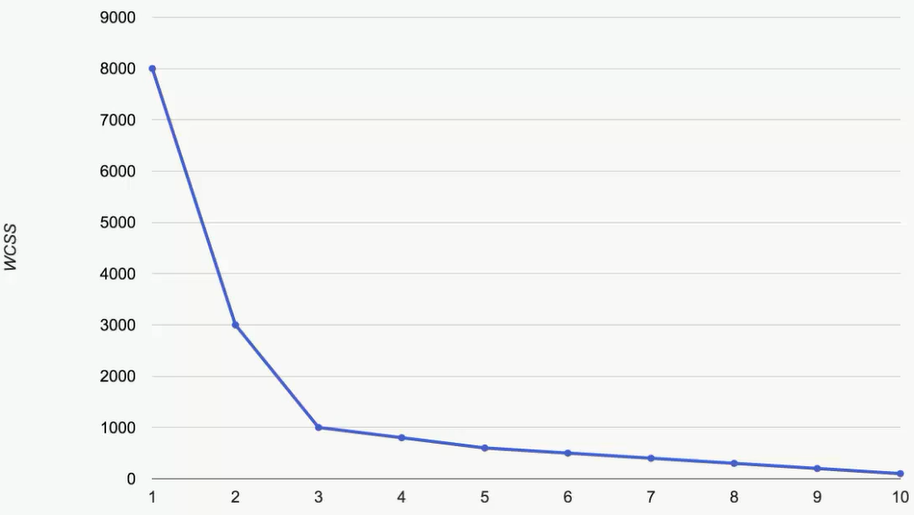
找到最像手肘的这个点,这里就是3,那么这个点,就是最佳的分组的个数。这个曲线上可以看到,从1到2,和2到3时,下降的速率都是比较快的,但从3往后,下降的速率都是非常小的,那么我们要找的就是这样一个点,在到达这个点之前和从这个点开始的下降,速率的变化时最大的。
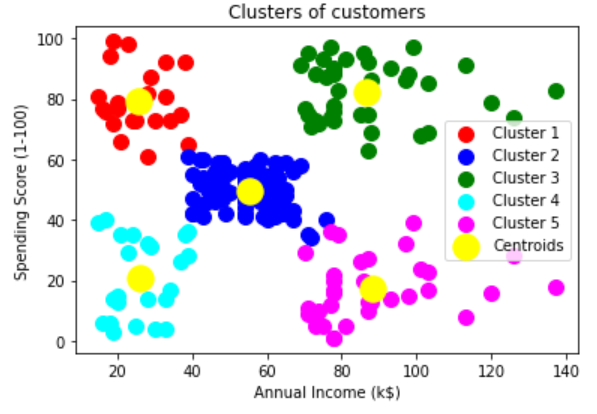
Clustering
我们这次要用到的数据集部分如下,反映的是一个购物商场的购物信息。最后一列Spending Score是购物商场根据客户的信息打出的客户的评分,分数越低意味着客户花的钱越少,越高以为着客户花的越多。商场希望通过对客户的年收入和购物指数来进行分群
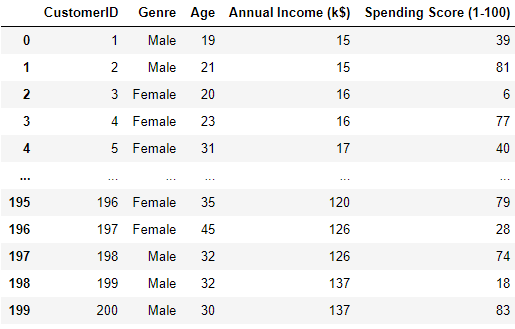
首先我们进行导库和导数据集
1 | import numpy as np |
Using the elbow method to find the optimal number of clusters
那么这个问题的自变量就是第四五列,年收入和购物指数。但它是个无监督学习,因此没有因变量。我们要将其最终分为几类。这里我们要用到的工具是sklearn.cluster中的KMeans类。首先要计算各个分组的WCSS。这里我们计算组数从1到10的情况。
1 | from sklearn.cluster import KMeans |
这里的KMeans中的参数也解释下,n_clusters指的是分组数,max_iter指的是每一次计算时最大的循环个数,这里使用默认值300,n_init代表每一个做K平均算法时,会对多少组不同的中心值进行计算。init这个参数非常重要,指的是我们如何选择初始值,最简单的是random,即随机,但为了避免掉入随机初始值陷阱,这里使用k-means++。
拟合好后得到组间距离就是kmeans.inertia_。这样我们就可以画出对于不同的分组数,wcss的图像。
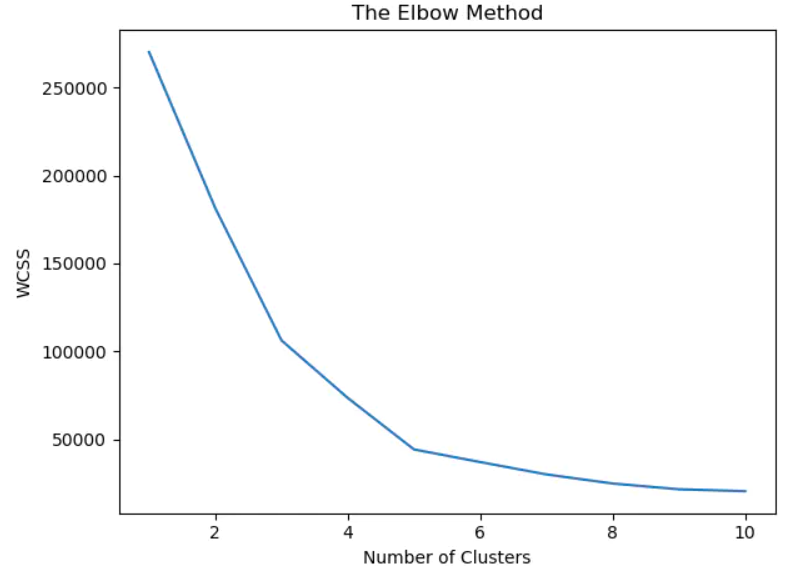
那么通过手肘法则,可以得到最佳的分组个数是5组,则可以开始拟合数据。
Training the K-Means model on the dataset
1 | kmeans = KMeans(n_clusters = 5, init = 'k-means++', random_state = 42) |
Visualizing the clusters
1 | plt.scatter(X[y_kmeans == 0, 0], |