Upper_Confidence_bound

Posted on
Words count in article: 2.9k | Reading time ≈ 10

Upper Confidence bound

搬运、修改自 博客https://www.jianshu.com/p/3abeb6d4a1e5

引入：

如图所示，我们有几个单臂老虎机，组成一起我们就称作多臂老虎机，那么我们需要制定什么样的策略才能最大化得到的奖励。这里假设每个老虎机奖励的随机分布是不一样的。

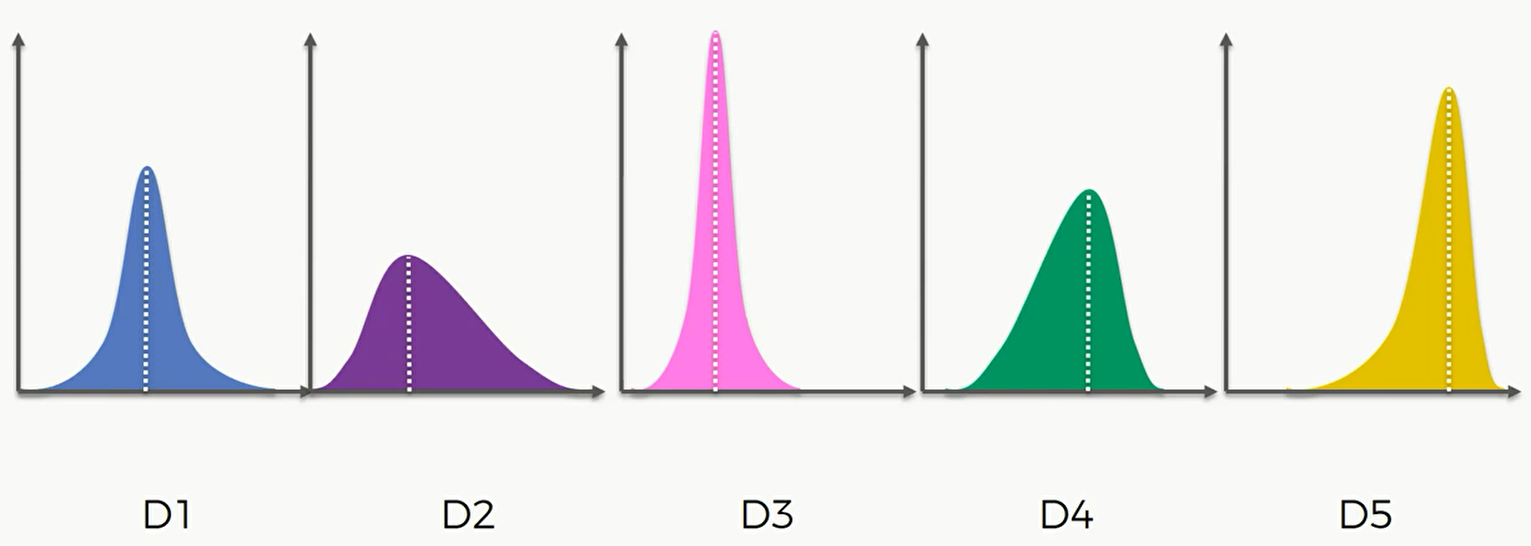
比如第一个分布，D1这个老虎机的分布大概率落在中间这部分，很小概率在两头的地方。假设用户是知道这些分布的，那么用户应当怎么选择？答案很简单，我们应当选择D5这个老虎机，因为它的平均值最高，而且有很大概率在靠右也就是正数范围内。但现在的问题是，用户实际上是不知道这些老虎机的概率分布的。那么我们需要一次次的尝试，尽可能快速的找到这五个老虎机的分布，并利用最佳的分布最大化收益。这个在机器学习上叫做，探索利用。

探索和利用这两步实际上并不是那么的兼容，为了解释这个概念，这里引入一个定义，叫做遗憾。也就是我们知道D5的分布是最高的，那么最佳策略是应对不停的选择D5这个机器，但当我们不知道的时候，可能会选择其他的机器，当没有选择最佳机器时，都会得到一个得到的奖励和最佳奖励的差，这个差就是遗憾。

那么现在可以解释为什么探索和利用为什么并不是那么兼容，比如我们探索很多，每个机器玩了一百次，对于每个机器都能得到很好的分布估计，但同时也会带来很多的遗憾。如果探索比较少，可能会找不到最佳的分布，探索得到的结论可能是错的。所以说，最佳的策略应该是，通过探索找到最佳分布的老虎机，并且以一种快速而高效的方法找到这个老虎机，且不断的利用它来获得最大化的奖励。

在实际上生活或商业案例上也有很多相似的情形。比如可口可乐公司设计出了5个不同的广告，那么现在的问题就是不知道哪个广告是最好的，能带来最佳的用户转换率，即不知道哪一个投放后会吸引用户点击或购买产品。非常传统的方式就是把每个广告都投放到市场上几天，然后看看得到的结果。但这是很消耗人力和财力的，而且这本质上只进行了探索却没进行利用。因此我们需要对此进行利用，比如其中某个广告投放第一天就显然没有任何的效果，那么后面几天的投放的意义就不是很大了，可以考虑不再投放此广告来节省人力财力。即应用强化学习可以优化成本和支出，又可以得到最高的收益。

置信区间上界算法

下面来描述下这个算法,现在假设我们知道五台老虎机的分布，那么我们会不断的选择D5这个老虎机。假如说不知道这几个的概率分布，那么就要开始我们的算法。

1

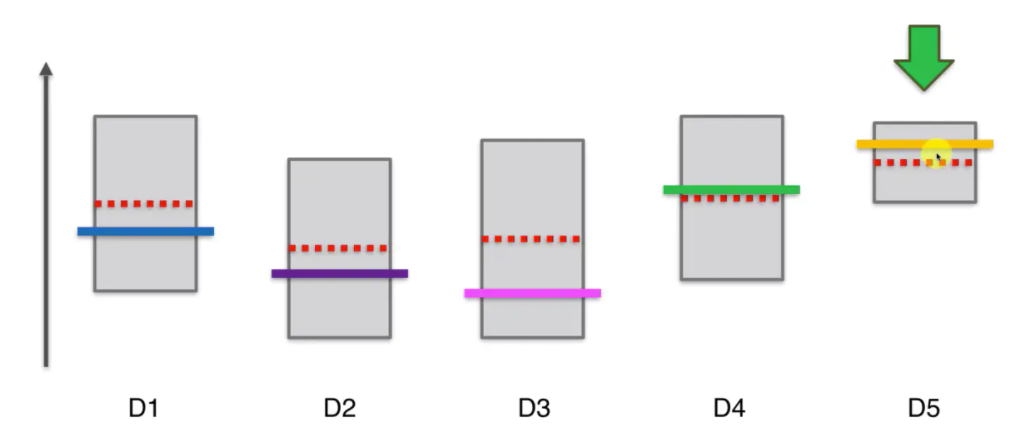
在我们开始之前，假设每个老虎机的概率分布是相同的，即平均值或期望是相同的。如图红色虚线表示平均值或期望，纵轴表示老虎机可能带来的收益。这些彩色的横线代表每个老虎机实际的平均或期望，这些期望我们是不知道的，这个问题的核心就是我们要进行不断的尝试去估算出每个老虎机的平均期望。

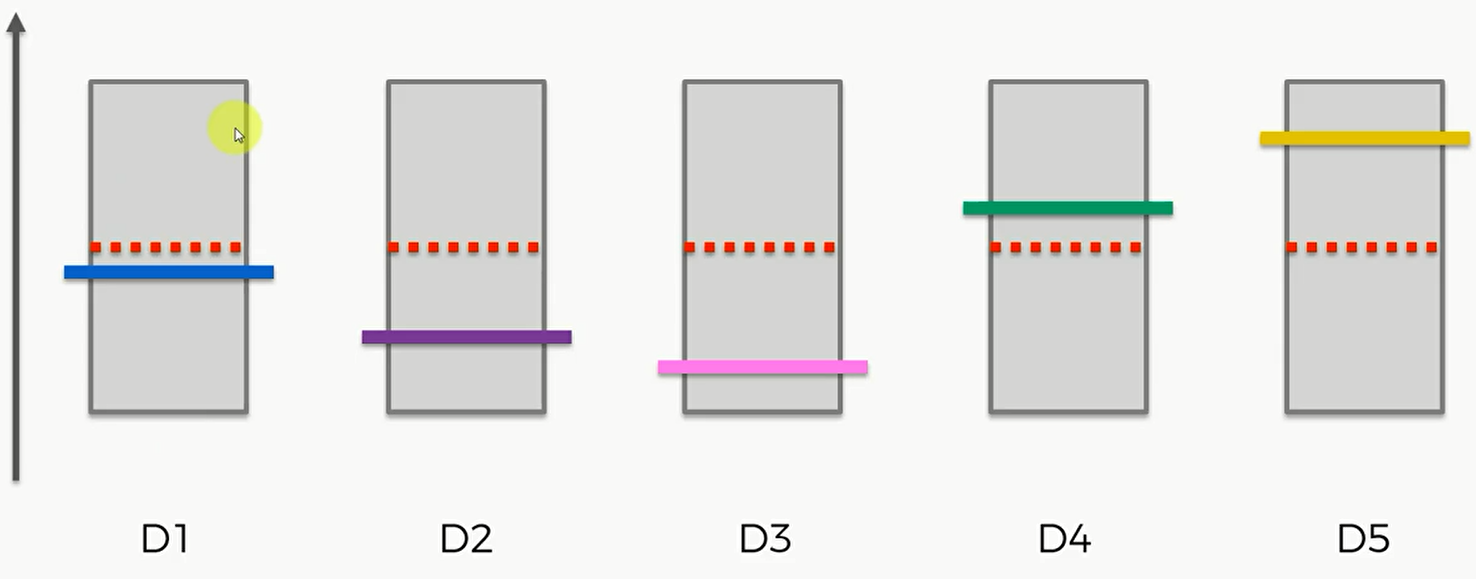
置信区间，Confidence Bound 对于每个老虎机，我们讲置信区间，用灰色的方框表示。对于每个老虎机，我们按的概率有很大的概率是在这个区间当中的。我们每一轮将要选择的就是拥有最大的区间上界的老虎机，也就是顶上的这条线最大的老虎机，我们要在每一轮中选择它并按下它。在第一轮中，他们的区间上界是一样的。

2

现在，比如选择3号老虎机，按下去，首先会发现区间所代表的方框下降了。因为按下去后我们会发现其给予的奖励，3号老虎机的实际期望比较低，那么观察得到的奖励也是比较低，那么重新计算观察到的所有平均值时，那么这个平均值就降低了。第二点，我们会发现这个置信区间变得更小了，因为比起上一轮的游戏，我们总共的观察次数变多了，也就是信心升高了，那么这个置信区间的长度就会变小。

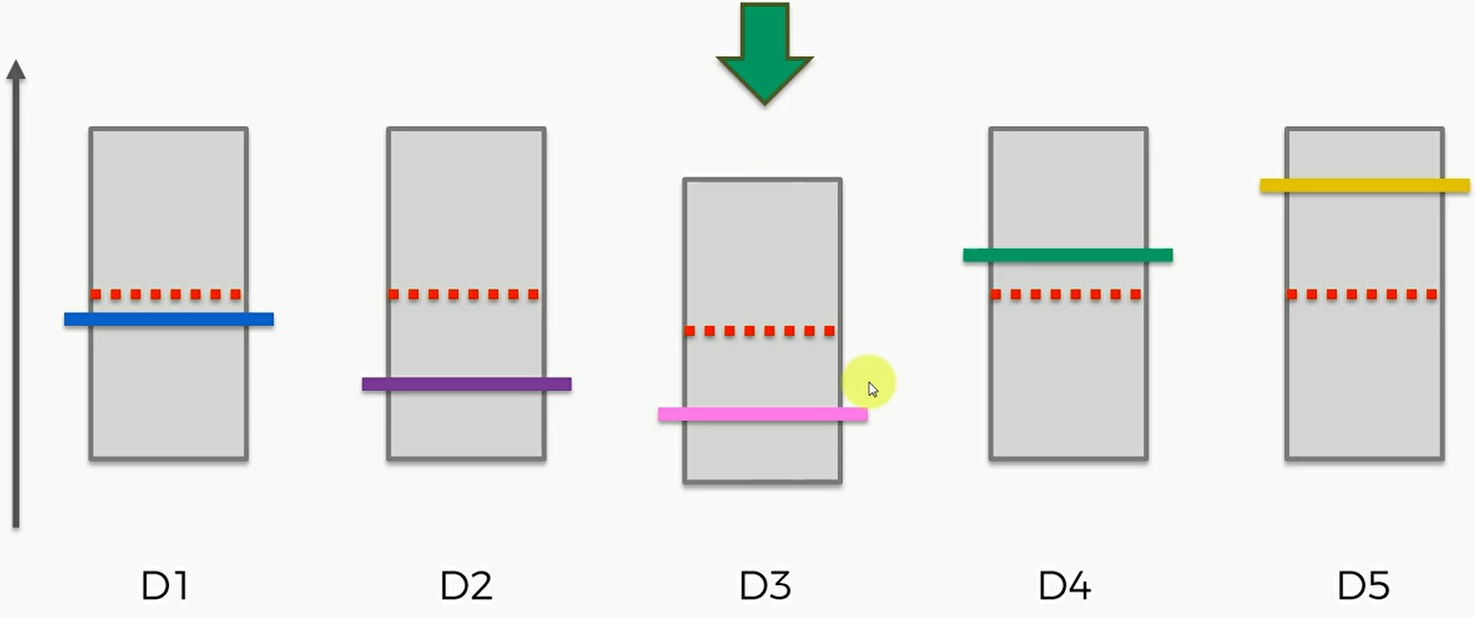
3

那么此时第三个机器的置信区间上界比其他的要低，所以下一轮要选择其他四个机器，比如选择第四个，那么它的置信区间上界会变高，区间大小会变小。

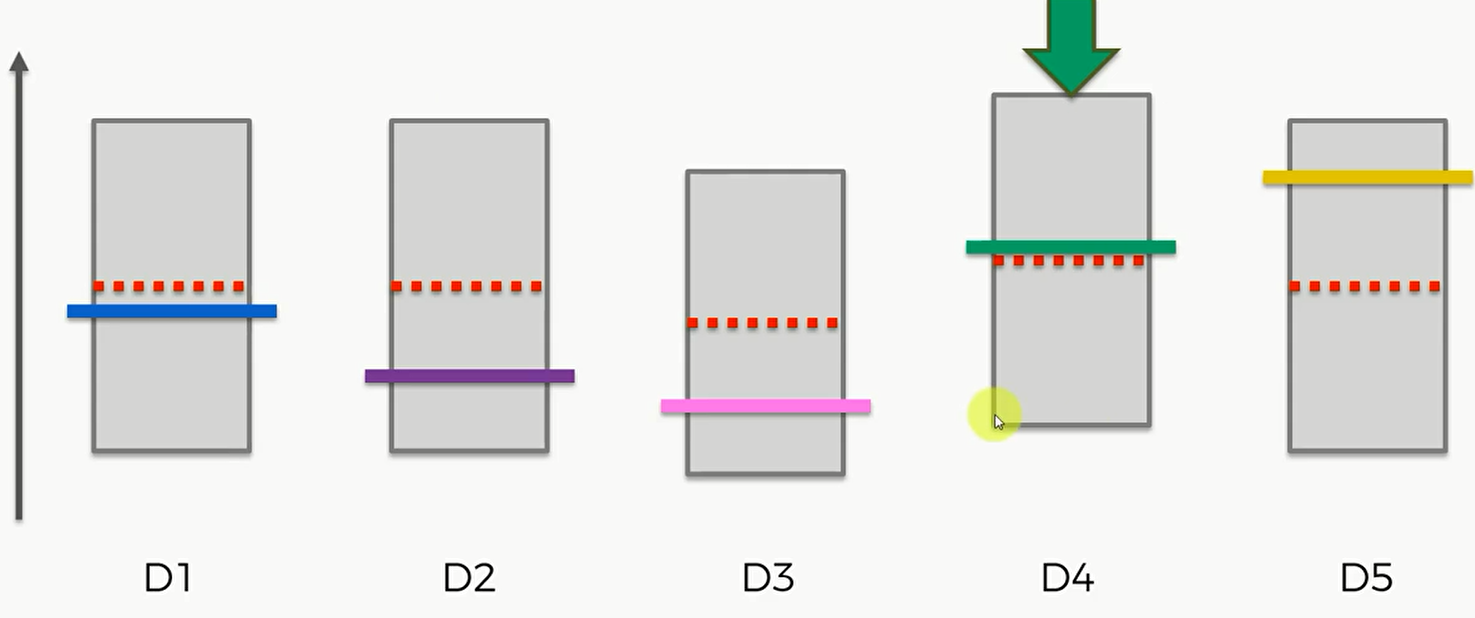
但是这样的话，D4的置信区间上界就高于其他所有机子。如果这是最后一次迭代的话，我们的算法就会认为D4十表现最好的机子。但是这显然并不符合实际。那么这个算法的意义就丧失了。

但是不要忘记，UCB的置信区间是 $[\overline r_i(n)-\Delta_i(n),\overline r_i(n)+\Delta_i(n)]$ 其中 $\Delta_i(n) = \sqrt{\frac{3}{2}\cdot \frac{\log(n)}{N_i(n)}}$ ，$N_i$ 随着轮数增加会增加，所以 $\Delta_i$ 会减小，所以虽然 $\overline r_i(n)$ 增大了，但是置信区间却减少了，”资不抵债” ，最终它的置信空间上界还是变小了。

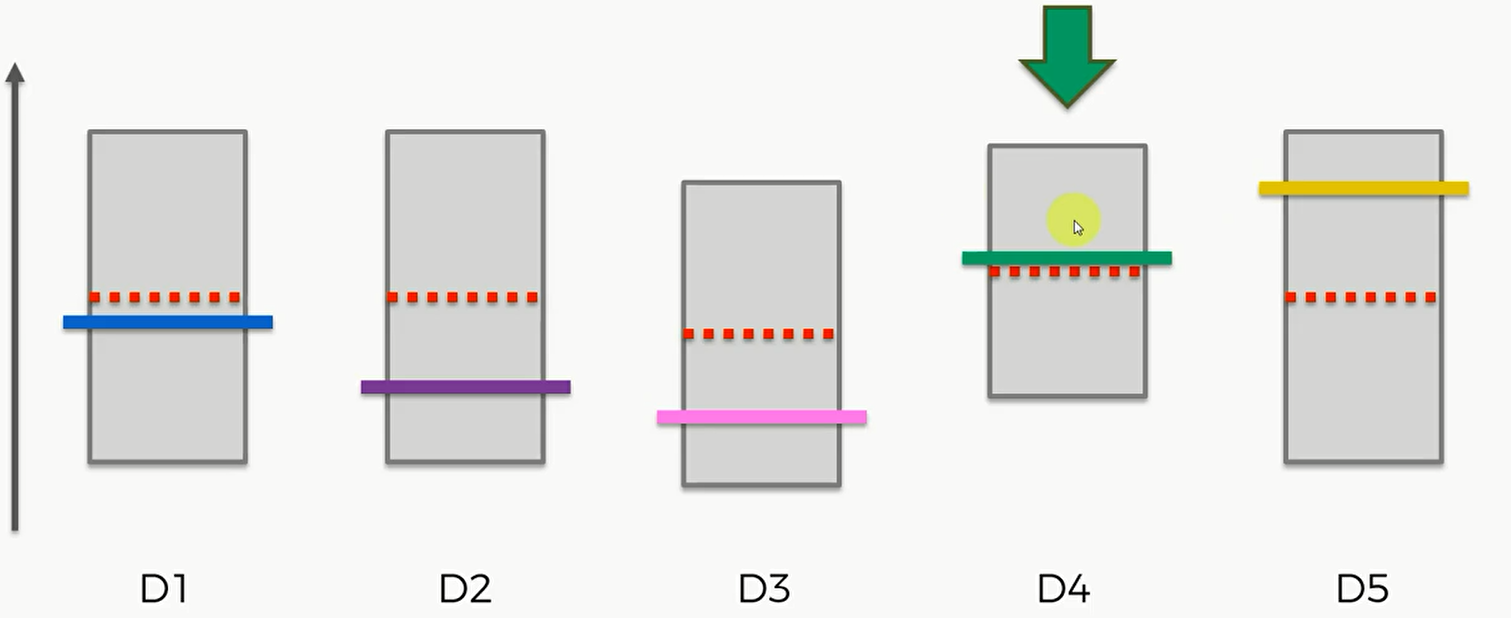
4

下一步，125三个机器的上界时一样的，因此可以在他们三个中间选一个，比如第一个，它的实际平均值比较低，但当我们按下老虎机的时候，它实际是个随机事件，因此可能高也可能低。虽然它的平均值，但假设此时运气比较好，投下去的钱翻倍了，那么他的区间上限变高，长度变小。

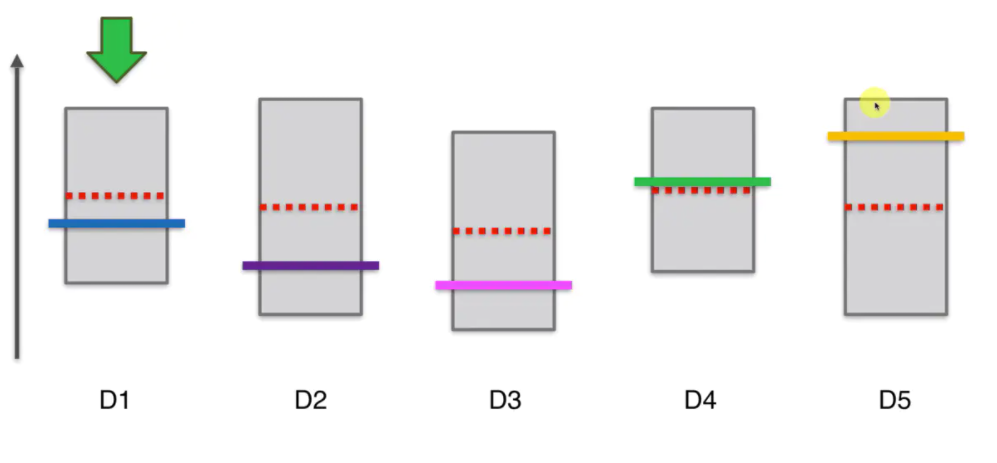
再然后在25中间选择一个，比如第二个，此时他的置信区间上界变低，宽度变小。

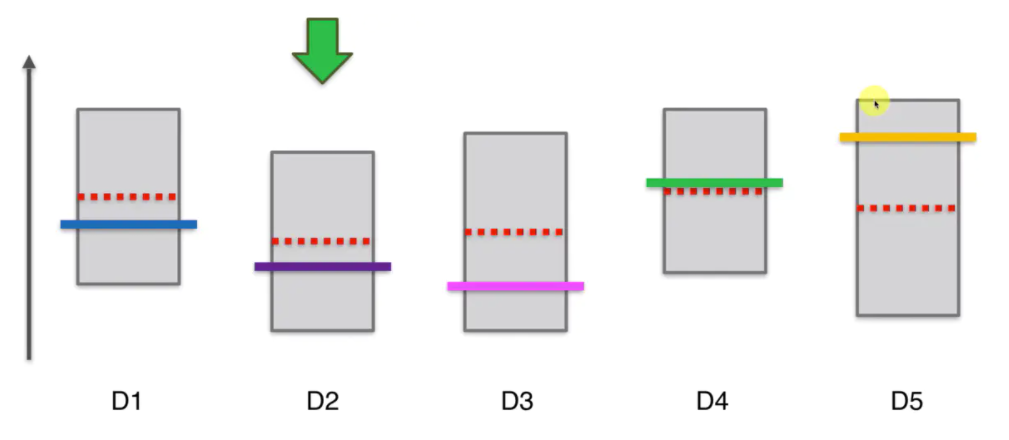
那么最后按下第五个机器，这时得到一个非常高的观察值，那么上限变高，宽度变小。但由于D5实际上是最佳的机器，那么就算置信区间变小了，但它的上界依然比其他的都要高。

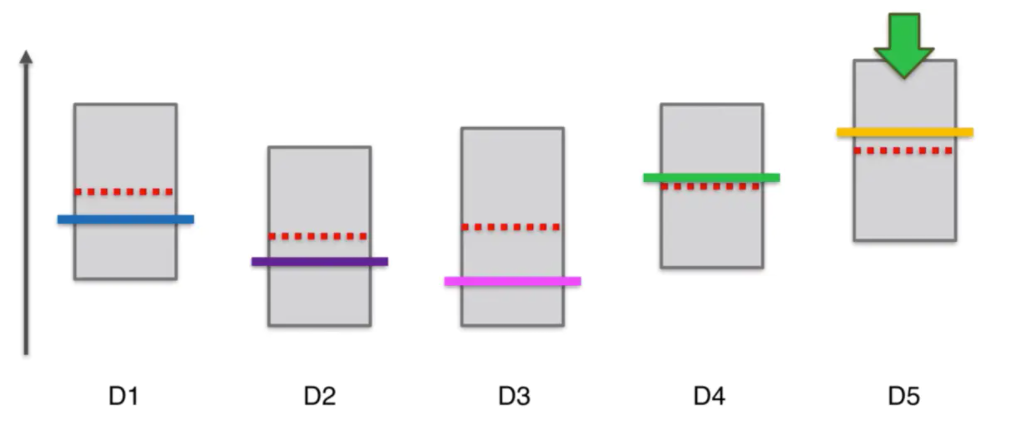
5

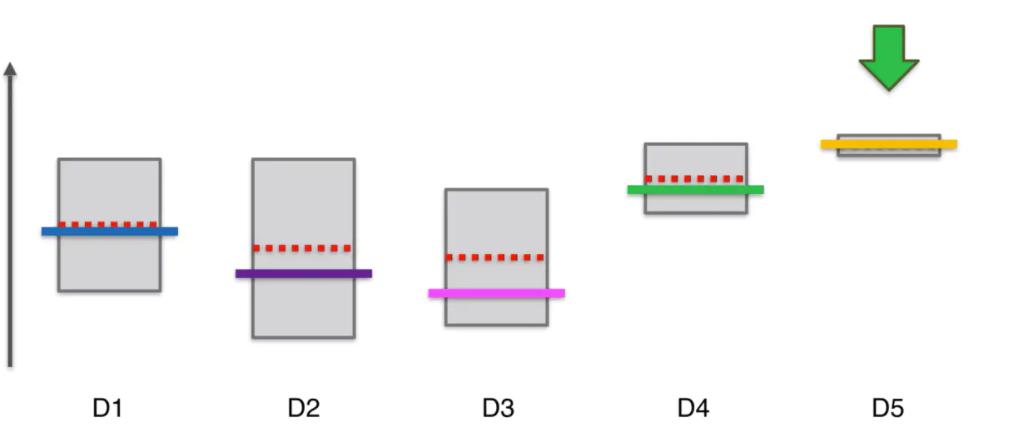
那么我接下来选择的老虎机依然是它，当我们选择了一个最佳的解时，我们可能在这个选择上停留很多轮，但由于对他的信心会越来越高，因此这个区间会越来越小，此时的区间上界可能就会变成不是最高。

UCB算法有一个特点，当我们选择了一个机器很多次后，他的置信区间会变得很小，要给其他的机器一些机会，看看其他机器显示的观察结果所对应的新的置信区间上界是否会更高。这样经过很多轮后，最终D5的选择次数依然会很多很多，他的置信区间会越来越扁，一直到最终轮。

代码实现

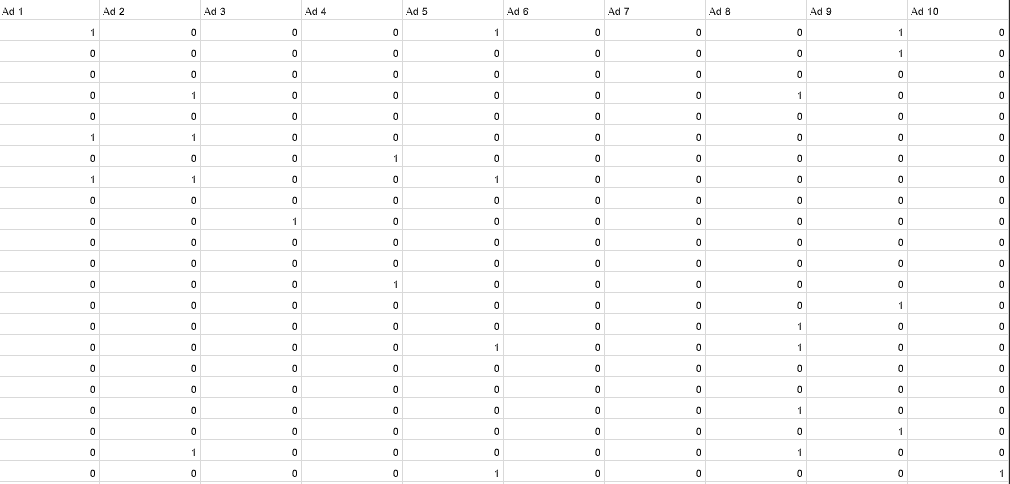
这里用一个商业案例来做例子。假设有一个汽车公司为了一个车做了十个广告ad1-ad10，这个公司需要知道哪个广告投放后，点击率最高。这组数据集是在模拟环境得到的，若值为1则指的是这个用户点击了这个广告。总结一下问题就是，我们有十个广告，要决定哪个广告有最高的点击率，并对逐步得到的信息来决定，第n个用户投放哪个广告得到最高的点击数。我们先看看如果对于每一个用户，我们随机抽选广告，会得到怎样的点击数。

我们要用的数据集如下：

这里提供一个随机选择的算法，不是此次算法的重点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# Importing the libraries
import matplotlib.pyplot as plt
import pandas as pd

# Importing the dataset
dataset = pd.read_csv('Ads_CTR_Optimisation.csv')

# Implementing Random Selection
import random
N = 10000
d = 10
ads_selected = []
total_reward = 0
for n in range(0, N):
    ad = random.randrange(d)
    ads_selected.append(ad)
    reward = dataset.values[n, ad]
    total_reward = total_reward + reward

# Visualising the results
plt.hist(ads_selected)
plt.title('Histogram of ads selections')
plt.xlabel('Ads')
plt.ylabel('Number of times each ad was selected')
plt.show()

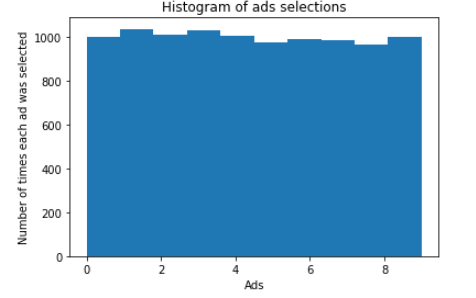
运行后得到的ads_selected代表对于每一个用户，哪一个广告被选择，total_reward指的是所有的点击数。得到的图像表示每个广告被点击的次数。每个广告的到点击次数是接近的，大致在1000左右。

这样，经过10000轮之后，最终得到的reward为 1257

Importing the libraries

1
2
3
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

Importing the dataset

1
dataset = pd.read_csv('Ads_CTR_Optimisation.csv')

Implementing UCB

对于UCB算法，我们没有直接的工具包来使用，因此需要自己实现，下面是算法逻辑：

首先我们设置 N (即用户的总数/运行轮数)，d是广告总数

numbers_of_selections 和 sums_of_rewards 分别是 $N_i(n)$ 和 $R_i(n)$ , [0]*d 即初始化一个长度为十，初始值都为0的列表

total_reward 是所有返回值的总和，当前没有任何奖励，所以设置其值为0

接着就是进行一个循环了，n代表轮数，在每一轮中，ad(这一轮选择的广告)设置为0(即从第一个广告开始），最大上界设为0

然后对于十只广告中的每一支，我们首先判断其被投放的次数是否大于0，若大于0则计算器 平均回报并计算其置信空间。如果不大于0，那么我们就先将其置信空间的上界设置为一个非常非常大的数。

如果得到的上界是大于最大的置信空间上界，那么就更新最大的置信空间上界，并将当前的广告赋给ad。即这个广告是这一轮我们要投放的广告。所以前两轮下来，最大上界肯定是1e400，但是第三轮之后，最大上界就在不断更新和改变。

跳出第二个循环，我们将本轮最终选的广告添加到ads_selected 列表当中去。并将这个广告的$N_i$ 加一。另外还要再dataset中查找这轮这条广告的reward并加到 $R_i$ 和total_reward 当中去

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import math
N = 10000
d = 10
ads_selected = []
numbers_of_selections = [0] * d
sums_of_rewards = [0] * d
total_reward = 0
for n in range(0, N):
    ad = 0
    max_upper_bound = 0
    for i in range(0, d):
        if (numbers_of_selections[i] > 0):
            average_reward = sums_of_rewards[i] / numbers_of_selections[i]
            delta_i = math.sqrt(3/2 * math.log(n + 1) / numbers_of_selections[i])
            upper_bound = average_reward + delta_i
        else:
            upper_bound = 1e400
        if upper_bound > max_upper_bound:
            max_upper_bound = upper_bound
            ad = i
    ads_selected.append(ad)
    numbers_of_selections[ad] = numbers_of_selections[ad] + 1
    reward = dataset.values[n, ad]
    sums_of_rewards[ad] = sums_of_rewards[ad] + reward
    total_reward = total_reward + reward

Visualizing the results

现在 ads_selected 数组是一个

1
2
3
4
5
plt.hist(ads_selected)
plt.title('Histogram of ads selections')
plt.xlabel('Ads')
plt.ylabel('Number of times each ad was selected')
plt.show()

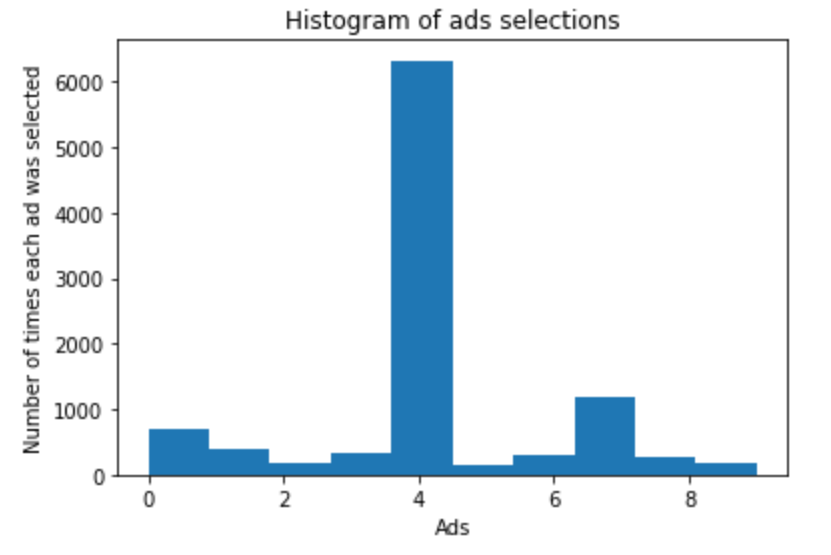
查看ads_selected会发现编号4出现的次数最多，即第五个广告ad5。经过10000轮之后，最终的reward值为2178。和上面的随机算法相比，reward提升了很多很多

-------------本文结束，感谢您的阅读-------------