线性代数之特征值与向量
概念与求法
概念
设A是n阶矩阵,如果数$\lambda$ 和n维非零向量x满足 $Ax=\lambda x$ 。则称$\lambda$ 是矩阵A的特征值。非零向量x称为矩阵A的对应于特征值 $\lambda$ 的特征向量。因为 $Ax=\lambda x$ 等价于 $Ax-\lambda x=0$ 或 $(A-\lambda E)x = 0$
如果 $\lambda$ 是矩阵A的特征值,则矩阵A的对应于(属于)特征值 $\lambda$ 的特征向量x是齐次线性方程组 $(A-\lambda E)x = 0$ 的非零解,且 $(A-\lambda E)x = 0$ 的解空间称为矩阵A对应于特征值 $\lambda$ 的特征空间
在复数范围内,我们有以下等价命题:设A是一个n阶矩阵,$\lambda$ 是一个数。则:
- $\lambda$ 是矩阵A的特征值
- 存在非零向量x,使得 $Ax=\lambda x$
- 齐次线性方程组 $(A-\lambda E)x=0$ 的非零解
- 行列式 $|A-\lambda E|=0$
求解矩阵A的特征值与特征向量的步骤
- 解特征方程 $|A-\lambda E|=0 $ 得到 n个特征值 $\lambda_1,\lambda_2,\cdots,\lambda_n$
- 对每个特征值 $\lambda_i$ ,解齐次线性方程组:$(A-\lambda_iE)x=0$ 。设 $\xi_1,\xi_2,\cdots,\xi_n$ 是此方程组的基础解系,则A属于特征值 $\lambda_i$ 的全部特征向量为 $p=k_1\xi_1+\cdots+k_l\xi_l$ (其中 $k_1,\cdots,k_l$ 不全为0)
我们用三个例子来具体阐释这些步骤:
第一个:$A=\begin{pmatrix} 3 & -1 \ -1 & 3 \end{pmatrix}$ 求这个矩阵的特征值和特征向量
解:A的特征方程 $|A-\lambda E|=0$
$|\begin{pmatrix} 3 & -1 \ -1 & 3 \end{pmatrix}-\begin{pmatrix} \lambda & 0 \ 0 & \lambda \end{pmatrix}|=|\begin{pmatrix} 3-\lambda & -1 \ -1 & 3-\lambda \end{pmatrix}|=(3-\lambda)^2-1$
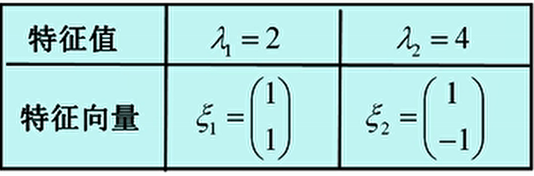
$=[(3-\lambda)+1][(3-\lambda)-1]=(4-\lambda)(2-\lambda)=0$ 解得 $\lambda_1=2,\lambda_2=4$
对$\lambda_1=2$ 对应的齐次线性方程组为 $(A-2E)x=0$
所以 $\begin{pmatrix} 3-2 & -1 \ -1 & 3-2 \end{pmatrix}\begin{pmatrix} x_1 \x_2 \end{pmatrix}=\begin{pmatrix} 0 \ 0 \end{pmatrix}$
$\begin{pmatrix} 1 & -1 \ -1 & 1 \end{pmatrix}\rightarrow \begin{pmatrix} 1 & -1 \ 0 & 0 \end{pmatrix}$(上一行加下一行)
于是我们得到 $x_1-x_2=0$, $x_1=x_2$ 不妨令 $x_2=1$,则得到基础解系 $\xi_1= \begin{pmatrix} 1 \ 1 \end{pmatrix}$ 则A对应于 $\lambda_1=2$ 的全部特征向量为 $p_1=k\begin{pmatrix} 1 \ 1 \end{pmatrix}$
对 $\lambda_2=4$ ,对应的齐次线性方程组为 :$(A-4E)x=0$
同理我们可以得到 $x_1=-x_2$ ,不妨令 $x_2=-1$ ,则得到的基础解系 $\xi_2= \begin{pmatrix} 1 \-1 \end{pmatrix}$,则A对应于 $\lambda_2=4$ 的全部特征向量为 $p_2=k\begin{pmatrix} 1 \ -1 \end{pmatrix}$
第二个 :$A=\begin{pmatrix} -2 & 1 & 1 \ 0 & 2 & 0 \ -4 & 1 & 3 \end{pmatrix}$ 求这个矩阵的特征值和特征向量
解:首先求A的特征方程 $|A-\lambda E|=0$
则 $\begin{vmatrix} -2-\lambda & 1 & 1 \ 0 & 2-\lambda & 0 \ -4 & 1 & 3-\lambda \end{vmatrix}=(2-\lambda)\begin{vmatrix} -2-\lambda & 1 \ -4 & 3-\lambda \end{vmatrix}=(2-\lambda)(-6-\lambda+\lambda^2+4)=(2-\lambda)(\lambda-2)(\lambda+1)=0$
解得 $\lambda_1=-1,\lambda_2=\lambda_3=2$
那么我们依次将这些特征值带入到方程中并求出特征值对应的特征向量
首先我们将 $\lambda_1=-1$代入方程:
$\begin{pmatrix} -1 & 1 & 1 \ 0 & 3 & 0 \ -4 & 1 & 4 \end{pmatrix} \begin{pmatrix} x_1 \ x_2\ x_3 \end{pmatrix}=\begin{pmatrix} 0 \ 0\0 \end{pmatrix}$ 化简得到 $\begin{pmatrix} 1 & 0 & -1 \ 0 & 1 & 0 \ 0 & 0 & 0 \end{pmatrix}$
所以 $\begin{cases}x_1 =x_3\ x_2=0\end{cases}$ => $\xi_1=\begin{pmatrix} 1 \ 0\1 \end{pmatrix}$ 特征向量: $p_1=k\begin{pmatrix}1 \ 0\1 \end{pmatrix}$
对于 $\lambda=2$ 我们带入得到
$\begin{pmatrix} -4 & 1 & 1 \ 0 & 0 & 0 \ -4 & 1 & 1 \end{pmatrix}\begin{pmatrix} x_1 \ x_2\ x_3 \end{pmatrix}=\begin{pmatrix} 0 \ 0\ 0 \end{pmatrix}$ 化简得到: $\begin{pmatrix} -4 & 1 & 1 \ 0 & 0 & 0 \ 0 & 0 & 0 \end{pmatrix}$
所以 $-4x_1+x_2+x_3=0 \rightarrow x_2=4x_1-x_3$
对于这种情况, $x_1和x_3$ 都是随我们取0,我们一般取 0,1和1,0 两种情况
于是 $\xi_2= \begin{pmatrix} 1 \ 4\0 \end{pmatrix}$ ,$\xi_3 = \begin{pmatrix} 0 \ -1 \1 \end{pmatrix}$ A对应于$\lambda=2$ 得全部特征向量就是:$k_1\begin{pmatrix} 1 \ 4\0 \end{pmatrix}+k_2\begin{pmatrix} 0 \ -1 \1 \end{pmatrix}$ $k_1,k_2$不全为0

第三个: $\begin{pmatrix} -1 & 1 & 0 \ -4 & 3 & 0 \ 1 & 0 & 2 \end{pmatrix}$求这个矩阵的特征值和特征向量
$|A-\lambda E|=0\Rightarrow (2-\lambda)\begin{vmatrix} 1-\lambda & 1 \ -4 & 2-\lambda \end{vmatrix}=(2-\lambda)(\lambda-1)^2=0$
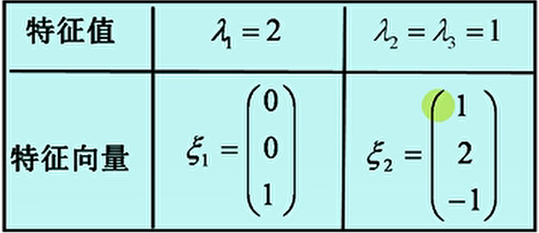
得到特征值 $\lambda_1=2,\lambda_2=\lambda_3=1$
对于 $\lambda_1=2$ 我们可以得到
$\begin{pmatrix} -3 & 1 & 0 \ -4 & 1 & 0 \ 1 & 0 & 0 \end{pmatrix}\begin{pmatrix} x_1 \ x_2\x_3 \end{pmatrix}=\begin{pmatrix}0\ 0\0 \end{pmatrix}$ 化简得 $\begin{pmatrix} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 0 \end{pmatrix}$
于是 $\begin{cases}x{1}=0\ x{2}=0\end{cases}$ , $x_3$随我们取,我们可以取 1。所以 $\xi_1=\begin{pmatrix}0\ 0\0 \end{pmatrix},p_1=k\begin{pmatrix}0\ 0\1 \end{pmatrix}(k\ne 0)$
对于 $\lambda_2=\lambda_3=1$
$\begin{pmatrix} -2 & 1 & 0 \ -4 & 2 & 0 \ 1 & 0 & 1 \end{pmatrix} \begin{pmatrix} x_1 \ x_2\x_3 \end{pmatrix}=\begin{pmatrix}0\ 0\0 \end{pmatrix}$ 化简得到 $\begin{pmatrix} 0 & 1 & 2 \ 0 & 0 & 0 \ 1 & 0 &1 \end{pmatrix}$
所以 $\begin{cases}x{1}=-x{3}\ x{2}=-2x{3}\end{cases}$ $\xi_2=\begin{pmatrix}1\ 2 \ -1 \end{pmatrix}$ $p=k\begin{pmatrix}1\ 2\ -1 \end{pmatrix}$
所以这个2重特征根只确定了一个线性无关的特征向量!
对于上面两个例子我们可以得到一些结论:
特征方程的一个 s重根最多能确定 s 个线性无关的特征向量。即一个特征值的特征空间维数(集合重数) 不会大于该特征值的代数重数 s
因此,每一个特征单根只能确定一个线性无关的特征向量。
- 一个二重特征根最多能确定两个线性无关的特征向量
- 所以,一个n阶矩阵A最多有 n个线性无关的特征向量
拓展: 矩阵A的s重特征根能否确定s个线性无关的特征向量,直接影响到矩阵 A 能否对角化。一个n阶矩阵A能对角化的条件就是它有n个线性无关的特征向量。因此,只有A的每一个s重根都能确定s个线性无关的特征向量(几何重数=代数重数) 矩阵A才能对角化
关于对角化,我会在下一篇博客中讲到。
特征值和特征向量的性质
特征值和矩阵之间巧妙的关系
矩阵的行列式等于它全体特征值之积 $\lambda_1\lambda_2\cdots\lambda_n=|A|$
矩阵的特征值之和等于矩阵的迹 $a{11}+a{22}+\cdots+a_{nn}=\lambda_1+\lambda_2+\cdots+\lambda_n=trA$
性质 1
1)设p是矩阵A的属于特征值$\lambda$ 的特征向量,则 $kp(k\ne 0)$ 也是A的属于 $\lambda$ 的特征向量
2)设 $p_1,\cdots,p_s$ 是方阵A的属于特征值 $\lambda$ 的特征向量,则 $p= k_1p_1+\cdots+k_sp_s \ne 0 $也是A的属于$\lambda$ 的特征向量
也就是说,属于同一特征值的若干个特征向量的非零线性组合仍然是属于该特征值的特征向量
性质 2
设 $\lambda$ 是方阵 A的特征值,则$\lambda^2$ 也是$A^2$ 的特征值
证明: $Ap=\lambda p$ , 则 $A^2p =A(Ap)=A(\lambda p)=\lambda Ap=\lambda(\lambda p)=\lambda^2 p$ 所以 $\lambda^2$ 也是 $A^2$ 的特征值
以上证明可以看出:若p是A的属于特征值 $\lambda$ 的特征向量,则p也是 $A^2$ 的属于特征值 $\lambda^2$ 的特征向量
进而,我们可以推断,A的特征值的多项式 是 A 的同一个多项式的特征值 $Ap=\lambda p \Rightarrow \varphi(A)p =\varphi(\lambda)p$
A的特征向量也是A的多项式的特征向量
性质3
设$\lambda$ 是可逆矩阵A的特征值,则 $\lambda\ne 0$ ,且 $1/\lambda $ 是矩阵 $A^{-1}$ 的特征值
证明 设非零向量p是A的属于$\lambda$ 的特征向量:$Ap=\lambda p$
$p=A^{-1}\lambda p =\lambda A^{-1}p$ 因为 p不是零向量,所以 $\lambda\ne 0$
$A^{-1}p=\frac{1}{\lambda}p$ 所以$\lambda^{-1}$ 是矩阵$A^{-1}$ 的特征值
性质4
一个矩阵A与其转置矩阵$A^T$ 有相同的特征多项式,从而有相同的特征值
$|A^T-\lambda E|=|(A-\lambda E)^T|=|A-\lambda E|$
但是注意了 ,对于同一个特征值 $\lambda$ ,$A$ 与 $A^T$ 并不一定有相同的特征向量!
综上,我们可以列出一张简单的表格
A* — 伴随矩阵的定义:某矩阵A各元素的代数余子式,组成一个新的矩阵后再进行一下转置,叫做A的伴随矩阵。
| 矩阵 | 特征值 | 特征向量 | ||||
|---|---|---|---|---|---|---|
| A | $\lambda$ | p | ||||
| $A^k$ | $\lambda^k$ | p | ||||
| $\varphi(A)$(多项式) | $\varphi(\lambda)$ (多项式) | p | ||||
| $A^{-1}$ | $\lambda^{-1}$ | p | ||||
| $A^*= | A | A^{-1}$ | $ | A | \lambda^{-1}$ | p |
| $A^T$ | $\lambda$ | 不一定是p |
下面我用三个例子来运用说明这些性质:
第一个: 设3阶可逆矩阵A的特征值
$\lambda_1=1,\lambda_2=-2,\lambda_3=3$ ,求矩阵 $A^3+2(A^{-1})^2+3A^*-2E$ 的特征值
解: 设非零向量p是A的属于特征值 $\lambda$ 的特征向量
则 $Ap=\lambda p$ $A^3p= \lambda^3p$
$(A^{-1})^2p =(\lambda^{-2})p $
原式等于: $\lambda^3p+2(\lambda^{-1})p+3|A|\lambda^{-1} p-2p$
令 $\varphi(\lambda)=\lambda^3+\frac{2}{\lambda^2}-\frac{6}{\lambda}-2$ , $\varphi(A)p=\varphi(\lambda)p$
然后分别将三个$\lambda$ 的值带入即可
第二个:

第三个:
已知 3阶矩阵A有特征值 1,2,3 ,求 $|A^3-5A^2+7A|$
解: 令 $\varphi(x)=x^3-5x^2+7x$
则 $A^3-5A^2+7A=\varphi(A)$ 有特征值 $\varphi(1)=3,\varphi(2)=2,\varphi(3)=3$
由矩阵行列式的值等于其特征值之积可以得到: $|A^3-5A^2+7A|=|\varphi(A)|=323=18$
相似矩阵
定义
设A和B是n阶矩阵,如果有n阶可逆矩阵P,使得 $P^{-1}AP=B$ h或者 $AP=PB$
则称 A与B 相似 ,记作 $A\sim B$ , 我们也说 B是A的相似矩阵
$A\rightarrow P^{-1}AP=B$ 称为相似变换,P就是变换矩阵
矩阵的相似关系具有一下性质:
- 自反性(reflexivity) :$A\sim A$
- 对称性 (symmetry) :$A\sim B \Rightarrow B\sim A$
- 传递性 (transitivity): $A\sim B,B\sim C\Rightarrow A\sim C$
性质
- 相似矩阵拥有相同的特征多项式,从而有相同的特征值、相同的行列式(全体特征值之积)和相同的迹(全体特征值之和),相同的秩
- 相似矩阵一定是等价矩阵
- 相似变换不能保持矩阵的对称性
- 相似矩阵不一定有相同的特征向量
- 相似矩阵的幂,多项式,逆矩阵,转置矩阵 ,伴随矩阵 都是相似的
可以这样来列2张表格

