算法设计与分析整理
Lec1
排序算法
算法复杂度分析
我们要搞清楚几个概念:
$O:f(n)=O(g(n))$,也就就是 $\exists c>0$和$n_0$
当 $n\geq n_0$ 的时候 ,有$f(n)\leq cg(n)$ 。也就是说,$g(n)$ 是 $f(n)$ 的渐进上界
e.g. $2n^2=O(n^3)(c=1,n_0=2)$ ,也可以说 $2n^2\in O(n^3)$
$\Omega:f(n)=\Omega(g(n))$,也就是 $\exists c>0,n_0$
当 $n\geq n_0$ 的时候 ,有$f(n)\geq cg(n)$ 。 也就是说 $g(n)$ 是 $f(n)$的渐近下界
e.g.$n^{0.5}=\Omega(\lg n)$
$\Theta:f(n)=\Theta(g(n))$, 也就是 $\exists c_1>0,\exists c_2>0,n_0$
当 $n\geq n_0$ 的时候 ,有 $c_1g(n)\leq f(n)\leq c_2g(n)$ 。也就是说 g(n) 与 f(n) 同阶
当一个n足够大的时候, 一个 $\Theta(n^2)$ 的算法始终会击败一个 $\Theta(n^3)$ 的算法
e.g. $\frac{1}{2}n^2+2n=\Theta(n^2)$
插入排序算法分析
Worst case: Input reverse sorted
$T(n)=\sum_{j=2}^n\Theta(j)=\Theta(n^2)$
Average case: All permutations equally likely
$T(n)=\sum_{j=2}^n\Theta(j/2)=\Theta(n^2)$
合并排序算法分析
合并算法 $A[1\cdots n]$
- If n=1, done
- Recursively sort $A[1,\cdots,[n/2]]$ and $A[[n/2]+1,\cdots ,n]$
- Merge the 2 sorted lists
$T\left( n\right) =\begin{cases}\Theta \left( 1\right)ifn=1\ 2T\left( \frac{n}{2}\right) +\Theta (n)ifn >1\end{cases}$
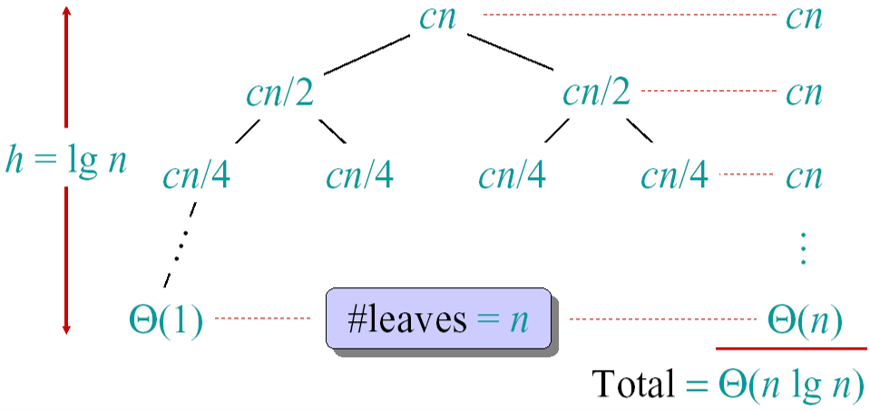
Three methods: Substitution(代入法), Iteration(递归树法), Master(主方法)
主定理
$T(n) = aT(n/b) + f(n)$
我们要比较 $f(n)$ and $n^{log_ba}$
如果 $f(n)$ 增长得比 $n^{log_ba}$ 慢,那么就是 $\Theta(n^{log_ba})$
$f(n)$ 是和 $n^{log_ba}$ 同阶的,那么结果是 $\Theta(n^{log_ba}\log n)$
$f(n)$ 增长得比 $n^{log_ba}$ 更快,那么就是 $\Theta(f(n))$

对于a: $T(n)=4T(n/3)+n\lg n$

对于b: $3T(n/3)+n/\lg n$

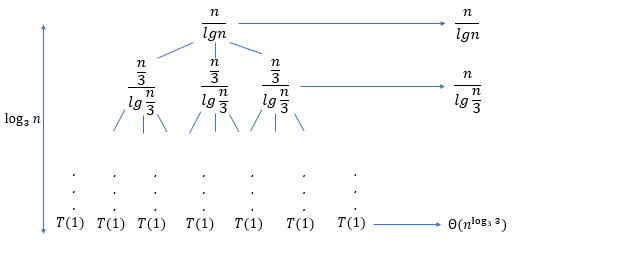
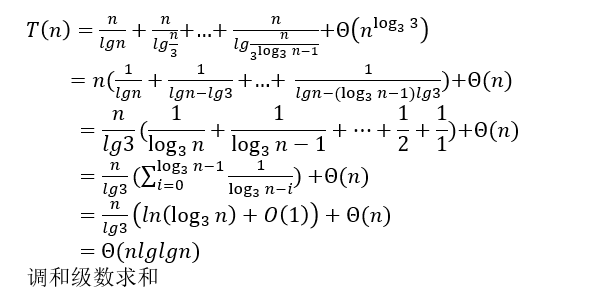
对于c: $T(n)=4T(n/2)+n^2\sqrt{n}$
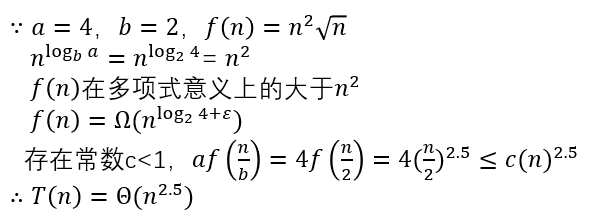
对于d

对于e: $T(n)=2T(n/2)+n/\lg n$
和 b 一样
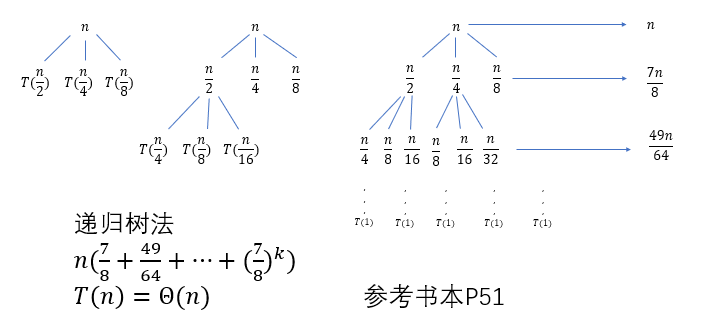
对于f:$T(n)=T(n/2)+T(n/4)+T(n/8)+n$
对于g:$T(n)=T(n-1)+\frac{1}{n}$
调和级数求和: $T(n)=\Theta(\lg n)$
对于h: $T(n)=T(n-1)+\lg n$
$\lg n+\lg (n-1)+\lg(n-2)+\cdots+\lg2+\lg1 = \lg(n!)$
$T(n)=\Theta(n\lg n)$
对于i:$T(n)=T(n-2)+\frac{1}{\lg n}$
$\frac{1}{\lg n}+\frac{1}{\lg(n-1)}+\frac{1}{\lg(n-2)}+\frac{1}{\lg(n-3)}+\cdots+\frac{1}{lg3}+\frac{1}{\lg2}$
$T(n)=\Theta(\frac{n}{\lg n})$
对于j: $T(n)=\sqrt{n}T(\sqrt{n})+n$
