人工神经网络

Posted on
Words count in article: 5.2k | Reading time ≈ 18

人工神经网络

感性认识

神经元

首先我们来讲讲 Neuron 神经元。他是组成神经网络的基本结构。

我们都知道生物上的神经元，即神经细胞是长什么样的。深度学习的目标就是模拟大脑的运行，但是我们怎么用机器来模拟神经元呢?

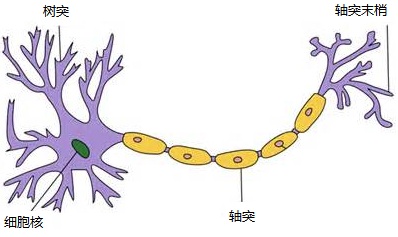
这是一个神经元的模型，树突和轴突就是用来传递神经信号的。(高中生物？？？？)

我们可以用一个简图来模拟上述操作：

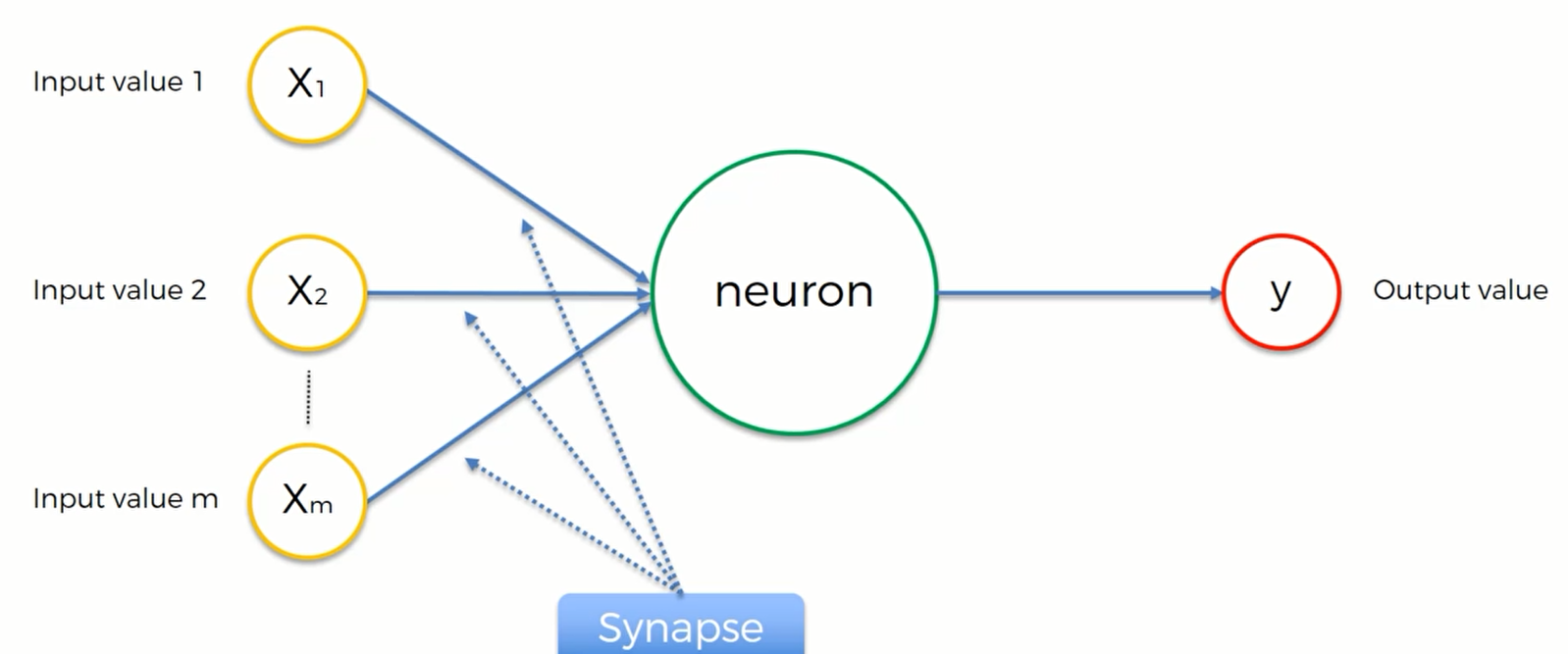
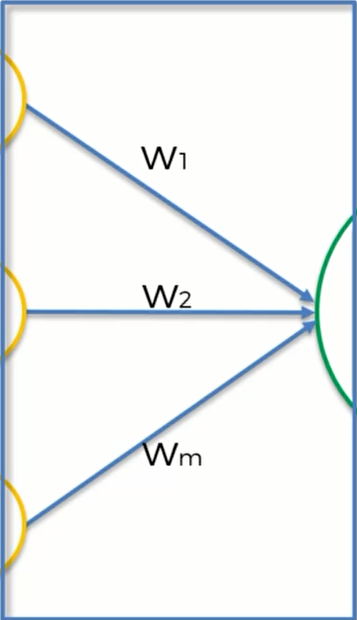
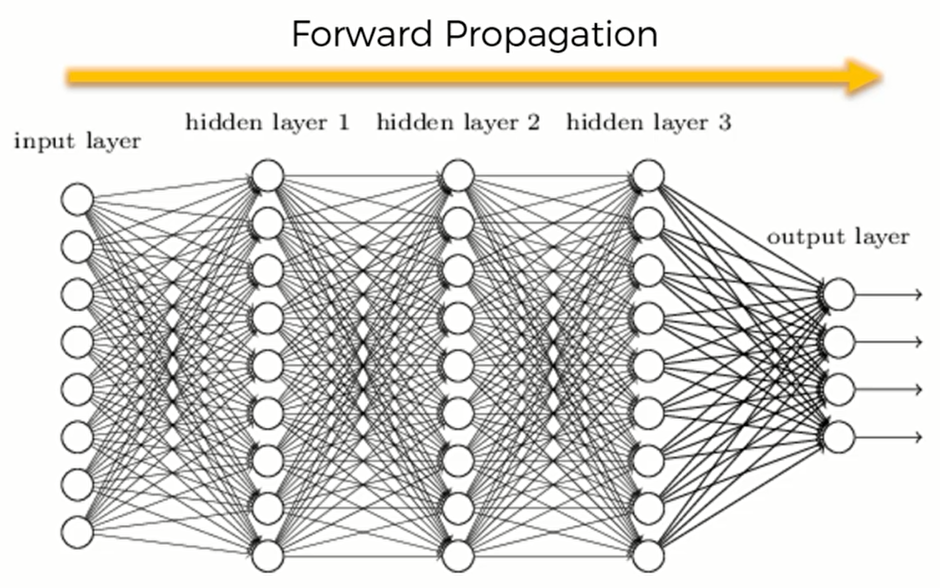
第一层黄色的神经元是信号输入层 。在人类的大脑中，输入层就是我们的各种感觉：视觉、听觉、触觉等，而大脑中的神经元则是用来处理这些器官采集到的电信号的。对于机器，输入一些数据(自变量)，通过神经元产生一个输出值

第二层绿色就是神经元，扮演着我们大脑的角色。我们也叫其隐藏层

第三层是红色的输出值。神经元处理好输入数据后传出一个输出值，并更进一步地传递给下一层

在输入层的内部结构是这样的：

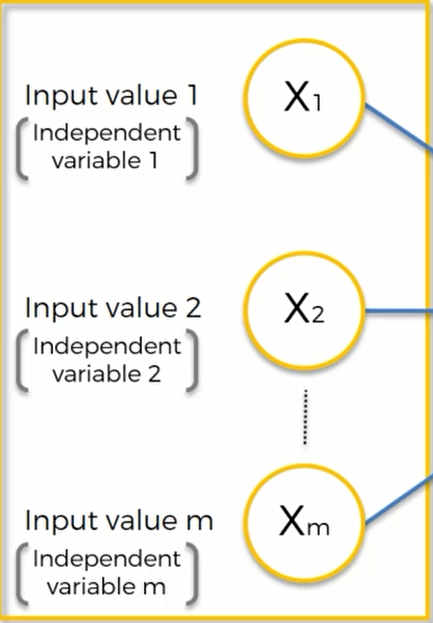
这些自变量都是指每一次观测得到的值，我们可以将其想象成是数据表里的一行数据。我们将用这些数据来训练我们的神经网络模型。但是需要注意的是，在应用他们之前，我们需要将它们标准化(stand)——即让他们平均值为0，方差为1 / 归一化(normalize)—-即让数据分布在0-1之间的值。

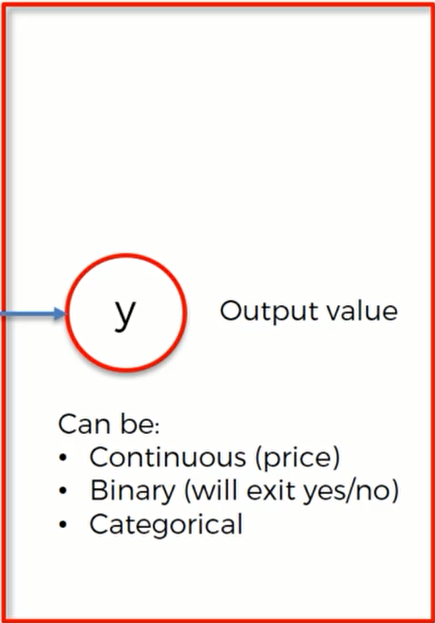
输出值可以是以下几种类型：可以是连续的值，也可以是二进制数，还可以是一个分类变量(如果是分类变量，那么就代表有多个输出值)

接下来我们要讲的是突触(synapses) ，每一个突触都被赋予了一个权重。权重对神经网络非常重要，神经网络就是通过这些权重来学习的。通过计算和改变权重，神经网络决定在每一次计算中对于某个神经元的哪一个信号比较重要、哪个比较不重要，以及哪个信号可以传递下去、那个信号应该被屏蔽等等

所以权重非常关键，当我们在训练神经网络的时候基本上就是在调节权重，这也是为什么我们要学梯度下降和反向传播算法的原因了

最后我们来讲讲神经元，神经元里到底发生了什么？

第一步，神经元会将 输入值* 权重 求和

$\sum_{i=1}^{m}w_ix_i$

第二步，运用激活函数 $\phi(\sum_{i=1}^m w_ix_i)$ ,这样神经元就可以知道它是否需要让一个信号通过

第三步，如果神经元决定通过这个信号，那么它就会将其输出给下一个神经元

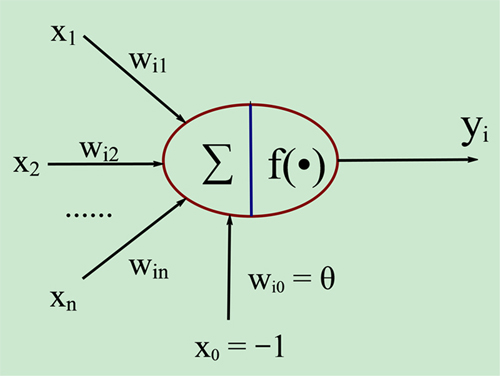
神经元综合的输入信号和偏置（符号为 -1~1）相加之后产生当前神经元最终的处理信号net，该信号称为净激活或净激励（net activation），激活信号作为上图中圆圈的右半部分f（）函数的输入，即f(net)； f称为激活函数或激励函数（Activation Function），*激活函数的主要作用是加入非线性因素，解决线性模型的表达、分类能力不足的问题。上图中y是当前神经元的输出。

激活函数

激活函数有很多很多种，我们这里讲四种比较常用的激活函数

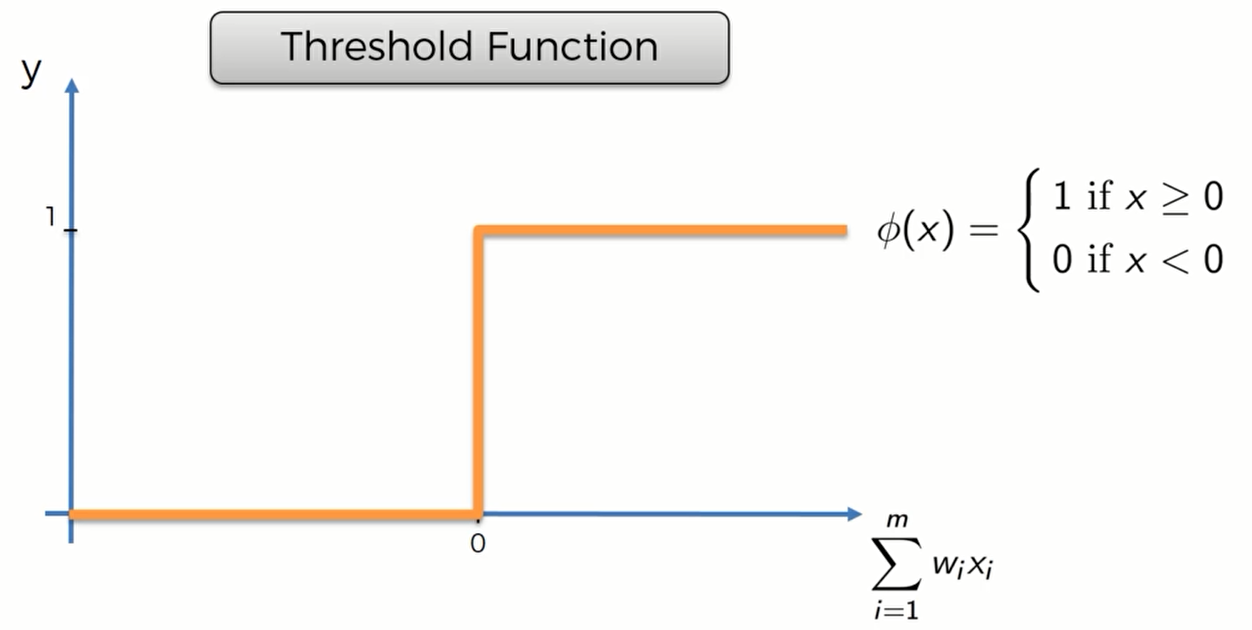
Threshold Function 阈值函数

阈值函数很简单，y轴只有0或者1。如果输入阈值函数的值权重和小于0的话，阈值函数输出0；如果大于0，则输出1.

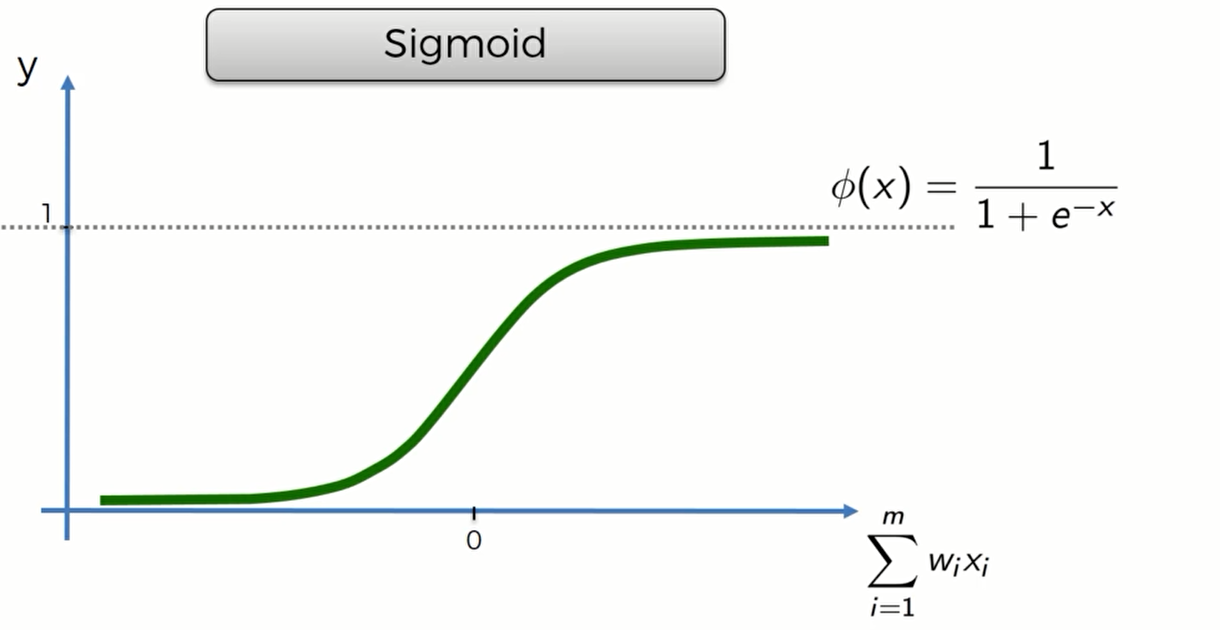
Sigmoid Function

这个函数的优点是一条光滑的曲线，当输入值小于0的时候，y接近0；当输入值大于0的时候，y接近1

Rectifier function(ReLU)

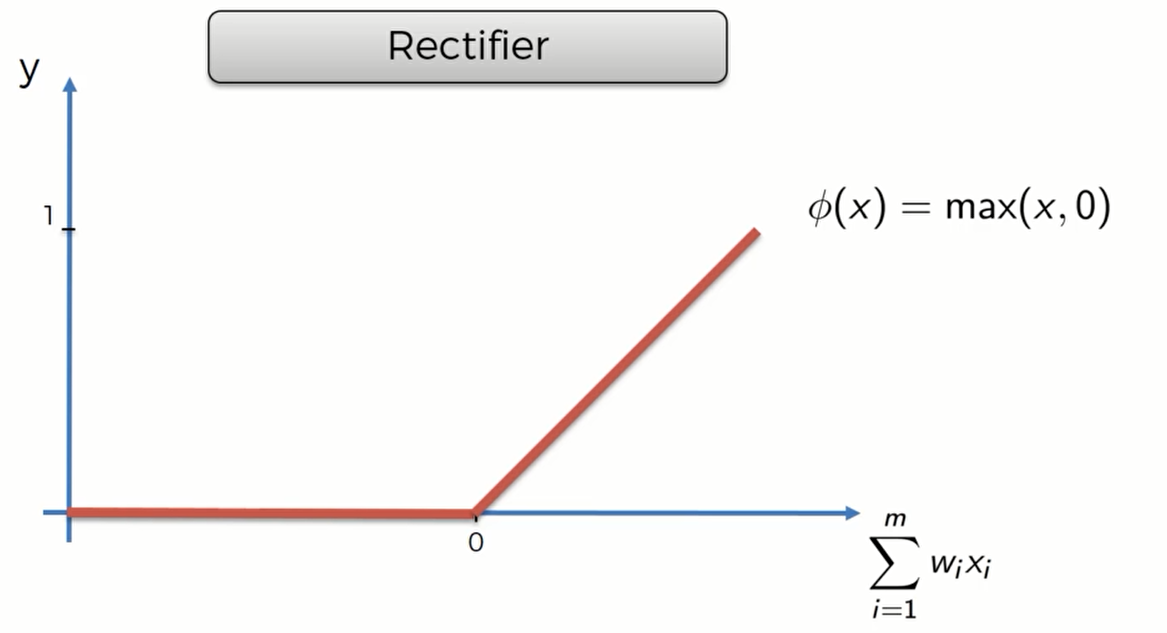
Rectifier function 是近来比较流行的激活函数，当输入信号小于0时，输出为0；当输入信号大于0时，输出等于输入。

ReLU的优点：

  1. ReLU是部分线性的，并且不会出现过饱和的现象，使用ReLU得到的随机梯度下降法（SGD）的收敛速度比Sigmodi和tanh都快。

  2. ReLU只需要一个阈值就可以得到激活值，不需要像Sigmoid一样需要复杂的指数运算。

ReLU的缺点：

在训练的过程中，ReLU神经元比价脆弱容易失去作用。例如当ReLU神经元接收到一个非常大的的梯度数据流之后，这个神经元有可能再也不会对任何输入的数据有反映了，所以在训练的时候要设置一个较小的合适的学习率参数。

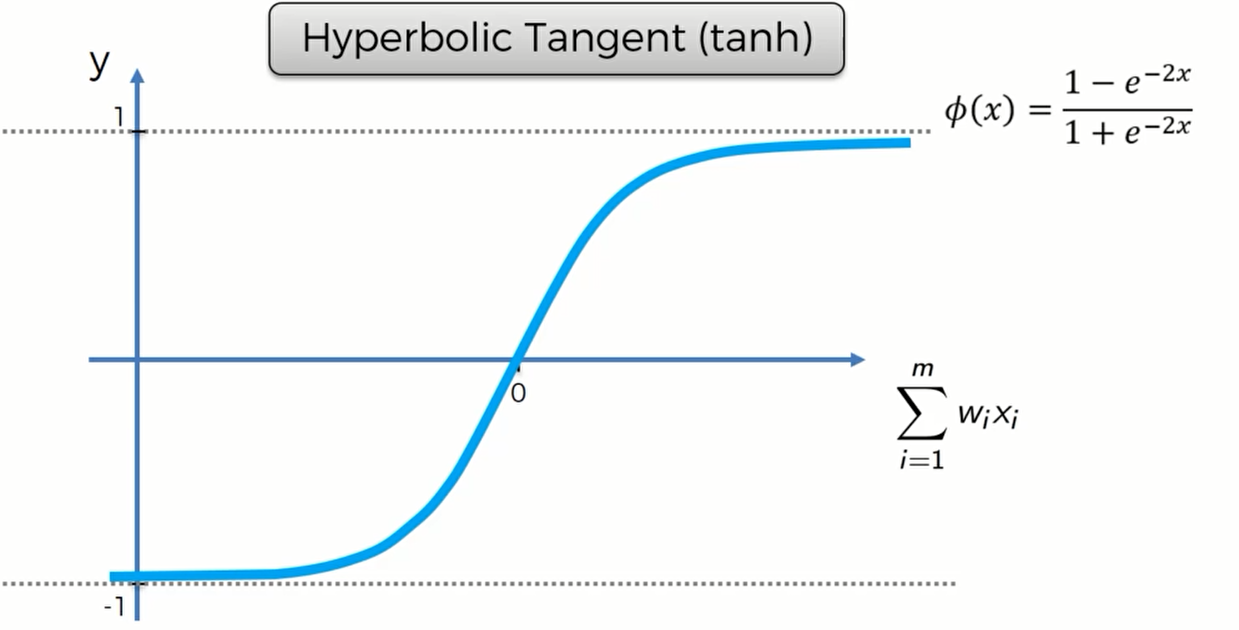
tanh

tanh是Sigmoid函数的变形，tanh的均值是0，在实际应用中有比Sigmoid更好的效果。

拓展资料： http://jmlr.org/proceedings/papers/v15/glorot11a/glorot11a.pdf

现在我们来做两个练习：

假设我们的输出值只为0或者1，那么我们应该怎么选择激活函数？

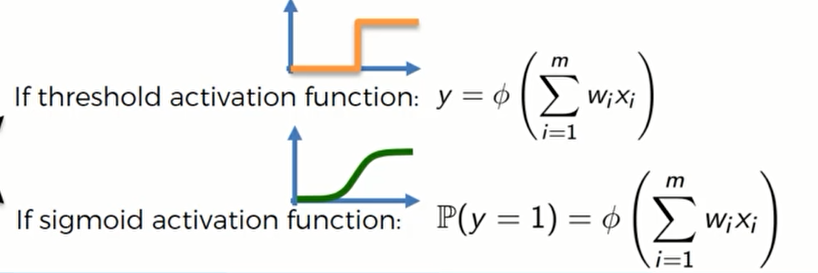
我们可以选择两种，第一种就是Threshold 激活函数，因为y轴只能是0或者1；第二种则是sigmoid函数,用它来表示取到0或者1的概率。

第二个练习是一个应用，假设我们的神经网络长这样:

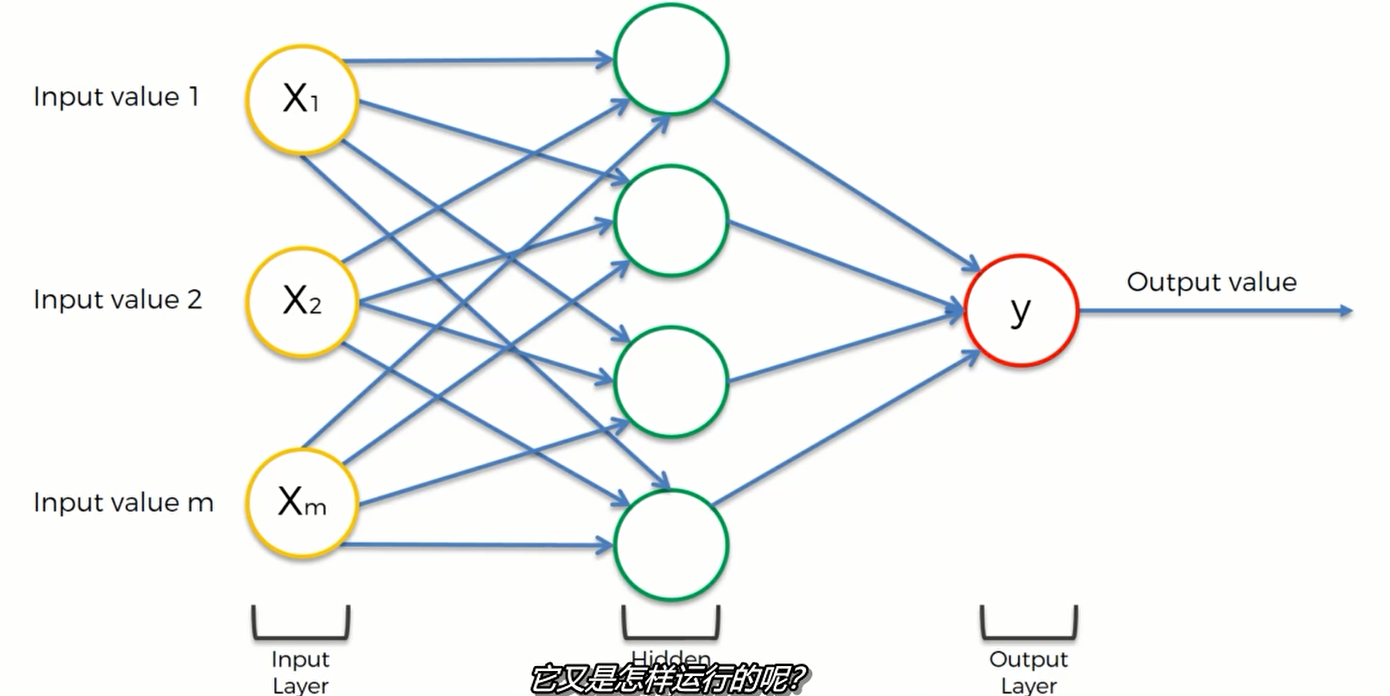
一般，我们先用整流函数(ReLU) 再使用 sigmoid函数

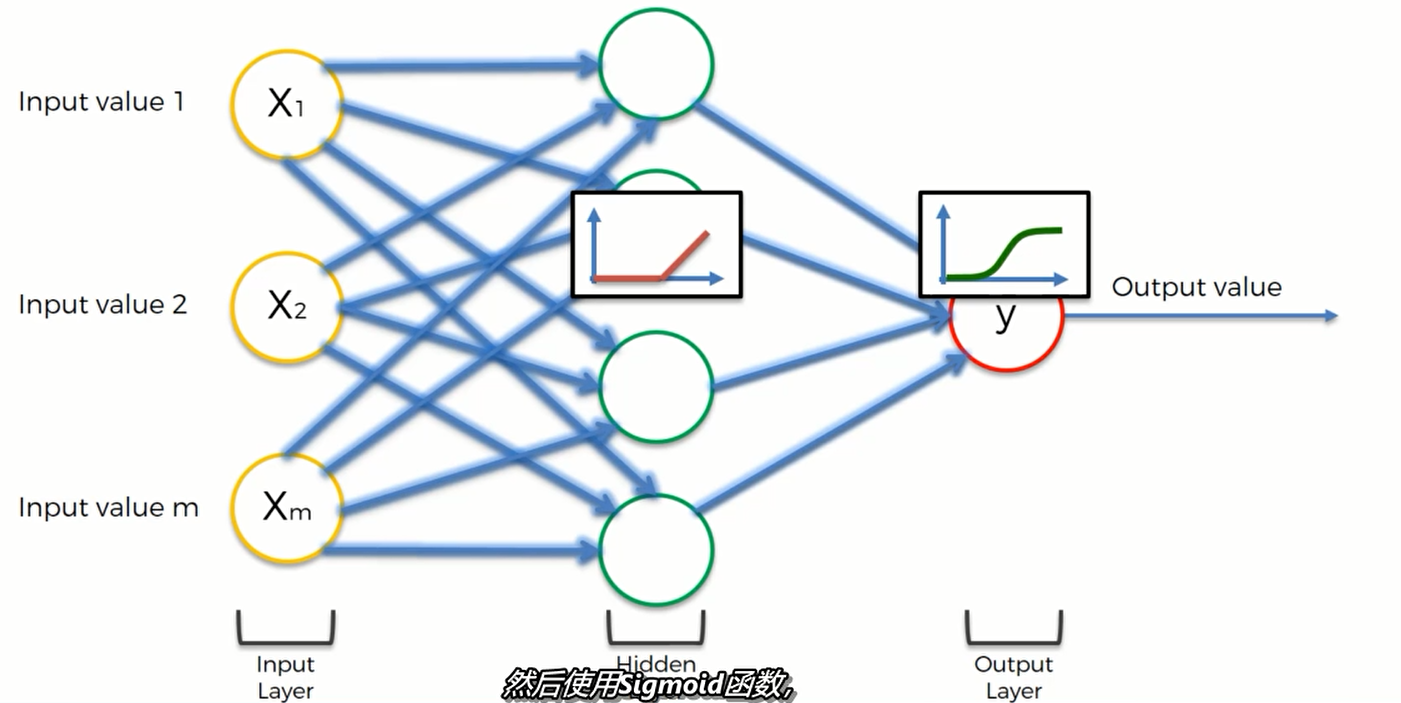
即在隐藏层使用ReLU，在输出层使用Sigmoid函数

神经网络如何工作

现在我们来看一个实例，看看可以如何应用神经网络来解决一些实际的问题

我们将用房地产评估的例子来作为介绍。看看怎么把房地产的参数引入神经网络并预测房地产的价值

我们暂时不讲怎么训练这个神经网络，假设它已经被训练好了，仅仅来看看神经网络是怎么来预测的。

我们假设，一个房地产的价格和四个参数有关：

  • Area面积
  • Bedrooms 卧室数目
  • Distance to city 离市中心多远
  • Age 房龄

这四个变量将是我们的输入值，输出值是房子的预估价值。

如果没有隐藏层，那么整个模型长这样：可以简单地给它们一个权重，然后price直接等于权重和

这个模型也是大多数机器学习中回归算法的模型

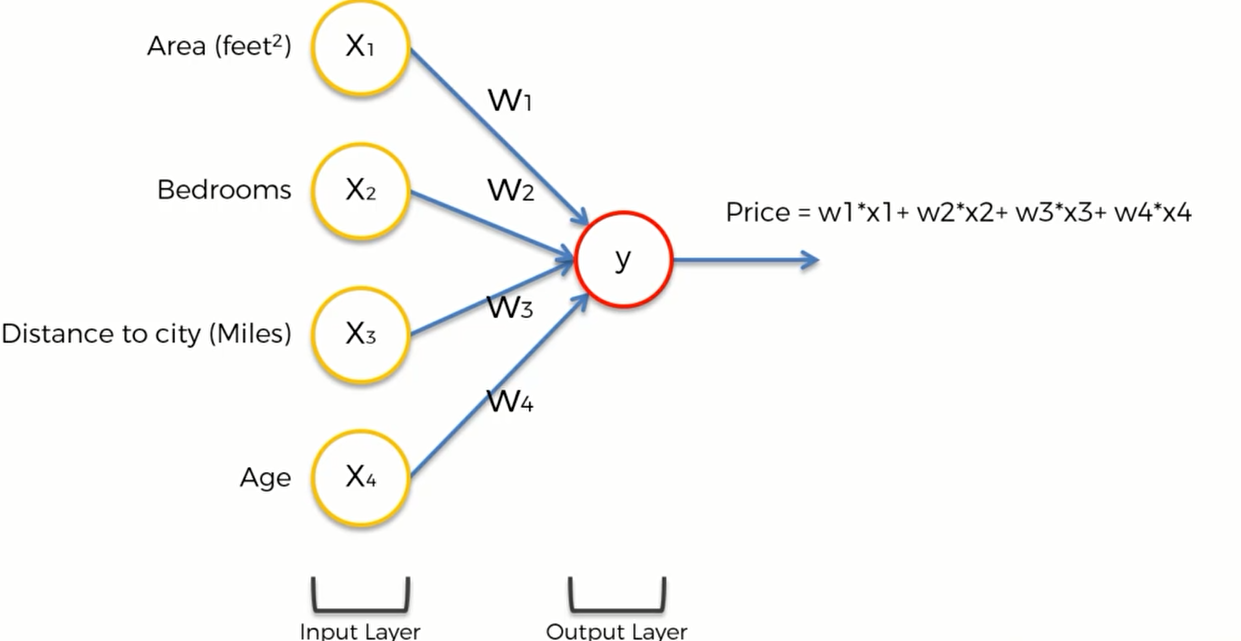
这就是神经网络的强大之处，即使没有隐藏层，也可以进行一些预测。隐藏层让整个模型变得更加灵活和强大。能提高预测的准确率。

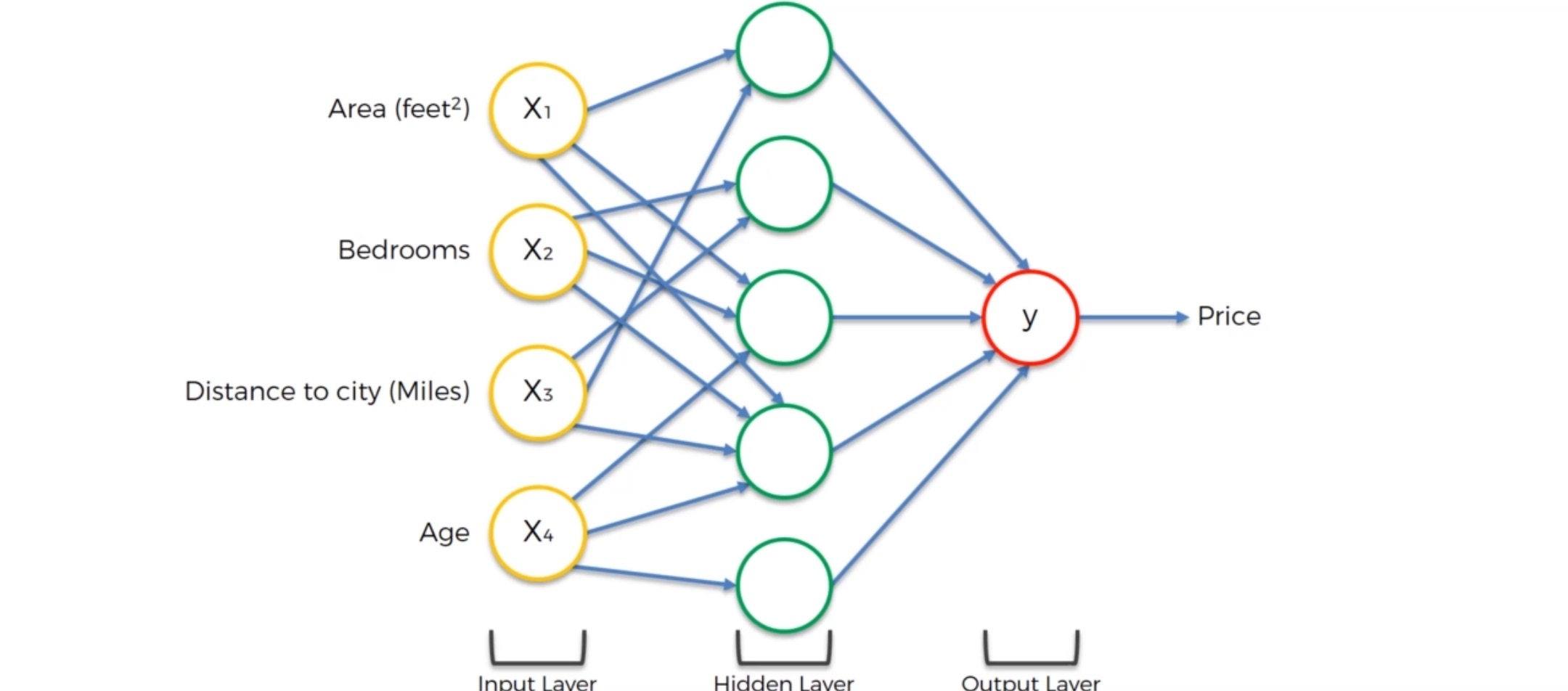
现在我们加入隐藏层：

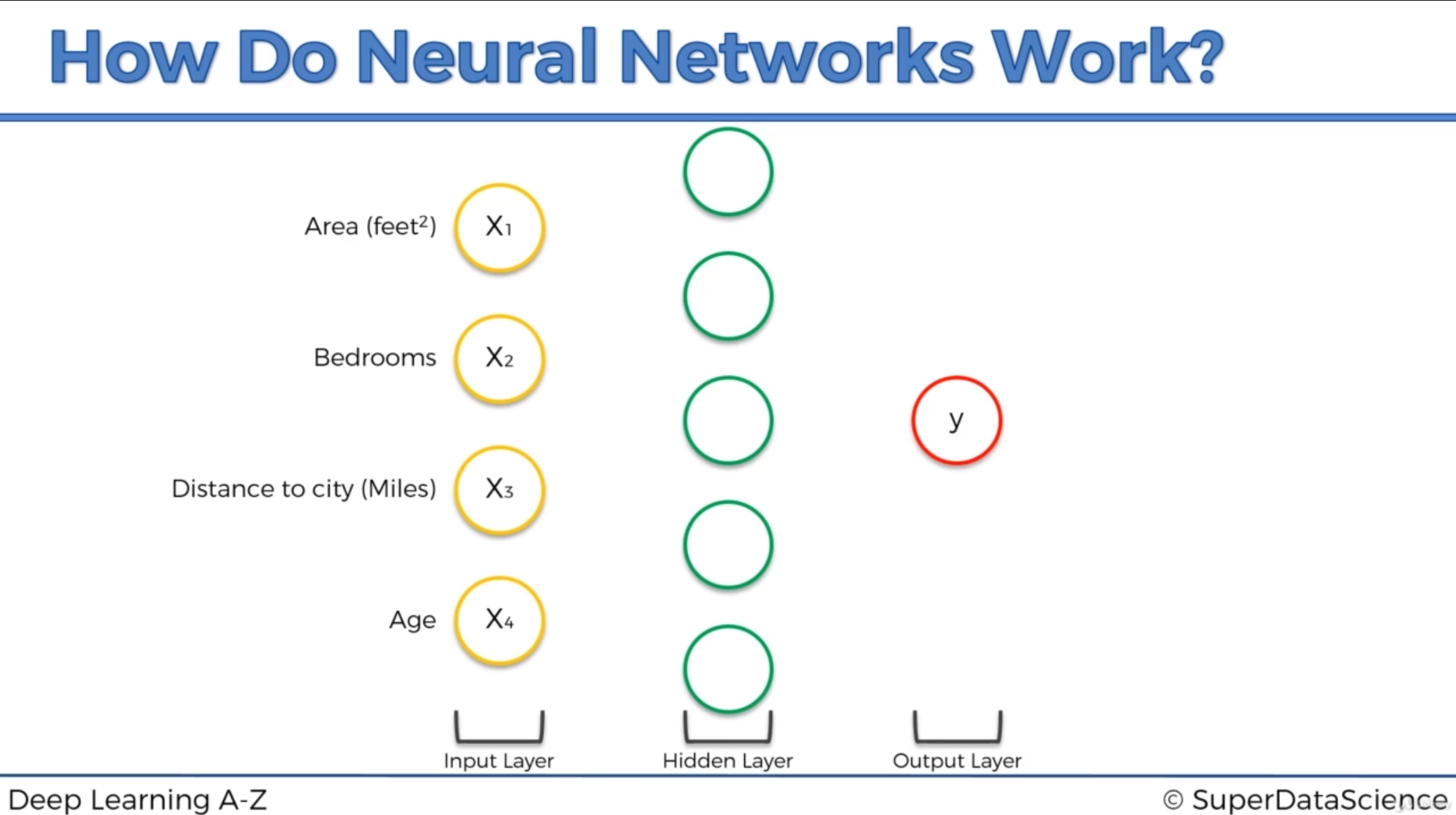
现在假设四个参数都和隐藏层的第一个神经元有突触，这些突触上有不同的权重。

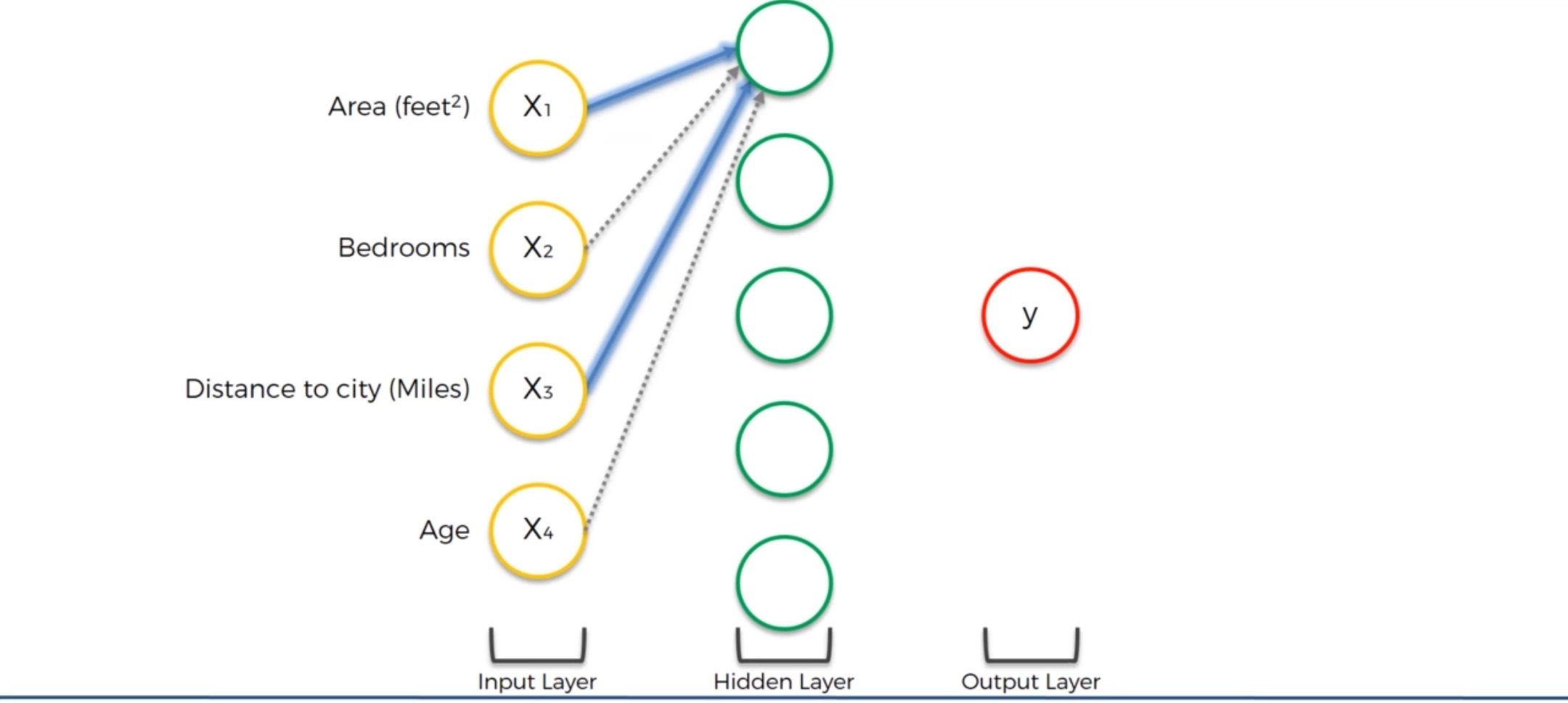
我们看到对于第一个神经元，它只关注 Area和Distance to City，也就是说它认为这两个参数对房价的影响比较大。这个神经元的职能就是来寻找离城市不远同时面积又大的房产。当这两个参数达到一定水平的时候，激活函数就会激活这个神经元并输出信号并最终影响到输出层的价格。因此，这个神经元并不在乎卧室的数目和房产的年龄。这也是为什么神经网络如此强大的原因：我们拥有很多这样的神经元，每个神经元各司其职——我们也将会看看其他的神经元如何操作

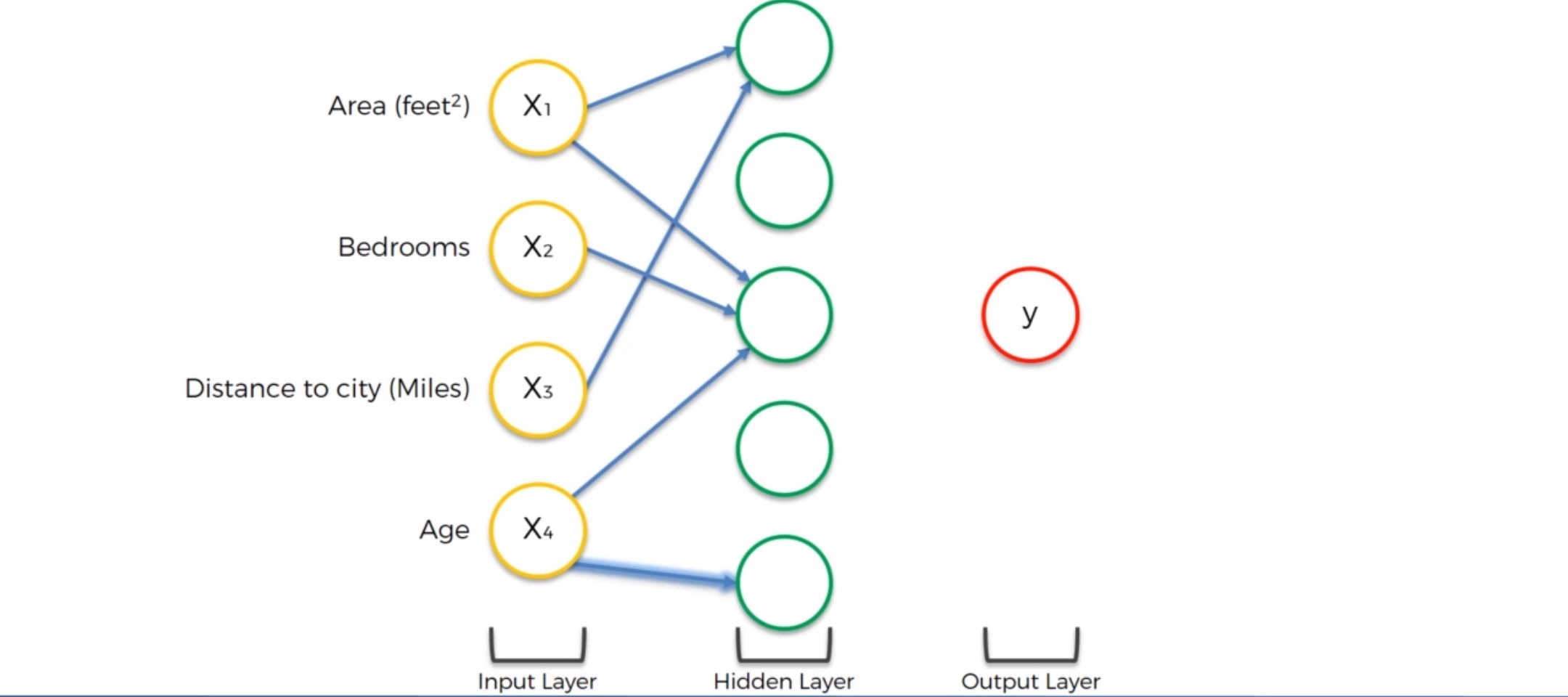
我们来看下一个位于中间位置的神经元：中间这个神经元的输入为三个数据：住房面积，房间个数和房龄。这可能是因为在对数据集进行训练时，神经网络发现这三个数据之间有特定的联系：比如在某一个地区一个家庭拥有很多孩子，常常在找房龄较小、卧室比较多、住房面积又比较大的。所以这个神经元可能就认为一个住房面积比较大的，卧室数目大于3个的，房子又比较新的房型在这个房地产市场非常吃香，于是满足条件的就会通过激活函数把神经元激活。

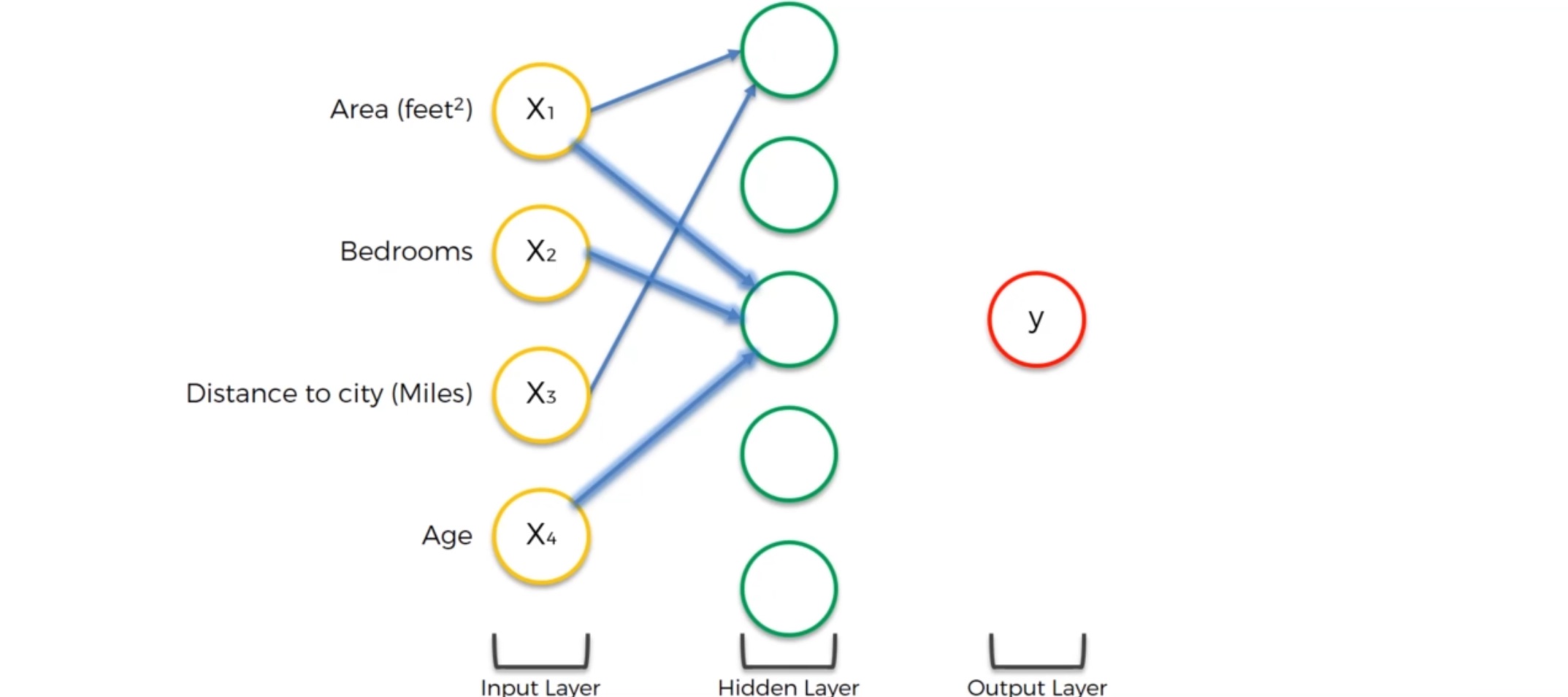
还有可能是这样一个情况：一个神经元仅仅接收来自一个输入层的数据：Age
这可能是因为这个神经元认为房龄的长短对房价的影响比较重要 。比如说有些老房子比较破，房价会低；新房子房价会高。但是有些房子(如上海花园洋房) 是历史遗留财产，价格可能又会更高一些。

这就是神经元的例子，他会发现我们用肉眼很难发现的规律。 隐藏层提高了整个神经网络模型的灵活性，能找到那些特别的特征并将它们结合起来考虑。每一个神经元都不能完整预测出房价，但把它们放在一起，可能就会得到意想不到的结果。

神经网络如何学习

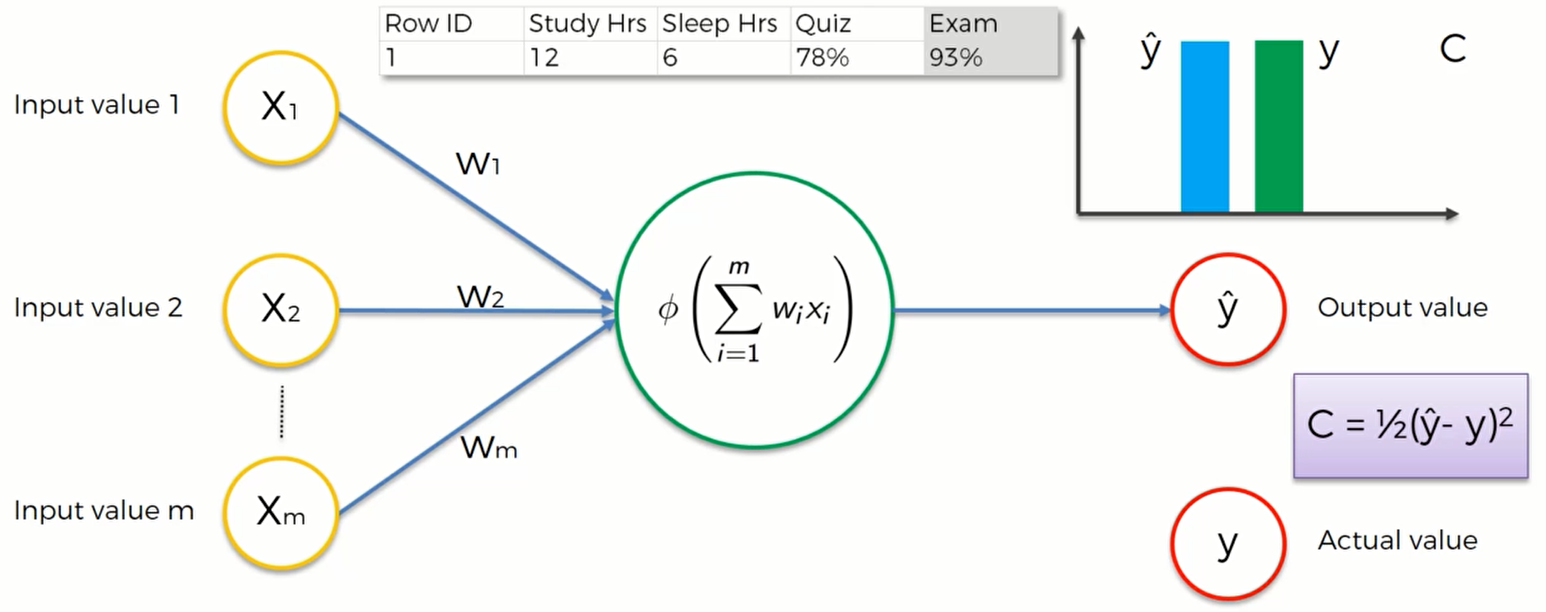
这里有一个基本的神经网络模型，隐藏层只有一个神经元。它被称为：“单层前馈神经网络”，也叫感知机“perception”。这个模型的输出值是 $\hat y$ ，但这并不是真实值，真实值是y，两者之间存在一个较大的误差。这个误差我们用一个 cost function(损失函数) 来衡量。损失函数有很多种，最常用的就是 $C= \frac{1}{2}(\hat y - y)^2$ .在图像上用柱形图表示如下:

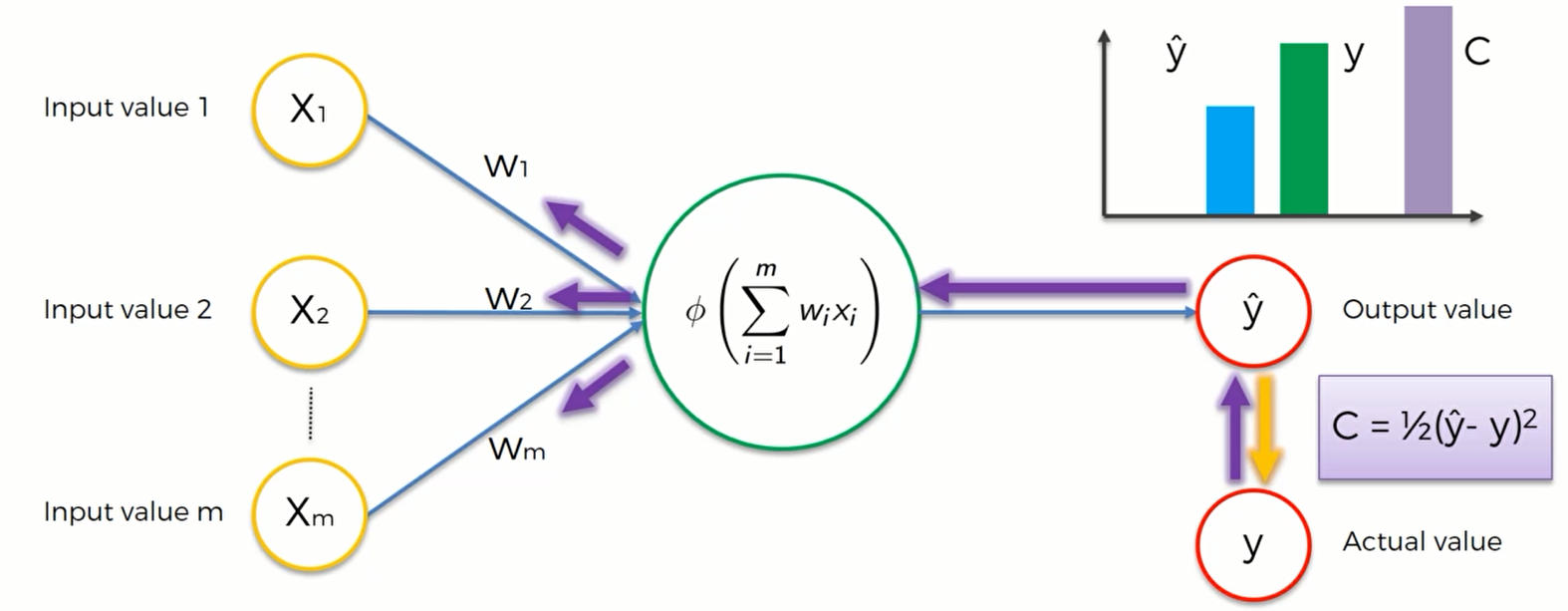
我们的目标就是让损失函数的值尽可能地小，因为其值越小， $\hat y$ 与 $y$ 就越接近，神经网络的学习效果也就越好。所以机器在比较了y与 $\hat y$ 之后，将其差值反馈给神经网络(紫色箭头)，然后神经网络会通过这个信息来更新权重以减少两者之间的差值。所以在神经网络中我们唯一能控制 的就是各个突触的权重

我们多次输入同一行数据，让权重不断调节，努力减小损失函数的值。

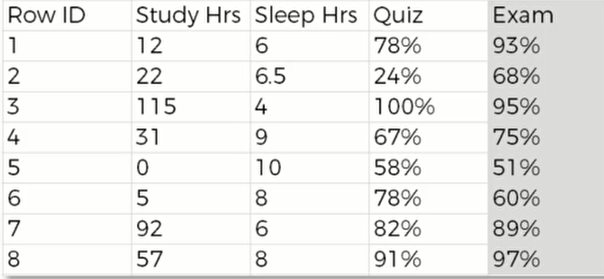
但事实上，一个数据集不可能只有一行数据，完整的数据集如下：

我们要把这些数据都输入到神经网络当中，并得到 $\hat y$ 。随后，我们再将真实的数据用绿色柱体渲染上去。如下图：

(这里实际上只有一个神经元，只是重复了8次)

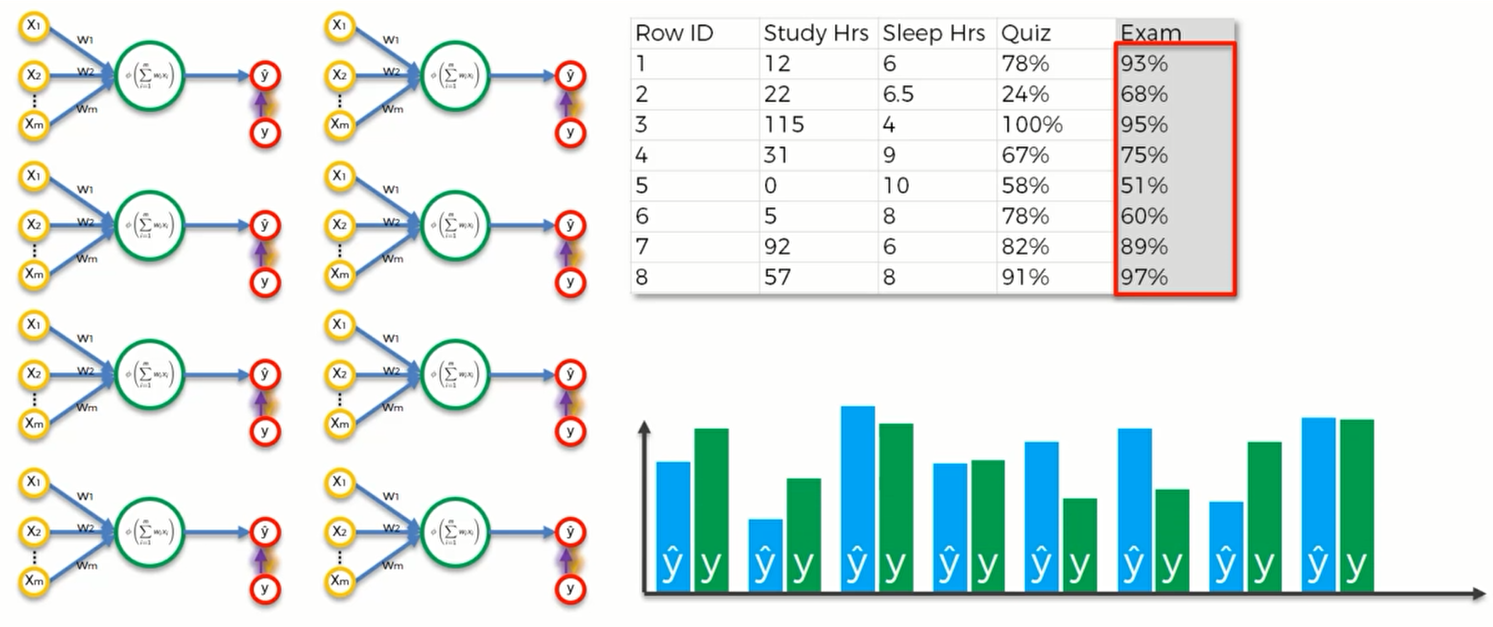
然后我们计算损失函数 $C = \sum \frac{1}{2}(\hat y-y)^2$ 的值，并将其反馈给神经元来让其更新权重。

我们的目标是最小化损失函数，一旦我们找到了损失函数的最小值，就说明整个模型已经训练完毕

拓展资料：

https://stats.stackexchange.com/questions/154879/a-list-of-cost-functions-used-in-neural-networks-alongside-applications

梯度下降和随机梯度下降

我们现在来看，这些权重是怎么被调整的。

要降低代价函数的值，最笨的方法就是取很多不同的权重，然后比较哪些权重组合比较好。 但是随着神经元的增加、突触会变得很多，我们就会被迫遇到 维数困难(Curse of Dimensionality) .比如说我们有25个权重，对每个权重我们可以取1000个不同的值，那么$1000^{25}$ 就等于 $10^{75}$ 次计算，这是一个天文数字

所以我们需要用到梯度下降算法，简单的来说我们就要对损失函数求导并判断其在递增还是递减，一直找到损失函数最低点处。

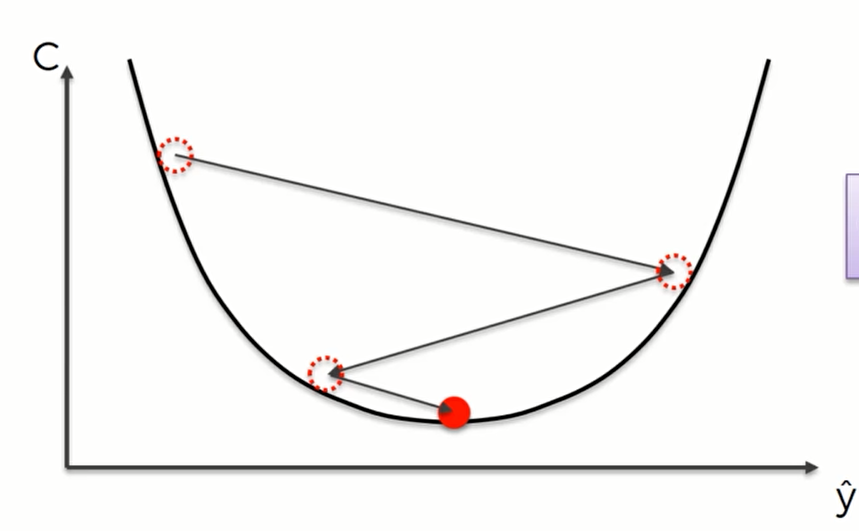
对于一个2维空间，我们可以这样来画

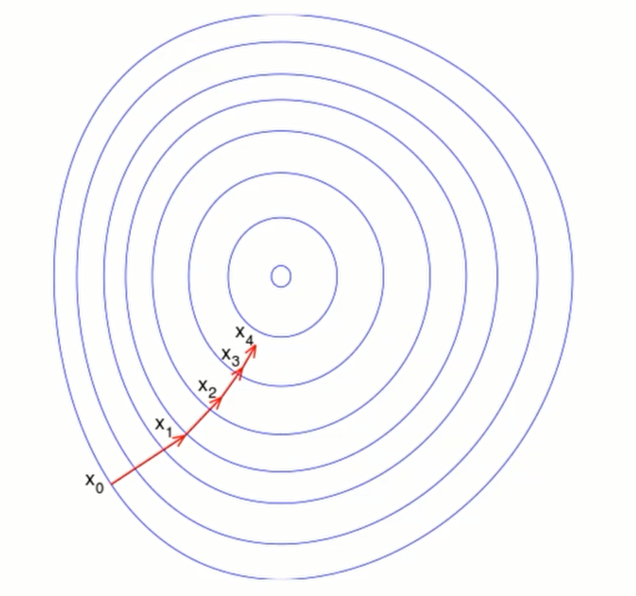
同样，对于3维空间，如下所示：

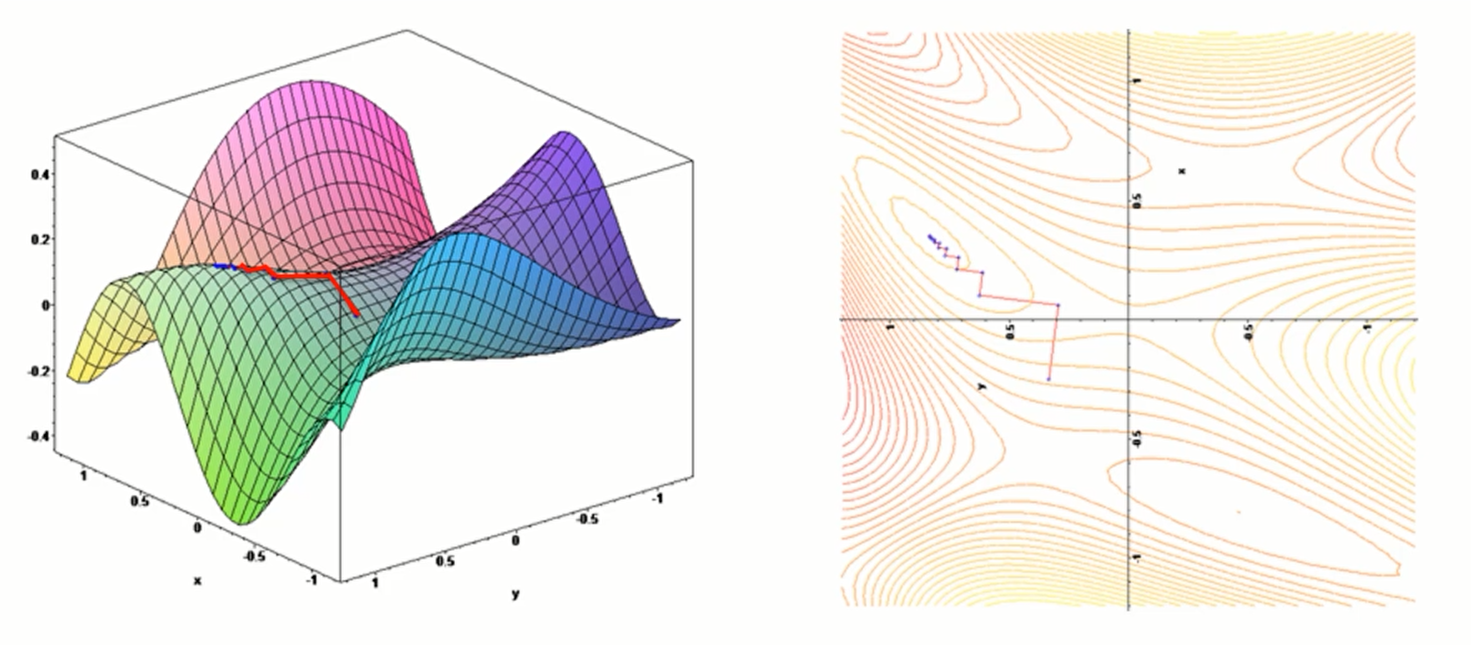
那么随机梯度下降是什么呢？

比如说我们现在的代价函数长这样：

因为我们可以选择不同类型的代价函数，所以长成这样也是有可能的。

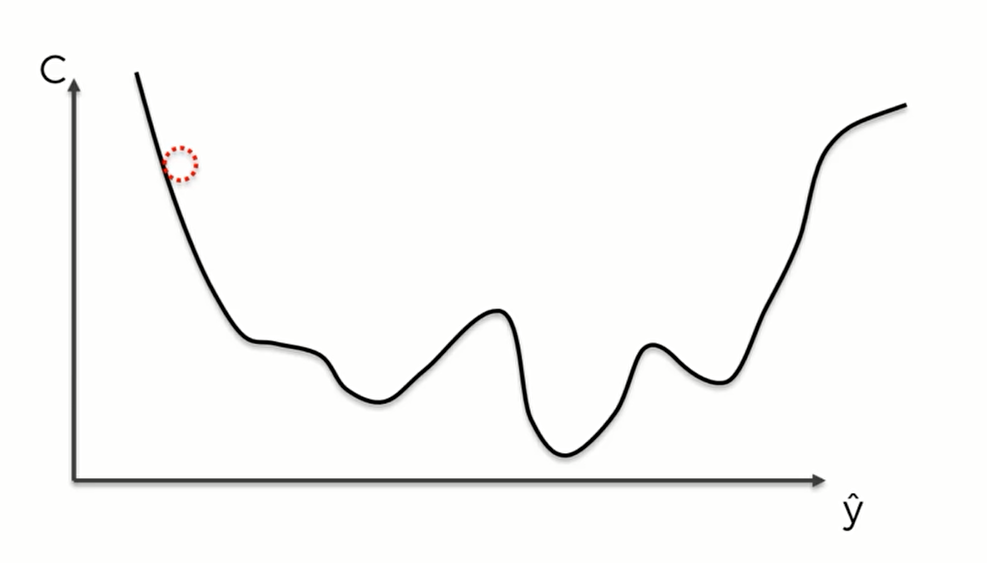
那么我们根据正常的梯度下降算法，很可能只找到了一个极小值，并没有找到整个函数的最小值。于是我们需要用随机梯度下降的方法来寻找最低点。对于批量梯度下降，我们将所有行的数据输入，才反馈一个值并更新我们的权重；但是对于随机梯度下降，我们则需要在每次输入一行的时候就反馈一个值并调整权重。

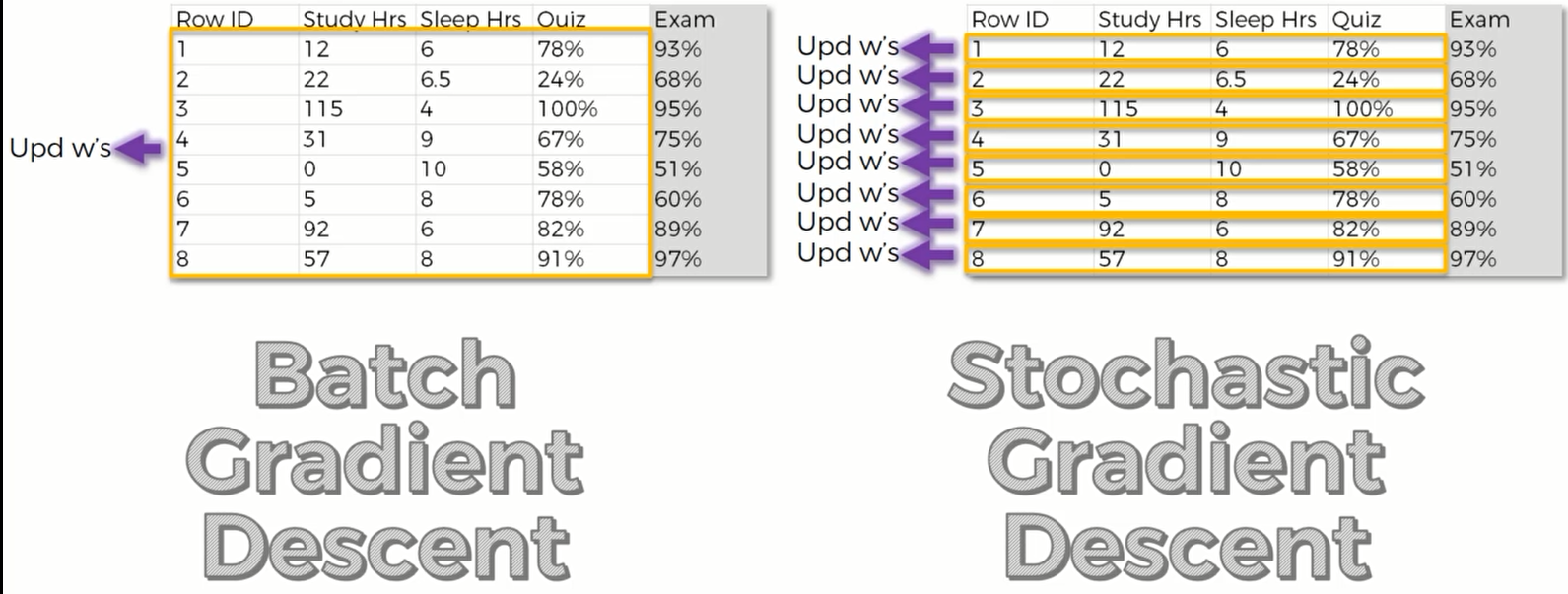
这样就可以帮助我们避免选择极小值。因为随机梯度下降它一次只对一行数据进行操作，具有更大幅度的波动，因此也更容易找到最小值。

具体设计数学的算法逻辑我将在吴恩达的机器学习课程笔记中记载，在这里就不再细说。

拓展文章：http://iamtrask.github.io/2015/07/27/python-network-part2/

http://neuralnetworksanddeeplearning.com/chap2.html

反向传播算法

我们之前说过 Forward Propagation(前向传播)，也就是信息进入输入层后，向前方传播以计算出 $\hat y$

那么当计算出代价函数之后，这个代价就会反向传播(Backpropagation) ,这样可以让我们来调整权重。

在这篇文章中，介绍了反向传播算法中的数学原理：http://neuralnetworksanddeeplearning.com/chap2.html

用随机梯度下降方法来训练人工神经网络的步骤：

  1. 随机初始化我们的权重，让他们接近于0但是不等于0

  2. 输入我们数据集的第一行数据到输入层，让每个特征都对应一个输入节点。

  3. 前向传播，从左到右,一直得到 $\hat y$

  4. 比较真实值和预测值，计算误差

  5. 使用反向传播算法，将误差传播回去。并对每一个权重进行调整

  6. 重复步骤一到五并对每行数据都更新我们的权重(强化学习)

  7. 当整个训练集数据都已经训练完毕，那么我们称这个神经网络为 epoch(一代)，我们要进行多代的训练，才能让神经网络模型将代价函数降到最小

项目实践

设置

首先我们导入一些包,我们需要用到numpy,tensorflow,datatime 和 fashion_mnist数据集。这个数据集，来自于kaggle ,网站是： https://www.kaggle.com/zalando-research/fashionmnist

这个数据集比较大，有七万多幅大小为28*28 的图像，每一张图像中的物品属于一类衣物，一共有10类衣物。分别是：

  • 0 T-shirt/top
  • 1 Trouser
  • 2 Pullover 套头衫
  • 3 Dress
  • 4 Coat
  • 5 Sandal 凉鞋
  • 6 Shirt
  • 7 Sneaker
  • 8 Bag
  • 9 Ankle boot

我们要做的就是用60000幅图像来训练我们的神经网络并用剩下10000幅当测试集交给神经网络去分类。

最后我们要做的是对测试集的测试结果进行一个评估

因为我们现在构建的是人工神经网络而不是卷积神经网络，神经网络的输入是一维的向量，但是这里我们要处理的对象是28*28的像素。因此我们会修改形状(reshape)，来讲28*28 的二维图像变形称为一个包括784个元素的一维输入向量

1
2
3
4
import numpy as np
import datetime
import tensorflow as tf
from tensorflow.keras.datasets import fashion_mnist

数据预处理

接下来，我们要把数据集设置成能被神经网络接受的格式，一共有4步：

loading the dataset

1
(X_train,y_train),(X_test,y_test) = fashion_mnist.load_data()

Normalizing the images

第二步，我们将图像归一化。我们将训练集和测试集中图像的每个像素除以最大像素数(255)。

这样，每个像素都将在[0,1]范围内。通过对图像进行归一化，我们可以确保我们的模型(ANN)运行得更快。

1
2
X_train = X_train / 255.0
X_test = X_test / 255.0

Reshaping the dataset

第三步，我们将图像变成一维向量的格式以便神经网络能够接受。因为图像的大小为28*28 所以我我们这样来写：

1
X_train = X_train.reshape(-1, 28*28)

其中，-1 代表了对所有元素都执行这个操作。

修改完后，X_train的形状从(60000,28,28) 变成了(60000,784)

构建人工神经网络

现在我们用Tensorflow来构建人工神经网络

Defining the model

我们先定义一个 Sequential 模型.(序贯模型)序贯模型是函数式模型的简略版，为最简单的线性、从头到尾的结构顺序，不分叉，是多个网络层的线性堆叠。

1
model = tf.keras.models.Sequential()

接下来我们来一个一个添加神经网络的不同层

Adding a first fully-connected hidden layer

第一个是全连接层。全连接层会拥有不同的超参数。因为在 神经网络中，除了寻找最优的权重和偏置等参数，设定合适的超参数也同样重要。比如各层神经元的数量、batch_size的取值、参数更新时的学习率、权值衰减系数或学习的epoch等。超参数寻找过程一般会伴随很多试错，所以用尽可能高效的方法找到超参数非常重要。 

1
2
3
4
5
model.add(tf.keras.layers.Dense(units=128,
								activation='relu', 
                                input_shape=(784, )
                               )
         )

我们用 model.add() 的方法来给我们的模型添加一个新的层。这里，我们添加的 fully-connected layer(全连接层)是一个Dense对象，在Dense类中我们又定义了三个参数：units即神经元的个数，activation即我们选择的激活函数，我们这里选的relu即rectifier activate function.(整流激活函数)。 第三个参数即输入参数的形状，input_shape =(784, )及说明这是一个包含了784个元素的向量，因为一幅图画的像素个数就是784。

Adding a second layer with Dropout

现在，我们要加入第二层，也就是Dropout层。dropout 是一种正则化技巧，我们会随机将一层中的神经元设为0。通过这种方法，一定比例的神经元会失活从而他们的权重不会再更新。我们添加dropout层就是决定了百分之多少的神经元会失活。这里，我们设置为0.2 意味着20%的神经元将失活

但这不是意味着失活的神经元就没用了，只是说每一次迭代，都只有20%的神经元会失活并停止学习过程，我们这样做的原因是为了避免神经网络过度学习导致过度拟合。因为在训练集上过度学习的画，在测试集上的结果就会很糟糕

1
model.add(tf.keras.layers.Dropout(0.2))

Adding the output layer

添加输出层，这个输出层也是一个Dense对象。即神经网络对图像预测的最后分类。

1
2
3
model.add(tf.keras.layers.Dense(units=10,
								activation='softmax')
		 )

因为 units =10 ,因为我们一共有10类衣服。这里我们使用的是softmax激活函数，因为我们希望通过神经网络来获得每一个类别的概率，利用softmax可以返回最高概率值的分类。

Compiling the model

现在我们已经完成了构造神经网络的基本步骤，接下来我们要编译这个模型，也就是将这个神经网络连接到一个优化器上(optimizer),并选择一个损失(loss)

这里，我们的优化器选择的是随机梯度下降算法(推荐)，loss就是预测值和目标之间的误差

因为这不是一个二元分类而是有10类，所以说，我们要填写metrics参数为sparse_categorical_accuracy

1
2
3
model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['sparse_categorical_accuracy'])
1
model.summary()

Training the model

编译好模型之后，我们加入数据，来训练神经网络，我们只要一行代码就能解决训练的问题。

输入训练集的X和y，并输入训练几代神经网络这三个强制参数即可。

1
model.fit(X_train, y_train, epochs=5)

我们看到随着代数的叠加，模型的准确率越来越高了。但这是训练集内部的准确率，并不是测试集的准确率，接下来我们就要将这个模型应用于测试集并对其进行一个评估

评估人工神经网络

1
test_loss, test_accuracy = model.evaluate(X_test, y_test)

loss: 0.3490

accuracy: 0.8736

1
print("Test accuracy: {}".format(test_accuracy))

Test accuracy: 0.8736000061035156

-------------本文结束，感谢您的阅读-------------