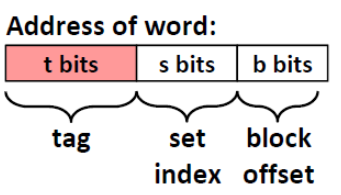
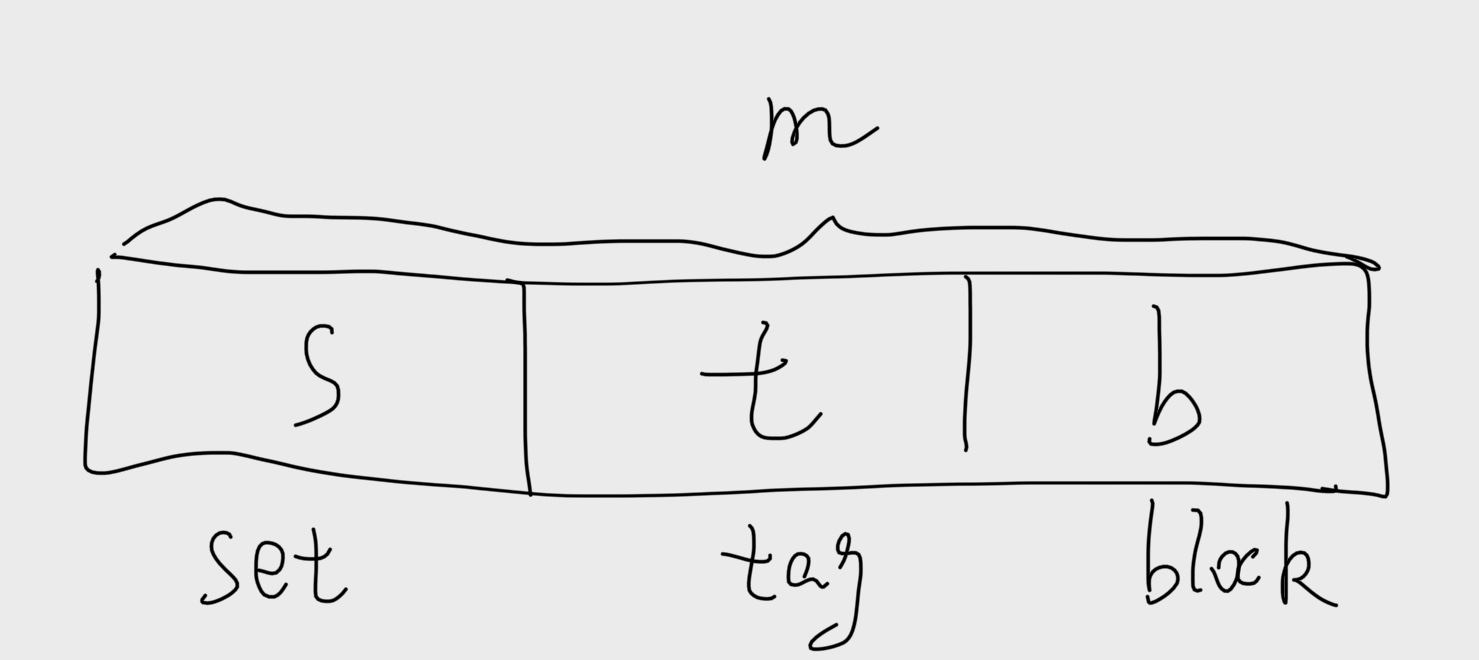
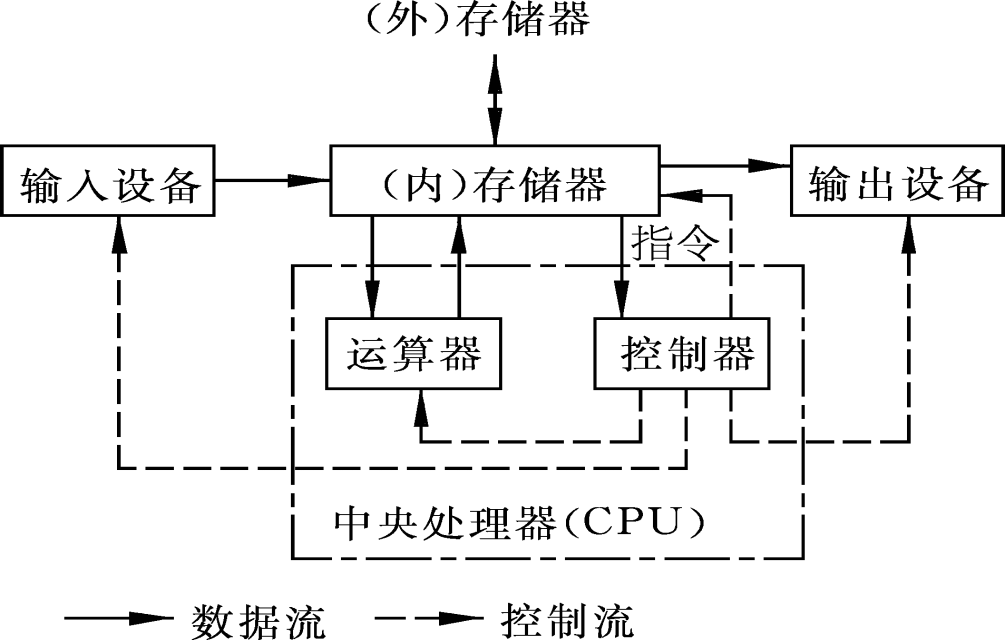
存储器层次结构(The memory hierarchy)
存储技术
磁盘
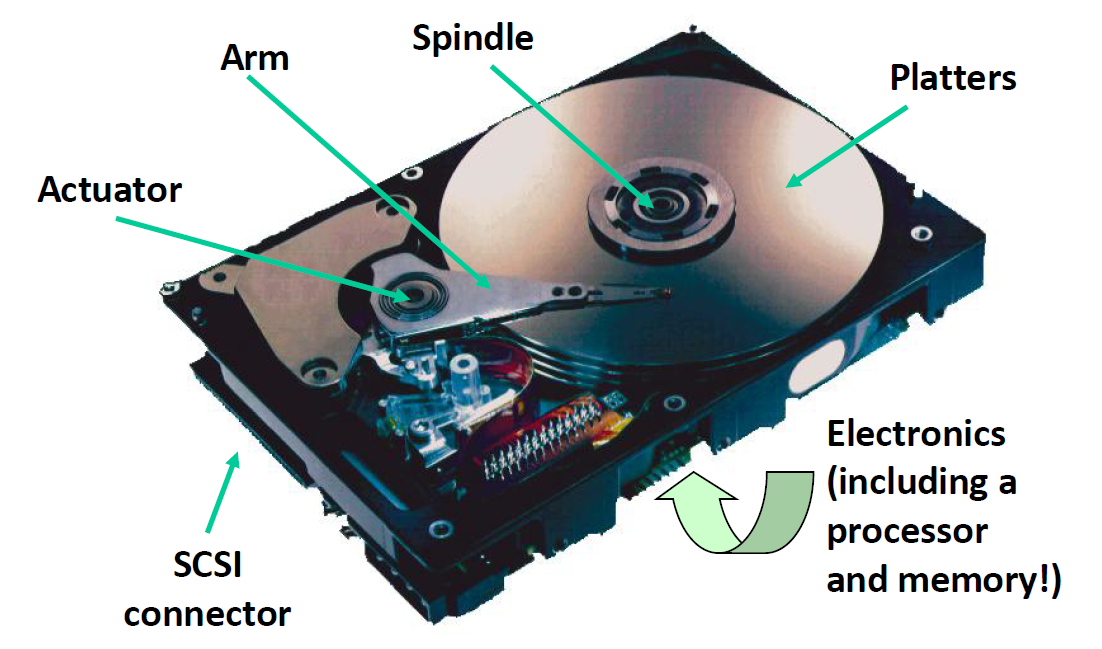
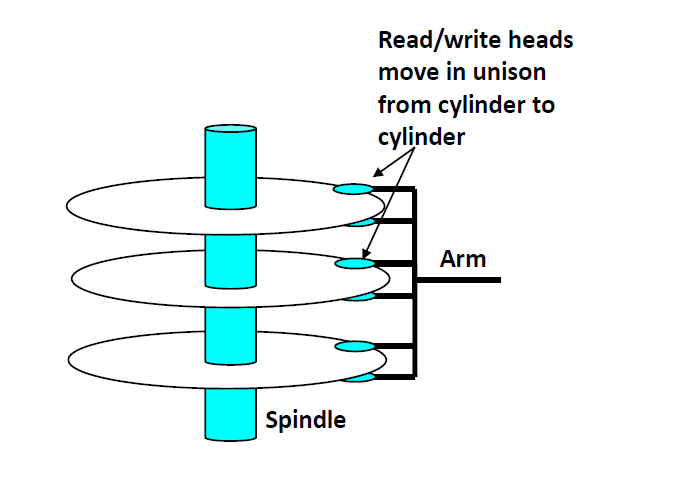
这是一个硬盘的内部结构,圆形的部分是磁片,Arm是磁头臂,其尖端就是一个磁头。
我们将磁盘模型抽象出来:
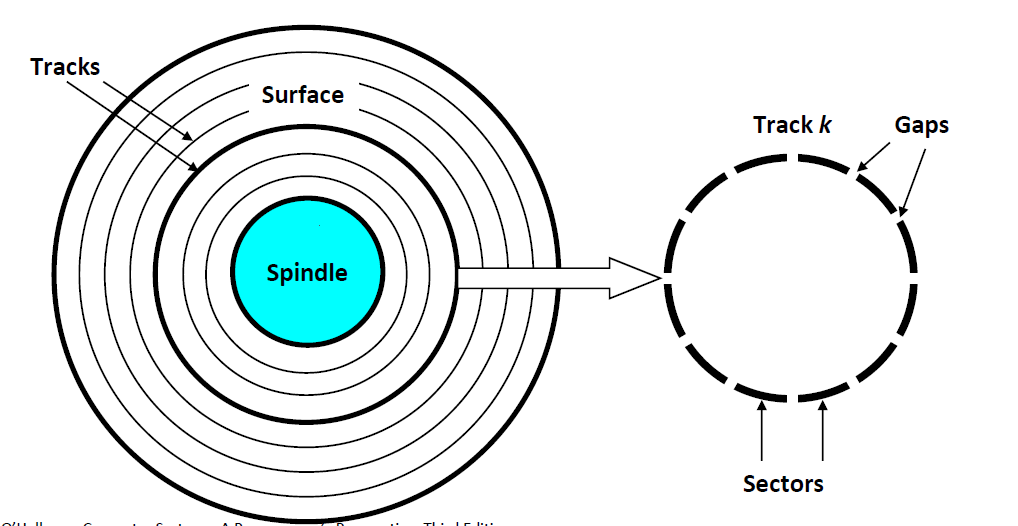
- 磁盘中有很多磁片,每一张磁片有2面
- 磁片的每一面又有若干的同心圆,叫做磁道(track)
- 磁道之间并不是连续的,中间有gap将其分成一小段一小段,每一小段叫做一个sector
磁盘容量
现在的磁盘都是以TB为单位来计算的
一张磁盘的容量和下面几个参数有关:
- Recording density
number of bits that can be squeezed into a 1 inch segment of a track.每英寸的sector可以放多少数据
- Track density
number of tracks that can be squeezed into a 1 inch radial segment.一张磁片上可以放多少磁道
- Areal density
product of recording and track density. 每平方英寸上可以放多少bity
磁盘操作
磁盘和磁头都可以运动。磁盘是转动,而磁头接近于径向移动。通过磁头径向移动,其可以扫到所有的磁道。在读取或者写入数据的时候,我们只要将磁头移动到特定的track上并旋转磁片,就可以通过电磁感应来讲数据写道特定的sector当中去。
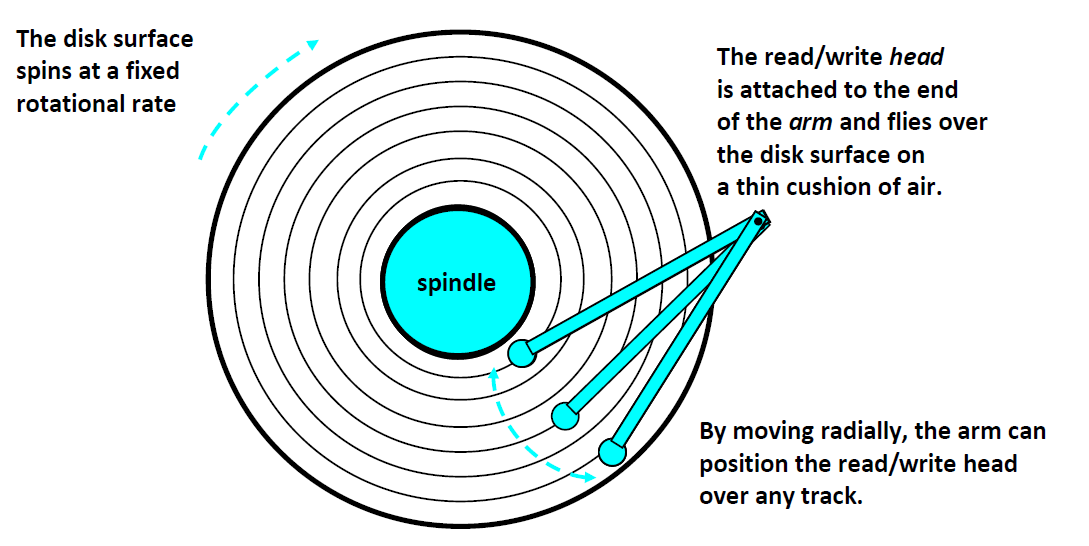
磁盘访问:
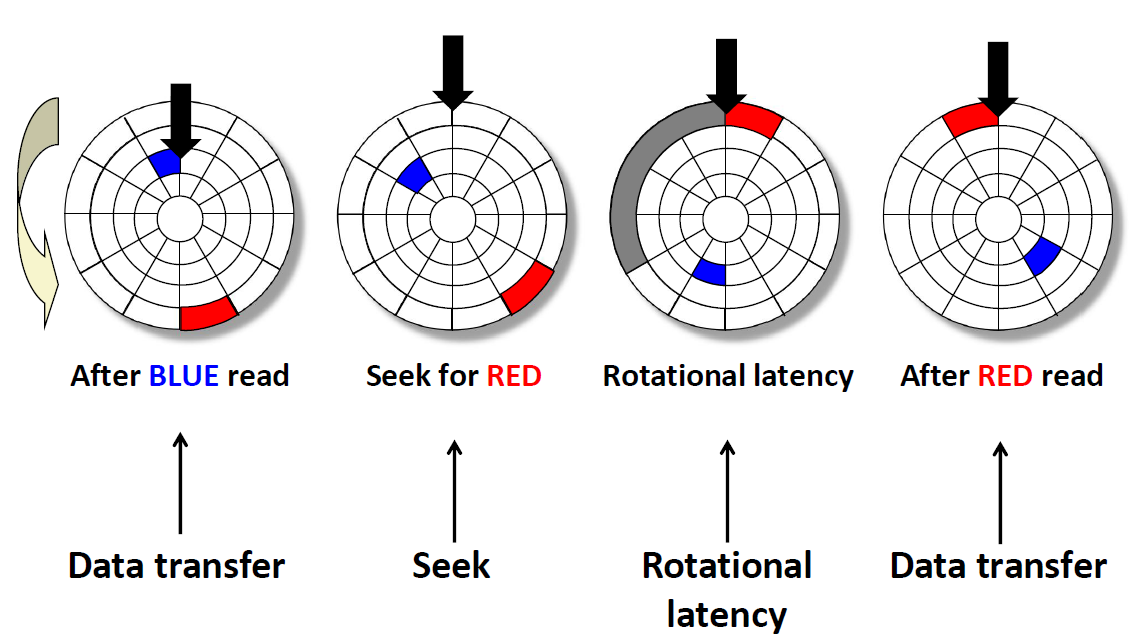
现在我们在访问蓝色的数据,访问完之后,如果我们要访问红色的数据,需要进行上述几个步骤。
首先,我们要将磁头移动到红色区域所位于的磁道上方,(抬起来移动过去),这个过程叫做 seek(寻道)、
接下来,我们要将磁片旋转,让红色区域转到磁头的下方,这个过程叫 Rotational latency
最后,我们的磁头要碰到红色区域进行电磁感应并传输数据
这些过程,都是机械运动,所以相对于内存来说,磁盘访问是非常非常慢的。
访问时间
我们来计算一下磁盘访问时间。 简单来说 就是上面几个过程的所消耗时间之和,也就是寻道时间+旋转时间+传送时间
$T{access} = T{avg~seek}+T{avg~rotation}+T{avg~transfer}$
寻道时间通常为3~9ms,一次寻道的最大时间 $T_{maxseek}$可以高达20ms。
旋转时间是的计算公式为 $T_{avg~rotation}= \frac{1}{2}\times\frac{1}{RPM}\times\frac{60s}{1min}$ RPM即为每分钟的转速
传送时间一般依赖于旋转速度和每条磁道的扇区数目。因此我们可以这样来计算
$T_{avg~transfer} = \frac{1}{RPM}\times\frac{1}{(平均扇区数/磁道)}\times \frac{60s}{1min}$

估计访问下面这个磁盘上一个扇区的访问时间(以ms 为单位):
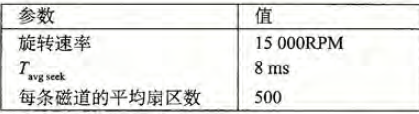
$T{avg~rotation} =\frac{1}{2}\times T{max~rotation}=\frac{1}{2}\times\frac{60s}{15000RPM}\times\frac{1000ms}{1s}= 2ms$
$T_{avg~transfer}=(60s/15000RMP)\times\frac{1}{500扇区/磁道}\times\frac{1000ms}{s}= 0.008ms$
所以预计总的访问时间为 $8+2+0.008 \approx10ms$
硬盘两个参数很重要:随机访问速度和连续访问速度。硬盘的随机访问速度是很慢的,但是连续访问速度是很快的。当我们写的随机算法将内存中的空间占满之后,数据便要随机存储到硬盘当中去,这时候磁盘的随机访问速度如果很慢那么这个算法肯定是会垮掉的。
比如说这一题:假设1MB 的文件由512 个字节的逻辑块组成,存储在具有如下特性的磁盘驱动器上:

对于下面的情况,假设程序顺序地读文件的逻辑块,一个接一个,将读/写头定位道第一块上的时间是 $T{avg~seek}+T{avg~rotations}$
A. 最好的情况: 给定逻辑块道磁盘扇区地最好的可能的映射(顺序的),估计读取这个文件所需要的最优时间
B. 随机的情况:如果块是随机映射到磁盘扇区的,估计读这个文件所需要的时间,以毫秒为单位
首先我们计算 $T{access}=T{seek}+T{avg~rotation}+T{avg~transfer}=5ms+\frac{1}{2}\times\frac{60}{10000}\times\frac{1000ms}{1s}+\frac{60s}{10000RPM}\times\frac{1}{1000扇区/磁道}\times\frac{1000ms}{1s}\approx 8ms$
如果是最好的情况,块被映射到连续的扇区,在同一柱面上,那样就可以一块接一块地读取,不用寻道和移动读写头。一旦读/写头定位到了第一个扇区,我们只需要旋转磁盘2整圈(每圈1000个扇区,每个扇区512字节)来读取2000个块。所以读取这个文件地总时间只要 $T{seek}+T{avg~rotation}+2\times T_{max~rotation}=5+3+12=20ms$
随机的情况下,块被随机地映射到扇区上,读2000块中的每一块都需要 $T{avg~seek}+T{avg~rotations}$ms = 8*2000=16000ms=16秒
所以,我们看得到,清理磁盘碎片是一件很重要的事情!
I/O Bus
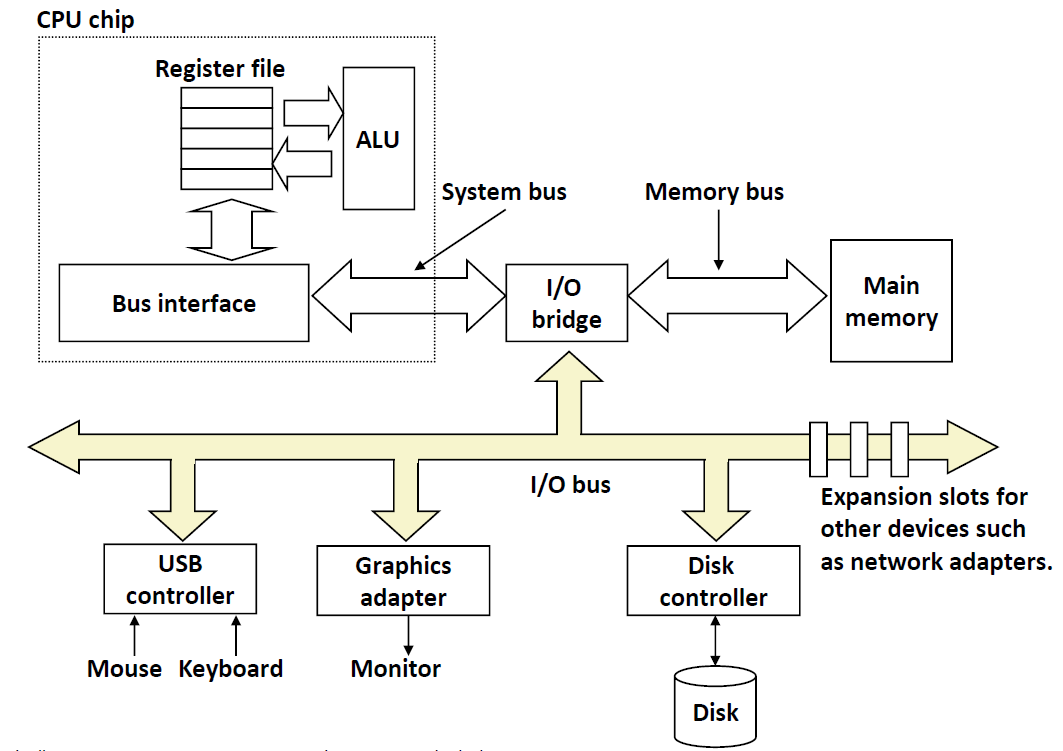
磁盘是挂在磁盘控制器上的,而磁盘控制器是挂在I/O Bus,与I/O bridge相连的。那么我们要读取disk中的sector的话,首先要告诉磁盘控制器,然后从磁盘中取出数据后,直接放入内存而不经过CPU的。这种模式叫做 DMA(Direct Memory Access) 直接内存访问。
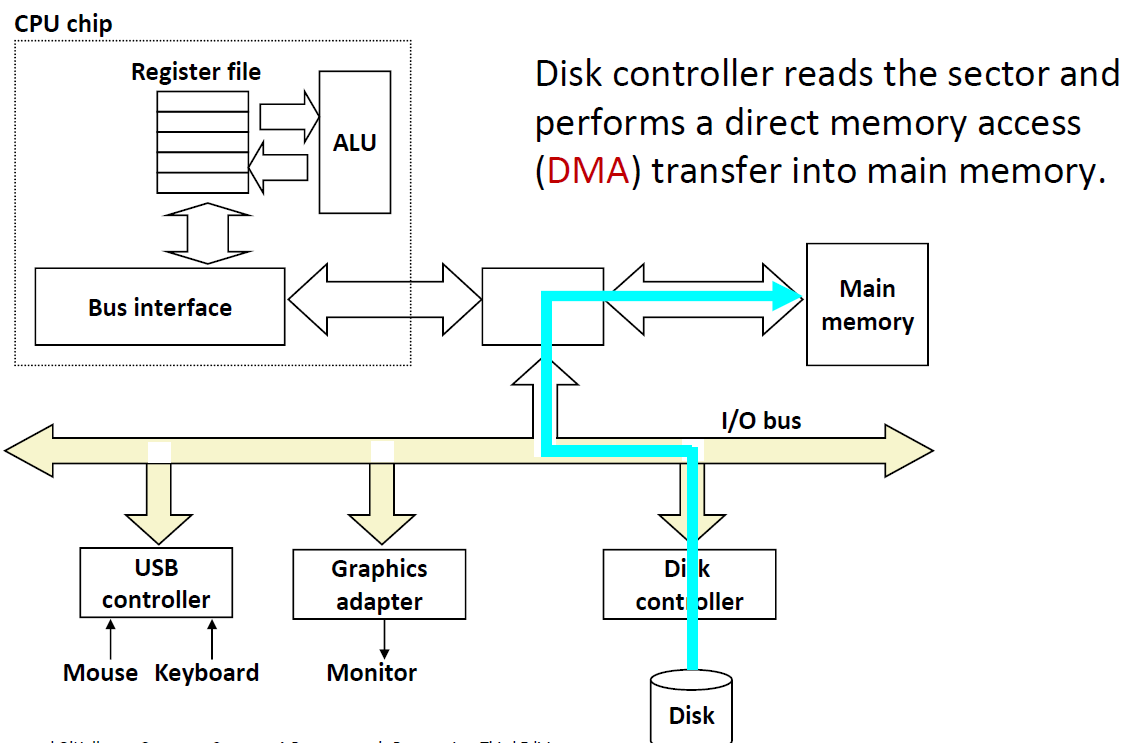
那么为什么不用CPU去取数据呢?因为CPU是一个很贵的”劳动力“,而取数据是一个相对比较低端的”杂活”,我们要让CPU去干更加复杂的计算。
Nonvolatile Memories
DRAM和SRAM都是易于丢失的内存,停电之后,里面的数据都没了
非易失的内存,在停电之后,数据并不会丢失
- Read-only memory (ROM): programmed during production
- Electrically eraseable PROM (EEPROM): electronic erase capability
- Flash memory: EEPROMs, with partial (block-level) erase capability (U盘)
- 3D XPoint (Intel Optane) & emerging NVMs
非易失的数据,有这些应用:
- Firmware(固件) programs stored in a ROM(比如Bios,磁盘控制器,网卡,显卡加速器等)
- 固态硬盘(ssd)
- Disk caches
SSD(固态硬盘)
固态硬盘的结构如下:
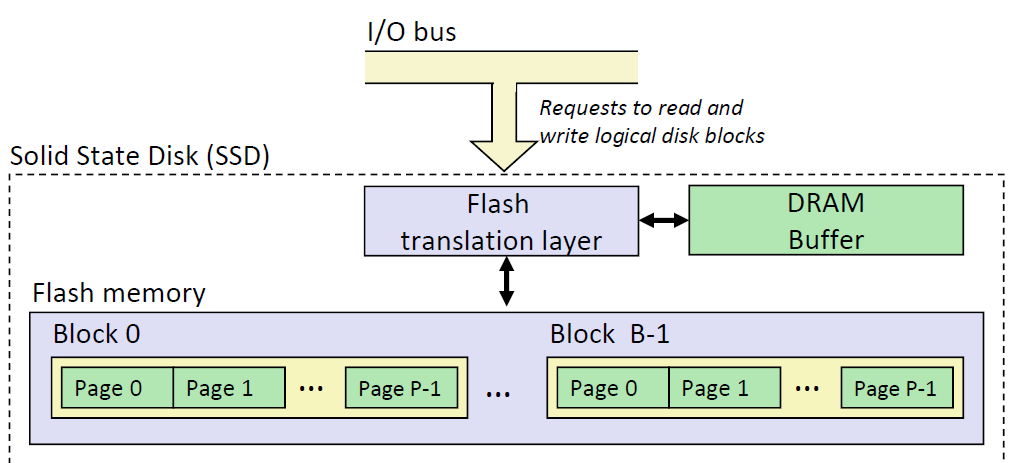
SSD中,有很多Block,每个Block之间又有很多Page
- 每一个Page的大小从4k-512k不等,每一个Blocks又有32-128个page
- 读和写都是以page为单位进行的
- 不能只写1个page,需要把整个block擦除之后再写
- 每一个block的寿命大概是写入十万次
ssd的性能

顺序的读取:2G出头,顺序的写入:2G不到一点。但是随机读和随机写入相对于顺序的读取和写入慢很多很多。随机的写入特别慢,因为我们先要擦除block,再写入。
我们这里还要了解一Buffer和Cache的区别
Cache是缓存,一般认为Cache中有的,比它第一级的存储区域也要有。cache是其下一级的一个子集
Buffer是缓冲,我们将一些数据暂时放到Buffer中,但Buffer中的数据可能并不会在低一级的存储器中。相当于一个蓄水池。
SSD中的DRAM是个Buffer,因为我一下子要将东西写入page中是不方便的,所以我们暂时把数据放到蓄水池Buffer当中。
还有一个作用,Buffer是将随机的数据,变成连续的数据,这样可以提升写入速度,同时也付出了昂贵的DRAM造价
局部性
局部性对硬件和软件系统的设计和性能都有着极大的影响,有良好局部性的程序比局部性差的程序
运行得更快。因此一个编写良好的计算机程序常常具有良好的局部性。也就是说它们倾向于 引用 邻近于 最近引用过的数据项 的数据项,或者是最近引用过的数据项本身。
局部性常常有两种不同的形式:时间局部性和空间局部性。
时间局部性良好是说,被引用过一次的内存位置很可能再不远的将来再次被多次引用
空间局部性良好是说,如果一个内存的位置被引用了一次,那么程序很可能在不远的将来引用附近的一个内存位置。
对于一个同一个算法来说,调换两行遍历代码并不会影响算法的复杂度,但是其局部性可能相差会非常非常大。比如说一个二维数组元素求和的算法.正常来说我们写双重循环,内层循环会读一行数据,外层循环则负责换行。因此这个 sumarrayrows 算法具有良好的空间局部性,因为他按照数组被存储的优先顺序来访问这个数组。
1 | int sum_array_rows(int a[M][N]) |
算法得到了一个很好的步长为1 的引用模式,具有良好的空间局部性:

但是我们只要做一个很小的改动,就会对其局部性有很大的影响。比如说我们把循环中的i、j和M、N调换
1 | int sum_array_cols(int a[M][N]) |
那么这样的交换就会导致这个算法的空间局部性很差,因为他按照列顺序来扫描数组,而不是按照行顺序,因为在C数组再内存中是按照行顺序存放的。
我们得到了一个步长为N的引用模式,如图所示:

我们再来举一个例子:
一个对三维数组求和的算法如下:
1 | int sum_array_3d(int a[M][N][N]) |
我们看到,三层循环是按照i、j、k来执行的的,但是 我们最后访问的却是a[k][i][j]这显然是一个局部性很差的算法,因为其步长是N*N*sizeof(int) ,我们需要调整一下循环的顺序来将这个算法的步长改为1——将第二层关于j的循环放在最内层即可。
最后,让我们讲一些评价程序中局部性的一些简单原则:
- 重复引用相同变量的程序有良好的时间局部性
- 对于步长为k的引用模式的程序,步长越小,空间局部性越好。在内存中以大步长跳来跳去的程序空间局部性会很差。
- 对于取指令来说,循环有好的时间和空间局部性。循环体越小,循环迭代次数越多,局部性越好。
存储器层次结构
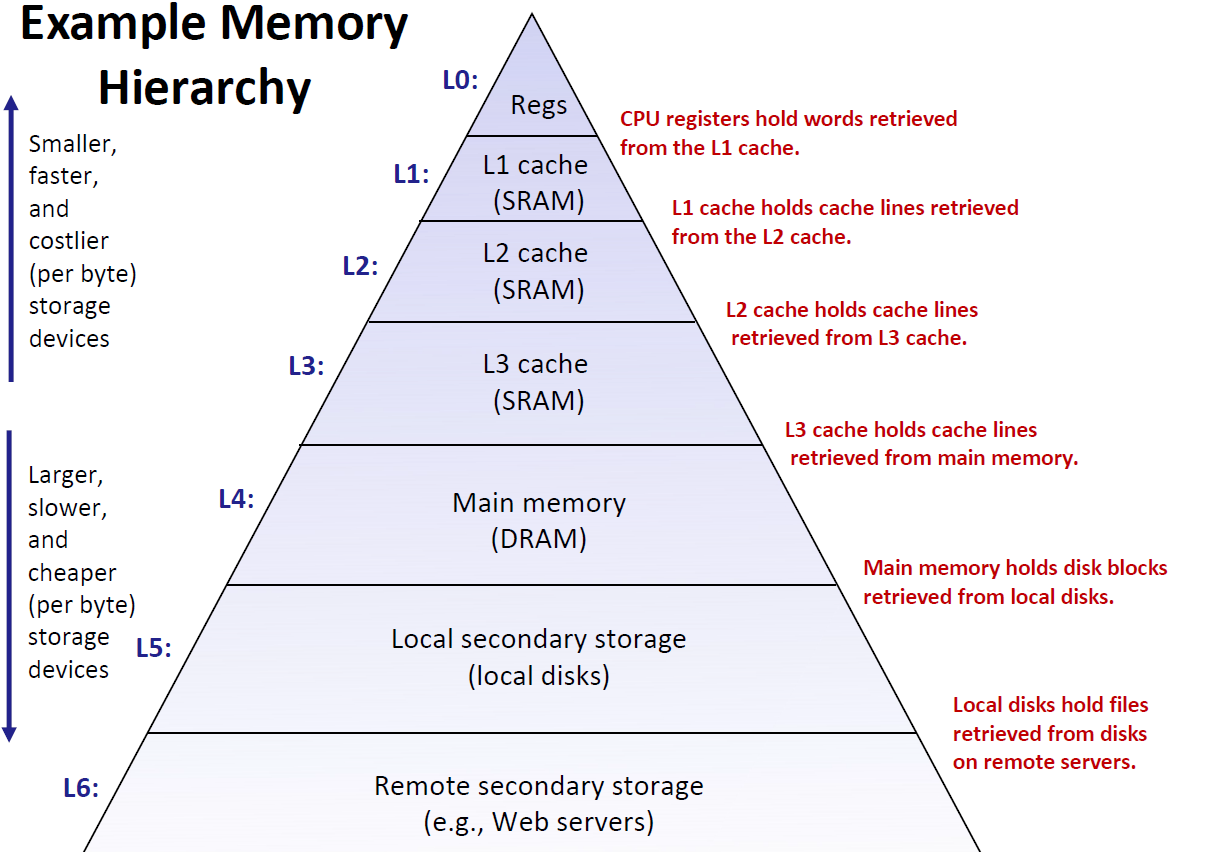
我们的存储器大致可以画成一个金字塔形,越上面的造价越贵、读取方式越快、容量越小;相反的,底层的存储设备变得更慢
在最高层(L0) 是少量快速的CPU寄存器,CPU 可以在一个时钟周期内访问它们。
接下来是一个或多个小型到中型的基于SRAM 的高速缓存存储器,可以在几个CPU 时钟周期内访问它
们。这些元器件发热量高耗电大,因此没有办法造的很大。这里我们设计了3层Cache然后是一个大的基于DRAM 的主存,可以在几十到几百个时钟周期内访问它们,
接下来是慢速但是容量很大的本地磁盘。
最后,有些系统甚至包括了一层附加的远程服务器上的磁盘,要通过网络来访问它们
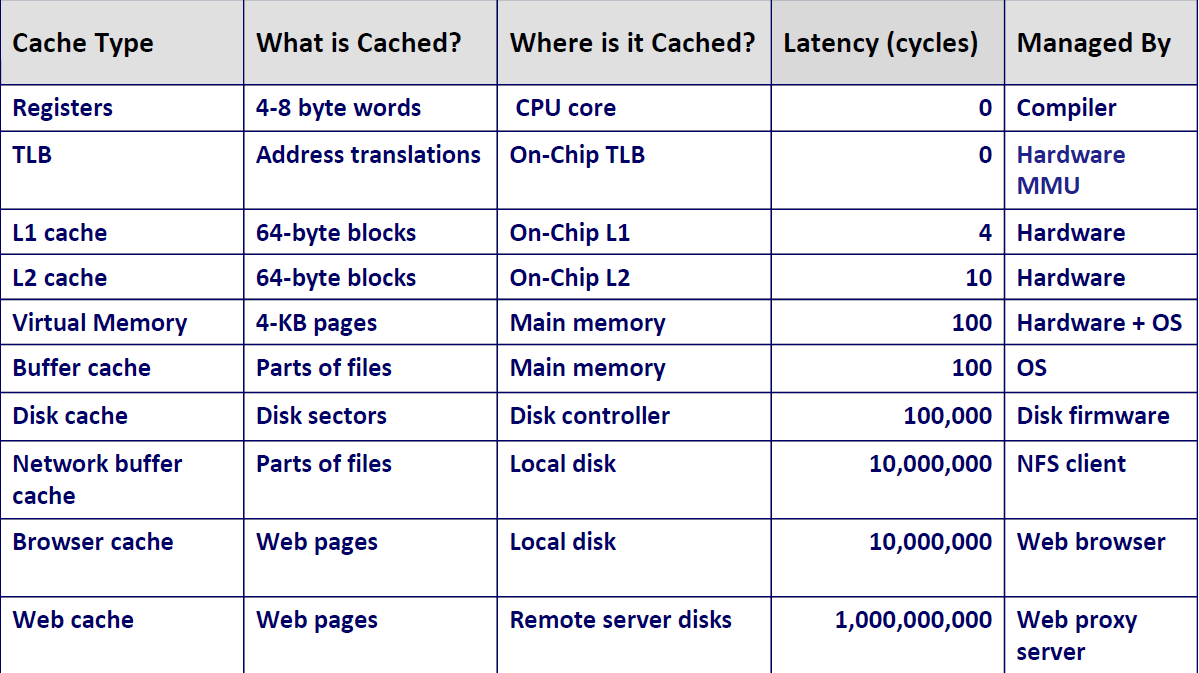
对于Cache,我们是一行一行读入的,每一行是64个字节
对于磁盘,我们会读取相当大的一块区域,而且磁盘跳读是非常慢的。
我们知道,现在的CPU读取和磁盘读取的速度相差地越来越大,我们希望用便宜的价格买到大容量存储的设备,又希望在读取时能达到一个较高的速度,怎么办?这时候Cache就应运而生了, 在运行程序的时候,我们希望将我们需要的数据放在靠近金字塔顶端的Cache中,把我们不要的数据放在底层磁盘当中。这样,只有在进行数据交换的时候,才会到磁盘当中去取,时间才会变慢。
这就好像一个贪心算法,根据局部性原理,当我们访问过一个数据之后,我们就可以将其放在上层cache中,因为将来很可能再会用到。也就是说,上层是下层的缓存。
存储器层次结构中的缓存
一般而言,高速缓存(cache)是一个小而快速的存储设备,它作为存储在更大、也更慢的设备中的数据对象的缓冲区域。使用高速缓存的过程称为缓存(caching)
存储器层次结构的中心思想是,对于每个k,位于為层的更快更小的存储设备作为位于k+1层的更大更慢的存储设备的缓存。换句话说,层次结构中的每一层都缓存来自较低一层的数据对象。
比如说这个例子,第k层更小更快也更贵,其只有4个块,缓存着第k+1层块的一个子集。k+1层存储器被划分为16个大小固定的块,编号为 0~15
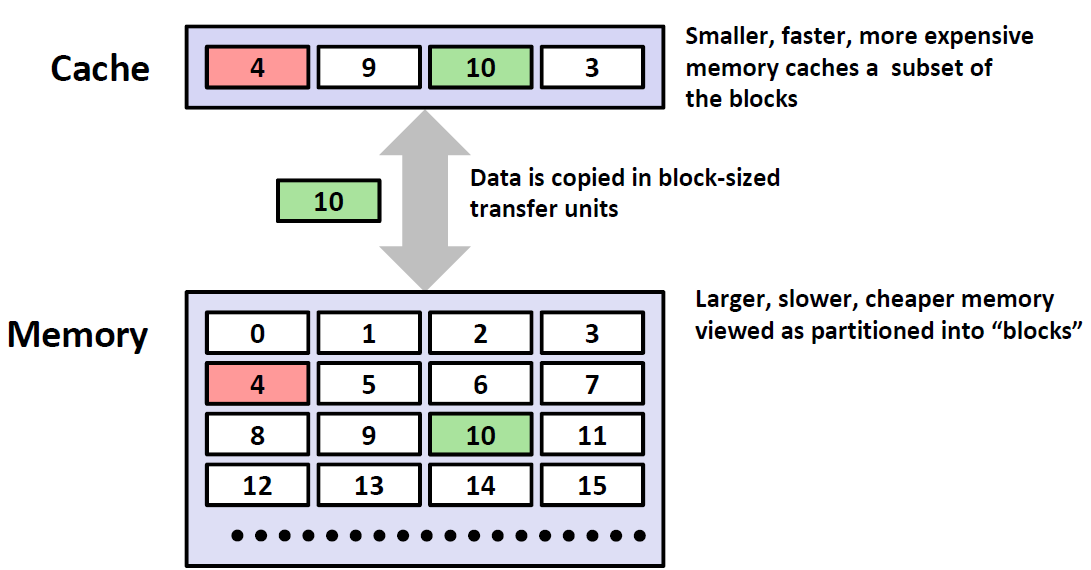
Hit
接下来我们来介绍一个概念: Hit 命中.简单来说,就是上一级想要的数据,下一级刚好有。比如下面这个例子,顶层的想要数据14,然后发现Cache里面刚好有数据14,那么这就是命中了。
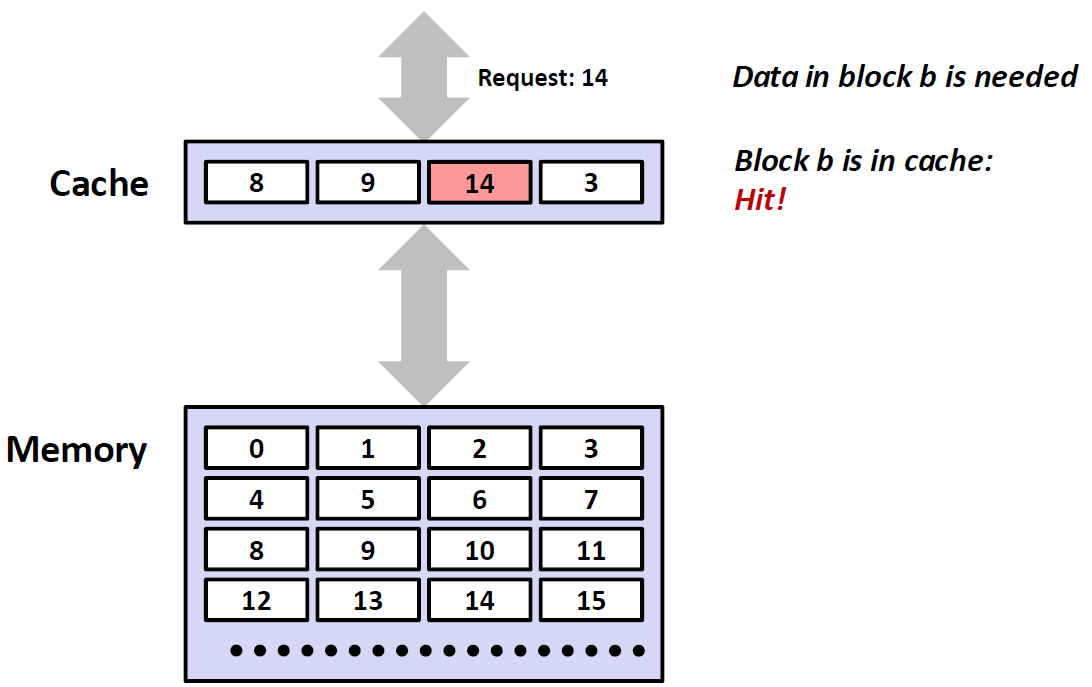
Miss
Miss和Hit相反,也就是说没有命中。比如下面这个例子,上面的数据想要12,而第二层Cache中原来的数据为8、9、14、3并没有12,所以这就是一个Miss。于是Cache又要向下一层Memory里去找数据12,Memory里有12,然后将其提到Cache中去。
那么这就出现了一个问题:我们怎么来决定什么元素应该被替换(上面这个例子中,9被替换)? 也就是说找到一个Victim。这是在操作系统中要学习的内容,也就是 Replacement policy,也是我们规定的一套标准。
3 Types of Cache Misses
我们要知道 ,程序出现了Miss的话,要再向下级去寻找,这就导致运行时间长了很多,是一种严重拉低效率的情况。
Code (compulsory) miss
顾名思义,就是冷启动。因为我们电脑启动的时候,Cache里面是没有数据的,因此第一次肯定会miss。
所以也说这是 compulsory miss
Capacity miss
Capacity是容量之意,比如说,我每一次循环里面要读取的数据时4个kb,但是一个cache里面的容量只有3k,那么不管怎么访问和优化,都会出现miss的情况。有点捉襟见肘的意思。
容量不够的话,我们可以停止一些程序的运行,以确保急需cache的程序来访问内存。
Conflict miss
举一个例子,假设我们规定,在k+1层的编码为i的block 必须被放到k层编码为(i mod 4) 的block当中,而我们又必须反复去读取0,8,0,8这一串数据,那么虽然说我k层的blocks还没有用完,capacity也是够的,但是每次访问还是会出现miss,因为0,8 mod4都是0,被映射到了同一个对应的block,造成了conflict miss。因此,这种情况是我们需要规避的,我们需要设计良好的机制来减少甚至避免这种情况的发生。
Cache Memories(高速缓存存储器)
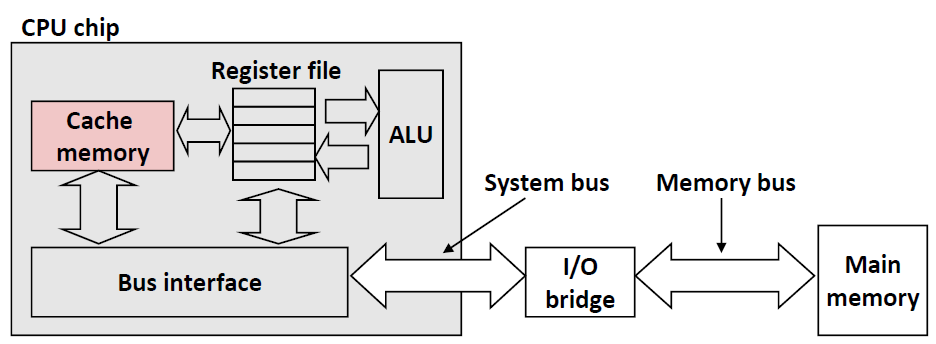
这就是Cache在CPU中的模拟结构。CPU会首先在cache memory中去找。
下面这幅图是Instruction Cache在CPU中的一些具体的功能
Fetch Control 是决定取哪一条指令的,然后再到Cache中去取。
Instruction Decode 是将从Cache中取回来的指令变成二进制编码的
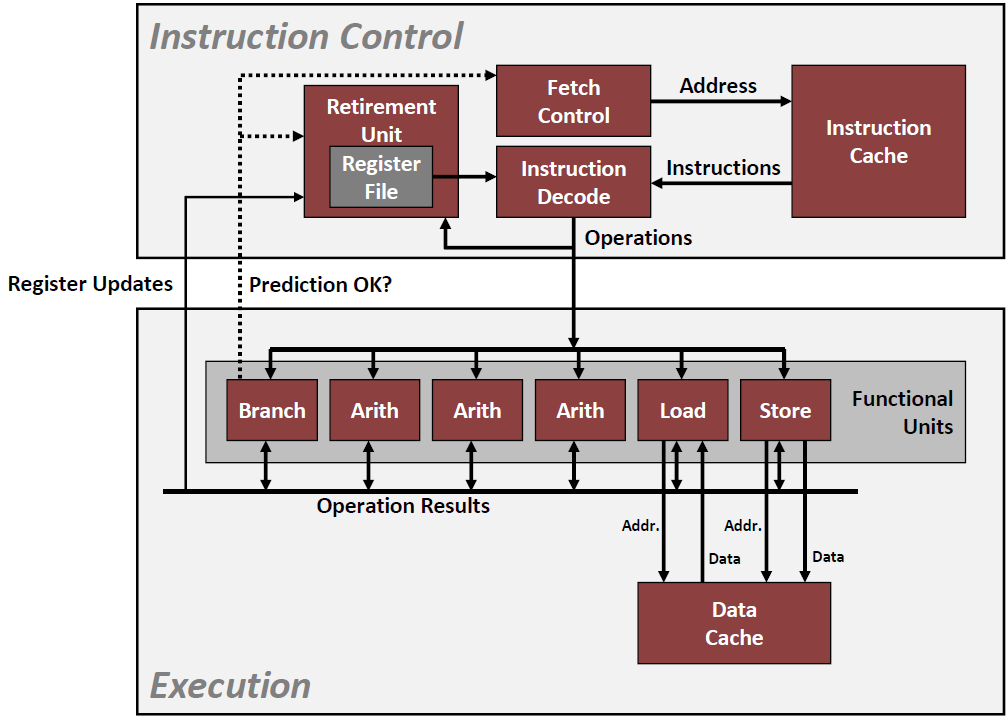
General Cache Organization
cache memory是这样来组织的:
一个cache里面有若干个set,每个set里面又有若干的cache line。 一个cache里面,有$2^s$个sets,每一个sets里面又有 $2^e$个cache line。这样做的目的是为了编码比较方便。
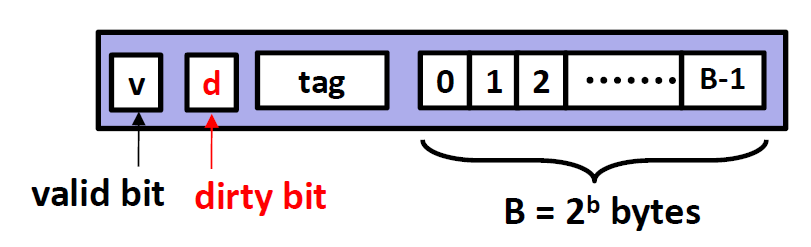
每一个cache line内部又分成三个部分,分别是 v,tag和B。
B就是Cache line里面的存储空间,大小为 $2^b$个 bytes
v只有一位,全称为 valid bit,来标志这个cache line 是否有用。
- tag则是这个cache line的标签。
现在我们来做一个小练习:
我们得到了表格中的一部分信息,我们现在要讲表格补齐,因此这里我们需要对地址的划分非常清楚
| 高速缓存 | m(位数) | C(cache大小) | B(块大小) | E(cache line总数) | S(Set总数) | t(tag位数) | s(set位数) | b(block位数) |
|---|---|---|---|---|---|---|---|---|
| 1 | 32 | 1024 | 4 | 1 | ||||
| 2 | 32 | 1024 | 8 | 4 | ||||
| 3 | 32 | 1024 | 32 | 32 |
C代表了Cache Size 也就是 $S\times E\times B = 1024$ 这里我们已经知道了B和E,于是我们可以先填写S。
- 第一个cache 的$S = 1024/4 = 256$,也就是说这个Cache 有256个set
- 同理,第二个Cache的$S = 1024/(8\times 4) = 32$ ,也就是说这个Cache 有32个set
- 第三个Cache的$S = 1024/(32\times 32) = 1$,也就是说这是一个全相连的Cache,只有一个Set
- 知道了 S之后,我们可以根据 $S = 2^s$ 求出小s的值,小s的值即地址空间关于定位Set的位数
- 知道了B之后,我们可以根据 $B = 2^b$ 求出小b的值,小b的值即地址空间关于定位block偏移量的位数
- 知道了 s和 b之后,我们就可以知道 t的值,因为$t= m-s-b$ 其中m为地址的总位数,因为地址的总位数只由三个部分 t,s,b组成。
| 高速缓存 | m(位数) | C(cache大小) | B(块大小) | E(cache line总数) | S(Set总数) | t(tag位数) | s(set位数) | b(block位数) |
|---|---|---|---|---|---|---|---|---|
| 1 | 32 | 1024 | 4 | 1 | 256 | 22 | 8 | 2 |
| 2 | 32 | 1024 | 8 | 4 | 32 | 24 | 5 | 3 |
| 3 | 32 | 1024 | 32 | 32 | 1 | 27 | 0 | 5 |
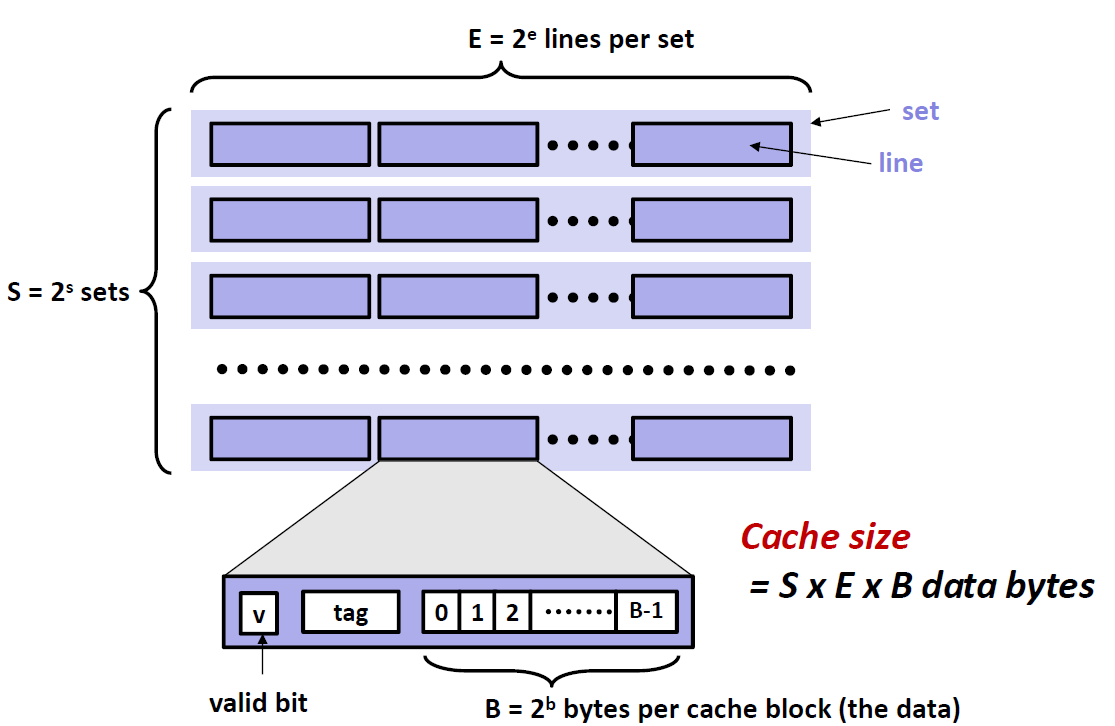
读取Cache
示意图如下:
现在拿到了一个地址,机器不会直接去内存里去找地址,而是先会在Cache里面寻找,寻找流程如下:
一串地址可以分成三个部分:tag + set index + block offset(偏移量)
- 首先利用set index位来定位这串地址在cache中位于哪一个sets,因为一共有$2^s$ 个sets,所以我们需要用 s位来当我们的索引
- 在定位到的set中,遍历所有的cache line,查找是否有和我们地址中 tag段相匹配的 cache line
- 如果找到了这个cache line,并且这个cache line是valid ,那么就说命中cache了
- 最后通过我们的offset定位到特定的数据
定位 set $\Rightarrow $ 匹配tag $\Rightarrow$ 找到byte
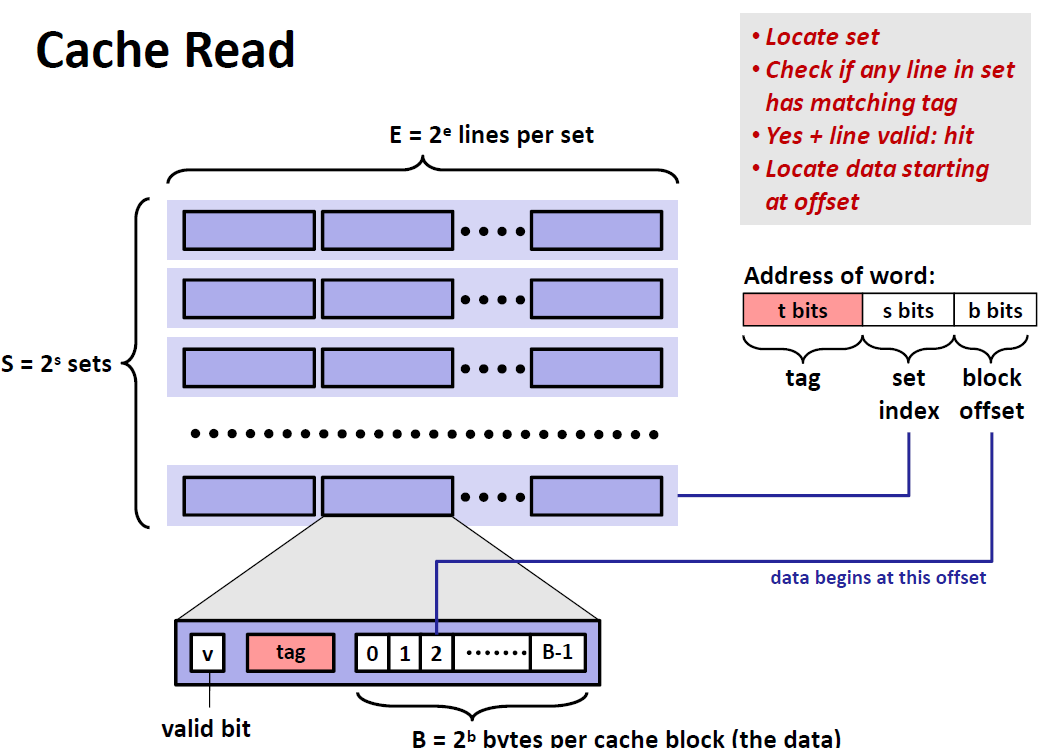
Direct Mapped Cache(E=1)
当E等于1的时候,每一个set只有1条cache line,这时这种cache也被称为是 Direct Mapped Cache。假设每个cache line 中的block size B 为8 bytes.那么这个cache的模型就如下图所示:
这种Cache的查找模式如下:
我们定位到set之后,我们去看tag是否与cache line中的tag相匹配,还要看这个cache line是否valid。同时满足两个条件才能说命中了。如果一开始tag就不匹配,那么这个cache line就是victim,我们要删除它并替换掉。
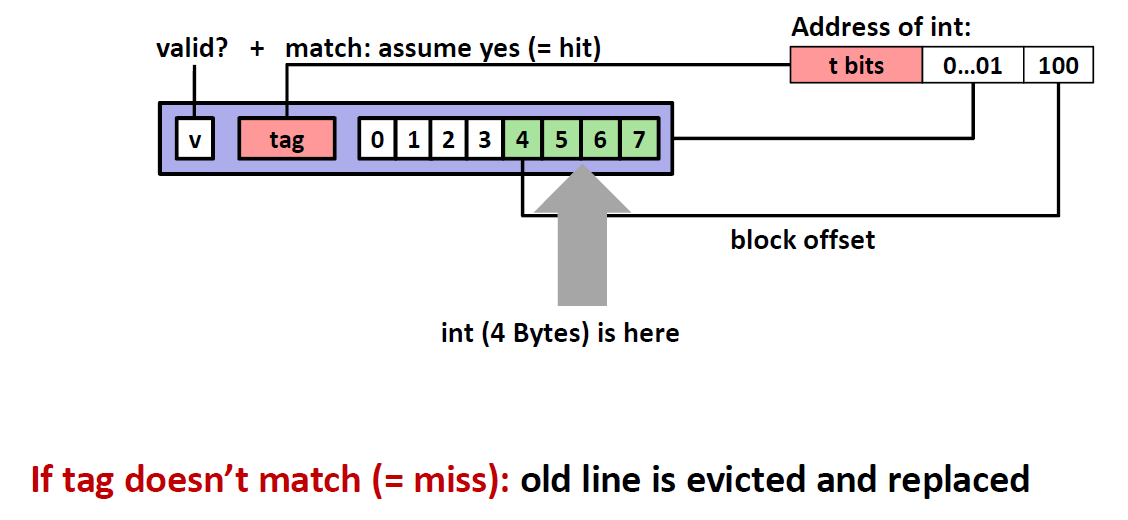
下面是一个模拟的查找情景。我们有一个4位的地址,cache中有4个sets,每一个sets中有一个cache line,每个cache line的Block 空间为 2 bytes 。block里面存放的数据,就是查找地址指向的数据 。
查找地址左边一列是地址所代表的十进制数,查找不成功的时候,我们会将这个地址指向的数(前/后两个)放到blocks当中去。
那么我们查找的第一行是 $[0000_2]$ ,所以应该映射到第0个set,这时候cache是空的,所以是cold miss,然后将这个数据0存储到第一行cache line当中,因为一个cache line可以存储两个bytes,所以我们在将0输入的时候同时也要将0后面的数字1也一并输入
第二行是$[0001_2]$ ,映射到第0个set,这时候cache line是有数据的,然后我们看tag也适合cache line相匹配的,于是这一个地址是 Hit
第三行是$[0111_2]$ ,定位到set3,显然这时候cache line是空的,那么就是 cold miss
第四行是$[1000_2]$, 定位到set0,tag不匹配,所以miss,并且将set0作为victim,将其替换成 $v=1,Tag=1,M[8-9]$
第五行是$[0000_2]$ ,定位到set0,tag又不匹配,所以miss,并且将set0作为 victim,将其替换成$v=1,Tag =0,M[0-1]$

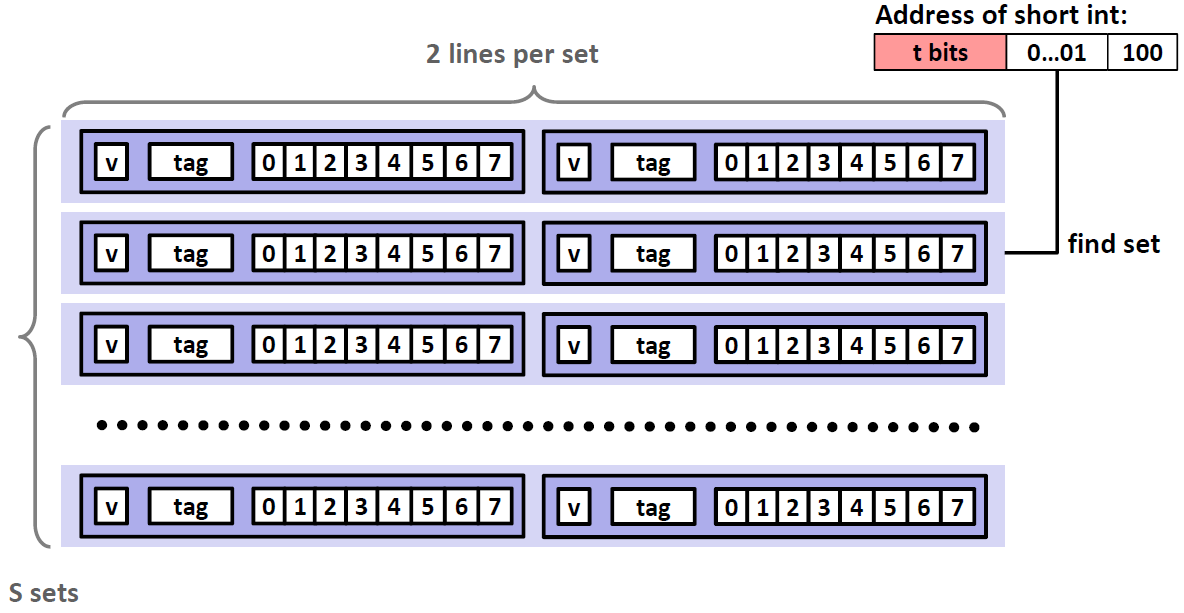
E-Way Set Associative Cache 组相连的cache
顾名思义就是说一个set当中有多个cache line,这里取 E=2,每个cacheline当中有8个bytes
那么查找的过程如下:
首先还是找到对应的set
其次同时比较两个cache line 的tag,匹配到哪个进入那个cache,如果两个都不匹配,就是miss,这时候要在两个cache line里面选择一个杀掉
选择哪个cache line有多种方法,可以是随机的,也可以是least recent used(LRU),即最近最少使用的cache line。但是最近最少使用实现起来没有那么简单,如何高效实现是一件比较复杂的事情。
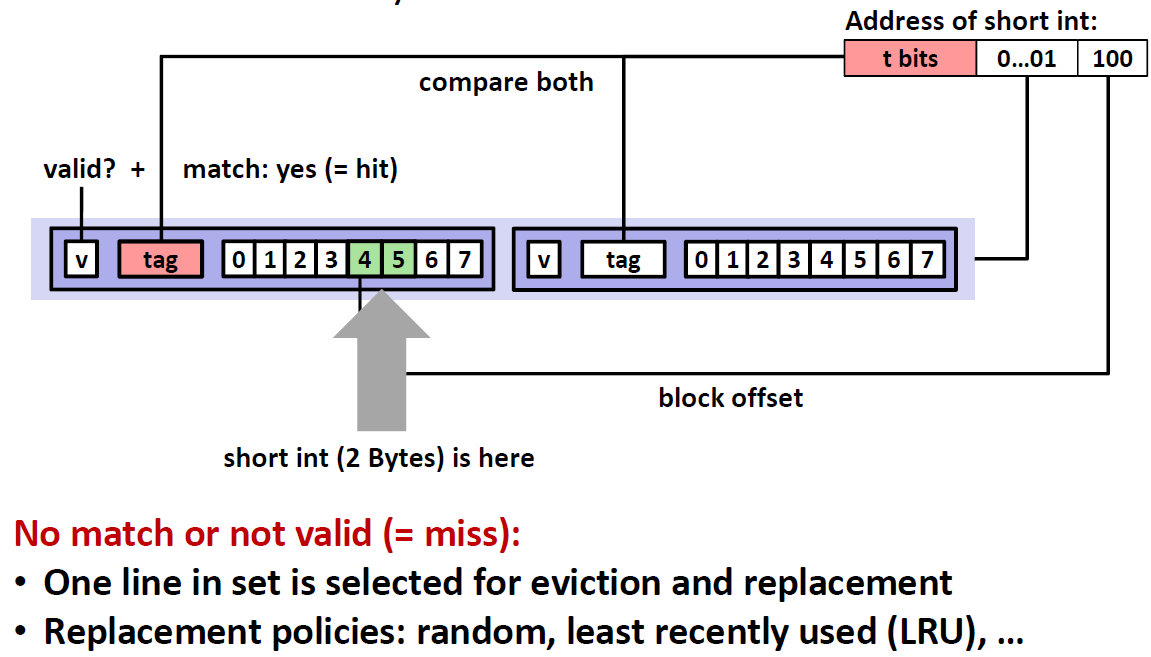
我们用一个例子来模拟E=2时,cache的查找情况:
- 第一个 $[0000_2]$ 肯定是miss的,因为这时候cache里面还没有东西。因此,我们把set0中的cache line1存放 $[0000_2]$ 指向的数据$ M[0-1]$
- 第二行 $[0001_2]$ ,先匹配set0,然后匹配tag 00,匹配成功,于是 hit
- 第三行 $[0111_2]$ ,先匹配set1,然后匹配tag 01,发现cache line是空的,所以miss
- 第四行 $[1000_2]$ ,先匹配 set0,然后匹配tag10,发现cache line 是空的,所以miss
- 第五行 $[0000_2]$ ,先匹配 set0, 然后匹配set0,发现cache line 非空,所以hit
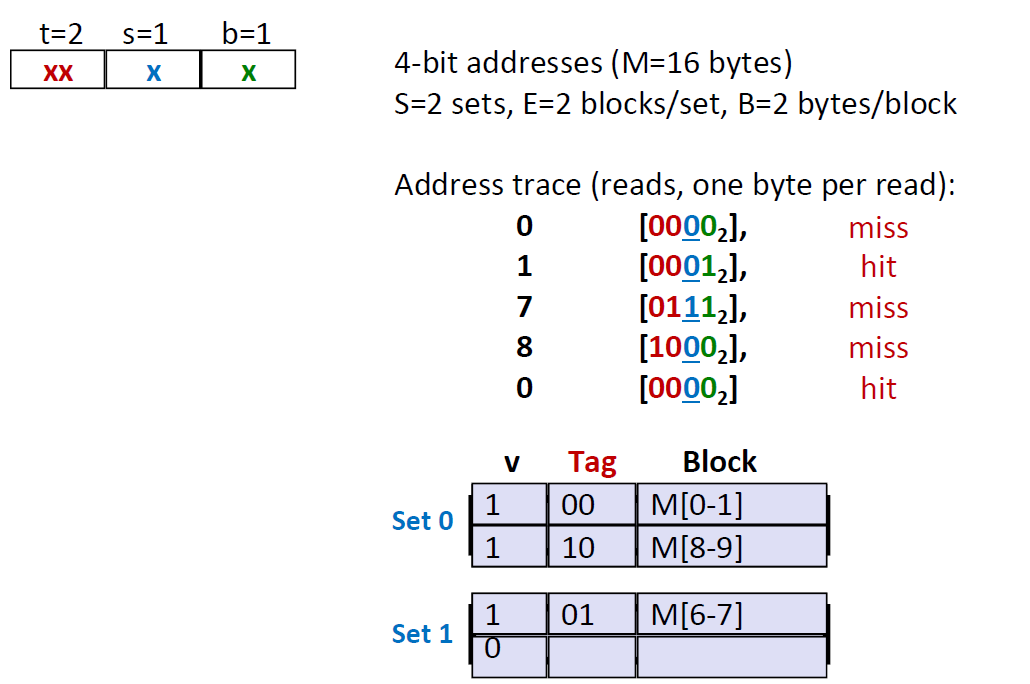
我们看到,读取同样的数据,因为我们的分配方式不同。两路的组相连cache 比 直接写入内存(E=1)少了一次 miss,多了一次hit,因此更加灵活。
小问题
一个地址,为什么要把tag设为前面几位,而把set设置在中间几位呢?
如果把 前面几位设置成set的话,会导致以下这种结果。
set0会在最前面,set1第二……,每一个set中间又是连续的。这样我在一段地址里面进行读写循环,会导致conflict miss的几率大大提高,严重降低机器的运行效率

而将Tag放在前面,将set放在中间,那么在一块连续的内存当中,相同set的地址不会挤在一起,从而降低了conflict miss,并提高了机器的运行效率

现在我们来做一个小练习:假想一个高速缓存,用地址的高s 位做组索引,那么内存块连续的片(chunk)会被映射到同一个高速缓存组。
A. 每个这样的连续的数组片中有多少个块
B. 考虑下面的代码,它运行在一个高速缓存形式为$(S,E,B,m) = (512,1,32,32)$ 的系统上
1 | int array[40960; |
我们首先要知道如果用地址的高s位作为组索引,整个地址的三部分结构如下:
那么随着地址的渐渐增加,我们址答每个连续的数组片(chunk) 是由$2^t$个块组成的,这里t是标记位数。因此,数组头$2^t$ 个块都会映射到组0,而接下来$2^t$ 个块 会被映射到组1,以此类推
对于B小题来说,我们可以轻易地计算出s = 9,b = 5,因此t=32-14=18位,也就是说数组中头 $2^{18}$ 个块会被映射到组0。现在我们来计算数组需要占用多少块。我们的数组只由$(4096*4)/32 =512$ 个块组成,所以数组中所有的块都会被映射到组0。因此在任何时刻高速缓存至多只能保存一个数组块。很明显用高位做索引不能充分利用cache
Cache Write
刚才我们讨论了 cache 的读取,现在我们来讨论一下cache的写入。
Write-Hit
如果我们要写入的数据在cache line中,这时候叫做cache hit 当我们这时候我们要做一个选择:
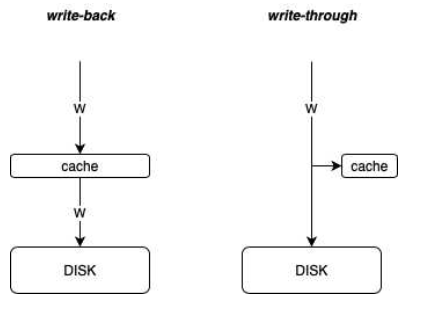
- 通写 write-through(write immediately to memory)
数据被立即写入磁盘,另外也会在缓存保存一份(用来提升读性能)。
- 回写 write-back(defer write to memory until replacement of line)
先写到cache line里, 用回写这种机制的时候,需要在cache line 中添加一个dirty bit(脏位),这个dirty就代表这行cache line暂时还没有写到磁盘当中去,所以我们在找victim的时候,当我们发现这个cache line 是干净的,那么就直接将其替换即可,如果这行cache line是脏的, 在这时候就要将cache line中的数据存到内存中去。
这两者的差别也可以用图表示出来:
回写的优点:
write-back:磁盘写性能高,每次只要写一行cache line 即可
回写的缺点:
wirite-back:系统崩溃或突然断电时,cache中的数据会丢失。有时候另外一个线程在读取数据的时候,可能会导致读取的和写入的不一致。
通写的优点:
读取和写入永远是一致的
通写的缺点:
开销很大
Write-miss
如果我们要写入的数据没有存放在 cache line当中,那么这时候就是 Write-miss
比如说我在键盘中输入的数据,肯定是cache line中没有的,根据计算机硬件架构体系,这些数据首先会被存入到内存当中。
- 写分配 Write-allocate (将要写入的数据从内存中取出放到cache当中并更新cache line)
- 非写分配 No-write-allocate (直接写到memory当中,不更新cache)
目前的系统常用的机制是 :write-back + write-allocate
Cache Performance Metrics
Miss rate
Miss rate = 1- Hit rate ,因为一次访问存取要么miss 要么 hit
一般情况下, L1 cache 的miss rate是 3%-10%
L2 cache 的miss rate 一般在 1% 以下。
Hit Time
Hit Time即当我命中cache 和从cache 中取到数所花费的时间,包括了查找set,匹配tag的时间
比较典型的例子:
对于L1 cache 来说,是4个运行周期
对于L2 cache 来说,是10个运行周期
Miss Penalty
当我们出现 miss的情况,需要大概50-200个运行周期去从内存中取得我们的数据。
问题:为什么不用hit rate 而用 miss rate?
因为用户更关心的是平均访问的时间,对于hit rate来说,其值一般在90%以上,那么当hit rate 相差 1% 的时候,比如从97%提升到99%,看上去这两个数相差了2%,以为提升的幅度很小;而事实上miss rate却从3%降到了1%,机器的性能提升了不止一倍。假设一共有100次cache 读取,之前是3*200+97*4 而现在变成了 1*200+99*4,相差接近3倍,这是hit rate反映不出来的,而miss rate从3%降至1%则能体现出这种倍数差距。
miss rate在0%-10%所反映的和电脑实际性能之间基本上是呈线性关系的,但是显然 hit rate 并不是线性关系。
The memory mountain 内存山
内存山是整本书最有代表性的
- Read throughput 读的带宽
- 也就是从内存中每秒能读取多少数据
- Memory mountain:我们运行一个能反应空间局部性和时间局部性对读取吞吐量变化的函数,然后将其可视化出来
测试原理如下:
stride是步长,此外,我们还定义了2倍步长,3倍步长和4倍步长. 每一次我们加上1、2、3、4倍步长
data数组总的长度是elems,因为要保证加上4倍步长不能冲出数组,所以循环到 length-sx4这个长度为止
1 | long data[MAXELEMS]; /* Global array to traverse */ |
跑之前先要测试一遍,来把cache 填满,因为cache 之前是空的
acc1,2,3,4每次循环都会被调用,所以他们几乎不会出寄存器,data数组在内存当中,每次访问的是 data[i+xstride],因为data数组是在内存中连续存储的,因此 stride越大,说明空间局部性越弱;stride越小,代表空间局部性越强
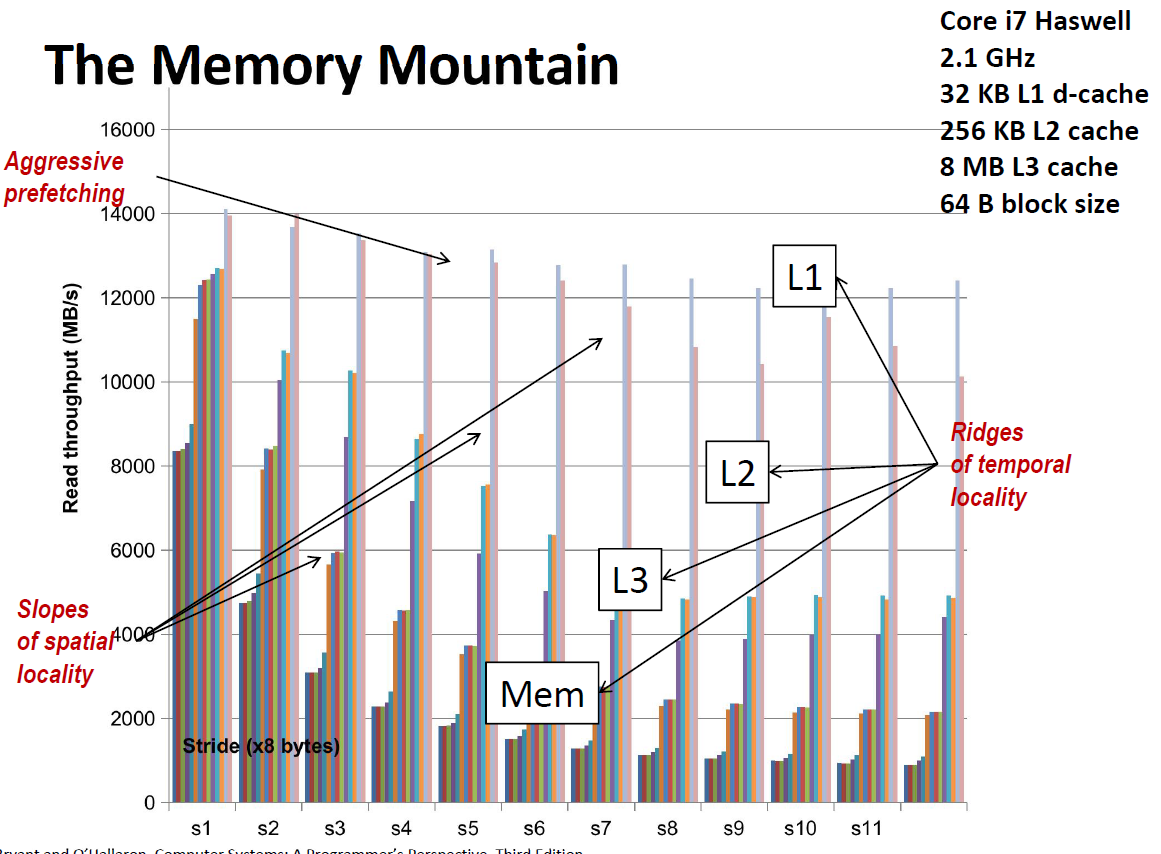
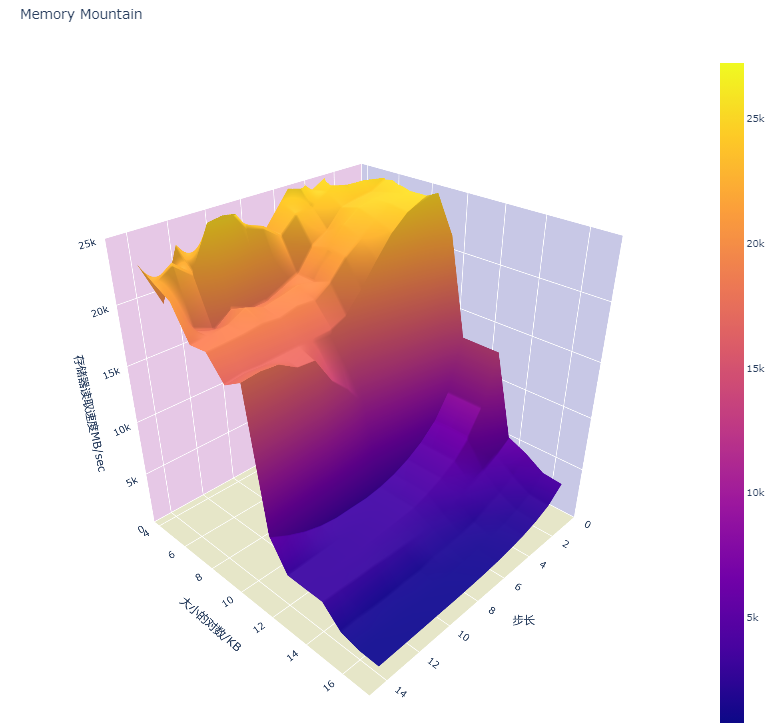
下面是根据吞吐量画出来的内存山:吞吐率越高,性能越好,吞吐率越低,性能越差。
当步长较小的时候,即使是好几倍的步长,也跳不出 L1 cache,因此吞吐量始终维持在一个很高的水平。(黄色部分)
但随着步长的增加,读取的时候会跳出L1 cache,进入L2 cache 或者 L3 cache,这时候吞吐量就下了一个很大的台阶。表现为橙色和紫色部分。
当步长达到一定程度的时候,我们发现吞吐率不会下降了,这是因为每次读取都是cache miss,必须回到内存中去读取,所以速度最慢。表现为深蓝色部分
 ,
,
Rearrangeing loops to improve spatial locality(提升空间复杂度)
我们用矩阵乘法来举例子,最基本的矩阵乘法的写法如下:
1 | /* ijk */ |
数据类型都是long ,也就是8个bytes,算法的复杂度为 $O(N^3)$
现在我们来分析一下 矩阵乘法的miss rate
我们对矩阵和cache提出这些假设:
- Block size = 32B
- 矩阵的边长(N)非常大,1/N 接近于0 (如高分辨率的图片)
- 矩阵大到连cache都放不下一行数据
分析方法
我们对最内层循环进行分析:
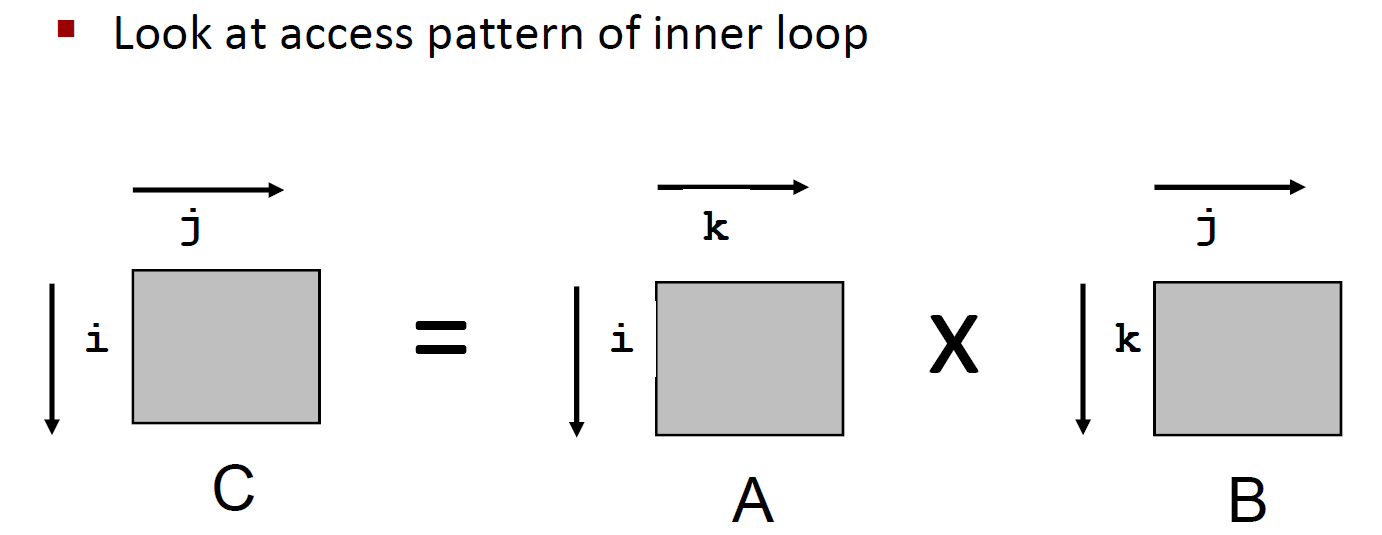
1 | for (i = 0; i < N; i++) |
我们知道,C语言中的数组是按照行存放的。每次循环访问的都是同一行的数字,因此这个循环对于a矩阵的局部性是非常好的。但是因为这个数组的边非常大,cache都放不下,因此还是存在一定的 miss rate。这个miss rate 可以由 $\frac{sizeof(a{ij})}{B}$ 来计算(B指Block的大小),也就是说每访问$ B/ sizeof(a{ij})$ 个数据后,会出现 一次miss。
但是如果稍微改一下算法,虽然不改变最终结果和算法的复杂度,但是也会让局部性变得很差
1 | for (i = 0; i < n; i++) |
比如改成上面这样子,每次跳一行来读取一个数字,因为cache 放不下一行,所以必然每次都会出现miss,因此这个算法的miss rate = 1,局部性非常差
三种不同的矩阵乘法的写法
Matrix Multiplication (ijk)
1 | /* ijk */ |
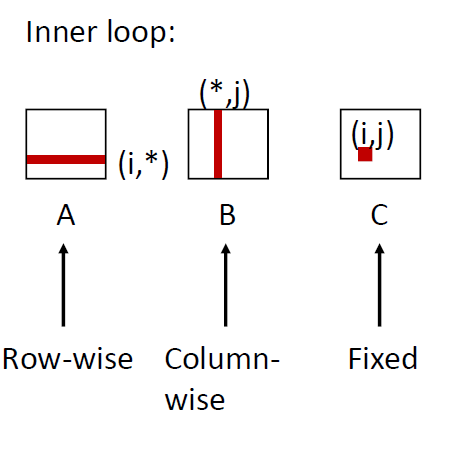
Block = 32B, 数据类型为long
这个miss rate可以这样来计算:
对于A矩阵:每次访问四个数据出现一次miss ,miss rate = 0.25
对于B矩阵:每次都是跳了一行,因此 miss rate = 1
对于C矩阵:只要求在指定位置写入即可,miss rate = 0
avg misses/iter = 1.25
Matrix Multiplication (kij)
1 | for (k=0; k<n; k++) { |
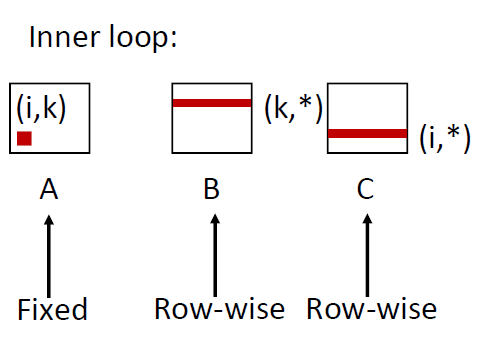
这个矩阵乘法比较奇怪
在最里面的循环,a矩阵并不要进行操作,因此其miss rate = 0
对于B矩阵和C矩阵移动的是j,因此他们的miss rate = 0.25
avg misses/iter = 0.5
Matrix Multiplication (jki)
1 | /* jki */ |
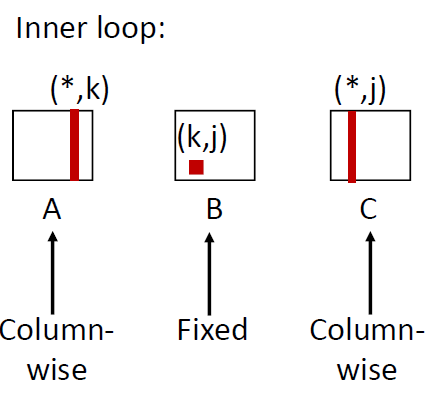
这种算法的局部性最差,A矩阵和C矩阵都是跳行访问的,miss rate = 1.0,而B是固定的,miss rate =0
avg misses/iter = 2.0
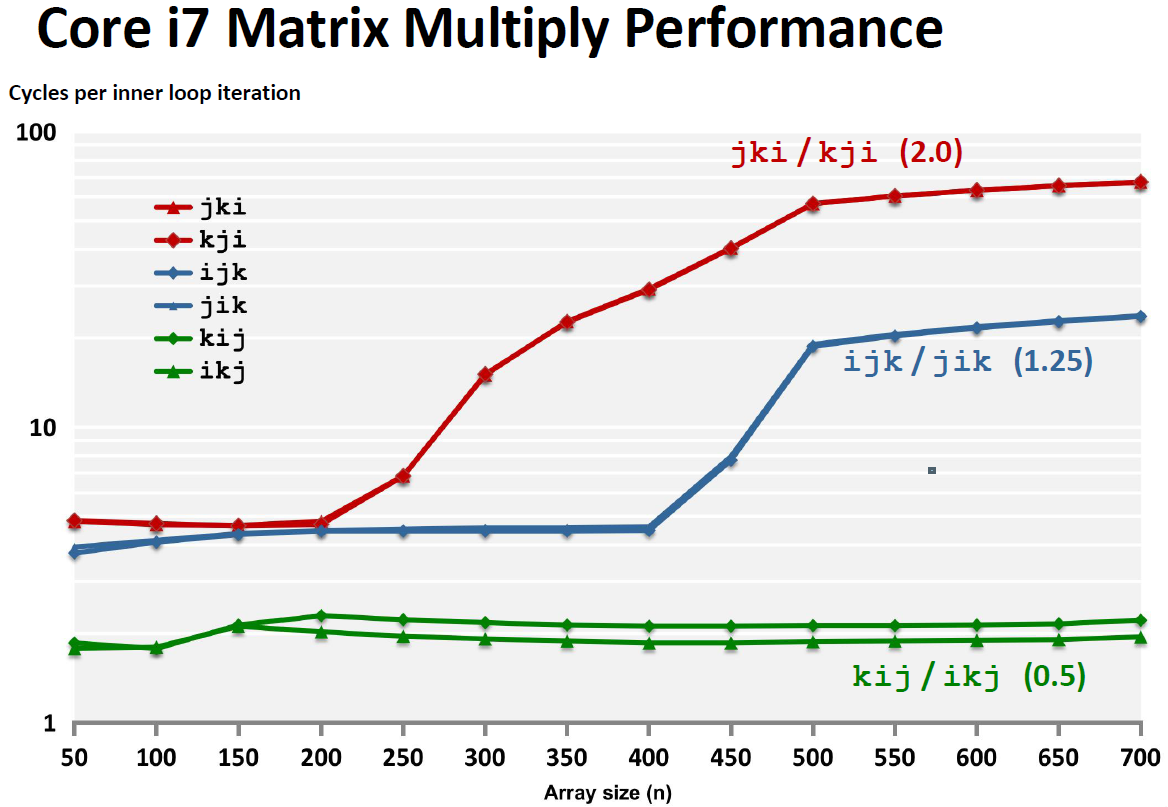
从实验数据上也可以看到这个差别:
Using Blocking to improve temporal locality(时间复杂度)
我们还是拿矩阵乘法来举例
1 | c = (double *) calloc(sizeof(double), n*n); |
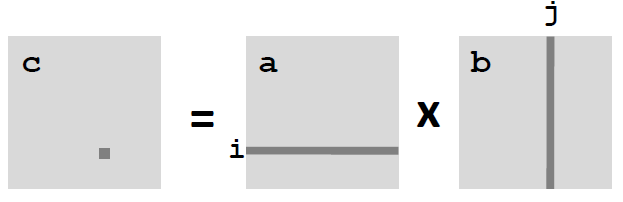
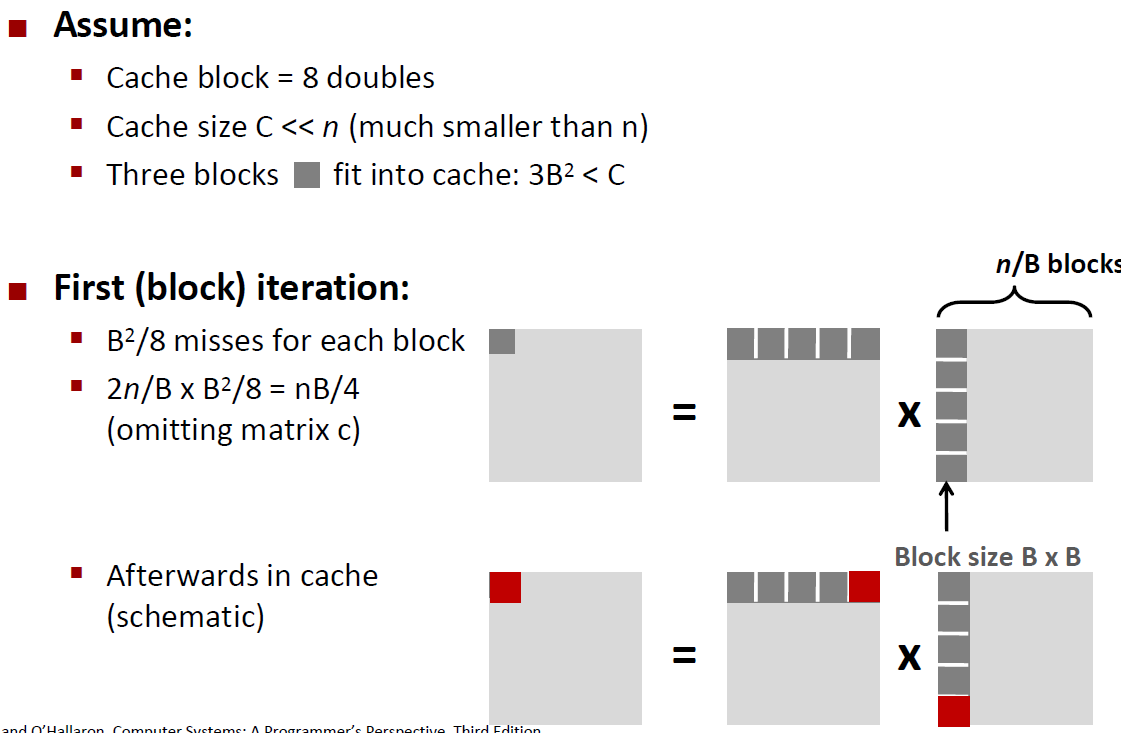
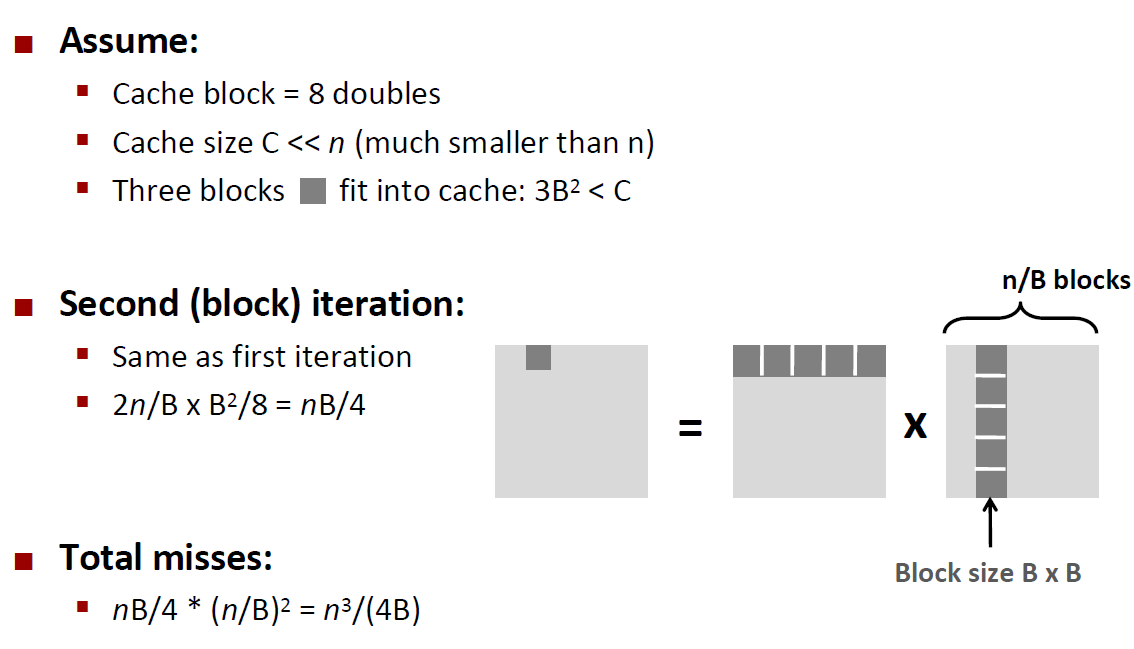
Blocking Summary

练习题
1
下列三个函数,以不同的空间局部性成都,执行相同的操作,请对这些空间函数就空间局部性进行排序。并解释如何得到排序结果
a) structs 数组
1 |
|
b) clear1 函数
1 | void clear1(point *p,int n) |
c) clear2 函数
1 | void clear2(point *p, int n) { |
d) clear 3数组
1 | for (j = 0; j < 3; j++) |
我们知道判断空间局部性的好坏,就要看步长、扫描顺序。首先我们画出struct的结构如下:
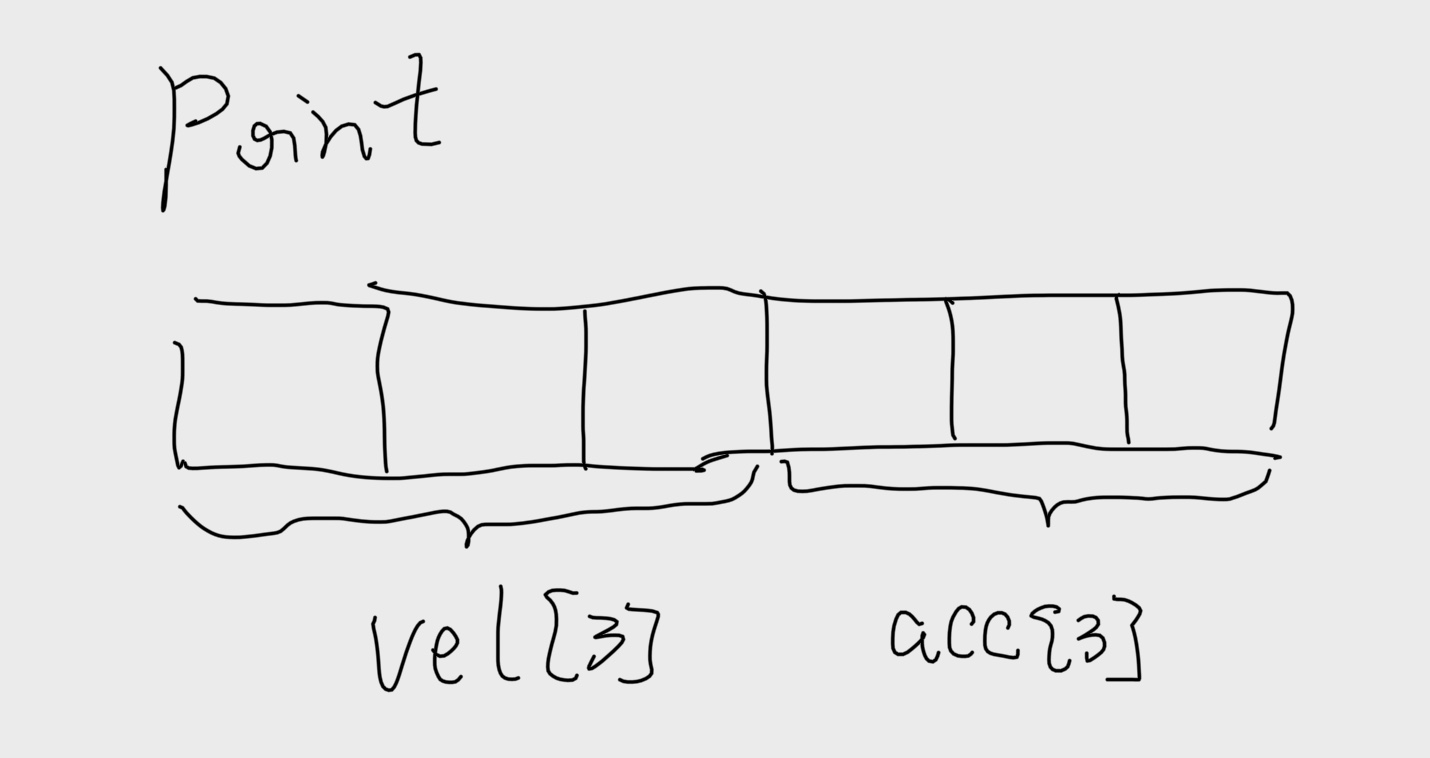
我们先来看看clear1,它以步长为1的引用模式访问vel数组和acc数组,因此明显地具有最好的空间局部性。
clear2和clear1一样,是依次扫描N个结构中的一个,但是在每个结构当中步长并不为1,比如当j = 0的时候,vel[j] 偏移量为0,而acc[j] 的偏移量为12。所以说clear2的空间局部性比clear1要更差一些。
函数clear3不仅在每个结构当中跳来跳去,而且还要从结构跳到结构,所以clear3的空间局部性比clear2和clear1都要差
2
在信号处理和科学计算的应用中,转置矩阵的行和列是一个很重要的问题。从局部性的角度来看,它也很有趣,因为它的引用模式既是以行为主 (wise)的,也是以列为主(column-wise)的。例如,考虑下面的转置函数
1 | typedef int array[2][2]; |
假设在一台具有如下属性的机器上运行这段代码
- sizeof(int) =4
- src数组从地址0开始,dst数组从地址16(十进制)开始
- 只有一个L1告诉数据缓存,他是直接映射的、直写的和写分配的。块的大小为8个字节
- 这个高速缓存总的大小为16个数据字节(16 data bytes),一开始是空的
- 对 src和dst数组的访问分别是读和写不命中的唯一来源
A.对每个row和col,指明对$src[row][col]$和 $dst[row][col]$ 的访问时命中还是不命中。例如,读$src[0][0]$ 会不命中,写$dst[0][0]$ 也不会命中
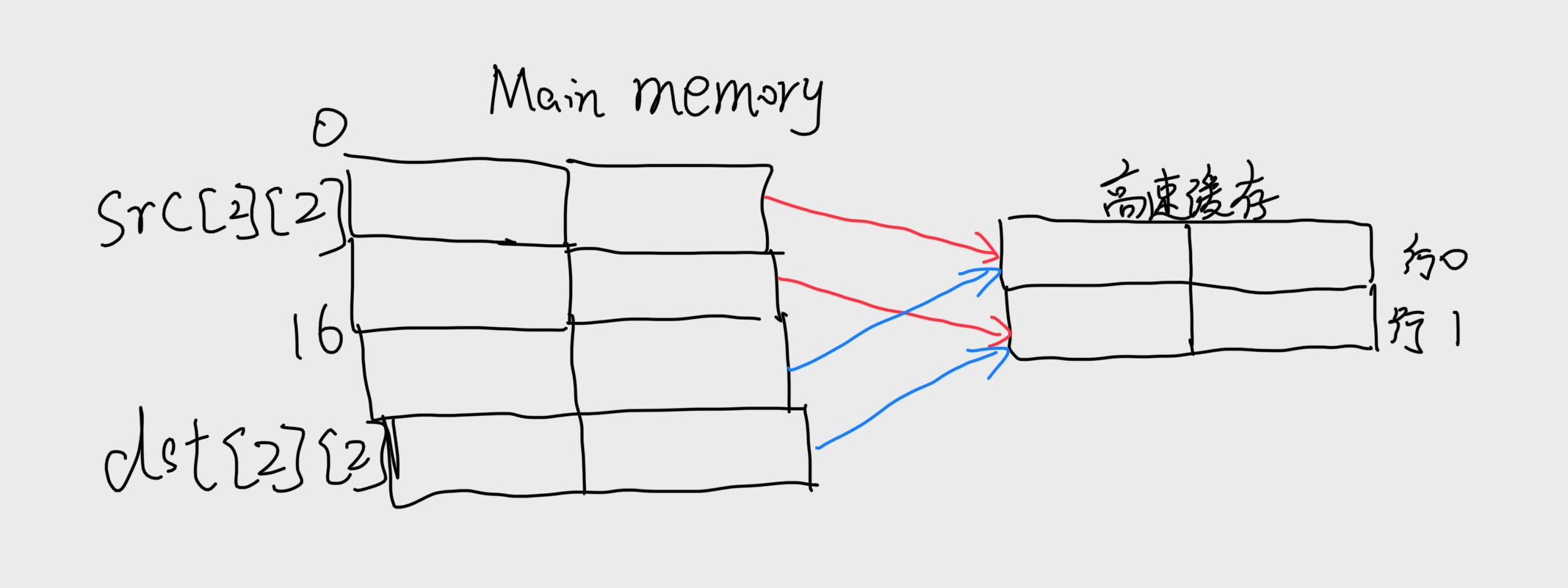
首先我们要画出src和dst的图像,如上图所示。这里注意,每个高速缓存行只包含数组的一个行,杠苏缓存正好只能够保存一个数组。而且对于所有的i,src和dst的行i是映射到同一个高速缓存行的。但是我们发现Cache是肯定不够大的,所以对一个数组的引用总是要驱逐另一个数组的有用的行。
比如说对 $dst[0][0]$ 写会驱逐当我们读 $src[0][0]$ 时加载进来的那一行。所以当我们接下来读取$src[0][1]$ 时,会有一个不命中。
B. 对于一个大小为32数据字节的Cache重复这个练习
当高速缓存为32字节的时候,它足够大,并能容纳这两个数组。因此,所有的不命中都是开始时的冷不命中。
3
最近一个很成功的游戏SimAquarium 的核心就是一个紧密循环(tight loop), 它计算256 个海藻(algae)的平均位置。在一台具有块大小为16 字节(B=16) .整个大小为1024 字节的直接映射数据缓存的机器上测量它的高速缓存性能。定义如下:
1 | struct algae_position { |
还有如下假设:
- sizeof(int) = 4
- grid 从内存地址0开始
- 这个高速缓存开始时是空的
- 唯一的内存访问时对数组grid的元素的访问。变量 i,j,total_x和total_y 存放在寄存器当中
确定下面代码的高速缓存性能:
1 | for (i = 31; i >= 0; i--) { |
首先我们要画出这struct的结构和整一个struct数组的样子
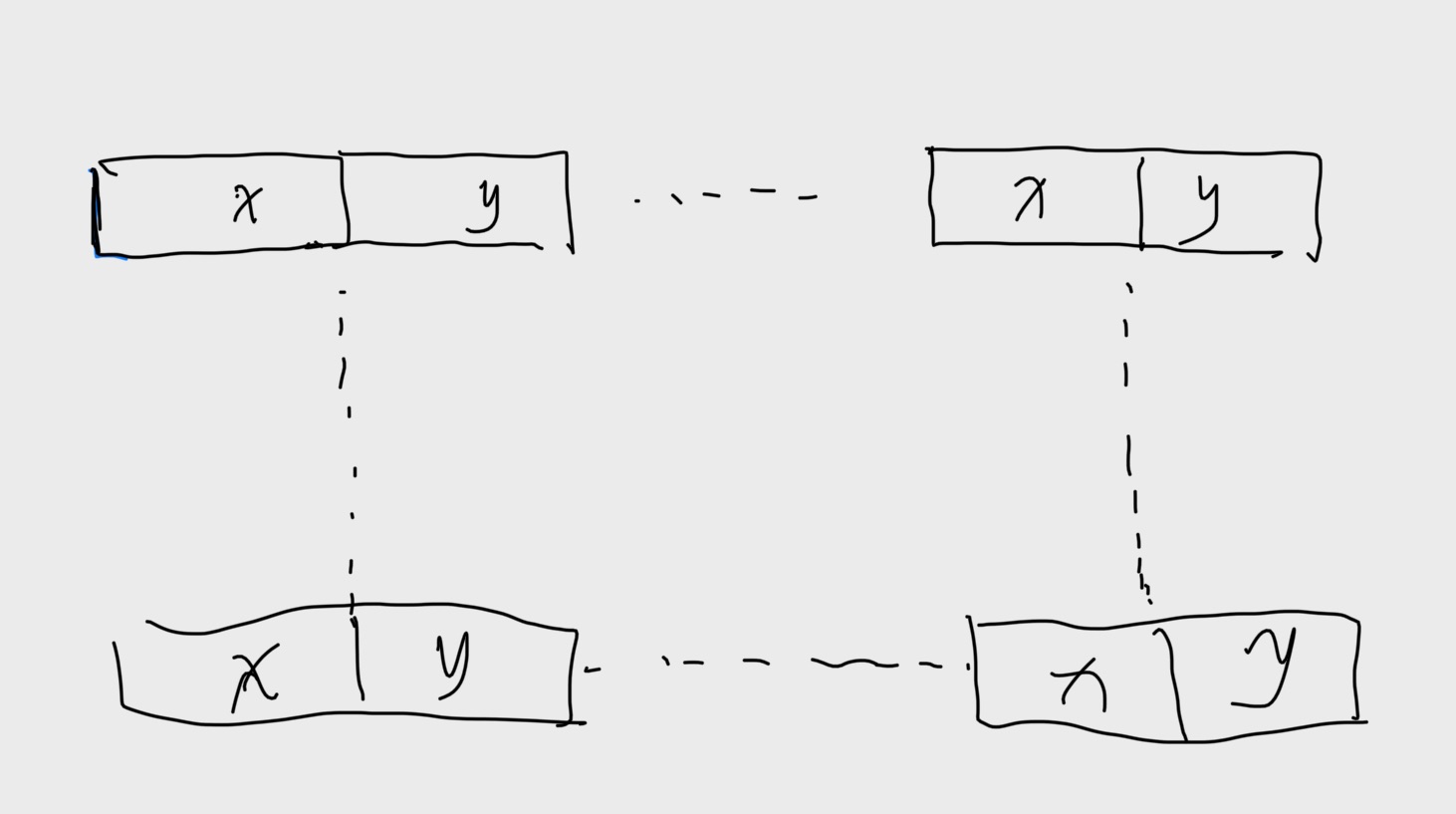
每个16字节的高速缓存包含着两个连续的algae_position 结构。每个循环按照内存的访问顺序访问这些结构,每次读一个整数元素。所以每个循环的模式就是不命中、命中、不命中、命中,依次类推。这里我们不必实际列举出读和不命中的总数就能预测出不命中率为50%
A. 读总数是多少?
读的总数为 16*16 = 256
B. 缓存不命中的读总数是多少?
缓存不命中的总数是256
C. 不命中率是多少? 50%
4
给定上面的四条假设
- sizeof(int) = 4
- grid 从内存地址0开始
- 这个高速缓存开始时是空的
- 唯一的内存访问时对数组grid的元素的访问。变量 i,j,total_x和total_y 存放在寄存器当中
确定下列代码的高速缓存性
1 | for (i = 0; i < 16; i++){ |
A. 读总数是多少?512
B. 高速缓存不命中的读总数是多少? 256
如图所示:
C. 不命中率是多少?50%
D. 如果高速缓存有两倍大,那么不命中率会是多少呢?如果高速缓存有现在的两倍大,那么它能保存整个grid数组。所有的不命中都会是开始时的冷不命中,而不命中的概率会降低到25%
确定下面代码的高速缓存性能
1 | for (i = 0; i < 16; i++){ |
这个循环有很好的步长为1的引用模式,因此所有的不命中都是最开始时的冷不命中。
A. 读总数是多少?512
B. 高速缓存不命中的读总数是多少? 128
C. 不命中率是多少? 25%
D.如果高速缓存有两倍大,那么不命中率会是多少呢?无论高速缓存的大小增加多少,还是会冷命中,因此不会改变不命中率,因为冷不命中时不可能避免的。
5
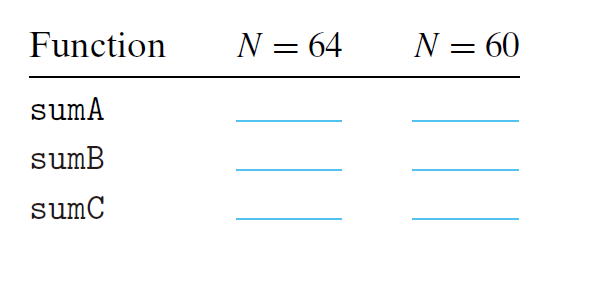
假设我们再下列条件下执行代码中的三个求和函数
- sizeof(int) = 4
- 机器有4KB直接映射的高速缓存,块大小为16字节
- 在两个循环中,代码只对数据进行内存访问。循环索引和值sum都存放在寄存器当中
- 数组a从内存地址 0x8000000处开始存储
对于N=64和N=60 这两种情况,在表中填写他们大概的高速缓存不命中率

当N=64的时候首先我们要画出cache的草图和数组的草图
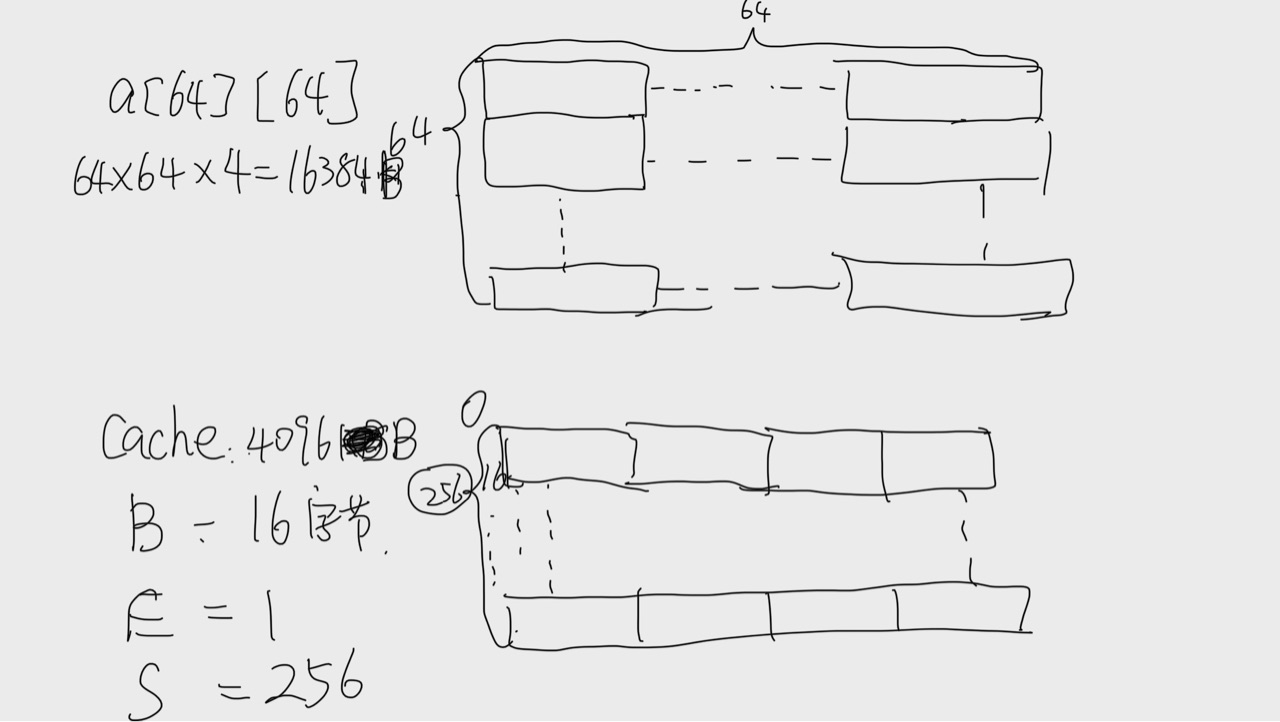
因为数组的大小为cache的4倍,而cache又是直接映射的缓存,所以每次存储255个block就要从头开始,一共四次。所以对于前1/4个数组,出现的是cold miss,而且miss一次会hit3次。后面3/4个数组出现的是conflict miss,但也是miss一次hit3次。因此 miss rate = 25%

对于 sumB,它的局部性是比较差的,read cache order如下:
我们是按照 $a[0][0],a[1][0],a[2][0]$这样的顺序访问的,每次跳一行,一行64*4=256个字节,也就是会跳16个block,因此一开始的时候我们是读取第 $0,16,32…240$ 个cache的,但是这样还只到$a[15][0]$ 当读取$a[16][0]$ 的时候又会返回到第0个cache
0,16,32…240(4times);1,17,33,…241,(4 times)…;15,31,47,…255 (4 times)
对于 sumC
1 | for (i = 0; i < N; i+=2) |
如果读取了$a[j][i],a[j+1][i]$ 那么 $a[j][i+1],a[j+1][i+1]$肯定是hit的
因此我们可以简化成
1 | for (i = 0; i < N; i+=2) |
上面这个函数和下面这个函数是等价的。
1 | for (i = 0; i < N; i+=2) |
这和sumB类似,但是因为$i+=2$,所以read cache order只做了2次循环
因此对于这个函数,missrate = 50%,但同时,对于原函数miss count = $64/26450\% $ = 64*64/4
所以missrate仍然是25%
如果 N=60 的话,那么 对于 sumA和sumC都和 N=64是一样的,为25%
let’s see first inner loop $a[0][0] -> a[59][0]$
read memory address order:
0, 60*4, 60*4*2, …. 60*4*59
read cache order:
0, 15, 30, …., 225, (17 numbers) 255, 14, 29, ….., 224, (17 numbers) 254, 13, 28, ….., 223, (17 numbers) 253, 12, 27, 42, 57, 72, 87, 102, 117 (9 numbers)
all read miss and store into different blocks
next 3 loops: $a[0][1] -> a[59][1], a[0][2] -> a[59][2], a[0][3] -> a[59][3]$
all hit
althrough N is smaller and not power of 2, miss rate is still 25%