最长公共/上升子序列
什么是LCS
现在我们拿到2个字符串
string1:a b c d e f g h i
string 2 : c d g i
我们发现,string1中的子序列 c d g i 和string2 的子序列 c d g i(也就是string2本身)相匹配,且下标是严格递增的那么我们说这两个字符串的最长公共子序列是:\
但是下面这种情况,最长字串还是 \
string1: a b c d e f g h i
string2 :e c d g i
虽然 string1和string2中都有e,但是因为他们的下标并不是严格递增的,因此 e c g d i 并不是string1和string2 的子序列。
最后一个例子:
string1: a b d a c e
string2: b a b c e
这里,我们发现 \ 和 \ 都是string1和string2的最长公共子串,因此,LCS的个数是不唯一的
通过上面这些例子,我们可以这样来解释最长公共子序列问题(longest common subsequence problem):
给定两个序列 $X=
LCS using recursion
现在我们来讨论一下LCS的子问题,对两个序列 $X=
- 如果 $xm=y_n$,则我们应该求解 $X{m-1}$ 和 $Y_{n-1}$ 的一个LCS。并将 $x_m=y_n$ 追加到这个LCS的末尾,也就得到了 X和Y的一个LCS
- 如果$xm\neq y_n$ 那么我们必须求解两个子问题: 求 $X{m-1}$ 和 $Y$ 的一个 LCS 与 $X$ 和 $Y_{n-1}$ 的一个LCS。两个LCS的较长者(或者一样长)即为X和Y的一个LCS。
上述子问题包括了所有情况,我们可以像矩阵链乘法一样写一个最优解的递归式。我们定义 $c[i,j]$ 表示 $X_i$ 和 $Y_j$ 的LCS长度,如果i =0 或者j=0,即一个序列的长度就等于0,那么LCS的长度为0。公式如下:
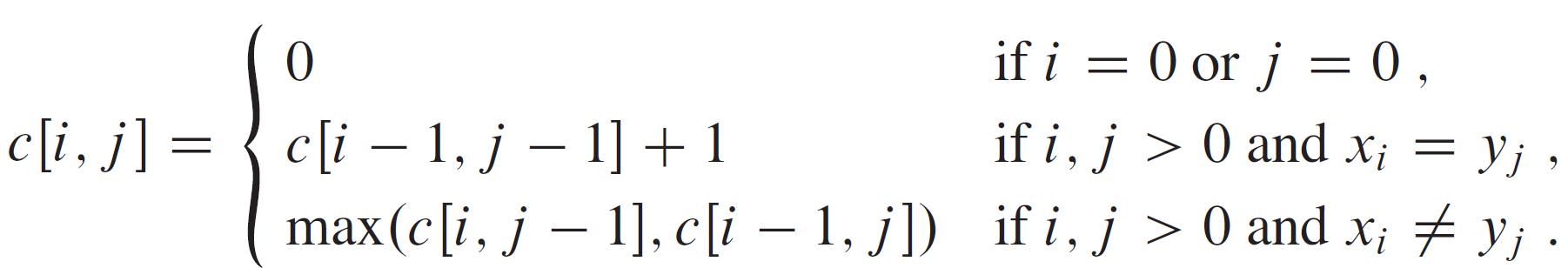
我们用一个例子来展现一个简单的递归过程

LCS using memoisation
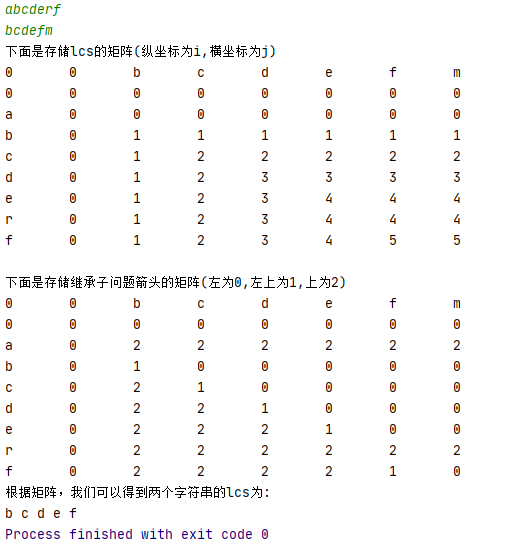
我们可以用一个二维数组记录下子问题的最优解。当$i,j$ 等于0的时候,其所在的那一行就填写0。剩下的格子中的数值取决于它左边上面的最大值(当$x_i\neq y_j$) 的时候,或者其左上方的格子+1(当$x_i = y_j$) 的时候。
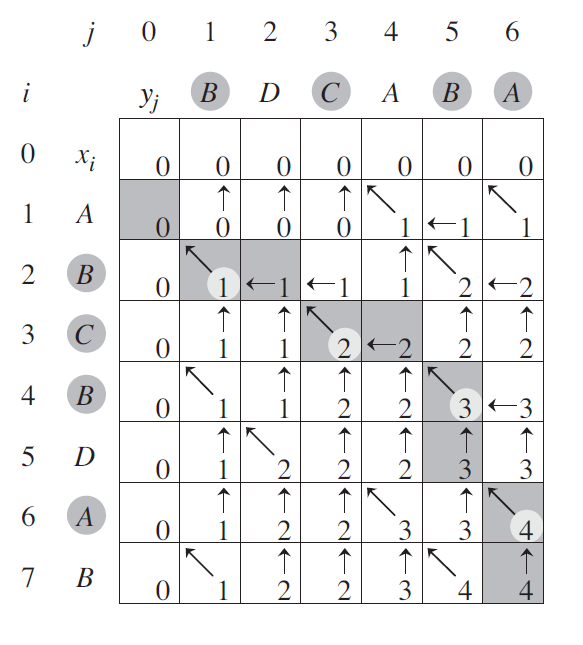
这个算法的时间复杂度即为扫描这个二维数组的时间,设 n=string1.length , m=string2.length ,则 时间复杂度为 $O(mn)$
空间复杂度即为一些常量的存储和二维数组的开销,为$O(mn)+O(1)=O(mn)$
代码
伪代码:


1 |
|